Бабайцев В.А.,Браилов А.В.,Винюков И.А.,Рябов П.Е. Учебник по Высшей математике
Подождите немного. Документ загружается.

ФИНАНСОВАЯ АКАДЕМИЯ
ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра математики и финансовых приложений
В.А. Бабайцев, А.В.Браилов,
И.А.Винюков, П.Е.Рябов
МАТЕМАТИКА ДЛЯ
ЭКОНОМИСТОВ
Руководство к решению задач
Интегральное исчисление
Москва 2003
Рецензенты:
д.физ.-мат. н., проф. А.Г. Попов (МГУ)
проф. В.Н. Салин (ФА)
Бабайцев В.А., Браилов А.В., Винюков И.А., Рябов П.Е. Математика для
экономистов: Руководство к решению задач: Интегральное исчисление. М.: Финансовая
академия, 2003. 96 с.
Данное пособие представляет собой переработку 6-й и 7-й глав "Сборника задач по курсу математики" издания 2001 г. В него
внесены изменения и дополнения в соответствии с новым Госстандартом по математике для общеэкономических специальностей.
В частности, введены параграф "Несобственные интегралы" и глава "Кратные интегралы". Пособие дополнено новыми примерами
и упражнениями, существенно расширен круг рассмотренных примеров, добавлены новые теоретические вопросы.
Руководство предназначено в первую очередь для организации самостоятельной работы студентов по курсу
"Математика" во II семестре 1-го курса.
ISBN 5-7942-0310-2 © Бабайцев В.А.
© Браилов А.В.
© Винюков И.В.
© Рябов П.Е.
© Финансовая академия
при Правительстве РФ, 2003

Глава 1
Неопределенный интеграл
Определение первообразной и неопределенного интеграла
Функцию F(x) называют первообразной для функции f(x), если выполняется равенство F'(x) = f(x).
Совокупность всех первообразных данной функции f(x) называют неопределенным интегралом от функции
f(x) и обозначают символом
. Таким образом,
()
∫
dxxf
()
(
)
∫
+
=
CxFdxxf , если F'(x) = f(x),
где
C − произвольная константа.
Для
непрерывной функции f(x) всегда существует первообразная, следовательно, и неопределенный
интеграл.
Свойства неопределенного интеграла
() ()
∫
+= CxFxdF ;
() ()
;CxFdxxF +=
′
∫
(
)
(
)
(
)
dxxfdxxfd
=
∫
.
() ()
[]
() ()
∫∫∫
+=+ dxxfdxxfdxxfxf
2121
;
() ()
∫∫
= dxxfCdxxCf .
Таблица интегралов
1.
∫
+
+
=
+
C
n
x
dxx
n
n
1
1
, n ≠ −1;
∫
+= Cx
x
dx
2;
∫
+−= C
xx
dx 1
2
.
2.
∫
+= Cx
x
dx
ln .
3.
∫
+= C
a
a
dxa
x
x
ln
,
; . 1≠a
∫
+= Cedxe
xx
4. .
∫
+= Cxxdx sincos
5.
∫
+
−= Cxxdx cossin .
6.
∫
+= Cx
x
dx
tg
cos
2
.
7.
∫
+−= Cx
x
dx
ctg
sin
2
.
8.
∫
+=
−
C
a
x
xa
dx
arcsin
22
;
∫
+=
−
Cx
x
dx
arcsin
1
2
.
9.
∫
+=
+
C
a
x
axa
dx
arctg
1
22
;
∫
+=
+
Cx
x
dx
arctg
1
2
.
10.
∫
+
+
−
=
−
C
ax
ax
aax
dx
ln
2
1
22
.
11.
∫
+±+=
±
Caxx
ax
dx
22
22
ln .

Замечание 1. Любая из написанных формул сохраняет силу и при замене переменной x на
произвольную непрерывно дифференцируемую функцию u(x). Например,
∫
+= Cu
u
du
ln .
Для определения вида функции по заданному виду ее дифференциала применяют различные приемы
интегрирования, которые позволяют решить эту задачу для отдельных классов функций. Ниже приведены
наиболее важные из них.
Замечание 2. Надо иметь в виду, что в общем случае задача выражения первообразной через
элементарные функции не имеет решения. Так, например, не являются элементарными функциями
неопределенные интегралы следующих видов:
∫∫ ∫∫∫∫∫∫
−
dxxxdxxdx
x
e
dxxdxe
x
dx
dx
x
x
dx
x
x
x
x
sin;tg;;sin;;
ln
;
cos
;
sin
2
2
как и все сводящиеся к ним.
§ 1.1. Непосредственное интегрирование
Вычисление неопределенного интеграла с помощью таблицы интегралов (с учетом Замечания 1) и
правил интегрирования называют непосредственным интегрированием.
Примеры
1.
∫
+= C
x
dxx
7
7
6
.
2.
∫∫
+=+==
−
C
x
C
x
dxx
x
dx
2
3
3
2
3
2
3
2
3
1
3
.
3.
∫∫
+=
+
=
+
C
x
x
dx
x
dx
2
arctg
2
1
24
222
.
4.
()
∫∫ ∫∫
=+−=+− dxxxdxdxxdxxxx
2
1
33
5sin325sin32
C
xx
x
x
C
x
x
x
+++=+++
3
10
cos3
2
2
3
5cos3
4
2
4
2
3
4
= .
5.
Cxxdxdxx +
+−=
+
+=
+
∫∫
3
cos
33
sin
3
sin
ππππ
.
6.
() ()()()()
∫∫ ∫
=−−=−−=− 6262
2
1
62
2
1
6262
888
xdxxdxdxx
()
(
)
C
x
C
x
+
−
=+
−
18
62
9
62
2
1
99
= .
7.
()
=++=⋅+=+
∫∫ ∫
7272
4
1
472
4
1
72
2222
xdxxdxxdxxx
()
()
C
x
C
x
+
+
=+
+
⋅
6
72
72
4
1
3
2
2
3
2
3
2
= .
8.
()
∫∫ ∫
+==⋅= C
x
xxd
x
dx
xdx
x
x
3
ln
lnlnln
ln
3
22
2
.
9.
()
Cxx
xx
xxd
dx
xx
x
++−=
+−
+−
=
+−
−
∫∫
13ln
13
13
13
32
2
2
2
2
.

10.
() ()
(
)
()
=
−
=
−
=
−
=
−
∫∫ ∫ ∫
2
32
3
2
32
2
2
3
2
6
2
2
3
1
2
3
3
1
4
4
x
xd
x
dxx
x
dxx
x
dxx
C
x
+
2
arcsin
3
1
3
= .
11.
()
∫∫ ∫ ∫
+==⋅=⋅= Cexdexdxexdxedxxe
xxxxx
22222
2
1
2
1
2
2
1
2
.
12.
()
=⋅=
+
⋅=
+
∫∫ ∫
xdx
x
dx
xdx
x
x
arctgarctg
1
arctg
1
arctg
22
()
CxC
x
+=+=
3
2
3
arctg
3
2
2
3
arctg
.
Упражнения
1.1.1.
Дайте определение неопределенного интеграла.
1.1.2. Сформулируйте свойства неопределенного интеграла.
1.1.3. Докажите, что .
()
dxxfdxxfd )()( =
∫
1.1.4. Докажите, что , где − произвольная постоянная. CxFxdF +=
∫
)()( C
1.1.5. Докажите формулу
∫∫∫
+
=
+
dxxgbdxxfadxxbgxaf )()())()((,
где
, b – произвольные числа, не равные нулю одновременно. a
1.1.6. Дайте определение первообразной функции ) на промежутке (xf
X
. Сколько различных
первообразных имеет на нем функция )
? Приведите примеры первообразных для функции
.
(
xf
)1/(1)(
2
xxf +=
1.1.7. Докажите, используя табличное значение интеграла при 1
∫
dxx
n
−
≠
n , что
∫
+
+
+
=+ C
n
bax
a
dxbax
n
n
1
)(1
)(, где
, , C − произвольные постоянные, a . a b 0≠
1.1.8. Докажите, используя табличное значение интеграла
∫
x
dx
, что
∫
++=
+
Cbax
abax
dx
ln
1
, где , ,
− произвольные постоянные,
a .
a b C
0≠
1.1.9. Докажите, что если ) − первообразная для функции ) на промежутке (xF (xf
X
, то все ее
первообразные имеют вид
где − произвольная постоянная. Приведите примеры
первообразных для функции
CxF +)(,
x
axf =)
C
(.
1.1.10. Докажите, что если − первообразная функции ), то выполнено равенство )(xF (xf
∫
+=+ baxF
a
dxbaxf (
1
)(+ C) , где , , C − произвольные постоянные, a . a b 0≠
Найти интегралы, применяя непосредственное интегрирование.
1.1.11.
(
)
(
)
∫
+−+ dxxxx 11.
1.1.12.
∫
+−
dx
x
xexx
x
3
23
.
1.1.13.
∫
+
−
dx
x
a
a
x
x
3
2
1.
1.1.14.
∫
−
−−+
dx
x
xx
4
22
9
33
.
1.1.15.
∫
+
+
dx
x
x
42
115
.
1.1.16.
∫
+
dx
xx
xxxx
cos
cos2sin
3
.
1.1.17. .
()
∫
+ dxxx
2
cossin
1.1.18.
∫
⋅
dx
xx
x
22
cossin
2cos
.
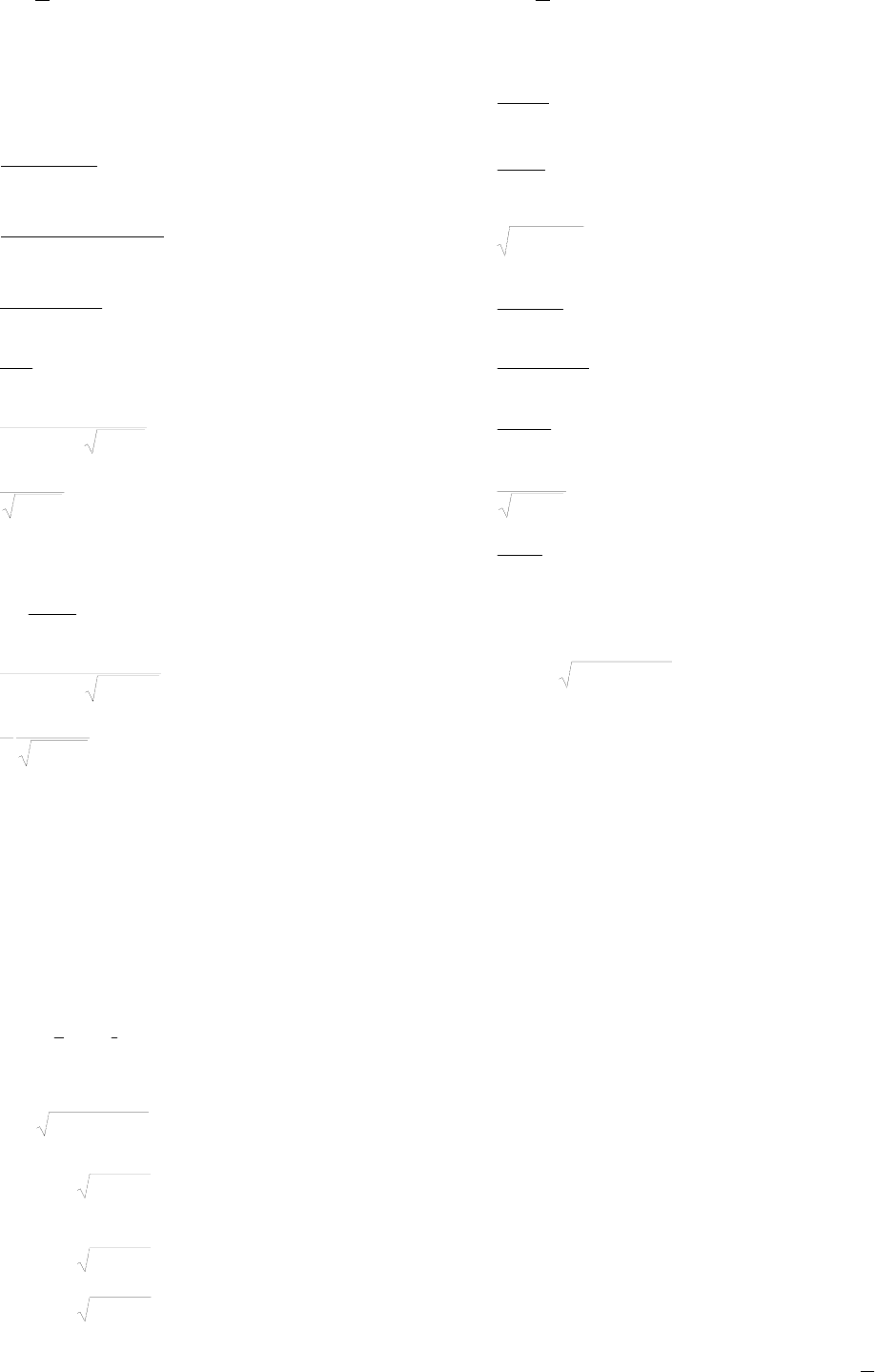
1.1.19.
∫
dx
x
2
sin
2
. 1.1.20.
∫
dx
x
2
cos
2
.
1.1.21. .
∫
xdx
2
ctg 1.1.22. .
∫
xdx
2
tg
1.1.23. .
()
∫
+ dxxx
2
ctgtg
1.1.24.
∫
+
dx
x
x
9
2
4
.
1.1.25.
(
)
∫
+
+
dx
xx
x
22
2
1
21
.
1.1.26.
∫
−
dx
x
2
1
2
.
1.1.27.
(
)
(
)
∫
+++
dx
xxx
x
22
11
.
1.1.28.
()
∫
+ dxx
5
3
72.
1.1.29.
∫
−+
+
dx
xx
x
652
54
2
.
1.1.30.
∫
−
−
−
+
dx
ee
ee
xx
xx
.
1.1.31.
∫
dx
x
xln
. 1.1.32.
∫
⋅
dx
xx
x
cossin
2cos
.
1.1.33.
∫
−⋅
23
1arcsin xx
dx
.
1.1.34.
∫
+
dx
x
x
2
1
arctg
.
1.1.35.
∫
−
dx
x
x
8
3
1
.
1.1.36.
∫
dx
x
x
3
2
cos
sin
.
1.1.37. .
∫
⋅ xdxe
x
sin
cos
1.1.38.
∫
dx
xx ln
1
.
1.1.39.
∫
−
− dx
x
x
2
1
2.
1.1.40.
(
)
∫
−− dxxx
2
11
3
16.
1.1.41.
∫
−
dx
xx І)(1)(arcsinІ
1
.
1.1.42.
∫
+++ dxxxx )1І(3)1(6 .
1.1.43.
∫
+
+
dx
x
x
)3(
49
2
1
.
§ 1.2. Замена переменной в определенном интеграле
Если интеграл нельзя найти непосредственно, то в некоторых случаях можно применить метод замены
переменной, положив
x =
ϕ
(t), где
ϕ
(t) − непрерывно дифференцируемая монотонная функция. Справедлива формула замены
переменной:
(
)
(
)
[
]
(
)
∫∫
′
=
dtttfdxxf
ϕ
ϕ
.
Замечание. Иногда целесообразно применять эту формулу "справа − налево".
Несколько наиболее часто встречающихся замен переменных:
а)
∫
dxxxxR
s
r
n
m
,,, K , где R − рациональная функция своих аргументов. Если k − общий знаменатель
дробей, входящих в показатели степени, то применяют замену переменной x = t
k
.
б)
(
)
∫
++ dxcbxaxxR
2
, сводится после выделения полного квадрата из квадратного трехчлена ax
2
+
bx + c к трем основным видам, к которым можно применить тригонометрические замены переменной:
1)
(
)
∫
− dxxaxR
22
, − замена переменной x = asint или
x = acost.
2)
(
)
∫
+ dxxaxR
22
, − замена переменной x = atgt.
3)
(
)
∫
− dxaxxR
22
, − замена переменной x = asect.
в)
сводится к интегралу от рациональной функции заменой переменной
(
∫
dxxxR cos,sin
)
2
tg
x
t =
(или x = 2arctgt), т.к. имеют место формулы
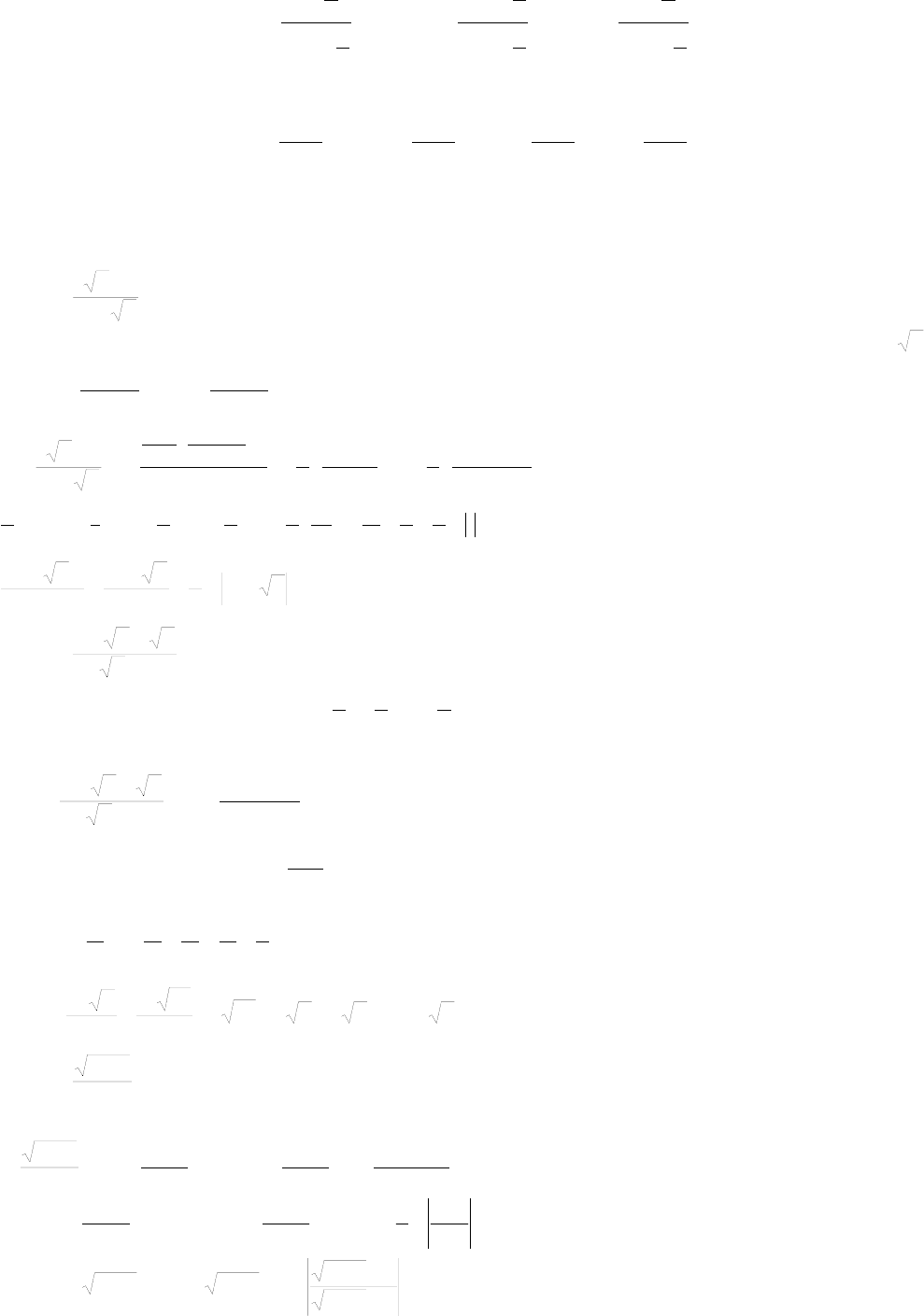
2
tg1
2
tg2
sin
2
x
x
x
+
= ;
2
tg1
2
tg1
cos
2
2
x
x
x
+
−
= ;
2
tg1
2
tg2
tg
2
x
x
x
−
=
или
2
1
2
sin
t
t
x
+
= ;
2
2
1
1
t
t
x
+
−
=
cos
;
2
1
2
tg
t
t
x
−
= ;
2
1
2
t
dt
dx
+
= .
Примеры
1
.
∫
+ x
dxx
21
.
Непосредственно найти этот интеграл нельзя, поэтому применим замену переменной
xt 21+= ;
откуда
()
;
4
1
2
−
=
t
x
()
dt
t
dx
4
12 −
= .
∫
+ x
dxx
21
=
()
∫
−
⋅
−
t
dt
tt
4
12
2
1
=
()
∫
−
dt
t
t
2
1
4
1
=
∫
+−
dt
t
tt 12
4
1
2
=
=
∫
+− dt
t
t
1
2
4
1
=
∫∫∫
+−
t
dt
dttdt
4
1
2
1
4
1
=
Ct
tt
++− ln
4
1
28
2
=
=
()
Cx
xx
+++
+
−
+
21ln
4
1
2
21
8
21
2
.
2.
∫
+
++
dx
x
xx
1
2
6
3
.
Общий знаменатель показателей
,
3
1
6
1
и
2
1
равен 6, следовательно, следует применить замену
.
,
6
tx = dttdx
5
6=
∫
+
++
dx
x
xx
1
2
6
3
∫
=⋅
+
++
= dtt
t
tt
5
32
6
1
2
=
∫
=
+
+−+−+ dt
t
ttttt
1
1
26
2347
()
=+
++−+−+= Ct
ttttt
1ln
2345
2
8
6
3458
()
Cxxxx
xxx
+++−+−+= 1ln12643
5
12
4
3
66
3
2
6
5
3
.
3.
∫
+
dx
x
x 4
.
Применим замену переменной
, откуда ;
2
4 tx =+ 4tdtdx 2
2
−= tx
=
. Тогда
∫
+
dx
x
x 4
=
∫
⋅
−
tdt
t
t
2
4
2
=
∫
− 4
2
2
t
dtt
2
=
∫
−
+−
dt
t
t
4
44
2
2
2
=
=
∫
−
+ dt
t 4
4
12
2
=
∫∫
−
+
4
82
2
t
dt
dt =
C
t
t
t +
+
−
⋅+
2
2
ln
4
1
82
.
Так как
4+= xt , I = C
x
x
x +
++
−+
++
24
24
ln242.
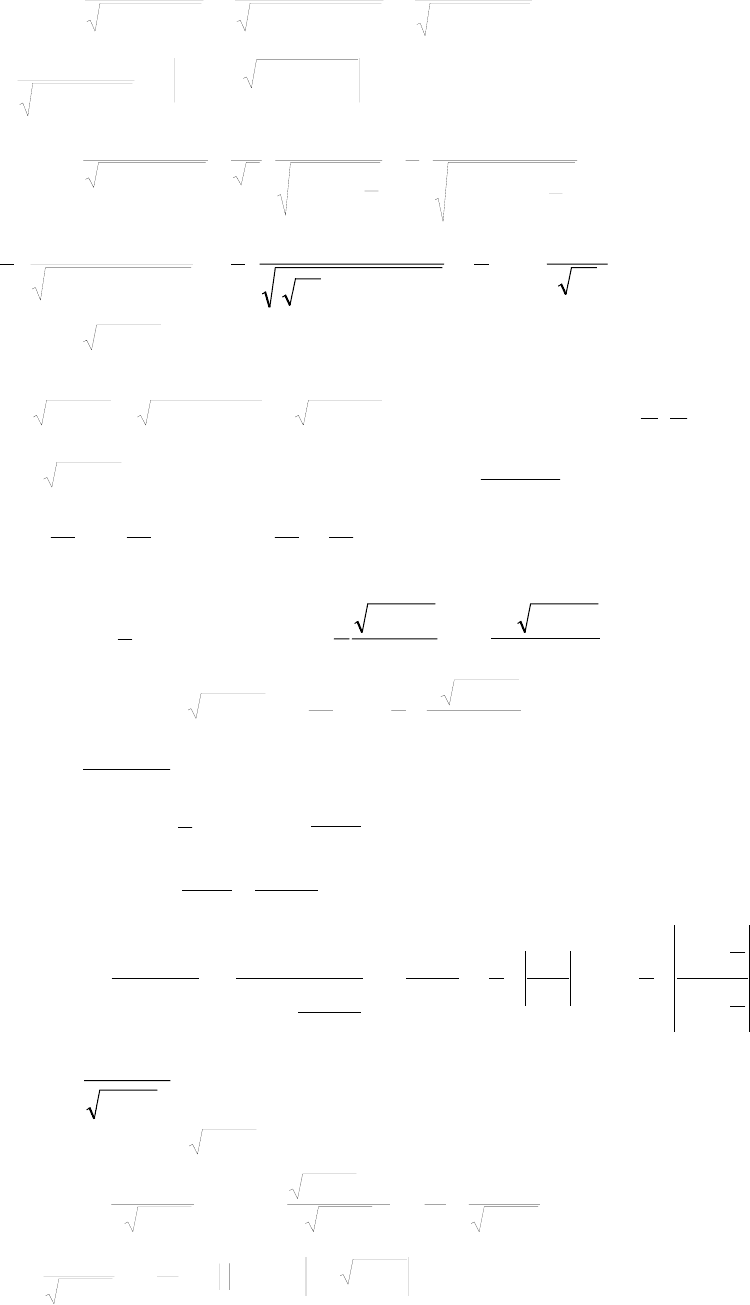
4.
()
∫∫∫
=
−+
=
−++
=
++
12
14434
222
x
dx
xx
dx
xx
dx
=
()
()
Cxxx
x
xd
+++++=
−+
+
∫
342ln
12
2
2
2
.
5.
∫∫∫
=
−−−
=
+−
=
+−
4
5
2
1
4
54
1
544
2
2
2
xx
dx
xx
dx
xx
dx
=
()
∫
+−− 5,15,0
2
1
2
x
dx
=
()
()
()
∫
=
−−
−
2
2
5,05,1
25,0
2
1
x
xd
C
x
+
−
5,1
5,0
arcsin
2
1
.
6.
∫
− dxx
2
25 .
Положим x = 5sint, dx = 5costdt;
=−
2
25 x ttt cos5sin15sin2525
22
=−=− на промежутке
−
2
;
2
ππ
.
∫
− dxx
2
25
∫∫∫
+
==⋅= dt
t
tdttdtt
2
2cos1
25cos25cos5cos5
2
=
∫∫
=+= tdtdt 2cos
2
25
2
25
Ctt ++= 2sin
4
25
2
25
.
Осталось вернуться к переменной x:
5
arcsin
x
t = ; sin2t = 2sintcost =
=
−
5
25
5
2
2
xx
. =
25
252
2
xx −
.
Окончательно,
C
xxx
dxx +
−
+=−
∫
2
25
5
arcsin
2
25
25
2
2
.
7.
∫
+ x
dx
cos53
.
Положим
2
tg
x
t = , тогда
,
1
2
2
t
dt
dx
+
=
2
2
2
2
1
28
1
1
53cos53
t
t
t
t
x
+
−
=
+
−
+=+ .
∫
+ x
dx
cos53
=
()
∫
=
+
−
+
2
2
2
1
28
1
2
t
t
t
dt
∫
−
2
4 t
dt
C
t
t
+
−
+
=
2
2
ln
4
1
C
x
x
+
−
+
=
2
tg2
2
tg2
ln
4
1
.
8.
∫
+ 9
2
x
dx
.
Положим
9
2
++= xxt , тогда
dx
x
x
dt
+
+=
92
2
1
2
;
9
;
9
9
22
2
+
=
+
++
=
x
dx
t
dt
dx
x
xx
dt .
∫
+ 9
2
x
dx
=
CxxCt
t
dt
+++=+=
∫
9lnln
2
.

Упражнения
Найти интегралы, применяя метод замены переменной:
1.2.1.
∫
dx
x
x
2
sin
.
1.2.2.
(
)
∫
dx
x
xlncos
.
1.2.3.
∫
+⋅ dxxx
3
32
31.
1.2.4.
∫
+ 32
3
x
xdx
.
1.2.5. .
∫
xdx
3
cos
1.2.6. dx
x
x
∫
+
4
3
14
3
.
1.2.7.
∫
++
dx
x
x
11
.
1.2.8.
∫
−
dx
x
x
1
4
.
1.2.9. .
∫
xdx
5
cos 1.2.10. .
∫
xdxx
43
cossin
1.2.11. .
∫
xdx
4
tg
1.2.12.
∫
xx
dx
3
cossin
.
1.2.13.
∫
− dxx
2
4.
1.2.14.
∫
−
2
2
1 x
dxx
.
1.2.15.
∫
+
2
1 xx
dx
.
1.2.16.
∫
+1
x
e
dx
.
1.2.17. .
∫
xdx
7
cos 1.2.18.
∫
xdx
5
sin
1.2.19. Выведите формулу замены переменной в неопределенном интеграле. Приведите пример.
§ 1.3. Интегрирование по частям
Метод интегрирования по частям применяют в тех случаях, когда подынтегральная функция
представляется в виде произведения двух функций u и v, из которых хотя бы одна является
трансцендентной (тригонометрическая, обратная тригонометрическая, показательная, логарифмическая,).
Тогда, записывая подынтегральное выражение как произведение функции u на дифференциал другой
функции dv, используем формулу интегрирования по частям
∫∫
−
=
vduuvudv .
Интеграл в правой части формулы может оказаться проще, чем исходный. Например, как в следующих
случаях:
()
∫
xdxxR ln u = lnx, dv = R(x)dx;
()
dxxxR
∫
arctg u = arctgx, dv = R(x)dx;
()
∫
dxexR
x
u = R(x), dv = e
x
dx;
()
∫
xdxxR sin u = R(x), dv = sinxdx;
()
∫
xdxdxxR cos u = R(x), dv = cosxdx,
где R(x) − рациональная функция (в частности, многочлен).
Примеры
1
. =
+
−=
+
−=
∫∫∫
22
1
2
2
1
arctg
1
arctgarctg
x
xdx
xxdx
x
x
xxxdx
u = arctgx
2
1 x
dx
du
+
=
dv = dx
∫
== xdxv (положим C = 0)
= xarctgx −
()
∫
+
+
2
2
1
1
2
1
x
xd
= xarctgx −
()
Cx ++
2
1ln
2
1
.
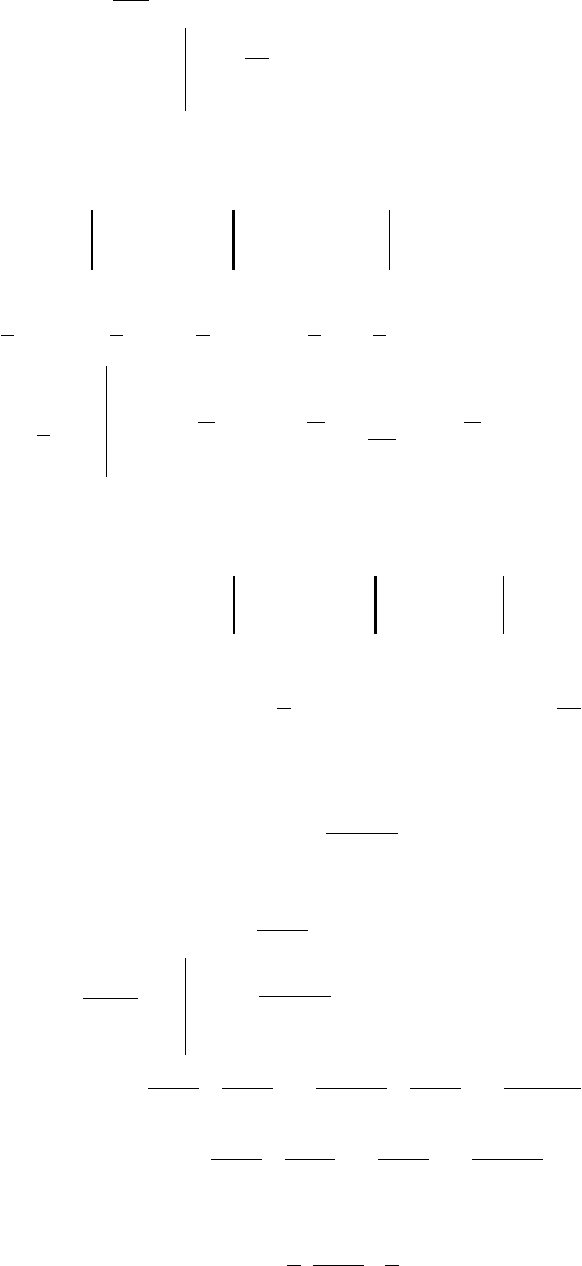
2.
∫∫∫
+−=−=−= Cxxxdxxx
x
xdx
xxxdx lnlnlnln .
u = lnx
x
dx
du =
dv = dx v = x.
Иногда этот метод приходится применять несколько раз.
3
.
∫∫
=+−= xdxxxxxdxx cos2cossin
22
u = x
2
du = 2xdx u
1
= x du
1
= dx
dv = sinxdx
v = −cosx
dv = cosxdx
1
u
1
= sinx
(
∫
−+−= xdxxxxx sinsin2cos
2
)
= −x
2
cosx + 2xsinx + 2cosx + C.
4. Ceexdxxeexdxex
xxxxx
+−−=+−=
−−−−−
∫∫
22
2
22
2
2
3
22222
22.
u = x
2
du = 2xdx
dxxedv
x
2
2
−
=
2
2
22
222
2
xxx
e
x
dedxxev
−−−
−=
−−==
∫∫
.
В некоторых случаях применение этого метода хотя и не избавляет от наличия знака интеграла в
преобразованном выражении, но позволяет получить уравнение относительно исходного интеграла.
5.
(
)
∫∫ ∫
+−=−= xdxexexexdxexexdxe
xxxxxx
sincossincossinsin .
u = sinx du = cosxdx u
1
= cosx
du
1
= −sinxdx
dv = e
x
dx v = e
x
dv
1
= e
x
dx v
1
= e
x
.
Поэтому 2 , откуда
∫
+−=
1
cossinsin Cxexexdxe
xxx
()
∫
+−= Cxxexdxe
xx
cossin
2
1
sin , где
2
1
C
C = .
6. В некоторых случаях интегрирование по частям следует применить к "простому" интегралу,
чтобы получить более сложный. Найдем, например, интеграл
()
∫
+
2
2
1 x
dx
= I.
Для этого проинтегрируем по частям известный интеграл
∫
+=
+
Cx
x
dx
arctg
1
2
, полагая
2
1
1
x
u
+
=
()
2
2
1
2
x
xdx
du
+
−=
dv = dx v = x.
() ()
∫∫∫
+
−+
+
+
=
+
+
+
=
+
dx
x
x
x
x
x
dxx
x
x
x
dx
2
2
2
2
2
2
2
22
1
11
2
1
1
2
11
;
()
∫∫∫
+
−
+
+
+
=
+
2
2
222
1
2
1
2
11
x
dx
x
dx
x
x
x
dx
.
После простых преобразований окончательно получаем
Cx
x
x
I ++
+
⋅= arctg
2
1
12
1
2
.
