Бабайцев В.А.,Браилов А.В.,Винюков И.А.,Рябов П.Е. Учебник по Высшей математике
Подождите немного. Документ загружается.


Признак сравнения. Пусть функции
(
)
xf и
(
)
xg определены на промежутке bxa
<
≤
и
интегрируемы на каждом отрезке
[]
ε
−
ba, , ab
−
<
<
ε
0 . Если
(
)(
xgxf
)
≤
≤
0
∫
b
a
()
∫
b
a
dxxg.
, то из сходимости
интеграла
вытекает сходимость интеграла , причем ≤ из
расходимости интеграла
вытекает расходимость интеграла
()
∫
b
a
dxxg
()
dxxf
∫
b
a
()
dxxf
()
dxxg;
∫
b
a
()
∫
b
a
dxxf
Признак абсолютной сходимости. Пусть функция
(
)
xf определена на промежутке bxa
<
≤
и
интегрируема на каждом отрезке
[]
ε
−
ba, ; тогда из сходимости интеграла следует
сходимость интеграла
()
∫
b
a
xf || dx
()
∫
b
a
dxxf.
В этом случае интеграл называется абсолютно сходящимся. Если же интеграл
сходится, а интеграл
расходится, то интеграл называется условно сходящимся.
()
∫
b
a
dxxf
dx
()
∫
b
a
dxxf
()
∫
b
a
xf ||
()
∫
b
a
dxxf
Аналогичные признаки справедливы и для несобственных интегралов , где f(х) не ограничена
справа от точки
a.
()
∫
b
a
dxxf
Примеры
Исходя из определения, вычислить следующие несобственные интегралы (или доказать их
расходимость):
1.
==
+
+→
+
+→
∫∫
e
ee
x
xx
dx
xx
dx
ε
ε
ε
ε
1
3
2
00
1
3
00
1
3
ln
2
3
lim
ln
lim
ln
=
.
2
3
)1(ln
2
3
2
3
lim
3
2
00
=
+−=
+→
ε
ε
2. =+==
−
+→
−
+→
∫∫
ε
π
ε
ε
π
ε
π
π
2
0
00
2
0
00
2
0
)
42
lntg(lim
cos
lim
cos
x
x
dx
x
dx
.)
22
lntg(lim
00
∞=−=
+→
επ
ε
Следовательно, данный интеграл расходится.
Упражнения
Найти несобственные интегралы или установить их расходимость.
2.4.2.1. .
∫
1
0
ln xdx
2.4.2.2.
∫
−
2
1
x
dx
.
2.4.2.3.
∫
−
1
0
2
1 x
dx
.
2.4.2.4.
∫
−
3
2
2x
xdx
.
2.4.2.5.
()
∫
−
2
0
3
2
1x
dx
.
2.4.2.6.
∫
1
0
2
ln xx
dx
.
2.4.2.7.
∫
4
0
ln
e
xx
dx
.
2.4.2.8.
∫
+
1
0
42
xx
dx
.
2.4.2.9.
()
∫
−
1
0
1 xx
dx
.
2.4.2.10.
∫
−
−
1
0
4
1
4
3
1
dx
x
x
.
2.4.2.11. .
∫
1
0
2
ln xdxx

2.4.2.12. Доказать, что определяющий гамма функцию интеграл сходится при s > 0 и
проверить следующие свойства: а) Г(
s + 1) =sГ(s); б) Г(n + 1) = n!
()
∫
∞
−−
=Γ
0
1
dxexs
xs
2.4.2.13. Дайте определение несобственного интеграла от неограниченной функции. Сходится ли интеграл
∫
1
0
x
dx
? Ответ обоснуйте.
2.4.2.14. Дайте определение несобственного интеграла от неограниченной функции. Сходится ли интеграл
∫
−
1
0
2
1 x
dx
? Ответ обоснуйте.
§ 2.5. Приближенное вычисление интегралов
Приближенное вычисление интегралов применяют обычно в тех случаях, когда точное вычисление
искомого интеграла сопряжено с трудностями, а для практических целей достаточно знать его
приближенное значение, или когда первообразная не является элементарной функцией. Укажем несколько
примеров неопределенных интегралов такого вида:
∫∫ ∫∫∫∫∫∫
−
dxxxdxxdx
x
e
dxxdxe
x
dx
dx
x
x
dx
x
x
x
x
sin;tg;;sin;;
ln
;
cos
;
sin
2
2
и т.д.
Наиболее распространенными являются следующие формулы численного интегрирования. В
приведенных ниже формулах приняты следующие обозначения:
n − число равных отрезков, на которые разбивают отрезок интегрирования [a, b], в формулах
прямоугольников и Симпсона
n − четное число;
y
0
, y
1
, …, y
n
− значения функции f(x) соответственно в точках деления x
0
= a, x
1
, …, x
n
= b.
1.
Формула прямоугольников:
()
(
)
()
131
2
−
+++
−
≈
∫
n
b
a
yyy
n
ab
dxxf K .
2.
Формула трапеций:
()
+++
+−
≈
−
∫
11
0
2
n
n
b
a
yy
yy
n
ab
dxxf K
.
3.
Формула Симпсона (парабол):
() ()(
[]
2421310
24
6
−−
+++++++++
−
≈
∫
nnn
b
a
yyyyyyyy
n
ab
dxxf KK
)
.
Из приведенных формул наиболее точной является формула Симпсона.
Примеры
1.
Найти приближенно интеграл , применяя формулы прямоугольников и трапеций при n = 10.
∫
4
0
2
dxx
Решение. Точное значение данного интеграла находим по формуле Ньютона–Лейбница:
33,21
3
64
3
4
0
3
4
0
2
≈==
∫
x
dxx
. Для приближенного вычисления интеграла по первым двум формулам находим
абсциссы точек деления и соответствующие значения функции:
10,,1,0,;4,0;4,0
2
K===∆⋅==
−
=∆ ixyixix
n
ab
x
iii
.
i 0 1 2 3 4 5 6 7 8 9 10
x
i
0 0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0
y
i
0 0,16 0,64 1,44 2,56 4,0 5,76 7,84 10,24 12,96 16
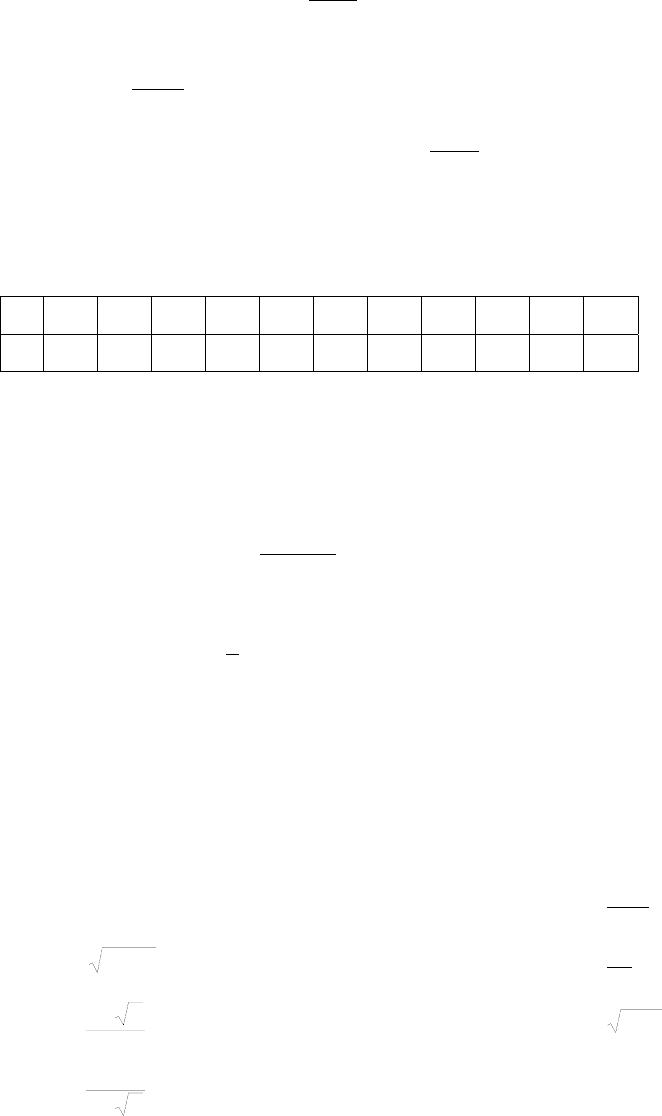
(
12,2196,1284,7444,116,08,0
4
0
2
=++++≈
∫
dxx
)
– по формуле прямоугольников.
Первая формула дает результат с недостатком, абсолютная погрешность ∆ = |21,33−21,12| = 0,21, а
относительная погрешность %98,0%100
33,21
21,0
=⋅=
δ
.
По формуле трапеций имеем:
≈
∫
4
0
2
dxx =
+++++++++
+
≈ 96,1224,1084,776,5456,244,164,016,0
2
160
4,0
44,21
=
.
В этом случае ∆=|21,33−21,44|=0,11, а
%51,0%100
33,21
11,0
=⋅=
δ
. Точность достаточна для большинства
расчетов.
2. Для нахождения затрат на строительство плотины требуется найти площадь поперечного сечения
реки в выбранном для работы месте. Ширина реки равна 20 м, промеры глубины в поперечном сечении через
каждые 2 м приведены в следующей таблице:
x
i
0 2 4 6 8 10 12 14 16 18 20
y
i
0,2 0,5 0,9 1,1 1,3 1,7 2,1 1,5 1,1 0,6 0,2
x − расстояние в метрах от одного из берегов,
y − соответствующая глубина реки в метрах.
Решение. Точное значение площади поперечного сечения реки является интегралом от функции
профиля дна реки, про которую нам известны только вышеуказанные значения. Найдем его приближенное
значение по формуле трапеций:
()
2
м226,01,15,11,27,13,11,19,05,0
2
2,02,0
2 =
+++++++++
+
=
S
.
По формуле Симпсона:
()()
[]
()
2
м93,221,11,23,19,026,05,17,11,15,042,02,0
3
2
=++++++++++=S
Результаты очень близкие, но о точности их говорить не приходится, т.к. мы не знаем точный профиль
реки.
Упражнения
Найти интегралы с точностью до 0,001, применяя формулы: а) прямоугольников, б) трапеций, в)
Симпсона. Сравнить полученный результат с точным значением интеграла, найти абсолютную и
относительную погрешность:
2.5.1. (n = 6).
∫
π
0
sin xdx
2.5.2.
∫
+
1
0
1 x
dx
(n = 10).
2.5.3.
∫
−
+
6
4
2
9dxx (n = 10).
2.5.4.
∫
2
1
x
dx
(n = 10).
2.5.5.
∫
+
2
1
2
1
dx
x
x
(n = 6).
2.5.6.
∫
+
3
1
1dxx (n = 6).
2.5.7.
∫
+
4
0
1 x
dx
(n = 6).

Глава 3
Двойной интеграл
§ 3.1. Определение двойного интеграла и его свойства
Подобно тому, как задача вычисления площади криволинейной трапеции приводит к определенному
интегралу от функции одной переменной, аналогичная задача вычисления объема тела приводит к понятию
двойного интеграла. Определение последнего мало отличается от определения определенного интеграла
для функции одной переменной.
1°. Определение двойного интеграла
Пусть ) – ограниченная функция двух переменных, заданная на ограниченном множестве .
Разобьем
с помощью некоторого набора кривых линий на части , называемые ячейками. В
каждой ячейке
G выберем точку ) и составим сумму
,( yxf
i
G
G
n
GGG ,,,
21
K
,(
ii
yx
(3.1)
∑
=
n
i
iii
yxf
1
,),(
σ
где
– площадь ячейки ). Эта сумма зависит как от выбора разбиения множества , так и от
выбора точек )(
в ячейках. Она называется интегральной суммой.
HG ∪ ( ba < G
,
ii
yx
Обозначим само разбиение через
. Пусть – максимум расстояния между точками ячейки ;
число
называется диаметром ячейки. Наибольшее из чисел назовем диаметром разбиения
G
i
d
i
G
G
n
ddd ,,,
21
K
T
и обозначим ). На рис. 3.1 показано разбиение прямоугольной области на 4 ячейки; диаметр ячейки
– это расстояние между точками
(Td
1
G
P
и Q .
P
Q
G
1
G
2
G
3
G
4
Рис. 3.1
Число ) характеризует "степень мелкости" разбиения (Td
T
; чем меньше это число, тем мельче
разбиение
T
. Если разбиения выбираются так, что при , то будем говорить о
неограниченном измельчении разбиения множества G .
K,,
21
TT 0
}
)
i
T( →d ∞→i
Определение. Если при , т.е. при любом неограниченном измельчении разбиения множества
, интегральная сумма (3.1) стремится к определенному пределу, то этот предел называется
двойным
интегралом от функции
по и обозначается . В этом случае функция
называется интегрируемой в G.
0)( →Td
),( yxf
G
(f
G
∫∫
G
dxdyyxf ),(
), yx
2°. Геометрический смысл двойного интеграла
Пусть 0 в области ),( ≥yxf
{
dycbxaP
≤
≤
≤≤= , . Для любой области определим тело PG ⊆
)}.,(0,),(:),,{(),(
yxfzGyxzyxGfC ≤≤∈∈=
3
R

С геометрической точки зрения )
– “столбик” с основанием , ограниченный сверху
поверхностью ) (рис. 3.2). Объем тела ) обозначим Vf .
,(
GfC
C
G
,( yxfz = ,( Gf (, )G
G
x
y
z
C(f, G )
P
Рис. 3.2
Для неотрицательной функции интеграл от по области , равен объему тела
, ограниченного снизу областью , а сверху – поверхностью )
f
∫∫
G
dxdyyxf ),( f
z
G
),(
GfV G ,( yxf
=
(графиком функции).
3°. Для каких функций существует двойной интеграл?
Теорема. Пусть функция определена и непрерывна на ограниченном множестве , причем
площадь границы этого множества равна нулю. Тогда существует двойной интеграл
),( yxf G
∫∫
G
fdxdy.
Теорема. Пусть – ограниченное множество, – ограниченная функция на , Γ – объединение
границы и множества точек разрыва на . Предположим, что площадь Γ равна нулю. Тогда
существует интеграл
G
∫∫
G
f G
G f G
fdxdy.
4°. Свойства двойного интеграла
1) Если существует интеграл от функции 1
f
≡
по G, то его значение совпадает с площадью области
интегрирования:
∫∫
=
G
Gdxdy ),(1
σ
(3.2)
где )(
G
σ
– площадь . G
2) Справедливо равенство
(3.3)
где
C const.
,
∫∫ ∫∫
=
GG
fdxdyCCfdxdy
3) Если функции
1
f
и
2
f
интегрируемы по области G , то справедливо равенство
(3.4)
∫∫ ∫∫ ∫∫
+=+
GGG
dxdyfdxdyfdxdyff .)(
2121
4) Если
и – две функции, интегрируемые в G , и
1
f
2
f
21
ff
≤
, то
∫∫ ∫∫
≤
GG
dxdyfdxdyf .
21
5) Если )
во всей области G , то
(
constCf ≤
∫∫
≤
G
GCfdxdy ).(
σ
6) Если функция
интегрируема в областях G и f H, HG
∩
, то интегрируема в и f HG ∪
∫∫ ∫∫ ∫∫ ∫∫
∪∩
−
+
=
HGGHHG
fdxdyfdxdyfdxdyfdxdy .
7) Если функция
ограничена на множестве нулевой площади, то f G
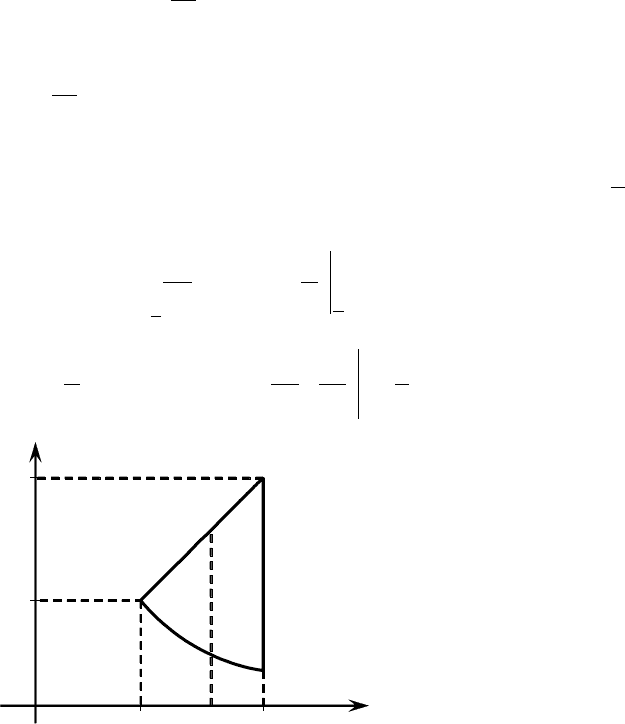
∫∫
=
G
fdxdy .0
8) Свойство аддитивности интеграла. Если область интегрирования
функции разбита на две
части
G таким образом, что площадь
G f
BA ∪=
B
A
∩
равна нулю, а интегрируема по и по f A
B
, то
∫∫ ∫∫ ∫∫
+
=
GAB
fdxdyfdxdyfdxdy .
5°. Сведение двойного интеграла к повторному
Пусть область – криволинейная трапеция, ограниченная слева и справа прямыми G a
x
=
и bx
=
, снизу – графиком функции , )( ba < ) ],[ bax(
1
xgy =
∈
, сверху – графиком , . Тогда
справедлива следующая теорема, сводящая нахождение двойного интеграла к последовательному
вычислению двух интегралов от функций одной переменной.
),[ ba∈(
2
xgy = ]x
Теорема. Если функция интегрируема в области G и при любом фиксированном ),( yxf
x
из
существует интеграл
, то справедлива формула
],[ ba
∫
)(
)(
2
1
,(
xg
xg
x )dyyf
(3.5)
∫∫ ∫ ∫
=
G
b
a
xg
xg
dxdyyxfdxdyyxf .),(),(
)(
)(
2
1
Замечание. Выражение называется повторным интегралом и часто записывается в
виде
∫∫
b
a
xg
xg
dxdyyxf
)(
)(
2
1
),(
.),(
)(
)(
2
1
∫∫
b
a
xg
xg
dyyxfdx
Примеры
1. Вычислить интеграл от функции
2
2
),(
y
x
yxf
=
по области G , ограниченной прямыми xyx
=
=
,2 и
гиперболой 1 (рис. 3.3). =xy
Решение. Функция
2
2
),(
y
x
yxf
=
G Ox
непрерывная в области , следовательно, интегрируема в этой
области. Проекция области на ось есть отрезок При фиксированном значении
G
].2,1[
x
из этого
отрезка соответствующая прямая, параллельная оси
, пересекает область по отрезку Oy G .xy ≤≤
1
x
Поэтому, согласно формуле (3.5),
∫∫
∫∫ ∫ ∫ ∫
=
−=−=
−=
=
−==
2
1
2
1
2
1
24
32
1
2
1
1
2
1
2
2
2
.
4
9
24
)(
1
1
),(
xx
dxxxdx
x
xx
dx
y
xdy
y
x
dxdxdyyxf
x
x
G
x
x
1
2
2
1
x
y
x
xy = 1
G
Рис. 3.3

2. Вычислить интеграл от функции xyxf
=
),( по области G, где G треугольная область с вершинами
)C (рис. 3.4).
),1,1(
=A ),5,4(=B 2,6(=
Решение. Представим треугольную область
G в виде объединения двух множеств G
1
и G
2
.
Уравнения прямых имеют вид:
.
3
4
:,
2
322
:,
3
14
:
+
=
−
=
−
=
x
yAC
x
yBC
x
yAB
Тогда
∫∫ ∫∫ ∫∫ ∫∫
∪
=+==
GGGGG
xdxdyxdxdyxdxdyxdxdy
2112
=
() ()
∫∫ ∫∫∫∫
=+=
+
−
=
+
=
−
=
+
=
−
+
−
+
6
4
4
1
6
4
2
322
5
4
3
14
5
4
2
322
5
4
3
14
5
4
4
1
dxxydxxydyxdyxdx
xx
y
x
y
x
y
x
y
x
x
x
x
=
∫∫
=
−+
−
4
1
6
4
22
10
17
5
51
15
17
15
17
dxxxdxxx
=
.
6
187
15
238
10
153
30
17
10
51
30
17
45
17
6
4
32
4
1
23
=+=
−+
−
xxxx
5
2
x
y
1
41 6
A
C
B
2
G
0
1
G
Рис. 3.4
Непосредственно из определения двойного интеграла следует, что если функция ) интегрируема
в и множество симметрично относительно оси , то из равенства
(четности
функции ) относительно переменной ) следует, что
,( yxf
,() xf
−=
G G Ox ),( yyxf
,( yxf y
∫∫ ∫∫
=
GG
dxdyyxfdxdyyxf
1
,),(2),(
где
G , а из равенства
{
0:),(
1
≥∩= yyxG
}
),(),( yxfyxf
−
−
=
(нечетности ) относительно переменной
) следует, что Так, например, сразу можно утверждать, что интеграл
где
,( yxf
y
∫∫
G
∫∫
G
f
++ dxdyyx ,)1(
242217
=dxdyyx .0),(
y
{
}
2244
: yxyx +≤+)
Oy
,( yxG = равен нулю. Аналогичные равенства
справедливы, если симметрично относительно оси , а функция ) четна или нечетна
относительно переменной
G , yx(f
x
.
3. Найти площадь фигуры, ограниченной параболами
95
2
+= xy и .13
2
+−= xy
Решение. Вершины параболы находятся на оси Ox в точках
−
0,
4
9
и
0,
3
1
(рис. 3.5). Заданные
параболы образуют область G , площадь которой требуется найти:
∫∫
=
G
dxdyG .1)(
σ
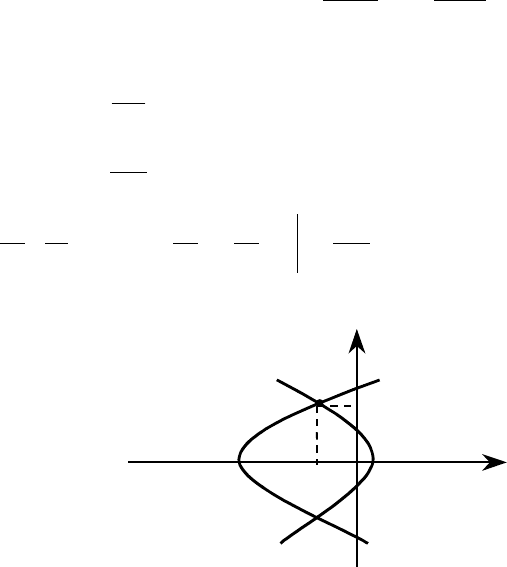
Заметим, что область симметрична относительно оси , а функция 1
четна, в частности по
переменной . Следовательно, имеем:
G Ox ),(
=yxf
y
∫∫ ∫∫
=
=
GG
dxdydxdyG
1
,2)(
σ
где Найдем точки пересечения парабол в области :
{}
.0:),(
1
≥∩= yyxGG
1
G ,1395
+
−=+ xx отсюда
Таким образом, область G определяется системой неравенств .2,1 =− y=x
1
.
3
1
5
9
,20:),(
22
1
−
≤≤
−
≤≤=
y
x
y
yyxG
Тогда
∫∫ ∫ ∫
=
==σ
−
−
1
2
2
2
0
3
1
5
9
22)(
G
y
y
dxdydxdyG
=
∫
=
−=
−
2
0
2
0
32
.
45
256
45
8
15
32
2
15
8
15
32
2 yydyy
-1
2
x
y
2
31yx
=
−+
2
59yx=+
1
G
Рис. 3.5
Иногда при вычислении двойных интегралов приходится сталкиваться с задачей изменения порядка
расстановки пределов интегрирования в повторном интеграле .
Для решения такой задачи
сначала делаем переход от заданного повторного интеграла к двойному:
),(
)(
)(
2
1
∫∫
b
a
xg
xg
dyyxfdx
∫∫∫∫
=
b
aG
xg
xg
dxdyyxfdyyxfdx .),(),(
)(
)(
2
1
Условия на координаты точек )( множества G получаем исходя из заданного повторного интеграла: , yx
)}.()(,:),{(
)}()(,:),{(
11
21
yhxyhdycyx
xgyxgbxayxG
≤≤≤≤
=
≤
≤
≤
≤
=
Таким образом, получаем цепочку равенств:
∫∫∫∫∫∫
==
d
c
yh
yh
b
aG
xg
xg
dxyxfdydxdyyxfdyyxfdx
)(
)(
)(
)(
2
1
2
1
.),(),(),(
Обычно средний член этой цепочки (двойной интеграл) только подразумевается (как общее значение
равных повторных интегралов), но не записывается.
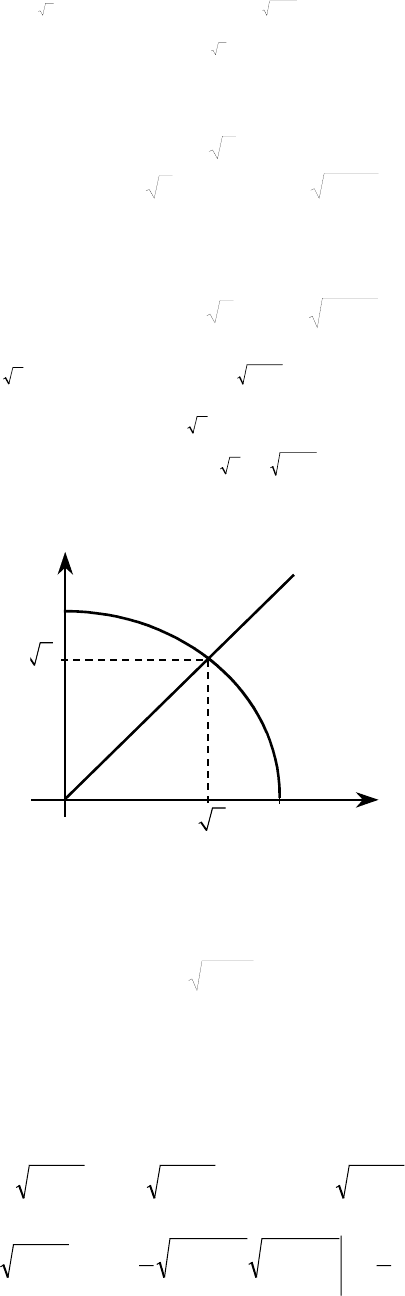
4. Изменить порядок интегрирования и свести к одному повторному интегралу
∫∫∫∫
+
−2
2
4
00
2
0
.),(),(
2
xx
dyyxfdxdyyxfdx
Решение. Начнем с того, что запишем условия на координаты точек ) из множеств
и ,
по которым берутся повторные интегралы:
,( yx
1
G
2
G
{
}
{}
.40,22:),(
,0,20:),(
2
2
1
xyxyxG
xyxyxG
−≤≤≤≤=
≤≤≤≤=
Тогда (рис. 3.6.)
,
21
GGG
=
∪
где
{
}
.4,20:),(
2
yxyyyxG −≤≤≤≤=
Таким образом,
∫∫ ∫∫
∫∫∫∫
∪=
−
−
==
=
+
21
2
2
.),(),(
),(),(
4
2
0
2
0
4
0
2
2
0
GGG
y
y
xx
dxdyyxfdydxdyyxf
dyyxfdxdyyxfdx
2
2
x
y
2
yx
=
1
G
2
G
2
0
22
4xy
+
=
Рис. 3.6
Перемена порядка интегрирования в повторном интеграле иногда существенно упрощает его
вычисление.
5. Изменив порядок интегрирования, вычислить повторный интеграл
∫∫
−
1
6
2
1
0
.1
x
dyydx
Решение. Внутренний интеграл не является элементарной функцией. Множество
представляет
собой треугольную область и определяется системой неравенств (рис. 3.7):
G
{}
{
}
.0,10:),(1,10:),( yxyyxyxxyxG
≤
≤
≤
≤
=
≤
≤
≤≤
=
Следовательно,
()()
∫
∫∫∫ ∫∫∫
=−−−=−=
=
−=−=−
1
0
1
0
6
7
2
6
7
2
6
2
11
00
6
2
6
2
6
2
1
0
.
7
3
11
7
3
1
111
yyydyy
dxydydxdyydyydx
xG
y
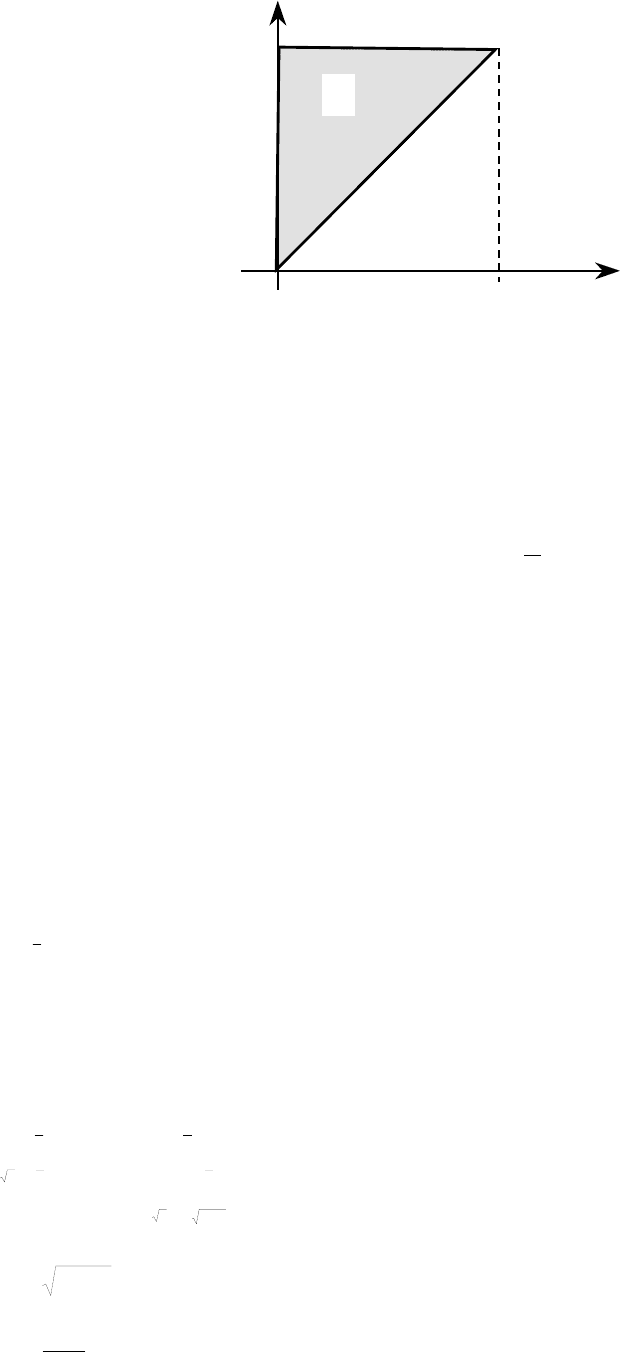
1
x
y
yx
=
G
0
1
Рис. 3.7
Упражнения
Вычислить двойные интегралы:
3.1.1. где
∫∫
+
G
dxdyyx ,)34(
{}
.10,10:),(
≤
≤
≤
≤= yxyxG
3.1.2.
где
∫∫
++
G
dxdyyxx ,)sin()25(
.
2
0,0:),(
≤≤≤≤=
π
π
yxyxG
3.1.3. где
∫∫
+
G
dxdyyx ,)615(
2
{}
.20,10:),(
≤
≤
≤
≤= yxyxG
3.1.4. где
∫∫
−+
G
dxdyyx ,)3)(1(
2
{}
.,10:),(
2
xyxxyxG ≤≤≤≤=
3.1.5. где G ограничено линиями
∫∫
G
dxdyy ,
2
.2,
2
−== xyyx
3.1.6.
где G – треугольник, ограниченный прямыми
∫∫
+
G
dxdyyx ,)( .6,2,2 =+
=
=
yxxyyx
3.1.7.
где G ограничено прямыми
∫∫
+
G
dxdyyx ,)2( ,
x
y
=
,2xy
=
,2
=
x .3
=
x
3.1.8. где G ограничено прямыми
∫∫
+
G
dxdyyx ,)(
22
,
x
y
=
,1
+
=
xy ,1
=
y .3
=
y
3.1.9.
∫∫
G
y
x
dxdye , где ограничено параболой и прямыми G xy =
2
.1,0
=
=
yx
3.1.10.
где
{}
∫∫
G
dxdyyx ,,min
{}
.10,10:),(
≤
≤
≤
≤= yxyxG
Изменить порядок интегрирования и свести к одному повторному интегралу:
3.1.11.
∫∫∫∫
+
y
yy
yxfdydxyxfdy
2
2
4
1
2
2
1
0
).,(),(
3.1.12.
∫∫∫∫
−
+
2
0
2
3
2
3
3
0
.),(),(
2
xx
x
dyyxfdxdyyxfdx .
Изменив порядок интегрирования, вычислить повторные интегралы:
3.1.13.
∫∫
−
2
3
2
2
0
.4
x
dyydx
3.1.14.
∫∫
ππ
y
dx
x
x
dy .
sin
0
