Бабайцев В.А.,Браилов А.В.,Винюков И.А.,Рябов П.Е. Учебник по Высшей математике
Подождите немного. Документ загружается.

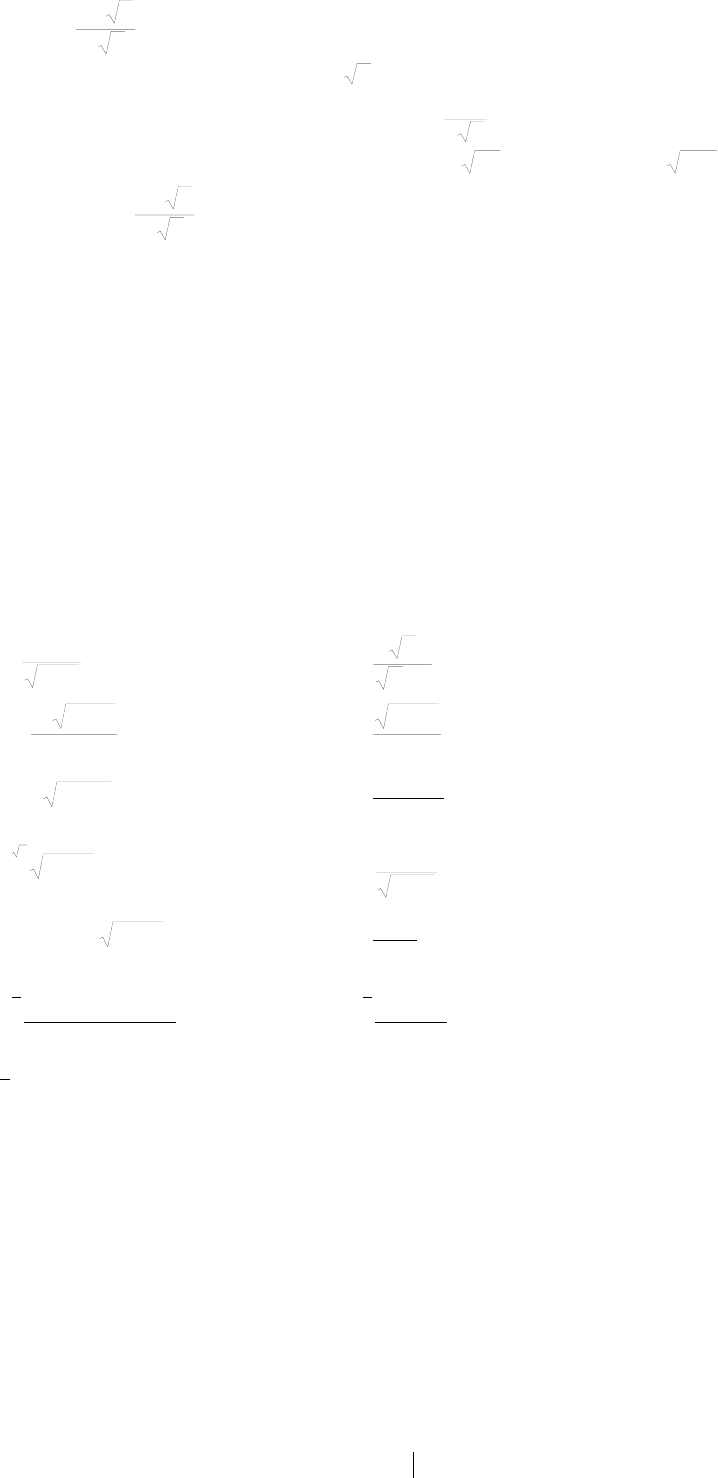
3. Найти dx
x
x
∫
2
2
4
2
sin
π
π
.
Решение. Сделаем замену
xxt == )(
ϕ
и применим вышеприведенную формулу замены справа
налево, поменяв местами
t и x. Тогда
,
2
)(
x
dx
dxxdt =
′
=
ϕ
а новые пределы интегрирования a и b
определятся из условий
ϕ
([
α
,
β
]) = [a, b], откуда a =
ϕ
(
α
)=
π
=
π
2
и
ππβϕ
24)(
2
===b
.
.2)1(1cos2cos|cossin
2
sin
2
24
2
2
−=−+−=+−=−==
∫∫
ππ
π
π
π
π
π
π
tdttdx
x
x
4.
Доказать нечетность функции .
∫∫
−==
−
xx
t
dttdtexg
0
2
0
)exp()(
2
Решение. Для вычисления интеграла
сделаем замену
∫
−
−=−
x
dttxg
0
2
)exp()(
uut
−
== )(
ϕ
. Тогда
,)( duduu −=
′
ϕ
а новые пределы интегрирования
α
и
β
определятся из условий −
α
= 0 и −
β
= −x, откуда
α
=
0 и
β
= x.
∫
−
−=−
x
dttxg
0
2
)exp()(= )()exp())()(exp(
0
2
0
2
xgduuduu
xx
−=−−=−−−
∫∫
,
поскольку переименование переменной интегрирования не изменяет интеграла.
Упражнения
Найти интегралы, применяя метод замены переменной.
2.2.1.1.
∫
+
+
3
0
1
2
dx
x
x
.
2.2.1.2.
∫
−
9
4
1
dx
x
x
.
2.2.1.3.
∫
+
−
5ln
0
3
1
dx
e
ee
x
xx
. 2.2.1.4.
∫
−
2
1
2
1
dx
x
x
.
2.2.1.5.
∫
−
2
0
22
4 dxxx .
2.2.1.6.
()
∫
+
1
0
3
2
1 x
dx
.
2.2.1.7. dxx
∫
+
3
0
2
1.
2.2.1.8. dx
x
x
∫
+
27
0
2
9
.
2.2.1.9. dxxx
∫
−+
1
0
2
1)103(.
2.2.1.10. dx
x
x
∫
+
5
0
3
.
2.2.1.11.
∫
+−
2
0
2
sinsin56
cos
π
dx
xx
x
.
2.2.1.12.
∫
+
−
2
0
cos1
cos1
π
dx
x
x
.
2.2.1.13.
∫
4
0
4
tg
π
xdx .
2.2.1.14. Докажите, что если непрерывная на отрезке ],[ aa
−
функция является четной, то
справедливо равенство
()
xf
dxxfdxxf
aa
a
∫∫
=
− 0
)(2)(.
2.2.1.15. Докажите, что если непрерывная на отрезке ],[ aa
−
функция является нечетной, то
справедливо равенство
.
()
xf
0)( =
∫
−
dxxf
a
a
2°. Интегрирование по частям
Пусть u(x) и v(x) − две непрерывно дифференцируемые функции на отрезке [a, b]. Тогда выполняется
формула интегрирования по частям
∫∫
−=
b
a
b
a
b
a
vduuvudv .

Примеры
1
. Найти .
∫
1
0
arctgxdx
Решение. Применим формулу интегрирования по частям, полагая
u = arctgx
2
1 x
dx
du
+
=
dv = dx v = x.
Тогда имеем
()
=
+−=
+
−=
∫∫
1
0
2
1
0
2
1
0
1
0
1ln
2
1
arctg
1
arctgarctg xxxdx
x
x
xxxdx
4
4ln
2
2ln
4
−
=−=
ππ
.
Упражнения
Найти интегралы, применяя метод интегрирования по частям.
2.2.2.1. .
∫
e
xdx
1
2
ln
2.2.2.2.
∫
2
0
2
sin
π
xdxx .
2.2.2.3.
∫
e
dx
x
x
1
2
ln
.
2.2.2.4.
∫
+
1
0
1
arcsin
dx
x
x
.
2.2.2.5. .
∫
1
0
dxxe
x
2.2.2.6. .
∫
π
0
sin xdxe
x
2.2.2.7.
∫
4
0
2
cos
π
dx
x
x
.
2.2.2.8.
∫
−
1
0
2
1
arcsin
dx
x
xx
.
2.2.2.9. .
∫
1
0
3
arctgxdxx 2.2.2.10. .
∫
π
16
0
8
cos xdx
2.2.2.11.
∫
+
e
xdxx
1
ln)516(.
2.2.2.12.
∫
+
4
0
2
cos
320
π
dx
x
x
.
§ 2.3. Некоторые приложения определенного интеграла
1
°. Нахождение площадей плоских фигур
Криволинейной трапецией называют плоскую фигуру, ограниченную осью Ox, графиком функции y =
f(x) и двумя вертикальными прямыми x = a и x = b. Площадь такой фигуры находят по формуле:
()
∫
=
b
a
dxxfS .
Трапеция может также опираться на ось Oy, располагаться под осью Ox или слева от оси Oy. В этих
случаях площадь находят соответственно по формуле:
∫
=
d
c
xdyS ; ; .
∫
−=
b
a
ydxS
∫
−=
d
c
xdyS
При нахождении площади криволинейной плоской фигуры, ограниченной несколькими кривыми, ее
следует разбить на части, площадь каждой из которых можно найти по одной из приведенных формул.
Примеры
1.
Найти площадь фигуры, ограниченной кривыми
2
1
1
x
y
+
= и
2
2
x
y = .
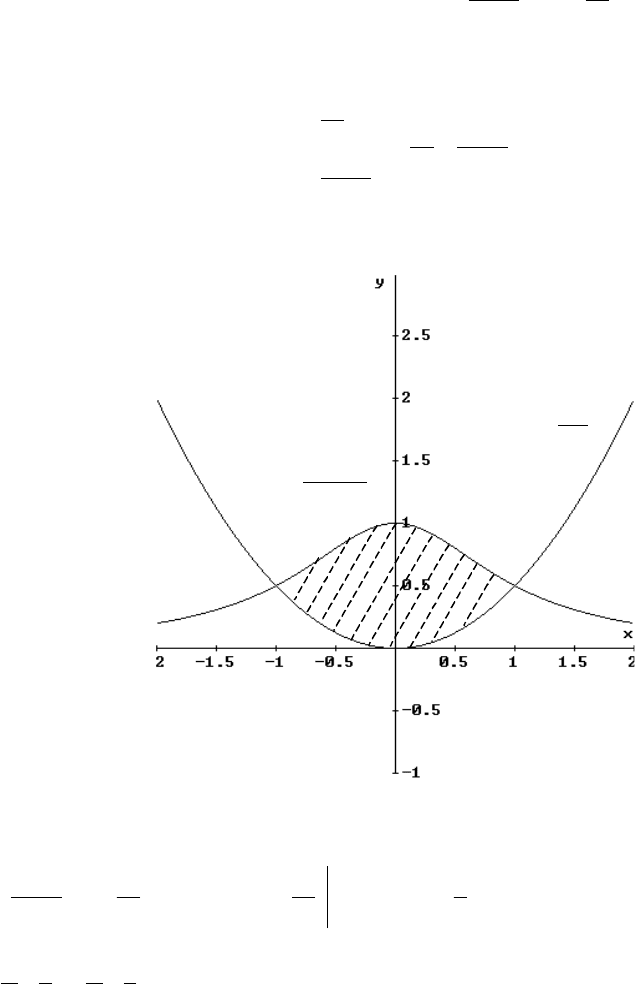
Решение. Построим графики данных кривых (рис. 2.2) и найдем абсциссы точек пересечения
графиков из системы уравнений:
,
1
1
2
,
1
1
,
2
2
2
2
2
x
x
x
y
x
y
+
=⇒
+
=
=
x
4
+ x
2
− 2 = 0, x
2
= 1, x
1,2
= ±1.
2
2
x
y =
2
1
1
x
y
+
=
Рис. 2.2.
Поскольку данная фигура симметрична относительно оси Oy, то имеем:
=
−=
−=
−
+
=
∫∫
6
1
1arctg2
6
arctg2
21
1
2
1
0
3
1
0
2
1
0
2
x
xdx
x
dx
x
S
.
3
1
26
1
4
2 −=
−=
ππ
2.
Найти площадь фигуры, ограниченной линиями y = lnx,
y = 0, y = 1 и x = 0.
Решение. Построим на графике данные линии (рис.2.3). Искомую площадь можно найти двумя
способами: 1) как площадь трапеции, опирающейся на ось ординат (более рационально в данном случае); 2)
как разность площадей двух трапеций, опирающихся на ось Ox.
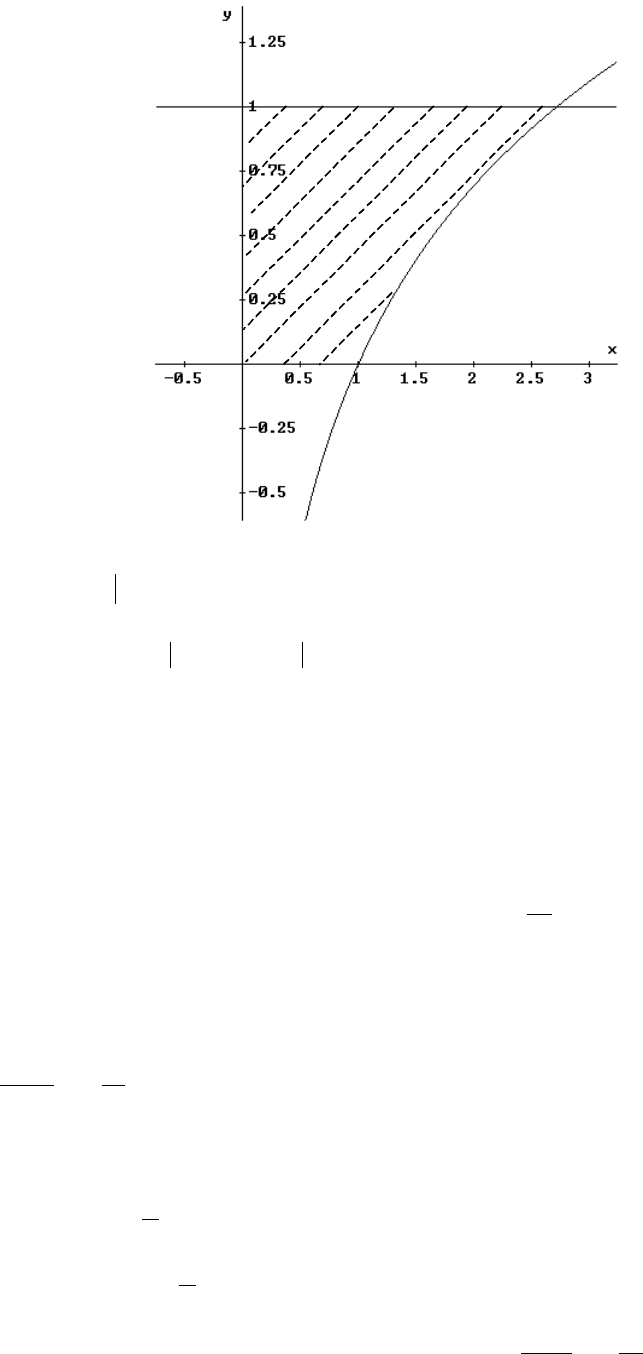
y
= ln
x
y
= 1
Рис. 2.3.
1) .1
1
0
1
0
−===
∫
eedyeS
yy
2)
e
ee
xxdxdxS
1
10
ln =−=
∫∫
()
=−+−=−⋅− 1ln
1
eeexxx
e
e − 1.
Второй интеграл мы нашли интегрированием по частям. Результаты, разумеется, одинаковые.
Упражнения
Найти площадь фигур, ограниченных линиями.
2.3.1.1. y = x
2
, y = 0, x = 3.
2.3.1.2. y = 3x
2
−4x + 8, y = 0, x = −1, x = 2.
2.3.1.3. y = 3x − x
2
, y = 0.
2.3.1.4. 1
4
2
2
=+
y
x .
2.3.1.5. xy = 6, x = 1, x = 6, y = 0.
2.3.1.6. y = lnx, y = 0, x = e.
2.3.1.7. y
2
= (4 − x)
3
, x = 0.
2.3.1.8. y = 4x − x
2
, y = −x − 6. 2.3.1.9. y = x
2
− 3x − 4, y = –x
2
+ 4x.
2.3.1.10.
6
,
9
27
2
2
x
y
x
y =
+
= .
2.3.1.11. x
2
+ y
2
= 4, x
2
+ (y − 2)
2
= 8.
2.3.1.12. y
2
= 9x, x
2
=9y. 2.3.1.13. xy = 6, x + y = 7.
2.3.1.14. y = cos
2
x, x = 0, x = 2
π
, y = 0.
2.3.1.15. y = tgx, y = 0,
4
π
=x .
2.3.1.16. y = arcsinx, x = 0,
2
π
=y .
2.3.1.17. y = x
2
−3x, y = 12 − 4x.
2.3.1.18.
2
,
1
1
2
2
x
y
x
y =
+
= .
2.3.1.19. xy = 16, x + y = 10.
2.3.1.20. y = x
2
+ 2x − 3, y = 0.
2°. Нахождение объемов тел вращения
Объем тела вращения, полученного вращением криволинейной трапеции, равен:
а) вокруг оси Ox:
V ;
∫
=
b
a
dxy
2
π
б) вокруг оси Oy:
V .
∫
=
d
c
dyx
2
π
Примеры
1.
Найти объем тела, полученного от вращения фигуры, ограниченной линиями y
2
= 9x + 27 и y = x +
3, вокруг оси Ox.
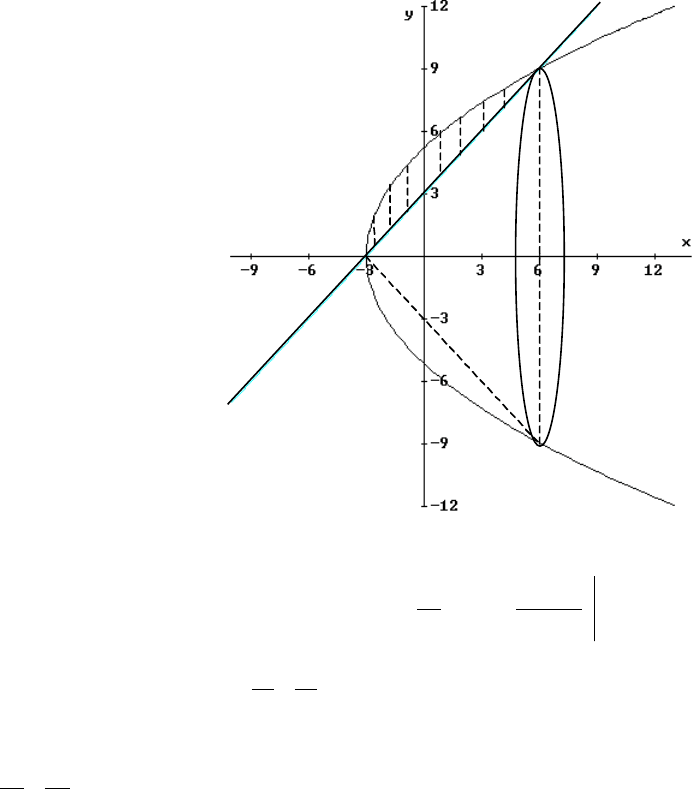
Решение. Построим линии, заданные уравнениями.
y
2
= 9
x
+ 27
Рис. 2.4
()()
()
=
+
−+=+−+=
−
−−
∫∫
6
3
3
2
6
3
2
6
3
3
3
27
2
93279
x
x
x
dxxdxxV
x
πππ
ππ
5,1110327
2
81
3
9
627189
3
=
+⋅+−−⋅+⋅= .
2. Найти объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной линиями:
1
2
2
2
2
=−
b
y
a
x
, y = b, y = −b (рис. 2.5).
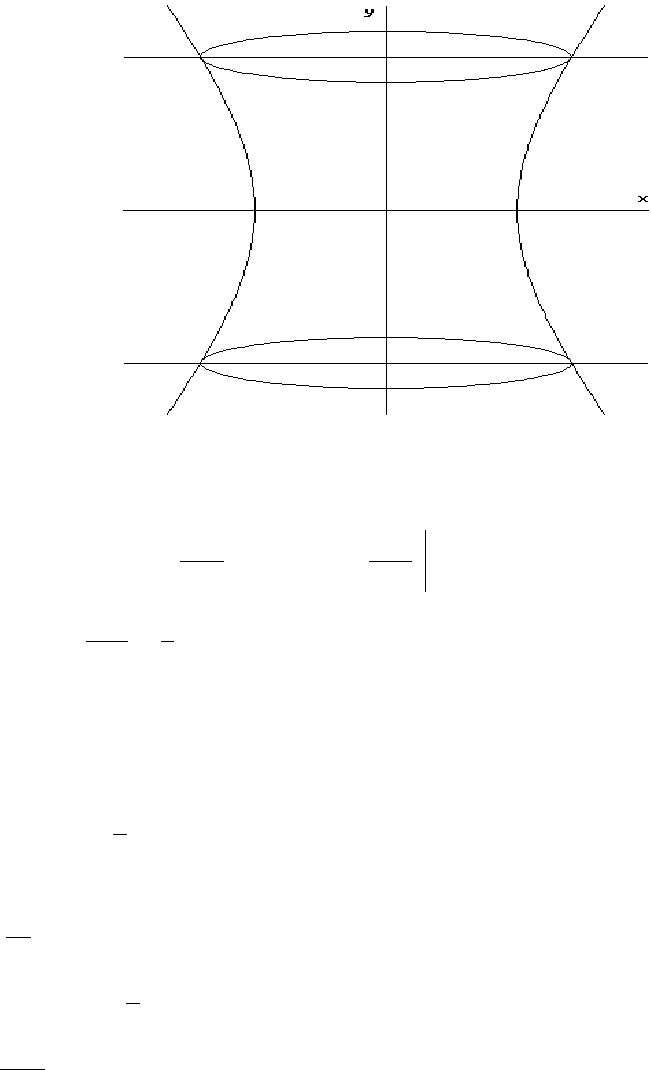
b
−
b
−
aa
Рис. 2.5.
Решение.
=
+=
+==
∫∫
−
b
bb
b
b
ya
yady
b
ya
adyxV
0
2
32
2
0
2
22
22
3
22
πππ
.
3
8
3
2
2
2
32
2
ba
b
ba
ba
ππ
=
+=
Упражнения
Найти объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями.
2.3.2.1. y
2
= 2x, x = 4. 2.3.2.2. xy = 5, x = 1, x = 5, y = 0.
2.3.2.3. y
2
= 4 − x, 2
2
1
+−= xy .
2.3.2.4. y = 4x − x
2
, y = x.
2.3.2.5. y = x
2
, x + y − 6 = 0.
2.3.2.6. y
2
= x, x
2
= y.
2.3.2.7. 1
9
2
2
=+
y
x .
2.3.2.8. 0,2,0,5sin ==
=
+
=
yxxxy
π
.
2.3.2.9.
π
2,0,
2
sin === xx
x
y .
2.3.2.10. x
2
+ y
2
= r
2
.
2.3.2.11. 4,5,
6
2
−=−=
+
= xx
x
y .
Найти объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной линиями:
2.3.2.12. y = x
2
, y
2
= 8x.
2.3.2.13. , y = 2, y = −2. 4
22
=− yx
2.3.2.14. y = arctgx, x = 0, y = 1. 2.3.2.15. y = lnx, x = 0, y = 0, x = e.
2.3.2.16. Найти объем тела, образованного вращением вокруг прямой x = 3 фигуры, ограниченной линиями:
y = 4 − x
2
и y = 0.
3°. Экономические приложения определенного интеграла
Приведем общую схему рассуждений, с помощью которых можно получить решение задачи в виде
определенного интеграла.
Пусть рассматривают некоторый процесс, описываемый переменной x, меняющейся в интервале [x
1
,
x
2
], и некоторой функцией

y = f(x). Допустим, что некоторый показатель процесса A есть произведение величины y на величину
изменения x.
Если f(x) = const, то величина A находится без труда:
A = y(x
2
− x
1
). Если же функция не является константой, то нахождение A требует выполнения ряда
действий:
I. Рассмотрение "бесконечно малого" отрезка dx.
II. Образование "элемента" величины A в виде dA = ydx.
III. Определение A с помощью определенного интеграла.
Часто в качестве независимой переменной фигурирует время t.
Примеры
1.
Определить дневную выработку A рабочего за восьмичасовой рабочий день, если
производительность труда y в течение дня меняется по закону y = y
0
(−0,025t
2
+ 0,2t + 0,6).
Решение. Рассмотрим отрезок времени dt, в течение которого производительность можно считать
приближенно постоянной и равной y. Тогда выработка за этот отрезок времени составит dA = ydt. Всю
дневную выработку найдем с помощью определенного интеграла:
. Подставляя выражение для y и
интегрируя, получим
∫
=
8
0
ydtA
0
8
0
2
3
0
93,66,0
2
2,0
3
025,0
yt
t
tyA =
++
−
= .
Заметим, что если бы работа велась ритмично с максимальной производительностью, равной y(4) = y
0
,
то дневная выработка составила бы
A = y
0
(8 − 0) = 8y
0
,
т.е. на 15% больше.
2. Стоимость перевозки 1 тонны на 1 км − y руб./км (тариф на перевозки) убывает в зависимости от
расстояния и определяется по следующей формуле:
bx
a
y
+
= . Найти зависимость суммарной стоимости
перевозки 1 тонны груза от пройденного пути.
Решение. Обозначим искомую стоимость через A. Согласно условию задачи стоимость перевозки
на расстояние dx составляет dA = ydx рублей. Следовательно, стоимость перевозки 1 тонны груза на
расстоянии x км составит
()
b
bx
abxa
bx
adx
A
x
x
+
=+=
+
=
∫
lnln
0
0
.
3. Объем y ежегодного производства некоторого вида оборудования растет с темпом роста
y
y
k
′
= и
составляет в начальный момент (t = 0) величину y
0
. Определить суммарный объем оборудования,
произведенного к моменту времени t.
Решение. Объем выпущенного оборудования за отрезок времени [t, t + ∆t] составит A = ydt. Из
соотношения для темпа роста найдем:
(
′
=
)
′
= y
y
y
k ln , откуда после интегрирования получим
ty
y
kty
0
0
ln =
или
kt
y
y
=
0
ln . Поэтому y = y
0
e
kt
. Искомую величину определим с помощью интегрирования:
()
1
0
0
0
0
0
0
−====
∫∫
kt
t
kt
t
kt
t
e
k
y
e
k
y
dteyydtA .
Пусть 1
(темп роста 10%), тогда
,0=
k
()(
1101
1,0
1,0
0
1,0
0
−=−=
tt
eye
y
A
)
. Например, через 20 лет получим
A = 10y
0
(e
2
− 1) ≈ 64y
0
.

Упражнения
Задачи с экономическим содержанием.
2.3.3.1. Зависимость потребляемой на бытовые нужды города электроэнергии y (кВт⋅ч) от времени
суток
x (час) выражается следующей формулой:
(
3
12
cos ++= xbay
π
)
. Найти суммарный расход
электроэнергии за сутки. Произвести расчет при следующих числовых данных:
a = 25000 кВт⋅ч, b =
15000 кВт⋅ч.
2.3.3.2. Найти стоимость перевозки 1000 тонн груза по железной дороге на расстояние 1000 км, если
тариф на перевозку одной тонны убывает с каждым следующим километром на постоянную величину
0,5 руб.
2.3.3.3. Функция предельного дохода равна
()
()
2
1
10
q
qMR
+
= . Найти функцию дохода
R(q) и вычислить
ее значение при
q = 9, если известно, что R(0) = 0.
2.3.3.4. Дана функция предельных издержек
()
qqMC arctg
100
π
= . Найти выражение для функции
издержек
C(q) и ее значение при q = 100, если известно, что C(0) = 1000.
2.3.3.5. Дана функция предельного потребления
()
y
yMC
2,0
8,0 += . Найти выражение для функции
потребления
C(y) и ее значение при y = 400, если известно, что C(100) = 100.
2.3.3.6. Пусть скорость изменения денежного потока задана функцией
(
)
3
20 ttI = . Найти зависимость
величины денежного потока
K(t) от времени t и величину накоплений на интервале [1, 64], если
известно, что
K(0) = 50.
2.3.3.7. Рассматривается непрерывный денежный поток, прибывающий с постоянной скоростью 1 млн
руб./год. Найти его дисконтированное значение в течение двух лет для непрерывных 5%. Аналогичный
вопрос для интервала в три года и 4%.
2.3.3.8. Пусть скорость изменения денежного потока задана функцией I(t) = 40 + 0,05t. Найти
дисконтированное значение денежного потока за 5 лет при непрерывных 5%.
§ 2.4. Несобственные интегралы
1
°. Несобственные интегралы с бесконечными пределами
Пусть функция f(x) определена для всех a
x
≥
dxxf )(
и интегрируема на любом отрезке [а, b]. Тогда
называется несобственным интегралом от f(x) в пределах от а до +∞ и обозначается
. Аналогично определяются интегралы и .
∫
+∞→
b
a
b
dxxf )(
lim
∫
+∞
a
dxxf )(
∫
∞−
b
∫
+∞
∞−
dxxf )(
Таким образом,
∫
+∞
a
dxxf )(= ; ;
∫
+∞→
b
a
b
dxxf )(
lim
∫
∞−
b
dxxf )(=
∫
−∞→
b
a
a
dxxf )(
lim
∫
+∞
∞−
dxxf )(=
∫
−∞→
c
a
a
dxxf )(
lim
+ .
∫
+∞→
b
c
b
dxxf )(
lim
Если приведенные пределы существуют и конечны, то соответствующие интегралы называются
сходящимися. В противном случае интегралы называются расходящимися.
Признак сравнения. Пусть функции и определены для всех a)(xf )(xg
x
≥ и интегрируемы на
каждом отрезке
[а, b], . Если ab ≥ )() xg(0 xf
≤
≤ для всех a
x
≥ , то из сходимости интеграла
∫
+∞
a
dxxg )(

вытекает сходимость интеграла , причем ≤ ; из расходимости интеграла
вытекает расходимость интеграла .
∫
+∞
a
dxxf )(
∫
+∞
a
dxxf )(
∫
+∞
a
dxxg )(
∫
+∞
a
dxxf )(
∫
+∞
a
dxxg )(
)x
∫
+∞
a
xf
dx
∫
+∞
a
xf |)(|
)xf
at
t
=
→
)
α
→
lim
t
α
dt(.
∫
+∞
a
dxx)(=
∫
β
α
′
ϕϕ
tf ())(
=
∫
∞
1
3
ln xx
dx
∫
+∞
b
x
dx
1
3
ln
lim
x 8
11
2
2
=
b
e
x2
lim
=
+∞→b
dx
x
+
∫
b
b
x
x
1
1
sin
2
/|sin xx ≤
∫
∞
1
2
1
dx
x
∫
∞
1
cos
dx
x
x
dx
dx
x
Признак абсолютной сходимости. Пусть функция определена для всех (f a
x
≥ . Если
интеграл сходится, то сходится и интеграл , причем
∫
+∞
a
dxxf |)(| dx)(
∫
+∞
a
dxxf )( ≤
∫
+∞
a
f|.dxx |)(
Если интеграл сходится, а расходится, то интеграл называется
условно сходящимся.
∫
+∞
a
dxxf )(
∫
+∞
a
dxxf )(
Замена переменной в несобственном интеграле основывается на следующей теореме.
Теорема. Пусть функция определена и непрерывна при ( a
x
≥ .
Если функция x= φ(t), определенная на промежутке α
< t < β (α и β могут быть и символами −∞ и +∞
соответственно),
имеет непрерывную производную φ'(t) ≠ 0 и
(
lim
ϕ
, +∞=
′
)(t
ϕ
, то
f t)
Примеры
1
. Вычислить несобственный интеграл с бесконечным пределом
∫
∞
1
3
ln xx
dx
, основываясь на
определении несобственного интеграла.
Решение. По определению,
→
b
ln
−
.
2. Доказать сходимость несобственного интеграла с бесконечным пределом
∫
∞
1
cos
dx
x
x
.
Решение.
∫
∞
1
cos
dx
x
x
=
∫
+∞→
b
b
dx
x
x
1
cos
lim
=
+∞→b
x
2
sin
lim
=
∫
∞
+
1
2
sin
1sin
dx
x
x
−
Интеграл
∫
∞
1
2
sin
dx
x
x
сходится (причем абсолютно), т.к. при , а интеграл
2
/1| x 1≥x
сходится. Таким образом сходится и интеграл .
3
. Доказать расходимость несобственного интеграла
∫
∞
1
|cos|
x
x
.
Решение . Действительно,
x
x
x
x
x
x
2
2cos1cos|cos|
2
+
=≥ .
Интеграл
∫
∞
+
1
2
2cos1
dx
x
x
=
∫
+∞→
b
b
x
dx
1
2
1
lim
∫
∞
−
1
2cos
2
1
dx
x
x
= b
b
ln
2
1
lim
+∞→
∫
∞
−
1
2cos
2
1
x
расходится, т.к. ∞=
+∞→
ln
2
1
lim
b
b
, а
интеграл
∫
∞
1
2cos
2
1
dx
x
x
сходится (см. предыдущий пример). Следовательно, интеграл
расходится.
∫
∞
1
|cos|
dx
x
x

Упражнения
Найти несобственные интегралы или установить их расходимость:
2.4.1.1.
∫
∞
1
x
dx
. 2.4.1.2.
∫
∞
1
2
x
dx
.
2.4.1.3.
∫
∞
1
x
dx
. 2.4.1.4.
∫
∞
∞−
+
2
1
2
x
xdx
.
2.4.1.5.
∫
∞
∞−
++ 52
2
xx
dx
. 2.4.1.6.
∫
∞
−
1
2
1xx
dx
.
2.4.1.7. .
∫
∞
−
0
2
dxe
x
2.4.1.8. .
∫
∞
0
sin xdxx
2.4.1.9.
∫
∞
−
0
dxe
x
.
2.4.1.10.
∫
∞
+
1
2
1
arctg
x
xdx
.
2.4.1.11. .
∫
∞
−
0
3
dxe
x
2.4.1.12. .
∫
∞
−
0
3
dxxe
x
2.4.1.13. Дайте определение несобственного интеграла с бесконечным верхним пределом
интегрирования. Сходится ли интеграл
? Ответ обоснуйте.
∫
∞
0
cos xdx
2.4.1.14. Дайте определение несобственного интеграла с бесконечным нижним пределом
интегрирования. Сходится ли интеграл
? Ответ обоснуйте.
∫
∞−
0
dxe
x
2.4.1.15. Дайте определение несобственного интеграла с бесконечными пределами интегрирования.
Приведите примеры.
2.4.1.16. При каких положительных значениях α несобственный интеграл
∫
∞
1
α
x
dx
сходится, а при каких
расходится? Ответ обоснуйте.
2°. Несобственные интегралы от неограниченных функций
Если функция f (х) определена при а ≤ х < b, интегрируема на любом отрезке [а, b − ε], 0 < ε < b − а и
не ограничена слева от точки
b, то по определению полагают
()
∫
b
a
dxxf = .
()
∫
−
+→
ε
ε
b
a
dxxf
00
lim
Если этот предел существует и конечен, то несобственный интеграл называется
сходящимся. В
противном случае интеграл называется
расходящимся.
Аналогично, если функция не ограничена справа от точки а, то
()
xf
()
∫
b
a
dxxf = .
()
∫
+
+→
b
a
dxxf
ε
ε
00
lim
Наконец, если функция в окрестности внутренней точки
с отрезка
[
]
ba, не ограничена, то по
определению
()
∫
b
a
dxxf = + .
()
∫
с
a
dxxf
()
∫
b
с
dxxf
Пусть функция
непрерывна на отрезке
()
xf
[
]
ba, , за исключением конечного числа точек. Если
существует функция
, непрерывная на
()
xF
[
]
ba, , для которой
(
)
=
′
xF
(
)
xf, кроме конечного числа точек,
то имеет место формула Ньютона–Лейбница:
()
∫
b
a
dxxf =
(
)
(
)
bFaF
−
.
Функция
F (x) иногда называется обобщенной первообразной для функции на отрезке
()
xf
[
]
ba, .
Для функций, определенных и положительных на промежутке
bxa
<
≤
, справедливы признаки
сходимости (признаки сравнения), аналогичные признакам сравнения для несобственных интегралов с
бесконечными пределами.
