Бабайцев В.А.,Браилов А.В.,Винюков И.А.,Рябов П.Е. Учебник по Высшей математике
Подождите немного. Документ загружается.


1.2.11. Cxxx ++− tg tg
3
1
3
. 1.2.12. Cxx ++ tgln tg
2
1
2
.
1.2.13. Cxxx +−+
2
4
2
1
2
1
arcsin2 .
1.2.14. Cxxx ++−− arcsin
2
1
1
2
1
2
.
1.2.15. Cxx +−−+ ln11ln
2
. 1.2.16. Cxe
x
+−−+ 11ln2 .
1.2.17. xxxx sinsinsin
5
3
sin
7
1
357
+−+− C+ .
1.2.18. xxx coscos
3
2
cos
5
1
35
−+− C+ .
§ 1.3. Интегрирование по частям
1.3.1. . Cexeex
xxx
++− 22
2
1.3.2. . Cxxxxxxx +−−+ cos6sin6cos3sin
23
1.3.3. C
x
xx
+− 2
2ln
1
2
2ln
2
.
1.3.4.
(
)
Cxxx
+
+
cosln tg .
1.3.5. Cxxx +− 4ln2 .
1.3.6. Cxxxx +−+
2
1
arctg
2
1
arctg
2
1
2
.
1.3.7. Cxxx ++−− 2arcsin12 . 1.3.8. . Cxe
x
+cos
1.3.9. Cxxxx +++++ 4ln24
2
1
22
.
1.3.10. Cxxx +−−− 11 arctg .
1.3.11.
(
)
Cxxe
x
+−+
2arcsin
1
2
1
.
1.3.12. Cxxxxx ++−
3323
27
2
ln
9
2
ln
3
1
.
1.3.13. C
x
x
x +
+
+
12
1
arctg
2
1
2
.
1.3.14.
() ()()
Cxxx +− lncoslnsin
2
1
.
1.3.15. .
()
x
exx 723
2
+− C+
1.3.16. .
()
xxxxx cos)56(sin153
2
++−+ C+
1.3.17. .
()
xxxxx cos)433(sin36
2
−+−+ C+
1.3.18. )1ln3(
9
1
3
−xxC+ . 1.3.19.
(
)
x
exx 723
2
+− C
+
.
1.3.20. .
()
xxxxx cos)56(sin153
2
++−+ C+
1.3.21. .
()
xxxxx cos)433(sin36
2
−+−+ C+
1.3.22. )1ln3(
9
1
3
−xx C+ .
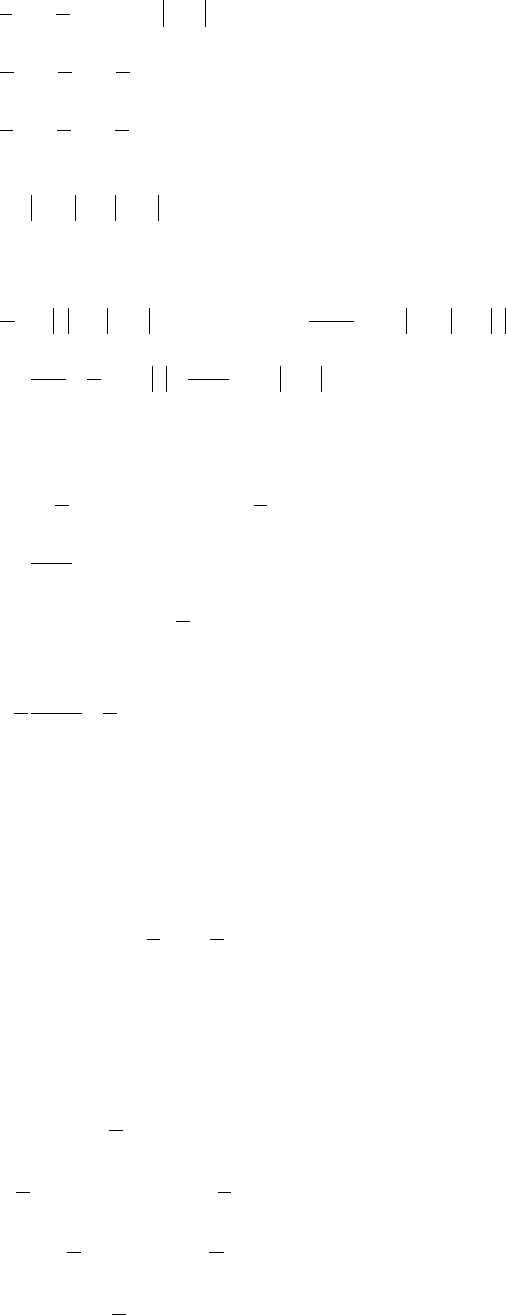
§ 1.4. Интегрирование некоторых классов функций
1
°. Интегрирование рациональных функций
1.4.1.1. Cxxxx +−+++ 1ln
2
1
3
1
23
.
1.4.1.2.
()
Cxxx +++− 1ln
2
1
2
1
4
1
224
.
1.4.1.3. Cxxx ++−
226
arctg
2
1
2
1
6
1
.
1.4.1.4.
() ( )
Cxx
+
−++ 4ln21ln3 .
1.4.1.5. Cxx +−−+ 3ln8ln2 .
1.4.1.6. .
() ()
Cxxx +++−+− 2ln92ln3ln
1.4.1.7.
() () ( )( )
Cxxxx
+
+
−−
+
−−+ 2ln2ln31ln21ln .
1.4.1.8. Cxx
x
+−+− 1lnln
1
. 1.4.1.9. Cxx
x
+−−+
−
ln2ln2
2
3
.
1.4.1.10. Cx
x
x
xx
+−−
−
−+−− 1ln3
1
1
ln3
2
2
1
2
.
1.4.1.11. .
()
()
Cxxx +++++ 1 arctg 322ln2
2
1.4.1.12. .
()
()
Cxx ++++ 4ln31ln
2
1.4.1.13.
()
Cxx
x
x +−+−−
2
1
arctg 4ln2
3
22
.
1.4.1.14.
()
()
Cxx
x
++−++
+
− 1ln1ln2
1
2
2
.
1.4.1.15.
() ()
Cxxxx ++++−+ arctg 1ln2
2
1
arctg 4ln3
22
.
1.4.1.16. . |4|ln5
23
−+++ xxxxC+
1.4.1.17. Cx
x
x
++
+
−
arctg
2
1
1
2
2
1
2
.
1.4.1.18. .
()
()
Cxxx ++−++ 1 arctg 102ln
2
1.4.1.19. . xxxx arctg3
23
+++ C+
1.4.1.20. . )5ln()2ln(3 −++ xxC+
1.4.1.21. . )3arctg(2)106ln(
2
++++ xxxC+
1.4.1.22. . |5|ln45
23
−+++ xxxxC+
1.4.1.23. xxxx
4
1
arctg
4
1
33
23
+++ C+ .
1.4.1.24. . )4ln(4)5ln( −++ xxC+
1.4.1.25. . )5arctg(2)2610ln(4
2
++−+ xxxC+
2°. Интегрирование тригонометрических выражений
1.4.2.1.
C
x
+
+
2
tg1 arctg
.
1.4.2.2.
()()
Cxxxx ++−+−−− 2cossinln
4
1
2cossinln
4
1
.
1.4.2.3.
C
xx
+
−+
+− 1
2
tg2ln2
2
tgln
.
1.4.2.4.
()
()
Cxx ++−+
2
tg1ln
2
1
tg1ln .

1.4.2.5. Cxx +−− 2cos
4
1
8cos
16
1
.
1.4.2.6. Cxx ++ 3sin
6
1
2sin
4
1
. 1.4.2.7. Cxx +−
35
cos
3
1
cos
5
1
.
1.4.2.8. Cxxx +−+ 2sin
4
1
4sin
32
1
8
3
. 1.4.2.9. Cxx +−−
3
ctg
3
1
ctg .
1.4.2.10. xxxxxxx
624
cossin
7
1
sin
35
2
cossin
35
1
cossin
35
8
+++− C
+
.
1.4.2.11. xx cos
2
1
5cos
10
1
+− C+ .
1.4.2.12. xx 11sin
22
1
sin
2
1
− C
+
.
1.4.2.13. xx 12sin
24
1
4sin
8
1
+ C+ .
1.4.2.14. )ln(cos)sin1ln(cossin
3
1
sin
3
4
2
xxxxx −+++− C
+
.
1.4.2.15. xx cos
2
1
7cos
14
1
−− C+ .
1.4.2.16. xx 15sin
30
1
3sin
6
1
+ C
+
.
§ 1.5. Задачи на разные методы интегрирования
1.5.1.
()
Ceee
xxx
++−−+
2
2
1
622ln4
.
1.5.2.
()
C
xx
+
−
+
−
2ln
12ln
2ln
12
.
1.5.3.
()
(
)
Cxx
x
++−−+
1212
12
1ln61ln6
12
.
1.5.4. C
x
x
x
x
+
+
−
+
−
−
1
1
arctg 2
1
2
.
1.5.5. Cxx +−+
2
1arcsin .
1.5.6. C
x
x
+
+
2
9
9
1
.
1.5.7.
()
C
x
xxx +
−
+−+−
2
1
arcsin2231
2
1
2
.
1.5.8. Cxxxxx ++++++++ 842ln284
22
.
1.5.9. Cxxxxxx +++++++++− 38)4(
2
1
384ln
2
13
22
.
1.5.10.
()
Cxxxxxx +++++++++ 542
2
1
542ln
2
1
22
.
1.5.11. . Ce
x
e
+
1.5.12. . Cexe
xx
+−
1.5.13.
()()
Cee
xx
+−++
−−
1ln
3
1
12ln
6
1
.
1.5.14.
()
Cxx
x
x
++−+−
2
1ln
2
1
ln
arctg
.
1.5.15. Cx
x
++− arctg
2
.
1.5.16. Cxxx +
−
⋅
−
cosln ctg .
1.5.17.
()
()
()
()
Cxxxxxx ++++++−++−− 1 arctg
8
1
22ln
16
1
1 arctg
8
1
22ln
16
1
22
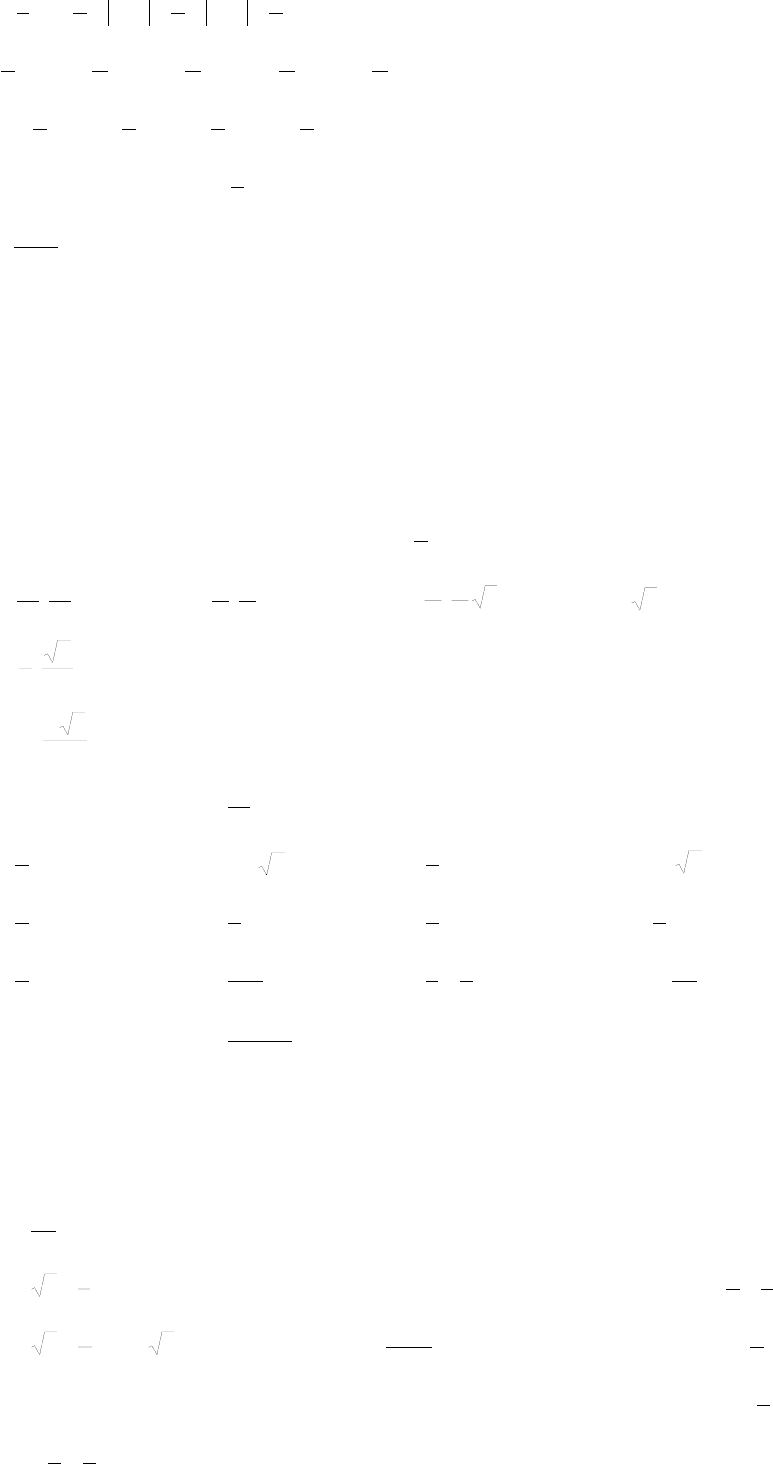
1.5.18. Cxxxx +++−−+ arctg
2
1
1ln
4
1
1ln
4
1
3
1
3
.
1.5.19. Cxxxxx +++−+− ) tg1ln(
2
1
tg
2
1
tg
4
1
tg
6
1
tg
22468
8
1
.
1.5.20. Cxcxxx +++−+− ) tg1ln(
2
1
ctg
2
1
ctg
4
1
ctg
6
1
2246
.
1.5.21.
()
Cxxxx ++−+
2
1
arctg 424ln .
1.5.22.
p
e
p 22 −
.
1.5.23. .
2
p
e
1.5.24. .
()
()
1exp +−
−
pe
p
1.5.25. .
()
ttt 2ln2exp −
Глава 2
Определенный интеграл
§ 2.1. Определение и свойства
2.1.1. 1. 2.1.2. 1.
2.1.3.
2
1
.
2.1.4.
1. 2.1.5. 2.
2.1.6.
13
1
;
14
1
.
2.1.7.
3
;
5
ππ
. 2.1.8.
5
4
;
2
ππ
.
2.1.9.
(
)
3;8.
2.1.10.
2
2
;
2
1
.
2.1.11. .
()
1
;0
−
e
2.1.12.
(
)
π
2;0.
2.1.13.
(
)
4
2;2 e .
2.1.14.
3
3
;0
π
.
2.1.15.
64. 2.1.16. 2. 2.1.17. –2.
2.1.18.
0.
2.1.19.
6
17
.
2.1.20.
55
−
e .
2.1.21.
2.
2.1.22.
3ln
2
1
.
2.1.23.
22 − .
2.1.24.
π
6
1
.
2.1.25.
(
)
12ln + .
2.1.26.
4
7
.
2.1.27.
π
4
1
.
2.1.28.
π
6
1
.
2.1.29.
π
2
1
.
2.1.30.
2
3
. 2.1.31.
35
388
. 2.1.32.
π
4
7
3
8
+ . 2.1.33.
32
21
ln .
2.1.34.
. 2ln2 +
2.1.35.
x
x
2
sin2
§ 2.2. Методы интегрирования
1
°. Замена переменной в определенном интеграле
2.2.1.1.
3
20
.
2.2.1.2. 2ln27
+
. 2.2.1.3.
π
−4.
2.2.1.4.
π
3
1
3 − .
2.2.1.5.
π
.
2.2.1.6.
π
8
1
4
1
+ .
2.2.1.7.
()
32ln
2
1
3 ++ . 2.2.1.8.
5
6156
.
2.2.1.9.
π
2
5
1+ .
2.2.1.10. . xln34 − 2.2.1.11. 3ln2ln2
−
.
2.2.1.12.
π
2
1
2 − .
2.2.1.13.
π
4
1
3
2
+− .
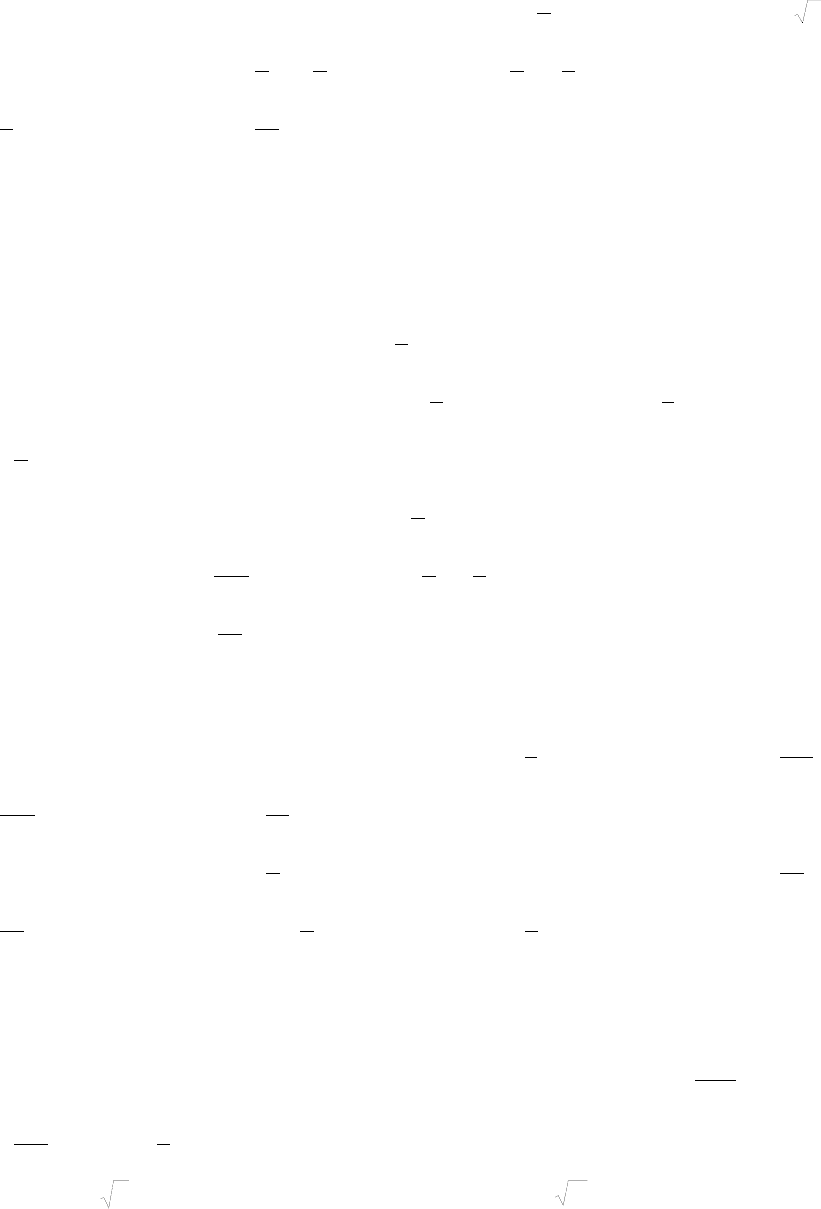
2°. Интегрирование по частям
2.2.2.1. e . 2− 2.2.2.2. 2−
π
.
2.2.2.3.
e
2
1− .
2.2.2.4.
42 −
π
.
2.2.2.5.
1.
2.2.2.6.
2
1
2
1
+
π
e . 2.2.2.7. 2ln
2
1
4
1
−
π
.
2.2.2.8.
1.
2.2.2.9.
6
1
.
2.2.2.10.
π
8
35
.
2.2.2.11. . 94
2
+e
2.2.2.12. 2ln1035
−
+
π
.
§ 2.3. Некоторые приложения определенного интеграла
1
°. Нахождение площадей плоских фигур
2.3.1.1. 9. 2.3.1.2. 27.
2.3.1.3.
2
9
.
2.3.1.4.
π
2. 2.3.1.5. 6ln6.
2.3.1.6.
1. 2.3.1.7. 25,6.
2.3.1.8.
6
1
57 . 2.3.1.9.
8
3
30 .
2.3.1.10. 3
2
9
−
π
.
2.3.1.11.
π
44 +− .
2.3.1.12. 27.
2.3.1.13.
. 2ln86 − 2.3.1.14.
π
.
2.3.1.15.
2ln
2
1
.
2.3.1.16.
1.
2.3.1.17.
6
343
.
2.3.1.18.
3
1
2
1
−
π
.
2.3.1.19.
.
4ln1610 −
2.3.1.20.
3
32
.
2°. Нахождение объемов тел вращения
2.3.2.1.
π
16 . 2.3.2.2.
π
20 .
2.3.2.3.
π
3
8
.
2.3.2.4.
π
5
108
.
2.3.2.5.
π
3
500
.
2.3.2.6.
π
10
3
.
2.3.2.7.
π
12 .
2.3.2.8.
.
2
51
π
2.3.2.9.
.
2
π
2.3.2.10.
3
3
4
r
π
.
2.3.2.11.
π
2.
2.3.2.12.
π
5
24
.
2.3.2.13.
π
3
64
.
2.3.2.14.
2
4
1
ππ
− . 2.3.2.15.
()
1
2
1
2
−e
π
.
2.3.2.16.
π
64 .
3°. Экономические приложения определенного интеграла
2.3.3.1. 24а; 600000. 2.3.3.2. 750000.
2.3.3.3.
9;
1
10
q
q
+
.
2.3.3.4.
()
5822;10001ln
2
1
arctg
100
2
+
+− qqq
π
.
2.3.3.5.
344;164,08,0 ++ yy .
2.3.3.6.
3825;5015
3
4
+t .
2.3.3.7.
1,903; 2,827. 2.3.3.8. 177,5.
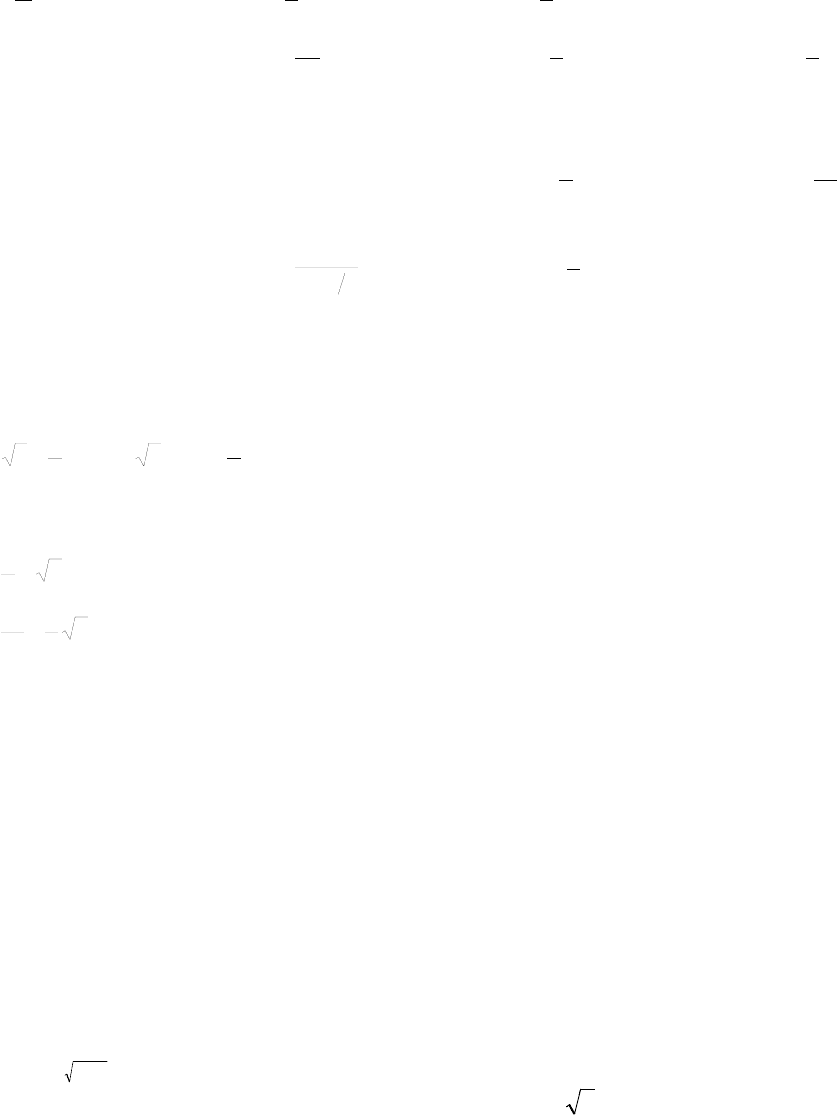
§ 2.4. Несобственные интегралы
1
°. Несобственные интегралы с бесконечными пределами
2.4.1.1. ∞.
2.4.1.2. 1.
2.4.1.3. ∞. 2.4.1.4. ∞.
2.4.1.5.
2
π
. 2.4.1.6.
π
2
1
.
2.4.1.7.
2
1
.
2.4.1.8. Расходится.
2.4.1.9. 2.
2.4.1.10.
2
32
3
π
. 2.4.1.11.
3
1
.
2.4.1.12.
9
1
.
2°. Несобственные интегралы от неограниченных функций
2.4.1.13. –1. 2.4.1.14. Расходится.
2.4.1.15.
π
2
1
.
2.4.1.16.
3
14
.
2.4.1.17. 6.
2.4.1.18. ∞.
2.4.1.19. 4.
2.4.1.20. ∞.
2.4.1.21.
π
.
2.4.1.22.
4sin
π
π
.
2.4.1.23.
9
1
− .
§ 2.5. Численное интегрирование
2.5.1. 2; а) 1,314; б) 1,954; в) 2,001.
2.5.2. ; а) 0,6928; б) 0,6938; в) 0,6932. 6931,02ln =
2.5.3.
()
56,413ln
2
9
1052ln
2
9
5 =+++−− ;
а) 41,49; б) 41,71; в) 41,56.
2.5.4. ; а) 0,6928; б) 0,6938; в) 0,6932. 6931,02ln =
2.5.5. 086,12
2
5
=− ; а) 1,082; б) 1,093; в) 1,086.
2.5.6. 448,32
3
4
3
16
=− ; а) 3,448; б) 3,447; в) 3,448.
2.5.7. ; а) 1,783; б) 1,886; в) 1,843. 803,143ln2 =+−
Глава 3
Двойной интеграл
§ 3.1. Определение двойного интеграла и его свойства
3.1.1. 7/2.
3.1.2.
65 −
π
.
3.1.3.
22. 3.1.4. 93/56.
3.1.5. 63/20. 3.1.6. 24. 3.1.7. 76/3. 3.1.1. 14.
3.1.2. 1/2. 3.1.3. 1/3.
3.1.4. .
∫∫
x
x
dyyxfdx
2
2/
2
0
),(
3.1.5.
∫∫
+1
2
1
0
2
),(
y
y
dxyxfdy .
3.1.6.
3
45,1 .
3.1.7. 2.
§ 3.2. Замена переменных в двойном интеграле
3.2.1. 4sin
π
.
3.2.2.
81/8.
3.2.2.
π
4 .
3.2.4. 2/21
π
.
3.2.5. . 3/)2(ln
3.2.6.
14.
3.2.7. 3 . 10/3)2/1( −arctg
3.2.8.
π
3 .

§ 3.3. Несобственные кратные интегралы
3.3.1. 2/
π
. 3.3.2. 2/
π
.
3.3.3.
3/2
π
.
3.3.4.
Расходится.
3.3.5. Расходится.
3.3.6.
π
.
3.3.7. .
2/32
)1/(18
επε
−−
3.3.8. . 2)2/1( arctg
3.3.9. Расходится.
3.3.10. )147/(2
π
.
3.3.11. Расходится.
3.3.12. . 2/
2
π
3.3.13. Расходится. 3.3.14. 0.
3.3.15. 2.
3.3.16. 4/
π
.
