Бабайцев В.А.,Браилов А.В.,Винюков И.А.,Рябов П.Е. Учебник по Высшей математике
Подождите немного. Документ загружается.

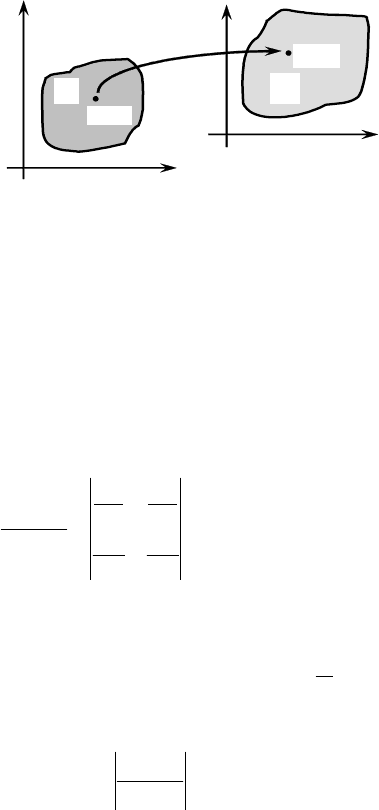
§ 3.2. Замена переменных в двойном интеграле
Пусть имеется множество в плоскости ,Oxy по которому можно интегрировать различные функции
(например, ограниченные и непрерывные). Пусть, далее, имеется другое множество
G
),( yxf
H
в плоскости
по которому также можно интегрировать различные функции. Замена переменных в двойном
интеграле
состоит в переходе к новым переменным и по формулам:
,Ouv
∫∫
G
dxdyyxf ),( u v
(3.6)
∈
=
=
.),(
),,(
),,(
Hvu
vuy
vux
ψ
ϕ
При этом каждой точке ( из G соответствует некоторая точка )( из
, а каждая точка из
)
)
, yx ,vu
H ,( vu
H
переходит в некоторую точку )( множества G (рис. 3.8). ,x y
x
v
0
u
y
(,)uv
(, )xy
G
H
(,)
(,)
xuv
yuv
ϕ
ψ
=
=
0
Рис. 3.8.
Иными словами, когда точка ) "пробегает" множество соответствующая ей точка ,( vu ,H
(
),(),,(),( vuvuyx
)
ψ
ϕ
= "пробегает" множество G . Функции (3.6) называют отображением области
H
плоскости )( на область G плоскости ( ,vu ), y .x
Пусть отображение (3.6) удовлетворяет следующим условиям.
1°. Отображение (3.6) взаимно однозначно, т.е. различным точкам ) из ,( vu
H
соответствуют
различные точки ( из )
)
, yx .G
2°. Функции ,(),,( vuvu
ψ
ϕ
имеют в
H
непрерывные частные производные первого порядка.
3°. Якобиан отображения
vu
vu
vu
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
ψψ
ϕϕ
ψϕ
),(
),(
отличен от нуля во всех точках множества .H
Тогда справедлива теорема о замене переменных в двойном интеграле.
Теорема. Пусть G и
H
– ограниченные, с границей нулевой площади множества, расположенные,
соответственно, в плоскостях и а отображение Oxy ,Ouv
2
,0
π
удовлетворяет условиям 1
°
-3
°
. Тогда
для любой интегрируемой в G функции справедлива формула )y,(xf
∫∫ ∫∫
∂
∂
=
GH
dudv
vu
vuvufdxdyyxf .
),(
),(
)),(),,((),(
ψϕ
ψϕ
(3.7)
Формула (3.7) называется
формулой замены переменных в двойном интеграле.
Замечание. Если условие 1° (взаимная однозначность отображения (3.6)) или условие 3° (отличие от
нуля якобиана отображения) нарушается на множестве точек нулевой площади (например, в отдельных
точках или на отдельных кривых), то формула (3.7) все равно остается справедливой.
Наиболее типичные примеры применения замены переменной для вычисления двойного интеграла
связаны с переходом от прямоугольных координат
x
, на плоскости к полярным координатам .y ,
ϕ
r
В
этом случае:
, (3.8)
∫∫
G
dxdyyxf ),(
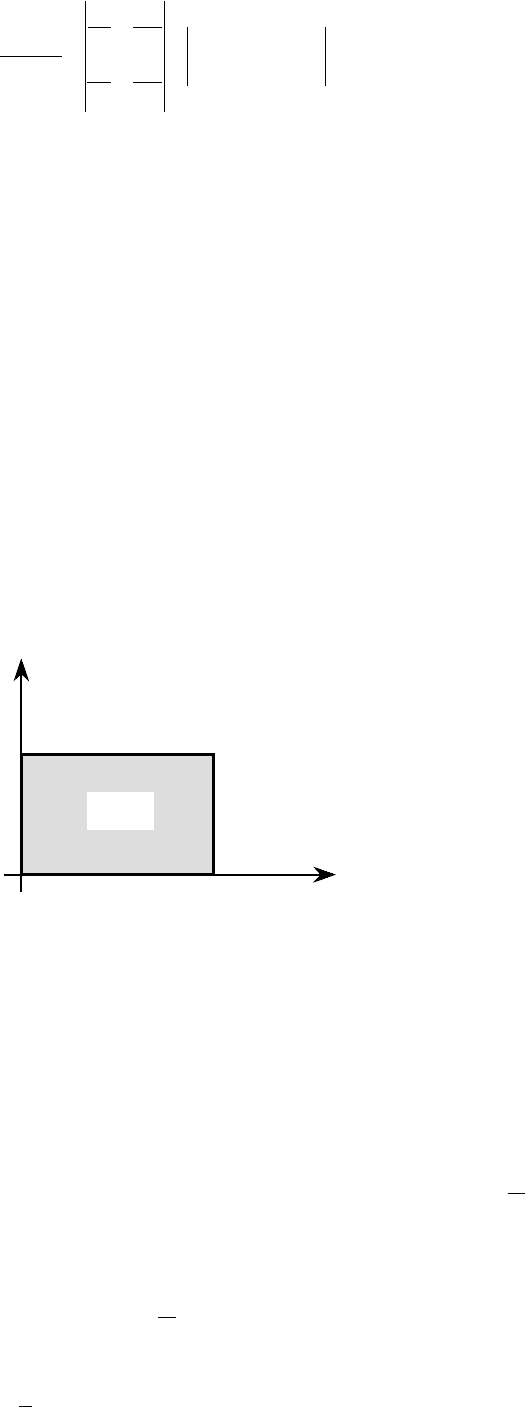
,
cossin
sincos
),(
),(
r
r
r
y
r
y
x
r
x
r
yx
=
−
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
ϕϕ
ϕϕ
ϕ
ϕ
ϕ
следовательно, формула преобразования интеграла приобретает вид:
∫∫ ∫∫
⋅
=
GH
rdrdrrfdxdyyxf .)sin,cos(),(
ϕ
ϕ
ϕ
(3.9)
Формула (3.9) остается в силе и в том случае, если взаимная однозначность соответствия между и G
H
нарушается на некоторых подмножествах в G и
H
нулевой площади (см. замечание).
Например, если – круг ,
а
G
222
Ryx ≤+
H
– прямоугольник ,20,0
π
ϕ
≤≤
≤
≤
Rr то соответствие
(3.8) между и G
H
не является взаимно однозначным, поскольку стороне
H
, примыкающей к оси
ϕ
O
(рис. 3.9), соответствует единственная точка – центр круга . В то же время, если – проколотый круг
а
G G
′
,
2
R
0
22
yx ≤+<
/
H
– полуоткрытый прямоугольник ,20,0
π
ϕ
<
≤
≤
<
Rr то соответствие (3.8) между
и
/
G
/
H
взаимно однозначно. Имеем
∫∫
∫∫ ∫∫ ∫∫
ϕ⋅ϕϕ=
=ϕ⋅ϕϕ==
H
GG H
rdrdrrf
rdrdrrfdxdyyxfdxdyyxf
.)sin,cos(
)sin,cos(),(),(
//
Для площади )(G
σ
круга G получаем знакомую формулу
∫∫ ∫∫ ∫ ∫∫
=====
GH
RR
RrdrrdrdrdrddxdyG
00
2
2
0
.2)(
ππϕϕσ
π
2
π
ϕ
R
r
H
Рис. 3.9
Примеры
1. Вычислить двойной интеграл, переходя к полярным координатам где
∫∫
G
xdxdy,
{}
.0,42:),(
22
≥≤+≤= yxyxxyxG
Решение. Изобразим множество (рис. 3.10) и перейдем к полярным координатам по формулам
(3.8). Подставим формулы (3.8) в уравнения окружностей
и найдем
G
xyxxyx 4,2
2222
=+=+
.cos4,cos2
21
ϕ
ϕ
== rr Следовательно, при каждом значении
ϕ
из промежутка
2
,0
π
переменная
r
изменяется от
ϕ
cos2
1
=r до .cos4
2
ϕ
=r Таким образом, множеству при отображении (3.8)
соответствует более простое множество
G
≤≤≤≤=
ϕϕ
π
ϕϕ
cos4cos2,
2
0:),( rrH
на плоскости ).,( r
ϕ
Имеем
∫∫ ∫∫ ∫ ∫
=
=⋅=
GH
drrdrdrdrxdxdy
2
0
cos4
cos2
2
coscos
π
ϕ
ϕ
ϕϕϕϕ

=
∫∫
==
2
0
2
0
4
cos4
cos2
3
.
2
7
cos
3
56
cos
3
ππ
ϕ
ϕ
π
ϕϕϕϕ
dd
r
При вычислении последнего интеграла два раза воспользовались формулой понижения степени
.
2
2cos1
cos
2
ϕ
ϕ
+
=
2
π
x
r
y
ϕ
ϕ
r
0
0
G
2 4
2
4
H
Рис. 3.10.
Иногда удобно перейти к обобщенным полярным координатам, которые определяются по формулам
β
(3.10)
=
=
,sin
,cos
ϕ
ϕ
α
bry
arx
где
β
α
,,, ba – некоторые числа, выбираемые в каждом конкретном случае из соображений удобства.
Якобиан отображения (3.10) равен
=
−
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
−
−
ϕβϕ
ϕϕαϕ
ϕ
ϕ
ϕ
ββ
αε
cossinsin
sincoscos
),(
),(
1
1
rbb
raa
y
r
y
x
r
x
r
yx
.sincos
11
ϕϕ
βα
−−
= abr
2. Вычислить площадь фигуры, ограниченной эллипсом
.1
2
2
2
2
=+
b
y
a
x
Решение. Требуется найти двойной интеграл
∫∫
=
G
dxdyG ,)(
σ
где .10:),(
2
2
2
2
≤+≤=
b
y
a
x
yxG
Поскольку фигура симметрична относительно начала координат и координатных осей, то достаточно найти
площадь
G (рис. 3.11).
(
0,0
1
≥≥∩= yxG
)
b
1
r
y
ϕ
ϕ
r
a
x
1
G
0
0
H
2
π
Рис. 3.11
Для этого перейдем к новым переменным
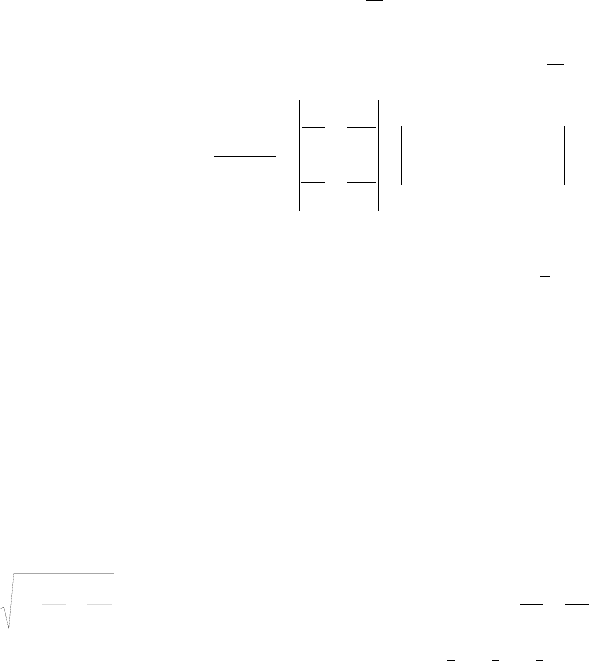
(3.11)
=
=
.sin
,cos
ϕ
ϕ
bry
arx
Подставляя выражения (3.11) в уравнение эллипса, получим ,
откуда ,
1
2
=r 1
=
r причем наглядно видно,
что при каждом значении
ϕ
из промежутка
2
,0
π
переменная
r
изменяется от 0 до 1. Таким образом, на
плоскости )( ,
ϕ
r выделяется множество
.0,10:),(
≤≤=
ϕ
rrH
2
≤≤
π
ϕ
Якобиан отображения
.
cossin
sincos
),(
),(
abr
brb
ara
y
r
y
x
r
x
r
yx
=
−
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
ϕϕ
ϕϕ
ϕ
ϕ
ϕ
Следовательно,
∫∫ ∫∫ ∫∫ ∫ ∫
=
====
GG H
abrdrdababrdrddxdydxdyG
1
2
0
1
0
.444)(
π
πϕϕσ
Таким образом, площадь фигуры, ограниченная эллипсом с полуосями
a и , равна b ab
π
.
Упражнения
Переходя к (обобщенным) полярным координатам, вычислить интегралы.
3.2.1. где G
()
∫∫
+
G
dxdyyx ,cos
22
{}
.4:),(
22
≤+= yxyx
3.2.2.
где G
∫∫
G
xydxdy,
{}
.0,0,9:),(
22
≥≥≤+= yxyxyx
3.2.3.
∫∫
−−
G
dxdy
yx
,
94
1
22
где область ограничена эллипсом G .1
94
22
=+
yx
3.2.4.
где область ограничена астроидой
∫∫
G
dxdyx ,
2
G .4
3
2
3
2
3
2
=+ yx
Произведя надлежащую замену переменных, найти площадь, ограниченную следующими кривыми:
3.2.5. .2,,2,1
22
xyxyxyxy ====
3.2.6.
.2,,4,2
22
xyxyyxyx ====
3.2.7.
.2,,4,2
2222
yxyxyyxyyx ===+=+
3.2.8.
.9)22()12(
22
=−++−+ yxyx
§ 3.3. Несобственные кратные интегралы
Oграничимся рассмотрением лишь двойных несобственных интегралов от ограниченной функции по
неограниченной области. Напомним, что множество
называется ограниченным, если оно целиком
содержится в некотором круге.
2
R⊂G
Определение. Исчерпанием множества называют такую последовательность ограниченных
множеств что
2
R⊆G
{}
,
n
G
1) для любого площадь границы множества G равна 0; N∈n
n
2)
при любом n (условие монотонности);
1+
⊂
nn
GG
3)
.
1
n
n
GG
∞
=
∪=
Примеры
1. Для любого зададим круг неравенством . Последовательность кругов N∈n
n
G
222
nyx <+
{
}
n
G
является исчерпанием плоскости
2
R
, так как условия 1) – 3) выполняются очевидным образом.
2. Для любого неравенствами N∈n nynn
x
n
<
<
−
<
<
−
,
2
зададим квадрат . Семейство квадратов
также является исчерпанием плоскости
n
G
{}
n
G
R
.
Определение. Пусть – неограниченное множество; –функция, интегрируемая по
любому ограниченному с границей нулевой площади подмножеству в G. Предположим, что для любого
исчерпания
{
множества G предел
2
R⊂G ),( yxf
}
n
G
(3.12)
∫∫
∞→
=
n
G
n
dxdyyxfI ),(lim
существует и не зависит от выбора исчерпания. Тогда предел
I
обозначается и
называется
несобственным двойным интегралом от функции по множеству G .
∫∫
G
dxdyyxf ),(
f
Таким образом, несобственный интеграл является пределом собственного интеграла и, как и всякий
предел, может быть равным или ∞+
∞
− или же быть числом. В последнем случае говорят, что
несобственный интеграл сходится. Если же несобственный интеграл не является числом, то говорят, что он
расходится. Несобственный интеграл расходится и в тех случаях, когда, несмотря на интегрируемость
по любой конечной части , предел (3.12) не существует для какого-либо исчерпания ),( yxf G
{
}
n
G или
существует, но зависит от
{}
.
n
G
Проверку сходимости несобственного интеграла от неотрицательной функции облегчает следующая
теорема.
Теорема. Если функция – неотрицательна на множестве G и хотя бы для одного исчерпания
множества существует предел , то несобственный интеграл
сходится.
),( yxf
{}
n
G G
∫∫
∞→
n
G
n
dxdyyxf ),(lim
∫∫
G
dxdyyxf ),(
3. Доказать сходимость интеграла и найти его значение.
∫∫
+−
=
2
R
dxdyeI
yx )(
22
Решение. Подынтегральная функция
положительна. Рассмотрим
последовательность множеств
исчерпывающую
)(
22
),(
yx
eyxf
+−
=
}
,,2,1, K=n
{
:),(
222
<+= nyxyxG
n
2
R
. Переходя к
полярным координатам
=
=
,sin
,cos
ϕ
ϕ
ry
rx
находим
r
r
r
y
r
y
x
r
x
r
yx
=
−
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
ϕϕ
ϕϕ
ϕ
ϕ
ϕ
cossin
sincos
),(
),(
.
Следовательно,
(
)
∫∫ ∫ ∫∫
−−−+−
−==
==
n
G
n
nr
n
ryx
n
erdrerdreddxdyeI
π
ππϕ
2
000
)(
.12
22222
Отсюда,
.lim
π
=
=
∞→
n
n
II
В силу сформулированной выше теоремы, таков же будет предел и для любой другой последовательности
множеств, исчерпывающей
2
R
. Поэтому интеграл сходится и равен
∫∫
+−
=
2
R
dxdyeI
yx )(
22
π
.

4. Вычислить интеграл
∫
+∞
∞−
−
.
2
dxe
x
Решение.
Возьмем последовательность квадратов
{
,,:),( nynnxnyxG
n
}
<
<−<<−= где , исчерпывающую ,2,1 K=n
2
R
. В условиях предыдущего примера
имеем
=
⋅
==
∫∫∫∫
−
−
−
−
∞→
+−
∞→
n
n
y
n
n
x
G
n
yx
n
eedxdyeI
n
2222
limlim
)(
.lim
22
22
=
=
∫∫
∞+
∞−
−
−
−
∞→
dxee
x
n
n
x
n
Отсюда,
∫
+∞
∞−
−
= .
2
π
dxe
x
5. Найти несобственный интеграл
.
)1)(1(
||
22
∫∫
≤
++
xy
yx
dxdy
Решение. Рассмотрим исчерпание плоскости
2
R
квадратами
{
}
,,:),( nynnxnyxG
n
<
<
−
<<−
=
где
Нетрудно видеть, что пересечение области интегрирования K,2,1=n G∩GG
nn
=
/
{}
xyyxG
≤
= |:|),( с
квадратом
задается неравенствами
n
G nxy
<
≤
|| и определяет исчерпание
{
}
/
n
G области интегрирования
. Следовательно, G
∫∫∫∫
<≤≤
∞→
=
++
=
++
nxyxy
n
yx
dxdy
yx
dxdy
||
22
||
22
)1)(1(
lim
)1)(1(
∫∫ ∫
−
=
−=
∞→∞→
=
+
=
++
=
xx
x
n
xy
xy
nn
dx
x
y
yx
dy
dx
00
222
)1(
arctg
lim
)1)(1(
lim
∫
==
+
=
∞→∞→
n
n
nn
xdx
x
x
0
2
0
2
2
.
4
arctg lim
)1(
arctg2
lim
π
Признак сравнения. Пусть и – функции такие, что ),( yxf ),( yxg ),(),(0 yxgyxf
≤
≤
∫∫
G
dxdyyxg ),(
∫∫
G
dxdyyxf ),(
на
неограниченном множестве G. Тогда из сходимости несобственного интеграла следует
сходимость несобственного интеграла
а из расходимости интеграла следует
расходимость интеграла
∫∫
G
f (
dxdy.(
dxdy,)yx,
∫∫
G
yg )x,
Теорема. Пусть – неограниченное множество, – функция, определенная на и
интегрируемая по всякому подмножеству в с границей нулевой площади. Тогда из сходимости
интеграла
вытекает сходимость интеграла
2
R⊂G
dxdy
),( yxf
yxf ),(
G
G
∫∫
G
yxf |),(|
∫∫
G
dxdy.
Замечание. Если сходимость несобственного интеграла устанавливается как следствие
сходимости интеграла
то говорят, что интеграл сходится абсолютно.
∫∫
G
dxdyyxf ),(
∫∫
G
dxdyyxf ),(
∫∫
G
dxdyyxf ,|),(|
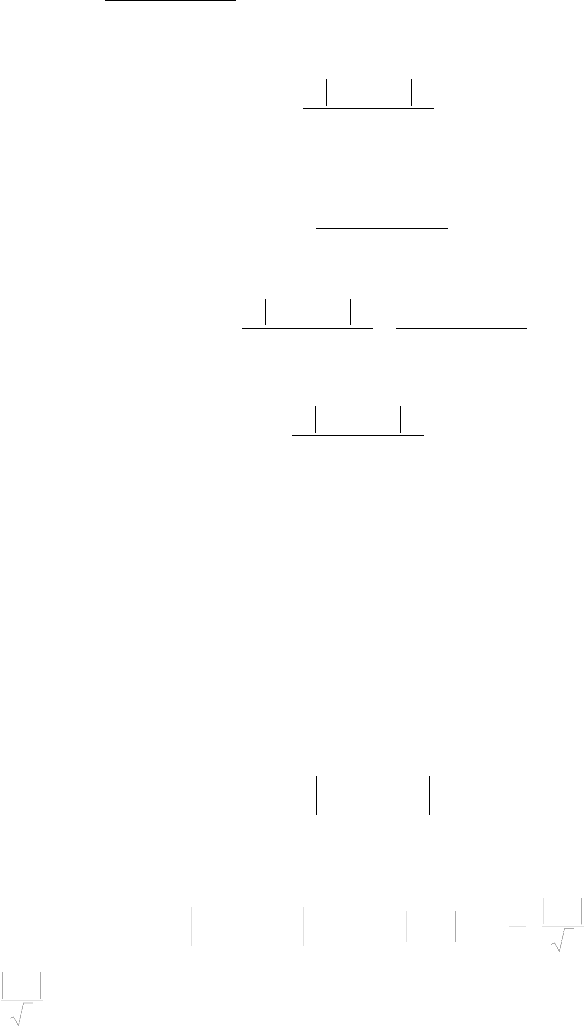
6. Доказать сходимость несобственного интеграла
∫∫
≤
++
xy
dxdy
yx
yx
||
22
.
)1)(1(
sinsin
(3.13)
Решение. Действительно, функция
)1)(1(
sinsin
22
yx
yx
++
непрерывна и, следовательно, интегрируема по любому ограниченному множеству с границей нулевой
площади. С учетом сходимости интеграла
∫∫
≤
++
xy
yx
dxdy
||
22
)1)(1(
из неравенств
)1)(1(
1
)1)(1(
sinsin
0
2222
yxyx
yx
++
≤
++
≤
по признаку сравнения получаем сходимость интеграла
∫∫
≤
++
xy
dxdy
yx
yx
||
22
.
)1)(1(
sinsin
Отсюда по предыдущей теореме вытекает сходимость интеграла (3.13).
Теорема. Если кратный интеграл сходится, то сходится и интеграл
∫∫
G
dxdyyxf ),(
∫∫
G
dxdyyxf .|),(|
Смысл этой теоремы в том, что в -мерном ) пространстве понятие сходимости и абсолютной
сходимости несобственного кратного интеграла совпадают, т.е. отсутствует понятие условной сходимости,
в отличие от теории несобственного интеграла от функции одной переменной.
n 2( ≥n
7. Доказать, что интеграл
(
)
∫∫
+=
2
R
dxdyyxI
2
22
sin
расходится.
Решение. Исследуем на сходимость интеграл
(
)
∫∫
+=
2
R
,sin
2
22
1
dxdyyxI
в котором подынтегральная функция неотрицательна. Пусть
{}
K,2,1,:),(
222
=≤+= nnyxyxG
n
– исчерпание плоскости R
2
, тогда
()
∫∫ ∫ ∫
==+=
n
G
nn
n
dt
t
t
rdrrdxdyyxI
00
4
2
22
1
2
.
sin
2
sin2sin
π
π
Но интеграл
∫
∞
0
sin
dt
t
t
расходится и стремится к
∞
+
(см. соответствующий пример из главы 2), поэтому
и, значит, интеграл расходится. Если бы данный интеграл ,lim
1
+∞=
∞→
n
n
I
1
I
I
сходился, то, согласно
предыдущей теореме, сходился бы и интеграл .
Значит, из его расходимости следует расходимость
интеграла
1
I
(
sin
22
+ yx
)
.
2
dxdy
∫∫
2
R
Для вычисления несобственных интегралов, так же как и для собственных, используется прием
сведения кратного интеграла к повторному интегралу. Несобственным аналогом (3.5), является формула
() ()
∫∫ ∫ ∫
∞
∞−
∞
∞−
=
2
,,
R
dxdyyxfdxdyyxf ,
которая записывается обычно без внутренних фигурных скобок в виде
. (3.14)
() ()
∫∫ ∫ ∫
∞
∞−
∞
∞−
=
2
,,
R
dyyxfdxdxdyyxf
Равенство (3.14) выполняется при условии абсолютной сходимости повторного интеграла в правой
части:

. (3.15)
()
+∞<
∫∫
∞
∞−
∞
∞−
dyyxfdx |,|
Дополнительное условие (3.15) связано с тем, что сходимость несобственного однократного
интеграла, в отличие от двойного, не означает его абсолютной сходимости.
8. Найти несобственный интеграл
()
∫∫
+
++
2
3
1
R
yx
dxdy
,
где
задается неравенствами .
2
+
R 0,0 ≥≥ yx
Решение. Мы не можем непосредственно применить (3.14), поскольку область интегрирования
отлична от
2
R
. Тем не менее, можно воспользоваться стандартным приемом – расширить область
интегрирования до
2
R
, положив подынтегральную функцию равной 0 вне исходной области
интегрирования. В результате получим
() () ()
=
++
−=
++
=
++
∫∫∫∫∫
∞
∞=
=
∞∞
+
0
0
2
0
3
0
3
12
1
11
2
dx
yxyx
dy
dx
yx
dxdy
y
y
R
()
()
2
1
12
1
12
0
0
2
=
+
−=
+
=
∞
∞
∫
x
x
dx
.
9. Найти несобственный интеграл
(
)
∫∫
+
+−
2
cos
R
dxdyxe
yx
. (3.16)
Решение. Данный интеграл легко сводится к повторному
.
() ()
∫∫∫∫∫∫
∞
−
∞
−
∞
+−
∞
+−
⋅==
+
0000
coscoscos
2
ydyedxeydyedxdxdyye
yxyxyx
R
Вычислив предварительно неопределенные интегралы
()
CyyeydyeCedxe
yyxx
+−=+−=
−−−−
∫∫
cossin
2
1
cos,,
найдем несобственный интеграл (3.16)
()
()
2
1
cossin
2
1
cos
0
0
00
=
−⋅−=⋅
∞
−
∞
−
∞
−
∞
−
∫∫
yyeeydyedxe
yxyx
.
Поскольку подынтегральная функция знакопеременная, решение будет не полным, если не проверить
условие (3.15) абсолютной сходимости повторного интеграла:
() ()
+∞<==≤
∫∫∫∫∫∫
∞
−
∞
−
∞
+−
∞∞
+−
∞
1|cos|
000000
dyedxedyedxdyyedx
yxyxyx
.
Упражнения
Вычислить несобственный интеграл или установить его расходимость.
3.3.1.
()
∫∫
+
+−
2
R
.cos
22)(
22
dxdyyxe
yx
3.3.2.
()
∫∫
+
+−
2
R
.sin
22)(
22
dxdyyxe
yx
3.3.3.
∫∫
++−
2
R
.
)(
22
dxdye
yxyx
3.3.4.
()
∫∫
+
2
R
.sin
44
dxdyyx
3.3.5.
∫∫
≥+
+
1
222
22
.)(sin
yx
xddyyx
3.3.6.
()
∫∫
>+
+
1
2
22
22
.
yx
yx
dxdy

3.3.7.
∫∫
++−
2
R
,
934
22
dxdyxye
yxyx
ε
где
()
.1,1−∈
ε
3.3.8.
где
()
∫∫
−
G
yx
dxdyxye ,2sin
2
{}
.0,1:),( >>= yxyxG
3.3.9.
где
()
∫∫
−
G
xy
dxdyxye ,2sin
{}
.0,1:),( >>= yxyxG
3.3.10.
∫∫
+−
2
22
.)3cos()2cos(
R
dxdyyxe
yx
3.3.11.
()
∫∫
+
2
R
.sin
22
dxdyyx
3.3.12.
∫∫
++
G
yxy
ydxdy
,
))(1(
222
где
{}
.,0:),(
+
∞
<
<
−
∞>= xyyxG
3.3.13.
∫∫
+
−
G
dxdy
yx
yx
,
22
где
{}
.0,0,1:),( >>>+
=
yxyxyxG
3.3.14.
∫∫
+
−
G
dxdy
yx
yx
,
44
где
{}
.0,0,1:),( >>>+
=
yxyxyxG
3.3.15.
∫∫
∞∞
−−
+
00
.)( dxdyeyx
yx
3.3.16.
∫∫
∞∞
−−
+
00
22
.)(
22
dxdyeyx
yx
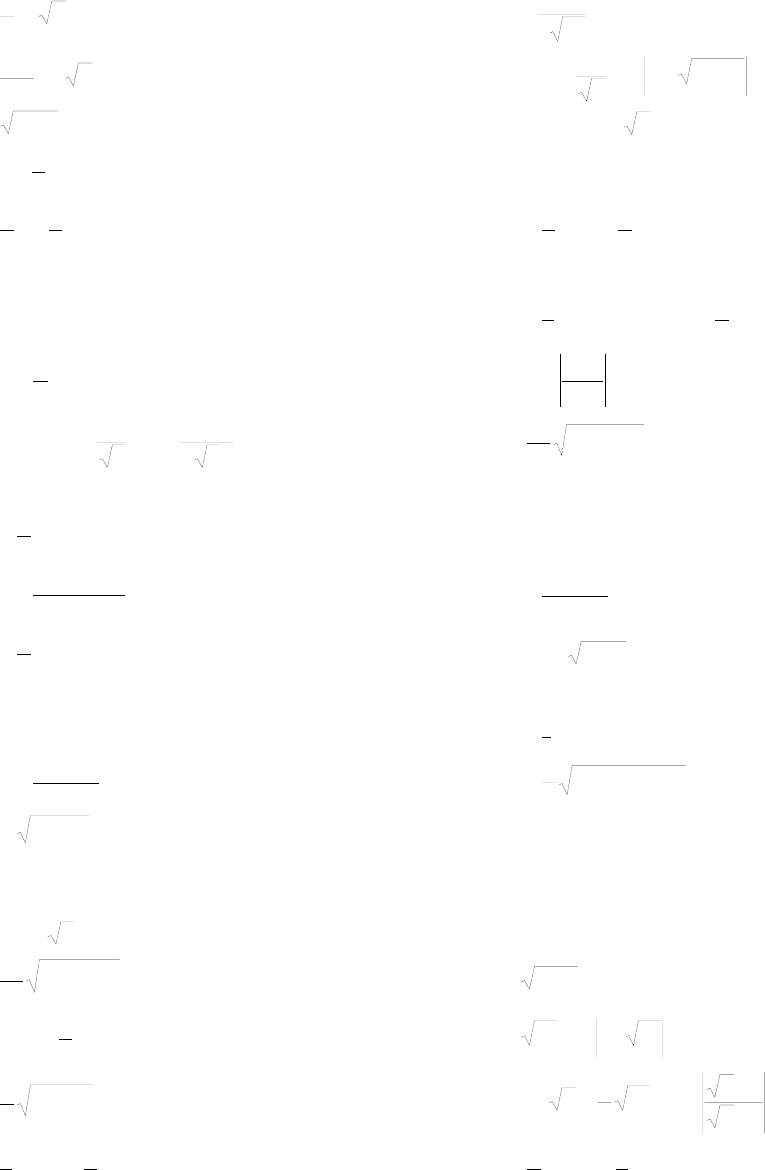
Ответы к упражнениям
Глава 1
Неопределенный интеграл
§ 1.1. Непосредственное интегрирование
1.1.1. Cxxx ++
2
5
2
.
1.1.2. Cxe
x
x
++−− ln
3
2
3
.
1.1.3. Cx
a
a
x
++
3
3
ln
.
1.1.4. Cxx
x
+++− 3ln
3
arcsin
2
.
1.1.5. )395(4 −+ xxC+ .
1.1.6. Cxx ++−
3
3cos2 .
1.1.7. Cxx +− 2cos
2
1
.
1.1.8. Cxx
+
−
−
tg ctg .
1.1.9. Cxx +− sin
2
1
2
1
. 1.1.10. Cxx ++
2
1
sin
2
1
.
1.1.11. . Cxx +−− ctg 1.1.12. Cxx
+
−
tg .
1.1.13. . Cx +− 2 ctg 2
1.1.14. C
x
xx ++−
3
arctg 279
3
1
3
.
1.1.15. Cx
x
++− arctg
1
.
1.1.16.
C
x
x
+
−
+
1
1
ln
.
1.1.17. C
x
x +
+
−
3
12
arctg
3
2
arctg .
1.1.18.
()
Cx ++
5
8
72
16
5
.
1.1.19. .
()
Cxx +−+ 652ln
2
1.1.20.
(
)
Cee
xx
+−
−
ln .
1.1.21. Cx +
2
ln
2
1
.
1.1.22.
(
)
Cx
+
2sinln .
1.1.23. C
x
+−
2
arcsin2
1
.
1.1.24. C
x
+
2
arctg
2
.
1.1.25.
()
Cx +
4
arcsin
4
1
.
1.1.26. Cx +−
3
cos3 .
1.1.27. . Ce
x
+−
cos
1.1.28. Cx
+
|ln|ln .
1.1.29. . Cx +− |1|ln
2
1.1.30.
(
)
12
3
6
1
1 x− C
+
.
1.1.31.
xarcsin
1
− C+ .
1.1.32.
3
)1І(3
3
2
++ xxC+ .
1.1.33. )143()3( −+ xxC+ .
§ 1.2. Замена переменной
1.2.1. Cx +− cos .
1.2.2.
(
)
Cx
+
lnsin .
1.2.3.
()
Cx ++
3
4
3
31
12
1
.
1.2.4.
(
)
Cxx +−+ 63 .
1.2.5. Cxx +−
3
sin
3
1
sin .
1.2.6. Cxx ++−
4
3
4
3
1ln .
1.2.7.
()
Cxx +−+
3
1
3
2
.
1.2.8. C
x
x
xx +
−
+
+−−
1
1
ln2
3
4
4
4
4
4
3
4
.
1.2.9. Cxxx ++− sinsin
3
2
sin
5
1
35
. 1.2.10. Cxx +−
57
cos
5
1
cos
7
1
.
