Бабайцев В.А.,Браилов А.В.,Винюков И.А.,Рябов П.Е. Учебник по Высшей математике
Подождите немного. Документ загружается.


Упражнения
Найти интегралы, применяя метод интегрирования по частям:
1.3.1. .
∫
dxex
x2
1.3.2. .
∫
xdxx cos
3
1.3.3.
∫
⋅ dxx
x
2.
1.3.4.
∫
dx
x
x
2
cos
.
1.3.5.
∫
dx
x
xln
.
1.3.6. .
∫
xdxxarctg
1.3.7.
∫
−
dx
x
x
1
arcsin
.
1.3.8.
(
)
∫
− dxxxe
x
sincos .
1.3.9.
∫
+ dxx 4
2
.
1.3.10. dxx
∫
−1arctg .
1.3.11. .
∫
dxe
xarcsin
1.3.12. .
∫
xdxx
22
ln
1.3.13.
()
∫
+
3
2
1x
dx
.
1.3.14.
(
)
∫
dxxlnsin .
1.3.15. .
()
∫
++ dxexx
x
543
2
1.3.16.
(
)
∫
++ xdxxx cos553
2
.
1.3.17. .
()
∫
++ xdxxx sin233
2
1.3.18. .
∫
xdxx ln
2
1.3.19. .
()
∫
++ dxexx
x
553
2
1.3.20.
(
)
∫
++ xdxxx cos4
2
.
1.3.21. .
()
∫
++ xdxxx sin254
2
1.3.22.
∫
xdxx ln
3
.
1.3.23. Выведите формулу интегрирования по частям для неопределенного интеграла. Приведите пример.
§ 1.4. Интегрирование некоторых классов функций
1
°. Интегрирование рациональных функций
Рациональной функцией называют функцию вида:
()
()
m
mm
n
nn
bxbxb
axaxa
xQ
xP
+++
+++
=
−
−
K
K
1
10
1
10
.
Будем предполагать, что дробь несократимая, правильная
(n < m) и
. Многочлен Q(x) разлагается на множители следующих двух типов: 1
0
=b
1-й тип − (x − α)
k
, k ≥ 1;
2-й тип − (x
2
+ px + q)
l
, l ≥ 1
(квадратный трехчлен не имеет действительных корней).
В курсе алгебры доказывают теорему о разложении рациональной функции на сумму простейших
дробей. При этом каждому типу множителей соответствуют слагаемые следующего вида:
1-й тип −
() ()
k
k
x
A
x
A
x
A
αα
α
−
+
−
+
−
K
2
21
;
2-й тип −
()()
l
ll
qpxx
CxB
qpxx
CxB
qpxx
CxB
++
+
+
++
+
+
++
+
2
2
2
22
2
11
K ,
где коэффициенты A, B
1
, … можно найти методом неопределенных коэффициентов.
Простейшие дроби всех типов, кроме 4-го (в одном случае), интегрируются ранее рассмотренными
заменами переменных, а для вычисления интегралов вида
()
∫
+
n
ax
dx
22
применяется тригонометрическая подстановка tdtax tg
=
или рекуррентная формула

()
()
() ()
∫∫
−−
+
++
+
−
=
+
])32([
1
1
1
22
1
22
2
22
nnn
ax
dx
т
ax
x
an
ax
dx
.
Примеры
1
.
∫
−1
2
x
dx
.
Знаменатель подынтегральной рациональной функции разлагается на линейные множители x
2
− 1 = (x
− 1)(x + 1), поэтому ищем разложение на простейшие дроби в виде
111
1
21
2
+
+
−
=
− x
A
x
A
x
. Приравнивая
числители слева и справа, получим
1 = A
1
(x + 1) + A
2
(x − 1).
Подставляя x = 1, находим 1 = 2A
1
,
2
1
1
=A . Подставляя x = −1, находим 1 = −2A
2
, так что
2
1
2
−=A .
Тогда
∫∫∫
++−−=
+
−
−
=
−
Cxx
x
dx
x
dx
x
dx
1ln
2
1
1ln
2
1
12
1
12
1
1
2
.
2.
()( )
∫
−+
+
= dx
xx
x
I
21
2
3
2
.
Подынтегральная функция − правильная дробь, поэтому ее разложение на простейшие дроби будем
искать в следующем виде:
()( ) ()()
3
3
2
21
3
2
11
12
21
2
+
+
+
+
+
+
−
=
−+
+
x
B
x
B
x
B
x
A
xx
x
.
Приведя к общему знаменателю и приравняв числители, получим
x
2
+ 2 = A(x + 1)
3
+ B
1
(x − 2)(x + 1)
2
+ B
2
(x − 2)(x + 1) + B
3
(x − 2).
Подставив x = 2, найдем A: 2
2
+ 2 = A ⋅ 3
3
,
9
2
=A .
Подставив x = −1, найдем B
3
: 3 = −3B
3
, B
3
= −1.
Чтобы найти коэффициент B
1
, приравняем коэффициенты при x
3
слева и справа. Слева нет степени x
3
,
поэтому такой коэффициент равен 0, справа коэффициент при x
3
может получиться только из первых двух
слагаемых, так что 0 = A + B
1
, откуда
9
2
1
−=B .
Наконец, чтобы найти коэффициент B
2
, подставим x = 0. Получим
2 = A − 2B
1
− 2B
2
− 2B
3
,
так что
3
1
2
=B . Таким образом, искомое разложение на простейшие дроби имеет следующий вид:
()()()() ()()
323
2
1
1
13
1
19
2
29
2
21
2
+
−
+
+
+
−
−
=
−+
+
xxxxxx
x
.
Поэтому интеграл I находится непосредственно
()()
∫∫∫∫
=
+
−
+
+
+
−
−
=
32
11
3
1
19
2
29
2
x
dx
x
dx
x
dx
x
dx
I
() ()
()()()()
∫∫∫ ∫
=++−+++
+
+
−
−
−
=
−−
3111
3
1
1
1
9
2
2
2
9
2
32
xdxxdx
x
xd
x
xd
()
C
x
x
xx +
+
+
+
−+−−=
2
1
2
1
1
1ln
9
2
2ln
9
2
.
3.
()
()
∫
++
+
= dt
tt
tt
I
11
2
2
57
.
Прежде всего разделим числитель на знаменатель с остатком:
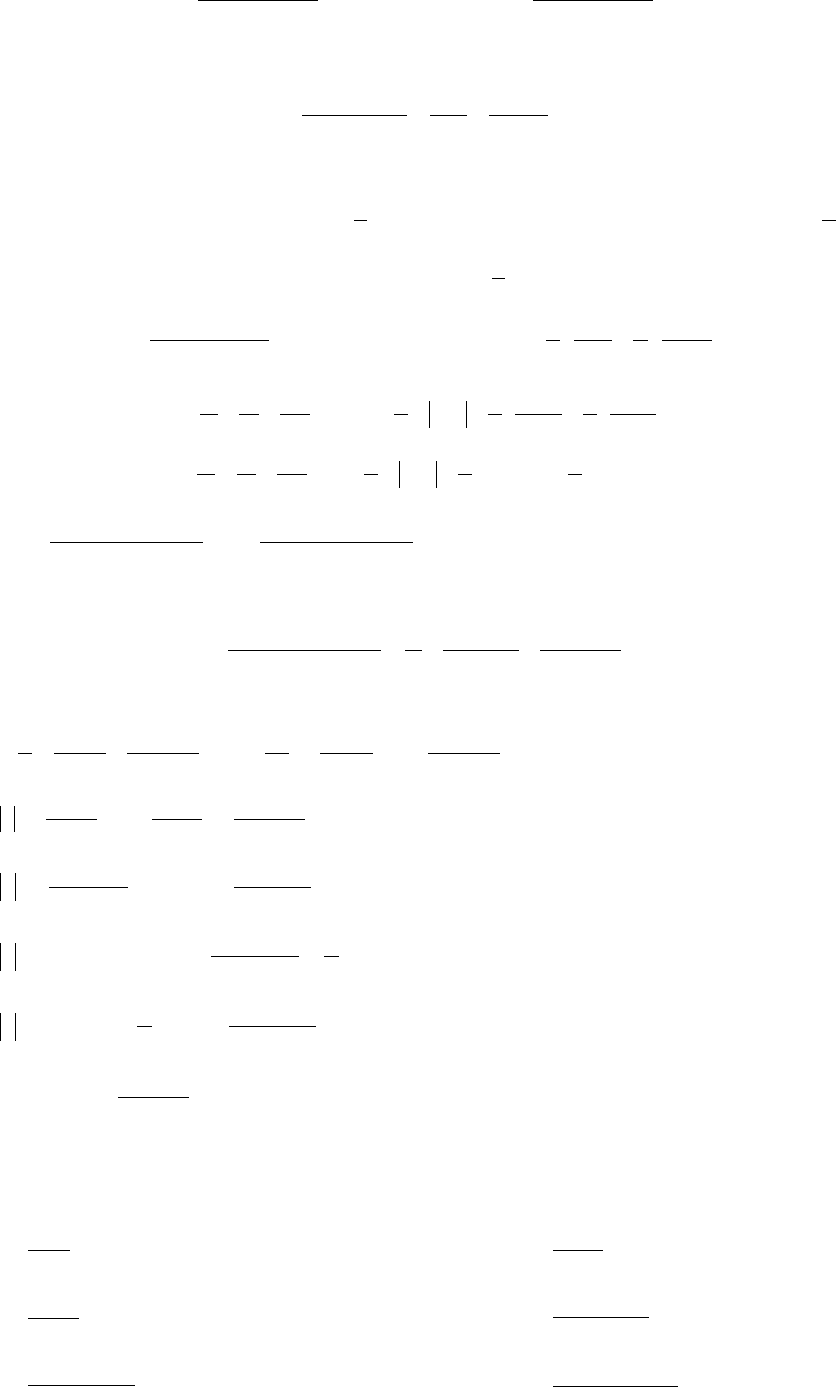
()
()
()
()
11
1
122
11
2
2
2
234
2
57
++
+−
−+−+−=
++
+
tt
tt
tttt
tt
tt
.
Разложим полученную правильную дробь на простейшие:
()
()
1111
1
22
2
+
+
+
+
=
++
+−
t
CBt
t
A
tt
tt
.
t
2
− t + 1 = A(t
2
+ 1) + (Bt + C)(t + 1).
Подставляя t = −1, получим 3 = 2⋅A,
2
3
=A . Подставляя t = 0, найдем C: 1 = A + C,
2
1
−=C . Наконец,
приравнивая коэффициенты при t
2
, получим 1 = A + B,
2
1
−=B . Таким образом,
()
()
()
∫∫∫
=
+
+
+
+
−+−+−=
++
+
= dt
t
t
t
dt
dtttttdt
tt
tt
I
1
1
2
1
12
3
122
11
2
2
234
2
57
∫
=
+
+
+
++−+−+−=
∫∫
12
1
1
2
4
1
1ln
2
3
3
2
45
22
2
345
t
dt
t
tdt
ttt
ttt
()
Ctttt
ttt
+++++−−+−= arctg
2
1
1ln
4
1
1ln
2
3
3
2
45
22
345
.
4.
()
∫∫
+
+++
=
++
+++
= dx
xx
xxx
dx
xxx
xxx
I
2
2
234
35
234
1
143
2
143
.
Представим подынтегральную функцию в следующем виде:
() ()
2
2
22
2
11
2
2
234
1
1
1
143
+
+
+
+
+
+=
+
+++
x
DxC
x
DxC
x
A
xx
xxx
.
Читателю предлагается самостоятельно найти все коэффициенты. Получим:
() ()
∫∫∫
=
+
−
+
+
+=
+
−
+
+
+=
2
2
2
2
2
2
1
1
12
1
1
1
121
x
dx
dx
x
x
x
dx
dx
x
x
x
x
I
∫
()
∫∫∫
=
+
−
+
+
+
+=
2
2
22
1
11
2
ln
x
dx
x
dx
dx
x
x
x
(
)
(
)
=
+
−+
+
+
+=
∫∫
2
2
2
2
1
arctg
1
1
ln
x
dx
x
x
xd
x
=
()
(
)
+
+
−+++
2
2
12
arctg1lnln
x
x
xxx
=+ Cxarctg
2
1
=
()
(
)
C
x
x
xxx +
+
−+++
2
2
12
arctg
2
3
1lnln .
Для интеграла
()
∫
+
2
2
1x
dx
мы использовали решение примера 5 § 1.3.
Упражнения
Найти интегралы от рациональных функций:
1.4.1.1.
∫
−
dx
x
x
1
3
. 1.4.1.2.
∫
+
dx
x
x
1
2
5
.
1.4.1.3.
∫
+
dx
x
x
1
4
9
.
1.4.1.4.
∫
−−
−
dx
xx
x
43
105
2
.
1.4.1.5.
∫
−+
−
dx
xx
x
245
14
2
.
1.4.1.6.
∫
−
+−
dx
xx
xx
4
41211
3
2
.

1.4.1.7. dx
xx
xxx
∫
+−
+++
45
425
24
23
.
1.4.1.8.
∫
−
23
xx
dx
.
1.4.1.9.
∫
+−
−−
dx
xxx
xx
44
43
23
2
.
1.4.1.10.
()
∫
−
2
3
1xx
dx
.
1.4.1.11.
∫
++
+
dx
xx
x
22
74
2
.
1.4.1.12.
∫
+++
++
dx
xxx
xx
44
467
23
2
.
1.4.1.13.
∫
+
+++
dx
xx
xxx
24
235
4
1242
.
1.4.1.14.
∫
++++
dx
xxxx 1222
4
234
.
1.4.1.15.
∫
++
++−
dx
xx
xxx
45
22210
24
23
. 1.4.1.16.
∫
−
−−−
dx
x
xxx
4
193103
23
.
1.4.1.17.
()
∫
+
+
dx
x
x
2
2
1
12
.
1.4.1.18.
∫
++++
−++
dx
xxxx
xxx
2024164
6652
234
23
.
1.4.1.19.
∫
+
++++
dx
x
xxxx
1
42623
2
234
.
1.4.1.20.
∫
−−
−
dx
xx
x
103
134
2
.
1.4.1.21.
∫
++
+
dx
xx
x
106
82
2
.
1.4.1.22.
∫
−
−−−
dx
x
xxx
5
194653
23
.
1.4.1.23.
∫
+
++++
dx
x
xxxx
16
49965163
2
234
.
1.4.1.24.
∫
−+
+
dx
xx
x
20
165
2
. 1.4.1.25.
∫
++
+
dx
xx
x
2610
428
2
.
2°. Интегрирование тригонометрических выражений
Рассмотрим интеграл , где m, n − целые числа.
∫
⋅ xdxx
mn
cossin
Пусть n (или m) − натуральное нечетное число, n = 2k + 1, тогда
∫∫
=⋅⋅=⋅
+
xdxxxdxxx
mkmk
sincossincossin
212
=
()
()
∫
−− xxdx
m
k
coscoscos1
2
сводится к интегралу от степенной функции после замены переменной
t = cosx.
Если же
m и n натуральные и четные, то применяют формулы понижения степени:
2
2cos1
cos;
2
2cos1
sin
22
x
x
x
x
+
=
−
=
.
Примеры
1.
=⋅⋅=⋅
∫∫
xdxxxdxxx coscossincossin
4252
()
()
=−⋅=
∫
xdxx sinsin1sin
2
22
I.
Сделав замену переменной t = sinx, получим
I
() ( )
=++−=+−=−=
∫∫
C
ttt
dttttdttt
75
2
3
21
753
642
2
22
C
xxx
++−=
7
sin
5
sin2
3
sin
753
.
2.
∫
x
dx
6
cos
=
()
()
=+==
∫∫ ∫
xdx
x
dx
xx
dx
tgtg1
coscos
1
cos
2
2
246
I.
Выполнив замену переменной
t = tgx, получаем
I =
()
(
)
∫∫
=++=+ dtttdtt
42
2
2
211 =+++ C
tt
t
53
2
53
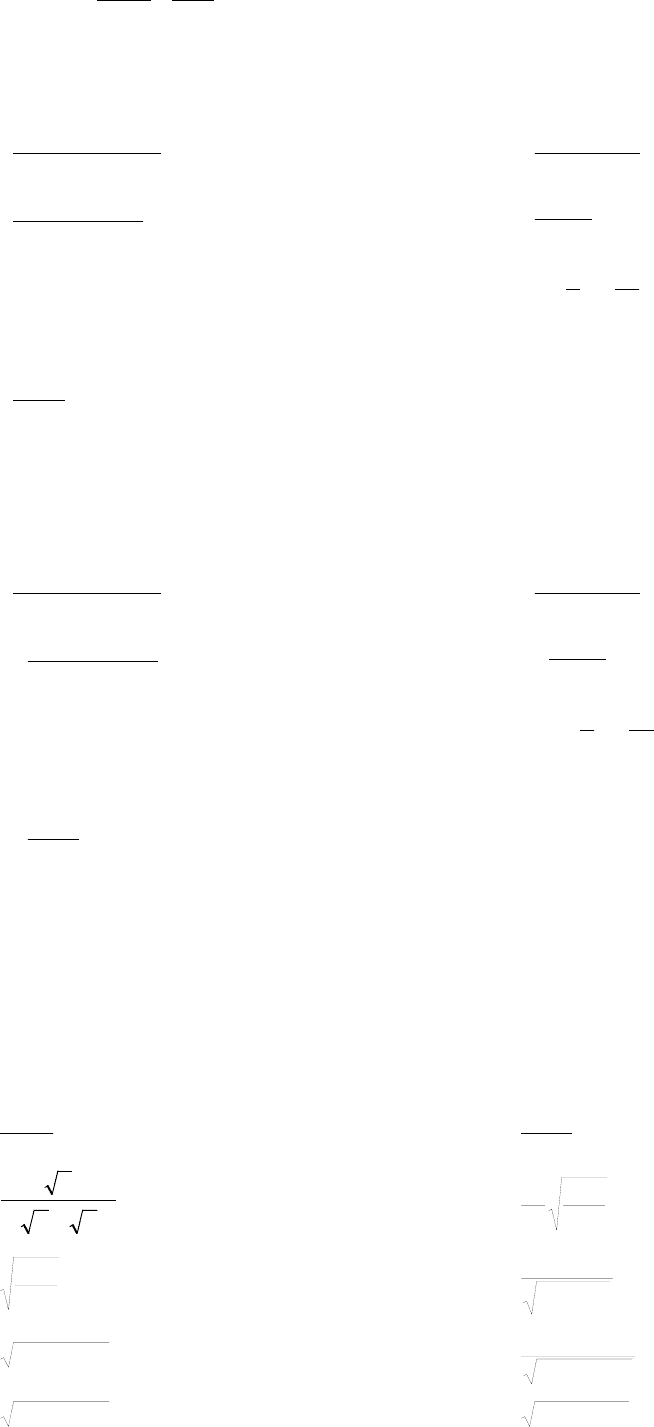
=
C
xx
x +++
5
tg
3
tg2
tg
53
.
Упражнения
Найти интегралы от тригонометрических выражений:
1.4.2.1.
∫
++ 3sin2cos xx
dx
. 1.4.2.2.
∫
+
+
dx
x
xx
2sin3
cossin
.
1.4.2.3.
∫
−
dx
xx cos4sin3
5
.
1.4.2.4.
∫
−
−
dx
x
x
tg1
tg1
.
1.4.2.5. .
∫
xdxx 3cos5sin
1.4.2.6.
∫
dx
xx
2
5
cos
2
cos .
1.4.2.7. .
∫
xdxx
23
cossin 1.4.2.8. .
∫
xdx
4
sin
1.4.2.9.
∫
x
dx
4
sin
.
1.4.2.10. .
∫
xdxx
34
cossin
1.4.2.11. .
∫
xdxx 3cos2sin 1.4.2.12. .
∫
xdxx 5sin6sin
1.4.2.13. .
∫
xdxx 8cos4cos
1.4.2.14. .
∫
−
xdxx
14
cossin
1.4.2.15. .
∫
xdxx 3cos4sin 1.4.2.16. .
∫
xdxx 6cos9cos
1.4.2.17.
∫
++ 3sin2cos xx
dx
. 1.4.2.18.
∫
+
+
dx
x
xx
2sin3
cossin
.
1.4.2.19.
∫
−
dx
xx cos4sin3
5
.
1.4.2.20.
∫
−
−
dx
x
x
tg1
tg1
.
1.4.2.21. .
∫
xdxx 3cos5sin
1.4.2.22.
∫
dx
xx
2
5
cos
2
cos .
1.4.2.23. .
∫
xdxx
23
cossin 1.4.2.24. .
∫
xdx
4
sin
1.4.2.25.
∫
x
dx
4
sin
.
1.4.2.26. .
∫
xdxx
34
cossin
1.4.2.27. .
∫
xdxx 3cos2sin 1.4.2.28. .
∫
xdxx 5sin6sin
1.4.2.29. .
∫
xdxx 8cos4cos
1.4.2.30. .
∫
−
xdxx
14
cossin
1.4.2.31. .
∫
xdxx 3cos4sin 1.4.2.32. .
∫
xdxx 6cos9cos
§ 1.5. Задачи на разные методы интегрирования
1.5.1.
∫
+
dx
e
e
x
x
2
3
. 1.5.2.
∫
−
dx
x
x
12
2
2
.
1.5.3.
()
∫
−
dx
xxx
x
3
4
.
1.5.4.
∫
+
−
dx
x
x
x
1
11
2
.
1.5.5.
∫
+
−
dx
x
x
1
1
.
1.5.6.
()
∫
+
3
2
9 x
dx
.
1.5.7.
∫
−+ dxxx
2
23.
1.5.8.
∫
++
dx
xx
x
84
2
.
1.5.9.
∫
++ dxxx 54
2
. 1.5.10.
∫
++ dxxx 38
2
.

1.5.11. .
∫
+
dxe
xe
x
1.5.12. .
∫
+
dxe
xx ln
1.5.13.
∫
−+ 2
2 xx
ee
dx
. 1.5.14.
∫
dx
x
x
2
arctg
.
1.5.15.
(
)
∫
+
+
dx
xx
x
1
23
22
2
.
1.5.16.
∫
dx
x
x
2
sin
cosln
.
1.5.17.
∫
+ 4
4
x
dx
.
1.5.18.
∫
−
dx
x
x
1
4
6
.
1.5.19. .
∫
xdx
9
tg 1.5.20. .
∫
xdx
7
ctg
1.5.21. .
∫
+ dxx )4ln(
2
1.5.22. Найти функцию q = q(p), q(1) = 1, если дана ее эластичность E
q
= 2p − 3.
1.5.23. Найти функцию q = q(p), q(0) = 1, если дана ее эластичность E
q
= 2p
2
.
1.5.24. Найти функцию q = q(p),
()
e
q
1
0
= , если дана ее эластичность E
q
= p
2
e
−p
.
1.5.25. Пусть темп роста актива от времени задан функцией
r(t) = 2lnt. Найти функцию стоимости актива K = K(t), если K(1) = e
−2
.
Глава 2
Определенный интеграл
§ 2.1. Определение и свойства
1°. К понятию определенного интеграла приводят разнообразные задачи вычисления площадей,
объемов, работы, объема производства, денежных потоков и т.п. В этих задачах приходится встречаться с
отысканием сумм специального вида.
2
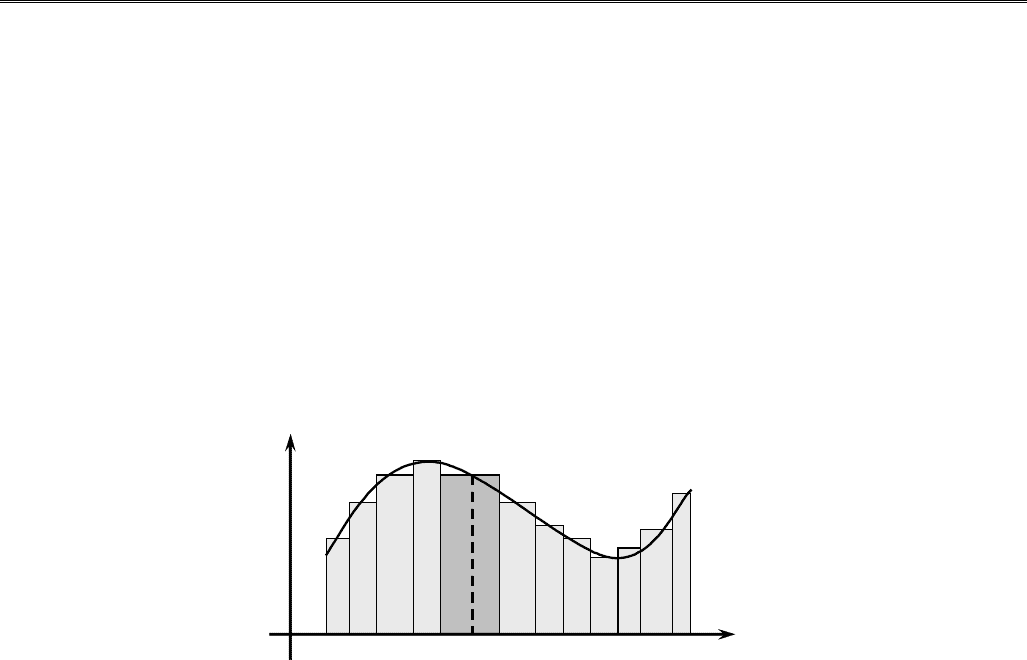
°. Пусть на отрезке [a, b] задана ограниченная функция
y = f(x). Рассмотрим разбиение T отрезка [a, b] точками a = x
0
< x
1
< x
2
< ... < x
n−1
< x
n
= b. Для каждого
отрезка разбиения [
x
k
, x
k+1
] определим его длину
kkk
xxx
−
=
∆
+1
, выберем в нем произвольную точку ,
найдем значение функции
y = f(x) в ней M
k
m
k
=f( ) и составим для разбиения T интегральную сумму S
k
m
T
=
. На рис. 2.1 этой сумме соответствует площадь ступенчатой фигуры.
∑
−
=
∆
1
0
n
k
kk
xM
2
x
1n
x
−2n
x
−
k
M
A
O
B
x
k
1k
x
+
A
a
b
1
x
y
x
k
m
Рис. 2.1.
Число характеризует "степень мелкости" разбиения T; чем меньше это число, тем
мельче разбиение T. Если разбиения T выбираются так, что при n , то будем говорить
о
неограниченном измельчении разбиения отрезка
k
k
xTd ∆= max)(
...,,
21
T 0)( →
n
Td ∞→
[
]
ba,.
3
°. Определение. Если при 0, т.е. при любом неограниченном измельчении разбиения отрезка
, интегральная сумма S
)( →Td
[
ba,
]
T
стремится к определенному пределу, то этот предел называют
определенным интегралом функции
(
)
xfy = на отрезке
[
]
ba, и обозначают . В этом случае
функцию f
(x) называют интегрируемой на отрезке
()
∫
b
a
dxxf
[
]
ba, .
Достаточным условием интегрируемости функции на отрезке является ее непрерывность.
4
°. Формула Ньютона–Лейбница для нахождения определенного интеграла для функции f(x),
интегрируемой на отрезке
[]
ba,:
() () ()
aFbFdxxf
b
a
−=
∫
,
где
F(x) − любая первообразная для функции f(x) на
[
]
ba,.
5
°. Основные свойства.
1)
.
() ()
[]
() ()
∫∫∫
+=+
b
a
b
a
b
a
dxxgdxxfdxxgxf
2)
, A = const.
() ()
∫∫
=
b
a
b
a
dxxfAdxxAf
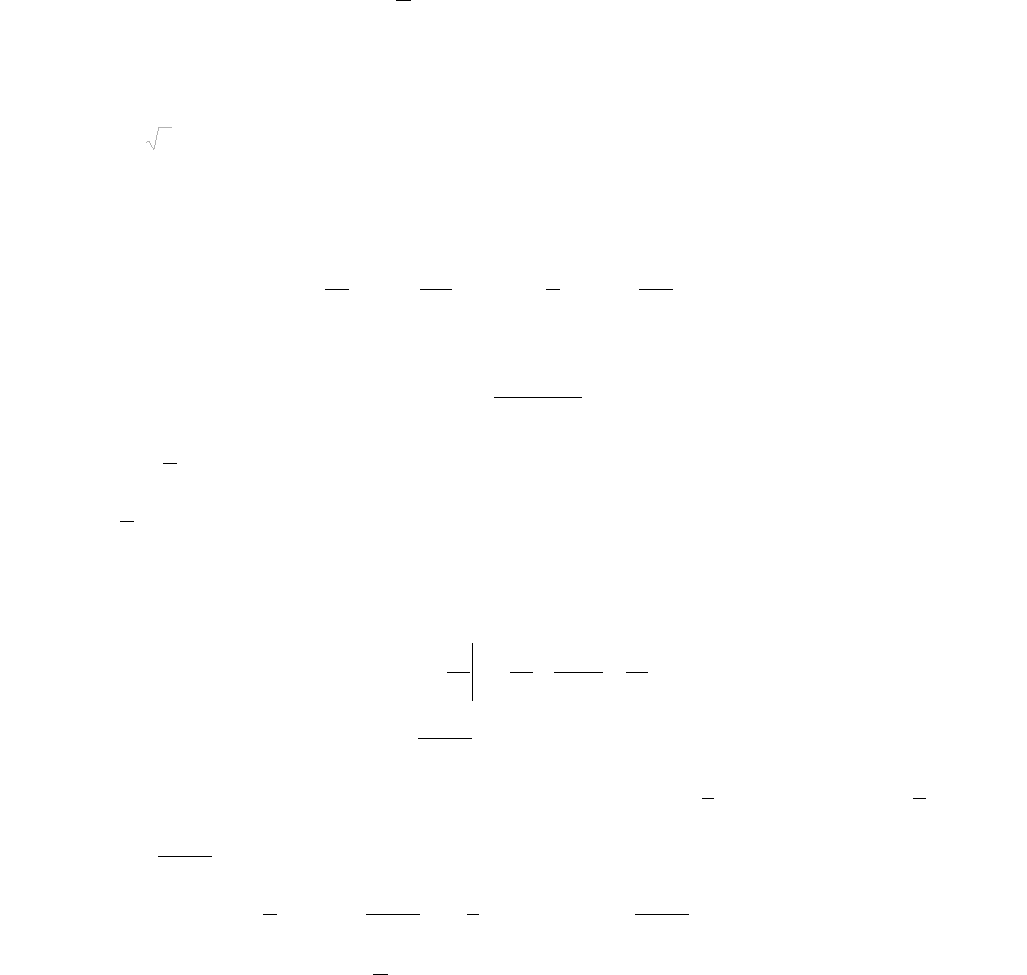
3)
; .
()
0=
∫
a
a
dxxf
() ()
∫∫
−=
a
b
b
a
dxxfdxxf
4)
для любых a, b, c.
() () ()
∫∫∫
+=
b
c
c
a
b
a
dxxfdxxfdxxf
5)
Если f(x) ≤ g(x) на отрезке
[
, то .
]
ba,
() ()
∫∫
≤
b
a
b
a
dxxgdxxf
6)
Если на отрезке
[
]
ba,
)
выполняются неравенства
m ≤ f(x) ≤ M, то (оценка интеграла).
()() (
abMdxxfabm
b
a
−≤≤−
∫
7) Теорема о среднем. Для непрерывной на отрезке [a, b]
функции найдется точка c∈
()
xfy =
[
]
ba, , что
() ()( )
abcfdxxf
b
a
−=
∫
.
Примеры
1.
Найти определенный интеграл
∫
2
1
1
dx
x
с помощью интегральных сумм.
Решение.
Разобьем отрезок [1; 2] на п частей так, чтобы точки деления x
i
(i = 0, 1, 2, ..., п)
составляли геометрическую прогрессию:
x
0
= 1; x
1
= q; x
2
= q
2
; x
3
= q
3
; . . . ,
x
n
= q
n
= 2,
откуда
n
q 2=
)1(
1
−
−
q
n
=
i
.
Длина i-го частичного отрезка равна , так что
при , т.е. при q → 1. В качестве точек m
)1(
1
−=−=∆
+
qqqqx
iii
i
0max →=∆ qx
i
1
+
=
i
qx
∞→n
i
выберем правые концы частичных
отрезков, т.е. m.
1+i
Составим интегральную сумму:
).12(
2
1
)1()1(
11
/1
/1
1
0
1
1
0
−=−=−=∆=
∑∑
−
=
+
−
=
n
n
i
n
i
i
i
n
i
i
T
nq
q
n
qq
q
x
m
S
Остается найти предел интегральной суммы:
,2ln
2
)12(
limlim
/1
/1
=
−
=
∞→∞→
n
n
n
T
n
n
S
так как ~ 12
/1
−
n
2ln
1
n
при . ∞→n
Итак, 2ln
1
2
1
=
∫
dx
x
.
2. Найти определенный интеграл , используя формулу Ньютона–Лейбница.
∫
−
2
1
3
dxx
Решение. Поскольку функция
x
3
непрерывна, то она интегрируема.
()
4
15
4
1
4
2
4
4
4
2
1
4
2
1
3
=
−
−==
−
−
∫
x
dxx
.
3. Оценить определенный интеграл
∫
−
−
2
0
2
9
5
dx
x
x
.
Решение. С помощью производной находим наибольшее
5
3
=
M и наименьшее
2
1
=
m значения
функции
()
2
9
5
x
x
xf
−
−
= на отрезке [0; 2]. Тогда
() (
02
5
3
9
5
02
2
1
2
0
2
−≤
−
−
≤−
∫
dx
x
x
)
, или 2,1
9
5
2
0
2
≤
−
−
≤
∫
dx
x
x
1 .
Точное значение интеграла равно
0472,13ln5ln
3
4
≈− .

Упражнения
2.1.1.
Дайте определение функции ), интегрируемой на отрезке [ . (xf ],ba
2.1.2. Приведите пример функции, которая имеет точку разрыва на отрезке ], но является
интегрируемой на этом отрезке.
,[ ba
2.1.3. Приведите пример функции, которая ограничена на отрезке ][ , но не является интегрируемой на
этом отрезке.
,ba
С помощью интегральных сумм найти интегралы:
2.1.4. .
∫
1
0
2xdx 2.1.5. .
∫
1
0
2
3 dxx
2.1.6.
∫
2
1
2
x
dx
.
2.1.7. .
∫
e
xdx
1
ln 2.1.8. .
∫
π
0
sin xdx
Оценить интегралы:
2.1.9.
∫
−
+
1
1
3
27 x
dx
. 2.1.10.
∫
+
π
2
0
cos28 x
dx
. 2.1.11.
∫
+
2
4
2
sin4
π
π
dxx
.
2.1.12.
∫
−
1
0
2
9 dxx .
2.1.13.
∫
2
4
sin
π
π
dx
x
x
.
2.1.14. .
∫
−
1
0
2
2
dxex
x
2.1.15. .
∫
π
2
0
2
sin xdx 2.1.16. .
∫
2
0
2
dxe
x
2.1.17.
∫
3.
0
tg
π
xdx .
Найти определенные интегралы с помощью формулы Ньютона–Лейбница:
2.1.18.
.
∫
4
0
3
dxx
2.1.19.
∫
2
1
e
x
dx
.
2.1.20. .
∫
π
π
2
sin xdx
2.1.21. .
∫
π
0
2sin xdx
2.1.22.
∫
+
2
1
2
2
1
dx
x
x
.
2.1.23.
∫
5
0
5
dxe
x
.
2.1.24.
∫
+
8
3
1 x
dx
.
2.1.25.
∫
−
2
1
12x
dx
.
2.1.26.
∫
2
1
3
x
dx
.
2.1.27.
∫
−
1
0
2
4 x
dx
.
2.1.28.
∫
+
1
0
2
1x
dx
.
2.1.29.
∫
+
4
1
2
1
dx
x
x
.
2.1.30.
∫
−
−
++
1
2
2
54xx
dx
.
2.1.31.
∫
−+
1
0
2
23 xx
dx
.
2.1.32. .
∫
π
0
2
cos xdx
2.1.33.
∫
+
e
dx
x
x
1
ln1
.
2.1.34.
∫
+
3
0
3
1
dx
x
x
.
2.1.35.
∫
−+
1
0
2
1)78( dxxx .
2.1.36.
∫
−−
2
0
2
24sin5sin
cos
11
π
dx
xx
x
.
2.1.37.
∫
+
3
1
2
1
dx
x
x
.
2.1.38. Найти производную функции dt
t
t
xg
x
∫
=
2
0
sin
)(.
2.1.39. Приведите формулу Ньютона–Лейбница.
2.1.40. Докажите, что .
() ()
[]
() ()
∫∫∫
+=+
b
a
b
a
b
a
dxxgdxxfdxxgxf
2.1.41. Докажите, что для произвольных постоянных α, β.
() ()( ) () ()
∫∫∫
+=+
b
a
b
a
b
a
dxxgdxxfdxxgxf
βαβα
2.1.42. В чем заключается геометрический смысл определенного интеграла от функции на отрезке
? Приведите пример.
()
xf
],[ ba
2.1.43. Дайте определение интеграла с переменным верхним пределом. Чему равна его производная по
верхнему пределу? Ответ обоснуйте.
2.1.44. Выведите формулу Ньютона–Лейбница для определенного интеграла.
2.1.45. Докажите, что интеграл с переменным верхним пределом dttf
x
a
∫
)(
x
, где , является
первообразной функции
, непрерывной на отрезке [ .
bxa ≤≤
()
xf ],ba
§ 2.2. Методы интегрирования
1
°. Замена переменной в определенном интеграле
Пусть в определенном интеграле с непрерывной подынтегральной функцией f(x) производят
замену переменной
x =
ϕ
(t), причем функция
ϕ
(t) непрерывно дифференцируема на отрезке [
α
,
β
] и
()
∫
b
a
dxxf
ϕ
(
α
) = a,
ϕ
(
β
) = b,
ϕ
([
α
,
β
]) = [a, b].
Тогда справедливо равенство
() ()
[]
()
∫∫
′
=
β
α
ϕϕ
dtttfdxxf
b
a
.
Примеры
1.
Найти
∫
+
1
0
21
dx
x
x
.
Решение. Выполним замену переменной xt 21+= . Выражая x через t, получим
(
)
4
1
2
−
=
t
x =
ϕ
(t). Очевидно, что функция
ϕ
(t) непрерывно дифференцируема,
α
= 1 + 2⋅ = 1,
β
= 1 + 2⋅1 = 3,
ϕ
([1; 3]) =
[0; 1], так что все условия выполнены. Поэтому
()
=
+−=
−
=
−
−
=
+
∫∫∫∫
3
1
3
1
2
3
1
1
0
1
2
4
11
4
1
2
1
2
1
21
dt
t
tdt
t
t
dt
t
t
t
dx
x
x
275,0
4
3ln
ln2
24
1
3
1
2
≈=
+−= tt
t
.
2. Найти
∫
−
5
0
2
25 dxx .
Решение. Положим x = 5sint. Легко проверить, что все условия замены переменной выполняются,
новые пределы интегрирования записываем в таблицу:
x
0 5
t
0
π/2
Тогда имеем
=
+
==⋅=−
∫∫∫∫
2
0
2
0
2
2
0
5
0
2
2
2cos1
25cos25cos5cos525
πππ
dt
t
tdttdttdxx
()
4
25
0sinsin
4
25
0
22
25
2sin
4
25
2
25
2
0
π
π
π
π
=−+
−=+= tt .
