Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics
Подождите немного. Документ загружается.


304 17 Datum transformation problems
linearization, approximate starting values and iterations. In this chapter, we solve
the problem algebraically using;
(a) Procrustes,
(b) Groebner basis,
(c) Gauss-Jacobi c ombinatorial algorithms, and
(d) Dixon’s resultant.
Before we present the usage of these algebraic algorithms, let us see how the 7-
parameter datum transformation problem is formulated.
Formulation of the problem
Consider a case where coordinates have been given in two systems, A and B. For
clarity purposes, let us assume the two coordinate systems to be e.g., photo image
coordinates in system A and ground coordinates in system B (see e.g., Fig. 14.7 on
p. 261). The ground coordinates {X
i
, Y
i
, Z
i
|i, . . . , n} of the objects are obtained
from, say, GPS measurements. Given the photo coordinates {a
i
= x
i
, b
i
= y
i
, c
i
=
−f|i, . . . , n} and their equivalent ground coordinates {X
i
, Y
i
, Z
i
|i, . . . , n}, the 7-
parameter datum transformation problem concerns itself with determining;
(1) the s cale parameter x
1
∈ R,
(2) three translation parameters x
2
∈ R
3
, and
(3) the rotation matrix X
3
∈ R
3×3
comprising three rotation elements.
Once the listed unknowns have been determined, coordinates can subsequently be
transformed from one system onto another. The nonlinear equations relating these
unknowns and co ordinates from both systems are given by (cf., equation 14.29 on
p. 262)
a
i
b
i
c
i
= x
1
X
3
X
i
Y
i
Z
i
+ x
2
| i = 1, 2, 3, . . ., n, (17.1)
subject to
X
0
3
X
3
= I
3
. (17.2)
In (17.1), {a
i
, b
i
, c
i
} and {X
i
, Y
i
, Z
i
} are the coordinates of the same points, e.g.,
in both photo and ground coordinate systems respectively. The determination of
the unknowns x
1
∈ R, x
2
∈ R
3
, X
3
∈ R
3×3
require a minimum of three points in
both systems whose coordinates are known. Owing to the nonlinearity of (17.1),
the solutions have always been obtained using a least squares approach iteratively.
With this approach, (17.1) is first linearized and some initial approximate starting
values of the unknown parameters used. The procedure then iterates, each time
improving on the solutions of the preceding iteration step. This is done until a
convergence criteria is achieved.
17-2 Algebraic solution of the 7-parameter transformation problem 305
Where the rotation angles are small e.g., in photogrammetry, the starting values
of zeros are normally used. In other fields such as geodesy, the rotation angles
are unfortunately not small enough to be initialized by zeros, thereby making the
solution process somewhat difficult and cumbersome. Bad choices of initial starting
values often lead to many iterations being required before the convergence criteria
is achieved. In some cases, where the initial starting values are far from those
of the unknown parameters, iteration processes may fail to converge. With these
uncertainties in the initial starting values, the cumbersomeness of the linearization
and iterations, procedures that would offer an exact solution to the 7-parameter
datum transformation problem would be desirable. To answer this challenge, we
prop os e algebraic approaches whose advantages over the approximate numerical
methods have already been mentioned.
Apart from the computational difficulties associated with nume rical proce-
dures, the 7-parameter datum transformation problem poses another challenge to
existing algorithms. This is , the incorporation of the variance-covariance (weight)
matrices of the two systems involved. Communications b etween [245, 266, 344]
on the subject, following the work of [265], provides an insight to this problem.
In practice, users have been forced to rely on iterative procedures and linearized
least squares solutions which are incapable of incorporating the variance-covariance
matrices of both systems in play. We will attempt to address this challenge alge-
braically in this chapter.
17-2 Algebraic solution of the 7-parameter transformation
problem
17-21 Groebner basis transformation
By making use of the skew-symmetric matrix S, the rotation matrix X
3
∈ R
3×3
in (17.1) is expressed as
X
3
= (I
3
− S)
−1
(I
3
+ S), (17.3)
where I
3
is the identity matrix and the skew-symmetric matrix S given by
S =
0 −c b
c 0 −a
−b a 0
. (17.4)
The rotation matrix X
3
∈ R
3×3
is parameterized using Euler or Cardan angles.
With Cardan angles, we have:
Solution 17.1 (Parametrization of the rotation matrix by Cardan an-
gles).
X
3
= R
1
(α)R
2
(β)R
3
(γ) (17.5)
with

306 17 Datum transformation problems
R
1
=
1 0 0
0 cosα sinα
0 −sinα cosα
, R
2
=
cosβ 0 −sinβ
0 1 0
sinβ 0 cosβ
, R
3
=
cosγ sinγ 0
−sinγ cosγ 0
0 0 1
,
leading to
R
1
(α)R
2
(β)R
3
(γ) =
cosβcosγ cosβsinγ −sinβ
sinαsinβcosγ − cosαsinγ sinαsinβsinγ + cosαcosγ sinαcosβ
cosαsinβcosγ + sinαsinγ cosαsinβsinγ − sinαcosγ cosαcosβ
.
(17.6)
The Cardan angles are then obtained from the rotation matrix X
3
∈ R
3×3
through:
α = tan
r
23
r
33
γ = tan
r
12
r
11
β = tan
(
−r
31
p
r
2
11
+ r
2
12
)
= tan
(
−r
31
p
r
2
23
+ r
2
33
)
.
(17.7)
For parametrization using Euler angles, we have:
Solution 17.2 (Parametrization of the rotation matrix by Euler angles
Λ
Γ
, Φ
Γ
, Σ
Γ
).
R
E
(Λ
Γ
, Φ
Γ
, Σ
Γ
) := R
3
(Σ
Γ
)R
2
(
π
2
− Φ
Γ
)R
3
(Λ
Γ
) (17.8)
R
1
:=
1 0 0
0 cos 1 sin 1
0 −sin 1 cos 1
, R
2
:=
cos 2 0 −sin 2
0 1 0
sin 2 0 cos 2
, R
3
:=
cos 3 sin 3 0
−sin 3 cos 3 0
0 0 1
(17.9)
R
3
(Λ
Γ
) =
cos Λ
Γ
sin Λ
Γ
0
−sin Λ
Γ
cos Λ
Γ
0
0 0 1
, R
2
(
π
2
− Φ
Γ
) =
sin Φ
Γ
0 −cos Φ
Γ
0 1 0
cos Φ
Γ
0 sin Φ
Γ
(17.10)
R
2
(
π
2
− Φ
Γ
)R
3
(Λ
Γ
) =
sin Φ
Γ
cos Λ
Γ
sin Φ
Γ
sin Λ
Γ
−cos Φ
Γ
−sin Λ
Γ
cos Λ
Γ
0
cos Φ
Γ
cos Λ
Γ
cos Φ
Γ
sin Λ
Γ
sin Φ
Γ
(17.11)

17-2 Algebraic solution of the 7-parameter transformation problem 307
R := R
3
(Σ
Γ
)R
2
(
π
2
− Φ
Γ
)R
3
(Λ
Γ
) =
cos Σ
Γ
sin Φ
Γ
cos Λ
Γ
−sin Σ
Γ
sin Λ
Γ
cos Σ
Γ
sin Φ
Γ
sin Λ
Γ
+ sin Σ
Γ
cos Λ
Γ
−cos Σ
Γ
cos Φ
Γ
−sin Σ
Γ
sin Φ
Γ
cos Λ
Γ
−cos Σ
Γ
sin Λ
Γ
−sin Σ
Γ
sin Φ
Γ
sin Λ
Γ
+ cos Σ
Γ
cos Λ
Γ
sin Σ
Γ
cos Φ
Γ
cos Φ
Γ
cos Λ
Γ
cos Φ
Γ
sin Λ
Γ
sin Φ
Γ
0 ≤ Λ
Γ
< 2π, −
π
2
< Φ
Γ
< +
π
2
, 0 ≤ Σ
Γ
< 2π
(17.12)
The inverse map of
R = [r
kl
] ,k,l ∈ {1, 2, 3},
to
(Λ
Γ
, Φ
Γ
, Σ
Γ
)
is given by Lemma 17.1.
Lemma 17.1 (Inverse map R 7→ Λ
Γ
, Φ
Γ
, Σ
Γ
). Let the direct Euler map of the
rotation matrix be given by (17.12), namely
R := R
3
(Σ
Γ
)R
2
(
π
2
− Φ
Γ
)R
3
(Λ
Γ
),
(Λ
Γ
, Φ
Γ
, Σ
Γ
) ∈
n
R
3
0 ≤ Λ
Γ
< 2π, −
π
2
< Φ
Γ
< +
π
2
, 0 ≤ Σ
Γ
< 2π
o
.
The inverse Euler map is parameterized by
tan Λ
Γ
=
r
32
r
31
⇒ Λ
Γ
= arctan
r
32
r
31
tan Φ
Γ
=
r
33
p
r
2
31
+ r
2
32
⇒ Φ
Γ
= arctan
r
33
p
r
2
31
+ r
2
32
tan Σ
Γ
= −
r
23
r
13
⇒ Σ
Γ
= arctan −
r
23
r
13
.
(17.13)
The properties of the rotation matrix X
3
∈ R
3×3
expressed in (17.3) have been
examined by [434] and shown to fulfill (17.2). Only a minimum of three corre-
sponding points in both systems are required for the transformation parameters
to be obtained. For these points, (17.1) is now written for i = 1, 2, 3 using (17.3)
as
1 c −b
−c 1 a
b −a 1
a
i
b
i
c
i
= x
1
1 −c b
c 1 −a
−b a 1
X
i
Y
i
Z
i
+
1 c −b
−c 1 a
b −a 1
X
0
Y
0
Z
0
, (17.14)
with {X
0
, Y
0
, Z
0
} ∈ x
2
being the translation parameters. For these three cor-
responding points in both systems, the observation equations for solving the 7
transformation parameters are expressed from (17.14) as:
308 17 Datum transformation problems
f
1
:= x
1
X
1
− x
1
cY
1
+ x
1
bZ
1
+ X
0
+ cY
0
− bZ
0
− a
1
− cb
1
+ bc
1
= 0
f
2
:= x
1
cX
1
+ x
1
Y
1
− x
1
aZ
1
− cX
0
+ Y
0
+ aZ
0
+ ca
1
− b
1
− ac
1
= 0
f
3
:= −x
1
bX
1
+ x
1
aY
1
+ x
1
Z
1
+ bX
0
− aY
0
+ Z
0
− ba
1
+ ab
1
− c
1
= 0
f
4
:= x
1
X
2
− x
1
cY
2
+ x
1
bZ
2
+ X
0
+ cY
0
− bZ
0
− a
2
− cb
2
+ bc
2
= 0
f
5
:= x
1
cX
2
+ x
1
Y
2
− x
1
aZ
2
− cX
0
+ Y
0
+ aZ
0
+ ca
2
− b
2
− ac
2
= 0
f
6
:= −x
1
bX
2
+ x
1
aY
2
+ x
1
Z
2
+ bX
0
− aY
0
+ Z
0
− ba
2
+ ab
2
− c
2
= 0
f
7
:= x
1
X
3
− x
1
cY
3
+ x
1
bZ
3
+ X
0
+ cY
0
− bZ
0
− a
3
− cb
3
+ bc
3
= 0
f
8
:= x
1
cX
3
+ x
1
Y
3
− x
1
aZ
3
− cX
0
+ Y
0
+ aZ
0
+ ca
3
− b
3
− ac
3
= 0
f
9
:= −x
1
bX
3
+ x
1
aY
3
+ x
1
Z
3
+ bX
0
− aY
0
+ Z
0
− ba
3
+ ab
3
− c
3
= 0,
(17.15)
where {x
i
, y
i
, z
i
} := {a
i
, b
i
, c
i
} | i ∈ {1, 2, 3} are coordinates of the three points
in one of the systems (e.g., local system) and {X
i
, Y
i
, Z
i
} | i ∈ {1, 2, 3} are the
corresponding coordinates in the other system (e.g., global system). In (17.15),
{f
1
, f
2
, f
3
} are algebraic e xpressions formed from the first point with coordi-
nates in both systems, {f
4
, f
5
, f
6
} from the second point and {f
7
, f
8
, f
9
} from
the third point. From (17.15), considering the unknowns (see Eqn. 17.14) as
x
1
, a, b, c, X
0
, Y
0
, Z
0
, one requires only seven equations for a closed form solution
of the 7-parameter transformation problem.
Let us consider the system of nonlinear equations extracted from (17.15) to be
formed by the 7 polynomials {f
1
, f
2
, f
3
, f
4
, f
5
, f
6
, f
9
}. Our target now is to solve
algebraically this nonlinear system of equations using Groebner basis approach to
provide symbolic solutions. We proceed as follows: First, the translation parame-
ters {X
0
, Y
0
, Z
0
} are eliminated by differencing
f
14
:= f
1
− f
4
= x
1
X
12
− x
1
cY
12
+ x
1
bZ
12
− a
12
− cb
12
+ bc
12
f
25
:= f
2
− f
5
= x
1
cX
12
+ x
1
Y
12
− x
1
aZ
12
+ ca
12
− b
12
− ac
12
f
39
:= f
3
− f
9
= −x
1
bX
13
+ x
1
aY
13
+ x
1
Z
13
− ba
13
+ ab
13
− c
13
f
69
:= f
6
− f
9
= −x
1
bX
23
+ x
1
aY
23
+ x
1
Z
23
− ba
23
+ ab
23
− c
23
,
(17.16)
where
X
ij
= X
i
− X
j
, Y
ij
= Y
i
− Y
j
, Z
ij
= Z
i
− Z
j
a
ij
= a
i
− a
j
, b
ij
= b
i
− b
j
, c
ij
= c
i
− c
j
| i, j ∈ {1, 2, 3}, i 6= j.
The reduced Groebner basis of (17.16) is then obtained using (4.38) on p. 45 by
GroebnerBasis[{f
14
, f
25
, f
37
, f
67
}, {x
1
, a, b, c}, {a, b, c}].
This gives only the elements of the Groebner basis in which the variables {a, b, c}
have been eliminated and only the scale factor x
1
is left. The scale parameter is
then given by the following quartic polynomial:
a
4
x
4
1
+ a
3
x
3
1
+ a
2
x
2
1
+ a
1
x
1
+ a
0
= 0, (17.17)
with the coefficients as in [23, Boxes 2-2] or [37, Appendix A]. Once the admissible
value of scale parameter x
1
∈ R
+
has been chosen from the four roots in (17.17),
17-2 Algebraic solution of the 7-parameter transformation problem 309
the elements of the skew-symmetric matrix S in (17.4) can then be obtained via
the linear functions in [23, Boxes 2-3] or [37, Appendix B]. Substituting the skew-
symmetric matrix S in (17.1) gives the rotation matrix X
3
, from which the Cardan
rotation angles are deduced using (17.7) in Solution 17.1. The translation elements
x
2
can then be computed by substituting the scale parameter x
1
and the rotation
matrix X
3
in (17.1). Three sets of translation parameters are then obtained, from
which their mean is taken.
Example 17.1 (Computation of transformation parameters using Groebner basis
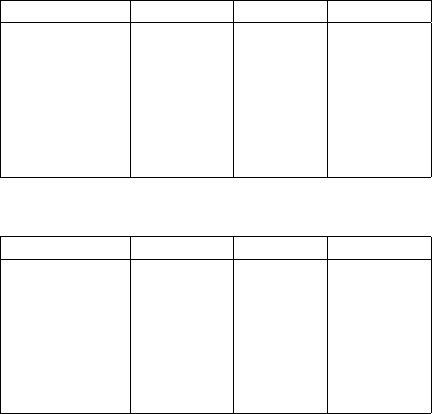
algorithm). Cartesian coordinates of seven stations in Stuttgart Germany are given
in the local and global system (WGS-84) in Tables 17.1 and 17.2 respectively.
Desired are the seven parameters of datum transformation. Using explicit solutions
in [23, Boxes 2-2 and 2-3] or [37, Appendices A and B], the 7 transformation
parameters are computed and presented in Table 17.3. These parameters are then
used to transform the three points involved in the computations from the local
reference system in Table 17.1 to the WGS-84, as shown in Table 17.4.
Table 17.1. Coordinates for system A (local system)
Station Name X(m) Y (m) Z(m)
Solitude 4157222.543 664789.307 4774952.099
Buo ch Zeil 4149043.336 688836.443 4778632.188
Hohenneuffen 4172803.511 690340.078 4758129.701
Kuehlenberg 4177148.376 642997.635 4760764.800
Ex Mergelaec 4137012.190 671808.029 4791128.215
Ex Hof Asperg 4146292.729 666952.887 4783859.856
Ex Kaisersbach 4138759.902 702670.738 4785552.196
Table 17.2. Coordinates for system B (WGS-84)
Station Name X(m) Y (m) Z(m)
Solitude 4157870.237 664818.678 4775416.524
Buo ch Zeil 4149691.049 688865.785 4779096.588
Hohenneuffen 4173451.354 690369.375 4758594.075
Kuehlenberg 4177796.064 643026.700 4761228.899
Ex Mergelaec 4137659.549 671837.337 4791592.531
Ex Hof Asperg 4146940.228 666982.151 4784324.099
Ex Kaisersbach 4139407.506 702700.227 4786016.645
17-22 Dixon resultant solution
In this section we solve the C
7
(3) Helmert transformation with the Dixon resul-
tant using the Kapur-Saxena-Yang (KSY) method (see Kapur et al. [239]), in the
Computer Algebra System of Mathematica. This method was implemented into
Mathematica by Nakos and Williams [309, 308]. In order to evaluate the perfor-
mance of the Dixon resultant, we compared its performance with that of Groebner
basis solution (see the previous section and Z´avoti and Jancso [433]).
As we have seen in the previous section, in order to solve the 7-parameter datum
transformation problem, a minimum of three corresponding p oints in both systems
310 17 Datum transformation problems
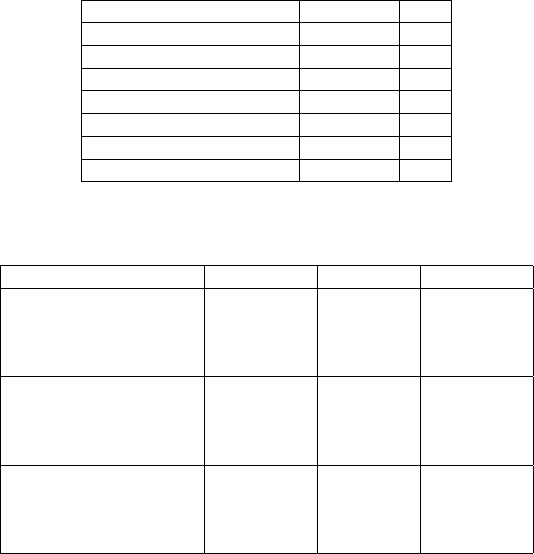
Table 17.3. Groebner basis’ 7-transformation parameters
Transformation parameter Value unit
Scale k − 1 -1.4343 [ppm]
Rotation X
1
(a) 0.32575149 [“]
Rotation X
2
(b) -0.46037399 [“]
Rotation X
3
(c) -0.00810606 [“]
Translation ∆X 643.0953 [m]
Translation ∆Y 22.6163 [m]
Translation ∆Z 481.6023 [m]
Table 17.4. Transformed Cartesian coordinates of System A (Table 17.1) into System
B (Table 17.2) using the parameters in Table 17.3
Site X(m) Y (m) Z(m)
System A: Solitude 4157222.5430 664789.3070 4774952.0990
System B 4157870.2370 664818.6780 4775416.5240
Transformed value 4157870.3070 664818.6742 4775416.5240
Residual - 0.0700 0.0038 0.0000
System A: Buoch Zeil 4149043.3360 688836.4430 4778632.1880
System B 4149691.0490 688865.7850 4779096.5880
Transformed value 4149691.1190 688865.7812 4779096.5880
Residual - 0.0700 0.0038 0.0000
System A: Hohenneuffen 4172803.5110 690340.0780 4758129.7010
System B 4173451.3540 690369.3750 4758594.0750
Transformed value 4173451.2141 690369.3826 4758594.0750
Residual 0.1399 -0.0076 0.0000
are required. For these three points, nine equations (f
1
, f
2
, . . . , f
9
) can be written
(see 17.15). In order to obtain a solvable system of equations, seven equations
should be chosen. In the previous section, a combination was chosen arbitrarily
as {f
1
, f
2
, f
3
, f
4
, f
5
, f
6
, f
9
}. However, there exists
9
7
= 36 possible combinations
of selecting seven equations from the nine original equations in (17.15). From
the selected 7 equations, the translation parameters X
0
, Y
0
, Z
0
are eliminated
in a differential mode (see 17.16) reducing the seven equations to a system of
four equations with four unknown paramete rs (i.e., scale x
1
and rotation elements
a, b, c). After selecting a combination, the possible configurations to eliminate the
translation parameters are:
X
0
Y
0
Z
0
f
1
− f
4
f
2
− f
5
f
3
− f
6
f
1
− f
7
f
2
− f
8
f
3
− f
9
f
4
− f
7
f
5
− f
8
f
6
− f
9
(17.18)
Considering now a different combination than used in the previous section, e.g.,
(f
2
, f
3
, f
4
, f
5
, f
6
, f
8
, f
9
), the eliminations (f
i
− f
j
) whose indices (i, j) cover the
sequence (2, 3, 4, 5, 6, 8, 9) are

17-2 Algebraic solution of the 7-parameter transformation problem 311
r
1
= f
2
− f
8
;
r
2
= f
2
− f
5
;
r
3
= f
3
− f
9
;
r
4
= f
6
− f
9
;
(17.19)
leading to
r
1
= −ca
1
+ ca
3
− cx
1
X
1
+ cx
1
X
3
+ b
1
− b
3
− x
1
Y
1
+ x
1
Y
3
+ ac
1
− ac
3
+ ax
1
Z
1
− ax
1
Z
3
;
r
2
= −ca
1
+ ca
2
− cx
1
X
1
+ cx
1
X
2
+ b
1
− b
2
− x
1
Y
1
+ x
1
Y
2
+ ac
1
− ac
2
+ ax
1
Z
1
− ax
1
Z
2
;
r
3
= ba
1
− ba
3
+ bx
1
X
1
− bx
1
X
3
− ab
1
+ ab
3
− ax
1
Y
1
+ ax
1
Y
3
+ c
1
− c
3
− x
1
Z
1
+ x
1
Z
3
;
r
4
= ba
2
− ba
3
+ bx
1
X
2
− bx
1
X
3
− ab
2
+ ab
3
− ax
1
Y
2
+ ax
1
Y
3
+ c
2
− c
3
− x
1
Z
2
+ x
1
Z
3
;
(17.20)
This system can be simplified using the same new variables as in the previous
section, instead of the original coordinate differences. The simplified system, with
these new variables which we call relative coordinates is
r
1
= −ca
13
− cx
1
X
13
+ b
13
− x
1
Y
13
+ ac
13
+ ax
1
Z
13
;
r
2
= −ca
12
− cx
1
X
12
+ b
12
− x
1
Y
12
+ ac
12
+ ax
1
Z
12
;
r
3
= ba
13
+ bx
1
X
13
− ab
13
− ax
1
Y
13
+ c
13
− x
1
Z
13
;
r
4
= ba
23
+ bx
1
X
23
− ab
23
− ax
1
Y
23
+ c
23
− x
1
Z
23
;
(17.21)
Equation (17.21) can now be solved by eliminating the variables a, b and c to obtain
a polynomial for the scale parameter (x
1
) via the Dixon resultant or Groebner basis
in Mathematica
1
.
First, the Dixon prompt should be called by typing,
<< Resultant ‘Dixon‘
then we can compute the Dixon resultant by
DixonResultant[{r
1
, r
2
, r
3
, r
4
}, {a, b, c}, {σ
1
, σ
2
, σ
3
}]
where {σ
1
, σ
2
, σ
3
} are the auxiliary variables of the Dixon polynomial, r
i
{i =
1, . . . , 4} the equations, and {a, b, c} the variables to be eliminated from the equa-
tion system. This results in a quartic polynomial for the scale factor (x
1
), similar
to the Groebner basis solution (see 17.17). The Dixon resultant takes 0.016 sec-
onds to solve this system of equations on a HP xw 4100 workstation with Windows
XP operation system, 3GHz P4 Intel pro ce ss or and 1 GB RAM. Let us compare
the results now with those of the Gro e bner basis solution. The same result can be
achieved by typing in Mathematica,
GroebnerBasis[{r
1
, r
2
, r
3
, r
4
}, {x
1
, a, b, c}, {a, b, c}]
where r
i
{i = 1, . . . , 4} are the equations, {x
1
, a, b, c} the variables in the system,
and {a, b, c} the variables to be eliminated from the equation system, where the
1
Remark: With the Dixon resultant the system of Eq. (17.20), without using the
relative co ordinates, also provided a solution, which was un-achievable with Groebner
basis (see Pal´ancz et al. [319]).
312 17 Datum transformation problems
order means the elimination order of the variables. However, using the Groebner
basis method requires 3017.69 seconds!
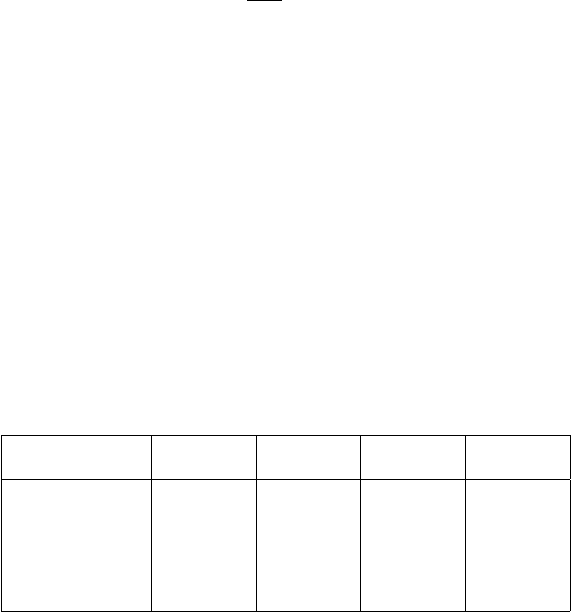
We have chosen different 7-equation combinations from the original 9 equa-
tions and we changed also the monomial order during the processing (see Table
17.5 for a few chosen sequences). The Dixon resultant solution was indifferent to
these changes, the running time always being ca. 0.016 seconds. However, the run-
ning time for the reduced Groebner basis solution was dependent on the chosen
7-equation combination and changes also with the order of variables to be elim-
inated (see Table 17.5). In case of four chosen sequences (from the 36 possible
choices), one notices considerable change in the required computational time, see
for example the last column in Table 17.5. For example, for the combination of
(f
2
, f
3
, f
4
, f
5
, f
6
, f
8
, f
9
), the computation time was 50 minutes using the monomial
order {a, b, c} and only 0.484 seconds if we changed the monomial order to {b, c, a}!
With Dixon resultant, the running time was only 0.016 seconds, independent from
the order of variables. The Groebner basis approach is clearly affected by both
(a) the c ombinatorial sequence and
(b) the monomial order.
These two factors are undesirable since users are not often privy to the optimal
sequence and order during data processing. However, there is a third important
factor having strong influence on the performance of the Groebner basis com-
putation: this is the elimination order. In general, using MonomialOrder − >
EliminationOrder can ensure the b e st behavior, (Lichtblau, Priv. Comm.).
Table 17.5. Running times (seconds ) for cases of different sequences and order of the
variables to be eliminated using reduced Groebner basis with relative coordinates
Sequence f
1
, f
2
, f
3
, f
4
, f
1
, f
2
, f
3
, f
4
, f
1
, f
2
, f
3
, f
4
, f
2
, f
3
, f
4
, f
5
,
Order of variables f
6
, f
7
, f
8
f
5
, f
8
, f
9
f
5
, f
7
, f
9
f
6
, f
8
, f
9
a,b,c 0.219 0.688 0.985 3017.69
a,c,b 0.36 35.921 0.672 2601.75
b,a,c 0.25 0.922 0.765 3172.48
b,c,a 163.765 0.547 33.985 0.484
c,a,b 0.719 52.328 0.562 1831.42
c,b,a 174.547 0.75 47.797 0.532
The Dixon resultant therefore proved to be faster in this case , and very robust
in that it is insensitive to the order of variables, unlike the Groebner basis. This
feature can be very important from a practical point of view, because in the case
of Groebner basis, the user should find the proper combinatorial sequence and
monomial order via a trial-error method. For the sequence (f
2
, f
3
, f
4
, f
5
, f
6
, f
8
, f
9
)
in Table 17.5 for example, only two orders can provide a solution in a reasonable
time from the six possible orders of the variables.
As a test, three Hungarian points in the ETRS89 system (x
1
, y
1
, z
1
, . . . , z
3
)
and in the local Hungarian system HD72 (Hungarian Datum 1972) (X
1
, Y
1
, Z
1
, . . . ,

17-2 Algebraic solution of the 7-parameter transformation problem 313
Z
3
) listed in Table 17.6 were used. Both Dixon and Groebner basis yielded identical
results. These examples are available on Mathematica in notebook format
2
.
Table 17.6. Hungarian points in the ETRS89 and HD72 datums
Point x(m) y(m) z(m) X(m) Y(m) Z(m)
1 4171409.677 1470823.777 4580140.907 4171352.311 1470893.887 4580150.178
2 4146957.889 1277033.850 4659439.264 4146901.301 1277104.509 4659448.287
3 3955632.880 1611863.197 4720991.316 3955575.649 1611933.124 4721000.952
17-23 Gauss-Jacobi combinatorial transformation
When more than three points in both systems are given and the transformation
parameters desired, the Gauss-Jacobi combinatorial algorithm is applied. In such a
case, the dispersion matrix has to be obtained via the nonlinear error propagation
law/variance-covariance propagation law. From the algebraic system of equations
(17.15), the Jacobi matrices are given (using e.g., (7.30) and (7.31) on p. 94) as
J
x
=
∂f
1
∂x
1
∂f
1
∂a
∂f
1
∂b
∂f
1
∂c
∂f
1
∂X
0
∂f
1
∂Y
0
∂f
1
∂Z
0
∂f
2
∂x
1
∂f
2
∂a
∂f
2
∂b
∂f
2
∂c
∂f
2
∂X
0
∂f
2
∂Y
0
∂f
2
∂Z
0
∂f
3
∂x
1
∂f
3
∂a
∂f
3
∂b
∂f
3
∂c
∂f
3
∂X
0
∂f
3
∂Y
0
∂f
3
∂Z
0
∂f
4
∂x
1
∂f
4
∂a
∂f
4
∂b
∂f
4
∂c
∂f
4
∂X
0
∂f
4
∂Y
0
∂f
4
∂Z
0
∂f
5
∂x
1
∂f
5
∂a
∂f
5
∂b
∂f
5
∂c
∂f
5
∂X
0
∂f
5
∂Y
0
∂f
5
∂Z
0
∂f
6
∂x
1
∂f
6
∂a
∂f
6
∂b
∂f
6
∂c
∂f
6
∂X
0
∂f
6
∂Y
0
∂f
6
∂Z
0
∂f
7
∂x
1
∂f
7
∂a
∂f
7
∂b
∂f
7
∂c
∂f
7
∂X
0
∂f
7
∂Y
0
∂f
7
∂Z
0
, (17.22)
and
2
http://library.wolfram.com/infocenter/MathSource/6654/
