Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

272 15 GNSS environmental monitoring

zenith Delay = 10

∞

antenna

N(z)dz, (15.5)

where the integral is in the zenith direction. Substituting (15.4) in (15.5) leads to

the calculation of the zenith wet delay which is related to the total amount of water

vapour along the zenith direction. The zenith delay is considered to be constant

over a certain time interval. It is the average of the individual slant ray path delays

that are projected to the zenith using the mapping functions (e.g., [311]) which

are dependent on the receiver to satellite elevation angle, altitude and time of the

year.

The signiﬁcant application of GPS satellites in ground based GPS meteorology

is the determination of the slant water. If one could condense all the water vapour

along the ray path of a GPS signal (i.e., from the GPS satellite to the ground re-

ceiver), the column of the liquid water after condensation is termed slant water. By

converting the GPS derived tropospheric delay during data processing, slant water

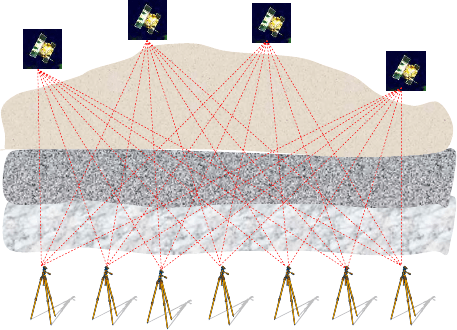
is obtained. By using several receivers to track several satellites (e.g., Fig.15.2

a three-dimensional distribution of water vapour and its time variation can be

quantiﬁed. In Japan, there exist (by 2004) more than 1200 GPS receivers within

the framework of GPS Earth Observing NETwork (GEONET) with a spatial reso-

lution of 12-25km dedicated to GPS meteorology (see e.g., [13, 387]). These dense

network of GPS receivers are capable of delivering information on water vapour

that are useful as already stated in Sect. 15-1.

Figure 15.2. Ground based GPS meteorology

15-3 Refraction (bending) angles 273

15-3 Refraction (bending) angles

In space borne GPS meteorology, the measured quantities are normally the ex-

cess path delay of the signal. It is obtained by measuring the excess phase of the

signal owing to atmospheric refraction during the traveling period. The determi-

nation of the refraction angle α from the measured exce ss phase therefore marks

the beginning of the computational process to retrieve the atmospheric proﬁles

of temperature, pressure, water vapour and geopotential heights. The unknown

refraction angle α is related to the measured excess phase by a system of two

nonlinear trigonometric equations;

1. an equation relating the doppler shift at the Low Earth Orbiting (LEO) satel-

lite (e.g., CHAMP, GRACE etc.) expressed as the diﬀerence in the projected

velocities of the two moving satellites on the ray path tangent on one hand,

and the doppler shift expressed as the sum of the atmosphere free propagation

term and a term due to atmosphere on the other hand,

2. an equation that makes use of Snell’s law in a spherically layered medium [369,

p. 59].

Equations formed from (1) and (2) are nonlinear e.g., (15.6) and have b een solved

using iterative numerical methods such as Newton’s (see e.g., [203, 256, 369, 413].

In-order to solve the trigonometric nonlinear system of equations (15.6), Newton’s

approach assumes the refractive angles to be s mall enough such that the rela-

tionship between the doppler shift and the bending angles formed from (1) and

(2) are linear. The linearity assumption of the relationship between the doppler

shift and refraction angles introduces some small nonlinearity errors. Vorob’ev

and Krasil’nikova [400] have pointed out that neglecting the nonlinearity in (15.6)

causes an error of 2% when the beam perigee is close to the Earth’s ground and

decrease with the altitude of the perigee. The extent of these errors in the dry part

of the atmosphere, i.e., the upper troposphere and lower stratosphere, particularly

the height 5-30 km, whose bending angle data are directly used to compute the at-

mospheric proﬁles or directly assimilated in Numerical Weather Prediction Models

(NWPM) (e.g., [216]) is however not precisely stated. The eﬀects of nonlinearity

error on the impact parameters to which the refraction bending angles are related

is also not known.

In an attempt to circumvent the nonlinearity of (15.6), [400] expand it into

series of V /c, where V is the velocity of the artiﬁcial sate llite and c the veloc ity of

light in vacuum. This c orrects for relativistic eﬀects and introduce the concept of

perturbation. The angle between the relative position vectors of the two satellites

and the tangent velocity vector at GPS is expressed in quadratic terms of the

corresponding angle at LEO (also expanded to the second order). The refraction

angle is then obtained by making use of its inﬁnitesimal values that are less than

−2

. Though the approach attempts to provide an analytic (direct) solution to

nonlinear system of equations for bending angles, it is still nevertheless “quasi-

nonlinear” and as such does not oﬀer a complete, exact solution to the problem.

The fact that there existed no direct (exact) solution to the nonlinear system

274 15 GNSS environmental monitoring

of bending angle’s equations of space borne GPS meteorology had already been

pointed out by [413].

Motivated by Wickert’s [413] observation, we will demonstrate in the next

sections how the algebraic techniques of Sylvester resultant and reduced Groebner

basis oﬀer direct s olution to bending angles’ nonlinear system of equations (15.6).

15-31 Transformation of trigonometric equations to algebraic

The system of nonlinear trigonometric equations for determining the refraction

angles comprises of two equations given as

cos(β

− φ

) − v

cos(φ

+ β

) =

+ v

cos(β

− ψ

) − v

cos(ψ

+ β

)

sinφ

= r

sinφ

(15.6)

where v

, v

are the projected LEO and GPS satellite velocities in the occultation

plane, r

, r

the radius of tangent points at LEO and GPS respectively, and

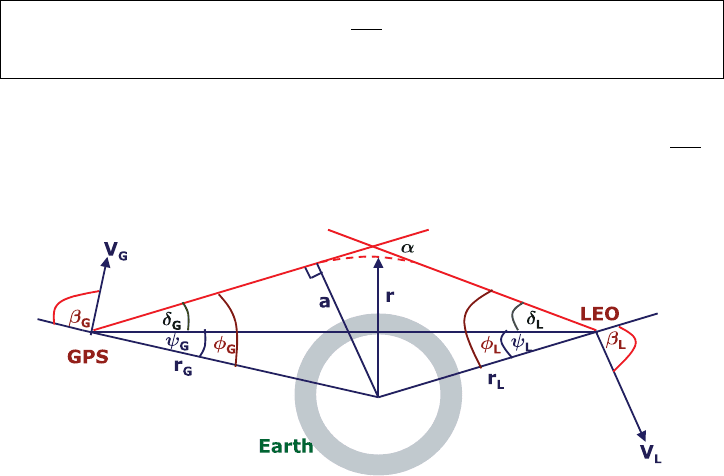
the doppler shift. The angles in (15.6) are as shown in Fig. 15.3.

Figure 15.3. Geometry of space borne GPS meteorology

Let us denote



x = sinφ

, y = sinφ

, a

= v

cosβ

, a

= v

sinβ

= −v

cosβ

, a

= v

sinβ

, a

= r

, a

= −r

(15.7)

where the signs of the velocities change depending on the directions of the satellites.

Using;

• Theorem 3.1 on p. 19,

• the trigonometric addition formulae,

• and (15.7),

15-3 Refraction (bending) angles 275

(15.6) simpliﬁes to



cosφ

+ a

y + a

cosφ

+ a

x = a

x + a

y = 0.

(15.8)

In (15.8), the right-hand-side of the ﬁrst expression of (15.6) has been substituted

with a. In-order to eliminate the trigonometric terms cosφ

and cosφ

appearing

in (15.8), they are taken to the right-hand-side and the resulting expression squared

y + a

x − a)

= (−a

cosφ

− a

cosφ

)

. (15.9)

The squared trigonometric values cos

and cos

from (15.9) are then re-

placed by variables {x, y} from (15.7). This is done following the application of

trigonometric Pythagorean theorem of a unit circle {cos

+ sin

= 1} and

{cos

+ sin

= 1} which convert the cosine terms into sines. The resulting

expression has only trigonometric product {2a

cosφ

} on the right-hand-

side. Squaring both sides of the resulting expression and replacing the squared

trigonometric values cos

and cos

, with {x, y} from (15.7) completes the

conversion of (15.6) into algebraic



+ d

y + d

+ d

y + d

x + d

+ d

= 0

x + a

y = 0,

(15.10)

where d

= d

xy + d

+ d

y + d

. The coeﬃcients d

, ..., d

are:

= b

= 2b

+ 2b

= 2b

+ 2b

= 2b

= b

= 2b

+ b

= 2b

+ b

− b

= 2b

+ b

= 2b

+ 2b

= 2b

= b

− b

= 2b

with

= a

+ a

= −2aa

= 2a

= (a

+ a

)

= −2aa

= a

− a

= 2a

The algebraic equation (15.10) indicates that the solution of the nonlinear bending

angle equation (15.6) is given by the intersection of a quartic polynomial (e.g., p.

26) and a straight line (see e.g., Fig. 15.4).

276 15 GNSS environmental monitoring

0 10 20 30 40 50 60

−0.5

0.5

1.5

2.5

3.5

x 10

Graphic solution of occultation bending angle

X,Y

f(X,Y)

quartic polynomial f(X,Y)=0

line aX+bY=0

Figure 15.4. Algebraic curves for the solution of nonlinear system of bending angle

equations

15-32 Algebraic determination of bending angles

15-321 Application of Groebner basis

Denoting the nonlinear system of algebraic (polynomial) equations (15.10) by



:= d

+ d

y + d

+ d

y + d

x + d

+ d

:= a

x + a

(15.11)

reduced Groebner basis (4.38) on p. 45 is computed for x and y as



GroebnerBasis[{f

, f

}, {x, y}, {y}]

GroebnerBasis[{f

, f

}, {x, y}, {x}].

(15.12)

The terms {f

, f

} in (15.12) indicate the polynomials in (15.11), {x, y} the vari-

ables with lexicographic ordering x comes b e fore y, and {y}, {x} the variables to be

eliminated. The ﬁrst expression of (15.12), i.e., GroebnerBasis[{f

, f

}, {x, y}, {y}]

gives a quartic polynomial in x (the ﬁrst expression of 15.13), while the second

expression gives a quartic polynomial in y (the second expression of 15.13). The

results of (15.12) are:



+ h

x + h

= 0

+ g

y + g

= 0,

(15.13)

with the coeﬃcients as

15-3 Refraction (bending) angles 277

= (a

+ a

− a

+ a

− a

)

= (−a

+ a

− a

+ a

)

= (−a

+ a

)

= (−a

+ a

)

= a

and

= (a

+ a

− a

+ a

− a

)

= (a

− a

+ a

− a

)

= (−a

+ a

)

= (a

− a

)

= a

Four solutions are obtained from (15.13) for both x and y using Matlab’s roots com-

mand (e.g., 4.42 on p. 46) as x = roots([

]) and y = roots([

]).

From (15.7) and the roots of (15.13), the required solutions can now be obtained

from



= sin

−1

= sin

−1

(15.14)

The desired bending angle α in Fig. 15.3 is then obtained by ﬁrst computing δ

and δ



= φ

− ψ

= φ

− ψ

(15.15)

leading to



α = δ

+ δ

p =

sinφ

+ r

sinφ

(15.16)

where α(p) is the bending angle and p the impact parameter.

15-322 Sylvester resultants solution

The quartic polynomials (15.13) can also be obtained using Sylvester resultants

technique as follows:

• Step 1: From the nonlinear system of equations (15.10), hide y by treating it

as a constant (i.e., polynomial of degree zero). Using (5.1) and (5.2) on p. 49,

one computes the resultant of a 5 × 5 matrix

Res (f

, f

, y) = det







y 0 0 0

0 a

y 0 0

0 0 a

y 0

0 0 0 a

+ d

y b







, (15.17)

with b

= d

+ d

y, b

= d

+ d

y and b

= d

. The

solution of (15.17) leads to the ﬁrst expression of (15.13).

278 15 GNSS environmental monitoring

• Step 2: Now hide x by treating it as a constant (i.e., polynomial of degree zero)

and compute the resultant of a 5 × 5 matrix as

Res (f

, f

, x) = det







x 0 0 0

0 a

x 0 0

0 0 a

x 0

0 0 0 a

+ d

x c







, (15.18)

with c

= d

+ d

x, c

= d

+ d

x and c

+ d

x. The solution of (15.18) leads to the second

expression of (15.13) from which the bending angles and the impact parameters

can be solved as already discussed.

In summary, the algebraic solution of refraction angles in s pace borne GPS mete-

orology proceeds in ﬁve steps as follows:

Step 1 (coeﬃcients computation):

Using (15.7), compute the coeﬃcients

}

and

}

of the quartic polynomials in (15.13).

Step 2 (solution of variables {x, y}):

Using the coeﬃcients {h

, g

}|i = 1, 2, 3, 4 computed from step 1, obtain the

roots of the univariate polynomials in (15.13) for {x, y}.

Step 3 (determine the angles {φ

, φ

}):

With the admissible values of {x, y} from s tep 2, compute the angles {φ

, φ

}

using (15.14).

Step 4 (obtain the angles {δ

, δ

}):

Using the values of {φ

, φ

} from step 3, compute the angles {δ

, δ

} using

(15.15).

Step 5 (determine the angle α and the impact parameter p):

Finally, the bending angle α and the impact parameter p are computed using

the values of {φ

, φ

} from step 4 in (15.16).

15-4 Algebraic analysis of some CHAMP data

Let us now apply the algebraic algorithm outlined in steps 1 to 5 to assess the

eﬀect of neglecting nonlinearity (i.e., nonlinearity error) in using Newton’s itera-

tive approach, which assumes (15.6) to be linear. In-order c arry out the analysis,

bending angles from CHAMP satellite level 2 data for two satellite occultations

were computed and compared to those obtained from iterative approach in [369].

The occultations were chosen at diﬀerent times of the day and years. Occultation

number 133 of 3rd May 2002 occurred past mid-day at 13:48:36. For this period of

the day, the solar radiation is maximum and so is the ionospheric noise. In contrast,

occultation number 3 of 14th May 2001 occurred past mid-night at 00:39:58.00.

For this period, the solar radiation is minimum and the eﬀect of ionospheric noise

is also minimum.

15-4 Algebraic analysis of some CHAMP data 279

The excess phase length data are smoothed using polyﬁt function of Matlab

software and the resulting doppler shift values for L1 and L2 used together with

(15.7), (15.13) and (15.14) to obtain the angles φ

and φ

. These angles were

then used in (15.16) to compute the refraction angle α and the impact parameter

p (also denoted in this analysis as a). Let us examine in detail the computation

of occultation number 133 of 3rd May 2002 which occurred during the maximum

solar radiation period. The results of occultation number 3 of 14th May 2001 will

thereafter be brieﬂy presented. For occultation number 133 of 3rd May 2002, which

occurred from the time 13:48:36 to 13:49:51.98, the bending angles were computed

using both algebraic and the classical Newton’s (e.g., [369]) algorithms. Since the

algebraic procedure leads to four solutions of (15.13), a criteria for choosing the

admissible solution had to be developed. This was done by using the bending angles

from the classical Newton’s approach as prior information. Time t = 24.66 sec was

randomly chosen and its solutions from both algebraic and classical Newton’s

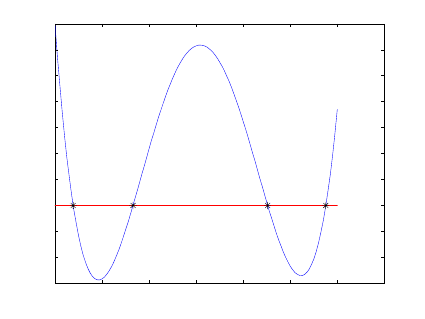
methods for the L1 signal compared. Figures (15.5) and (15.7) show the plot of

the four solutions for x and y computed from (15.13) respectively. These solutions

are converted into angular values {δ

, δ

} using (15.14) and (15.15) resp e ctively

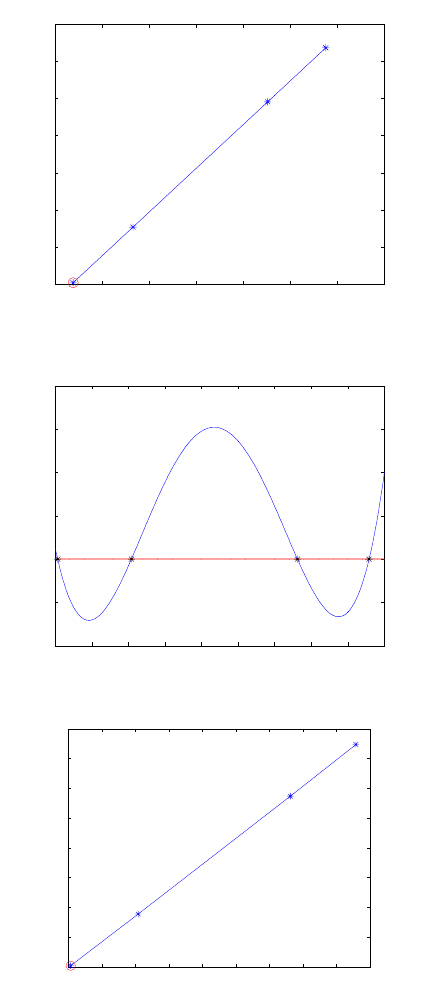
and plotted in Figs. 15.6 and 15.8. From the values of Figs. 15.6 and 15.8, the

smallest values (encircled) were found to be close to those of the classical Newton’s

solution. The algebraic algorithm was then set to select the smallest value amongst

the four solutions. Though Newton’s approach converged after three iterations, a

ﬁxed value of 20 was set for this analysis. The threshold was set such that the

diﬀerence between two consecutive solutions were smaller than 1 × 10

−6

0.2378 0.238 0.2382 0.2384 0.2386 0.2388 0.239 0.2392

−3

−2

−1

x 10

Angle component (dt) at time t=24.66 sec from Quartic h

X+h

X(radians)

h(X)

Figure 15.5. x values for computing the bending angle component δ

for L1 at t =

24.66sec

For the entire occultation, the bending angles {α = δ

+ δ

} for both L1 and

L2 signals were computed using algebraic algorithm and are plotted in Fig. 15.9.

A magniﬁcations of Fig. 15.9 above the height 30 km is plotted in Figs. 15.10 to

show the eﬀect of the residual ionospheric errors on bending angles.

280 15 GNSS environmental monitoring

0.2378 0.238 0.2382 0.2384 0.2386 0.2388 0.239 0.2392

0.01

0.02

0.03

0.04

0.05

0.06

0.07

Selection of the correct angle component dt for L1

X(radians)

dt(degrees)

Figure 15.6. Selection of the admissible x value for computing the component δ

for

L1 at t = 24.66sec

0.9425 0.943 0.9435 0.944 0.9445 0.945 0.9455 0.946 0.9465 0.947

−1

−0.5

0.5

1.5

x 10

Angle component (dl) at time t=24.66 sec from Quartic g

Y+g

Y(radians)

g(Y)

Figure 15.7. y values for computing the bending angle component δ

for L1 at t =

24.66sec

0.9425 0.943 0.9435 0.944 0.9445 0.945 0.9455 0.946 0.9465 0.947

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Selection of the correct angle component dl for L2

Y(radians)

dl(degrees)

Figure 15.8. Selection of the admissible y value for computing the component δ

for

L1 at t = 24.66sec

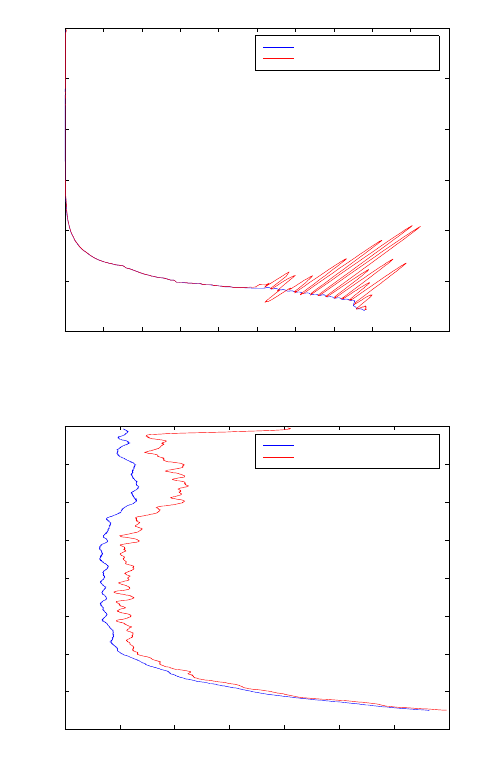
15-4 Algebraic analysis of some CHAMP data 281

0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05

6340

6360

6380

6400

6420

6440

6460

Bending anlges plotted against impact parameter: Algebraic approach

Bending angle(radians)

Impact parameter(km)

Bending angles from L1

Bending angles from L2

Figure 15.9. Bending angles for L1 and L2 from algebraic algorithm

0 0.5 1 1.5 2 2.5 3 3.5

x 10

−4

6380

6390

6400

6410

6420

6430

6440

6450

6460

Bending anlges plotted against impact parameter: Algebraic approach

Bending angle(radians)

Impact parameter(km)

Bending angles from L1

Bending angles from L2

Figure 15.10. Magniﬁcation of the bending angles in Fig. 15.9 above 6380 km

Since bending angle’s data above 40 km are augmented with model values and

those below 5 km are highly inﬂuenced by the presence of water vapour (see e.g.,

Figs. 15.9 and 15.10), we will restricted our analysis to the region between 5-

40 km. Data in this region are normally used directly to derive the atmospheric

proﬁles required for Numerical Weather Prediction (NWP) models . In-order to

assess the eﬀect of nonlinearity assumptions, we subtract the results of the classical

Newton’s approach from those of algebraic approach. This is performed for both

the bending angles α and the impact parameter p. The computations were carried

out separately for both L1 and L2 signals. In-order to compare the results, the

computed diﬀerences are plotted in Figs. 15.11, 15.12, 15.13 and 15.14. In these

Figures, the vertical axes are ﬁxed while the horizontal axes indicate the range