Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

282 15 GNSS environmental monitoring

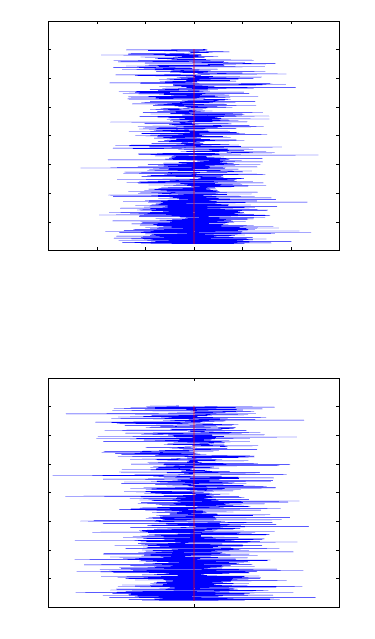
of the computed diﬀerences. In Figures 15.11 and 15.12, the computed diﬀerences

in bending angles due to nonlinearity assumption for L1 are in the range ±6 ×

−5

(degrees) with the maximum absolute value of 5.14 × 10

−5

(degree). For L2,

they are in the range ±5 × 10

−5

(degrees), with the maximum absolute value of

4.85 × 10

−5

(degree). The eﬀects of nonlinearity error on the impact parameters

for L1 are in the range ±1.5 m with the maximum absolute value of 1.444 m, while

those of L2 are in the range ±2 m with the maximum absolute value of 1.534 m.

The large diﬀerences in the impact parameters are due to the large distances

of the GPS satellites (r

> 20, 000 km). They are used in the se cond equation of

(15.16) to compute the impact parameters to which the bending angles are related.

Any small diﬀerence in the computed bending angles due to nonlinearity therefore

contributes signiﬁcantly to the large diﬀerences in the impact parameters. For this

particular occultation therefore, the bending angles of L1 and L2 signals could

probably be related to impact parameters that are oﬀ by up to ±2 m.

−6 −4 −2 0 2 4 6

x 10

−5

Deviation of refraction angle from L1 due to nonlinearity

Height(km)

Deviation(degree)

Figure 15.11. Diﬀerences in bending angles from L1 due to nonlinearity for occultation

133 of 3rd May 2002.

−5 0 5

x 10

−5

Deviation of refraction angle from L2 due to nonlinearity

Height(km)

Deviation(degree)

Figure 15.12. Diﬀerences in bending angles from L2 due to nonlinearity for occultation

133 of 3rd May 2002.

15-4 Algebraic analysis of some CHAMP data 283

−1.5 −1 −0.5 0 0.5 1 1.5

Deviation of impact parameter P from L1 due to nonlinearity

Height(km)

Deviation(m)

Figure 15.13. Diﬀerences in impact parameters from L1 due to nonlinearity for occul-

tation 133 of 3rd May 2002.

−2 −1.5 −1 −0.5 0 0.5 1 1.5

Deviation of impact parameter P from L2 due to nonlinearity

Height(km)

Deviation(m)

Figure 15.14. Diﬀerences in impact parameters from L2 due to nonlinearity for occul-

tation 133 of 3rd May 2002.

In-order to assess the overall eﬀect of nonlinearity on the bending angles, both

bending angles from algebraic and Newton’s procedures have to be related to the

same impact parameters. In this analysis, the bending angles of L2 from algebraic

approach and those of L1 and L2 from Newton’s approach are all matched through

interpolation to the impact parameters P1 of L1 from algebraic approach. The

resulting total bending angles from both algebraic and iterative procedures are

then obtained by the linear correction method of [400] as

α(a) =

(a) − f

(a)

− f

, (15.19)

where f

, f

are the frequencies of L1 and L2 signals respectively and, α

(a) and

(a) the bending angles from L1 and L2 signals respectively. The resulting bend-

ing angles α(a)

from the Newton’s approach and α(a)

from algebraic approach

using (15.19) are plotted in Fig. 15.15. The deviation 5α = α(a)

− α(a)

ob-

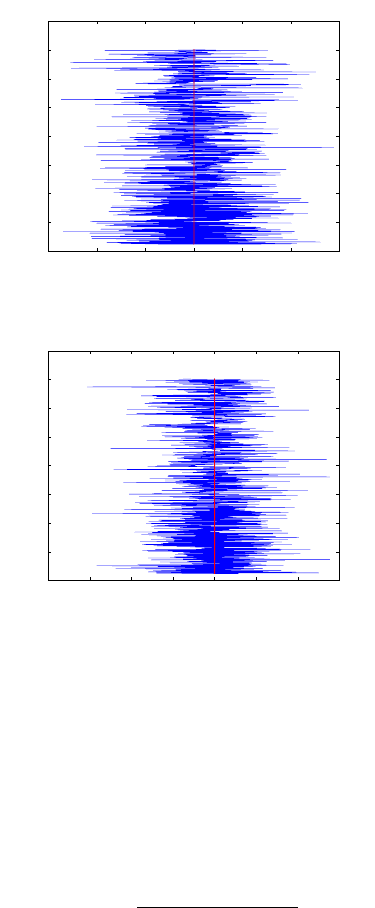
tained are plotted in Fig. 15.16 which indicates the nonlinearity error to increase

with decreasing atmospheric height. From 40km to 15km, the deviation is within

284 15 GNSS environmental monitoring

±2×10

−4

(degrees) but increases to ±7×10

−4

(degrees) for the region below 15km

with the maximum absolute deviation of 0.00069

◦

for this particular occultation.

This maximum absolute error is less than 1%. Vorob’ev and Krasil’nikova [400]

pointed out that the error due to nonlinearity increases downwards to a maximum

of about 2% when the beam perigee is close to the Earth’s ground. The large

diﬀerence in computed bending angles w ith decrease in height is expected as the

region below 5km is aﬀected by the presence of water vapour, and as seen from

Fig. 15.9, the bending angles due to L2 are highly nonlinear.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

Bending anlges from algebraic and iterative approaches

Bending angle(degree)

Height(km)

Bending angles (iterative approach)

Bending angles (algebraic approach)

Figure 15.15. Bending angles from iterative and algebraic algorithms matched to the

same impact parameters for occultation 133 of 3rd May 2002.

−6 −4 −2 0 2 4 6 8

x 10

−4

Deviation of bending anlges due to nonlinearity assumption: 03−05−2002

Bending angle(degree)

Height(km)

Figure 15.16. Diﬀerences of computed bending angles due to nonlinearity for occultation

133 of 3rd May 2002.

15-4 Algebraic analysis of some CHAMP data 285

The algebraic approach was next used to compute the bending angles of occul-

tation number 3 of 14th May 2001 which occurred past mid-night at 00:39:58.00.

For this period, as stated earlier, the solar radiation is minimum and the eﬀect of

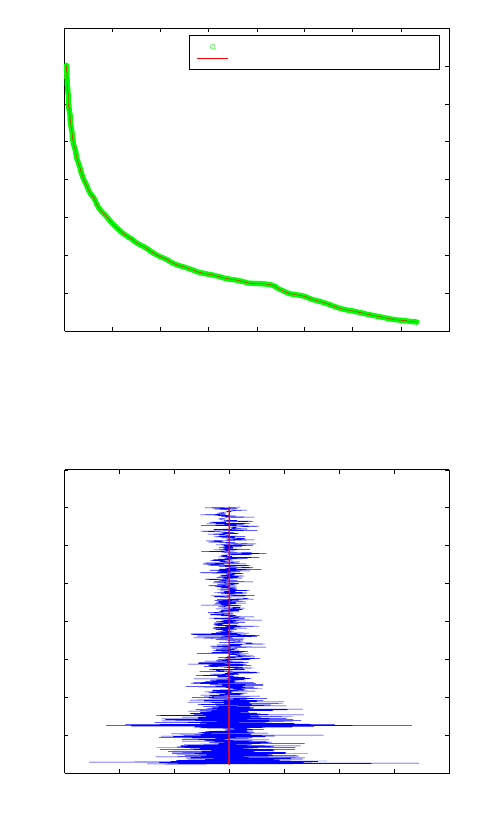
ionospheric noise is also minimum. The results from this occultation show the dif-

ferences in bending angles from the algebraic and Newton’s methods to be smaller

(see Fig. 15.17) compared to those of s olar maximum period. The maximum ab-

solute diﬀerence value for b ending angles was 0.00001

◦

. For the computed impact

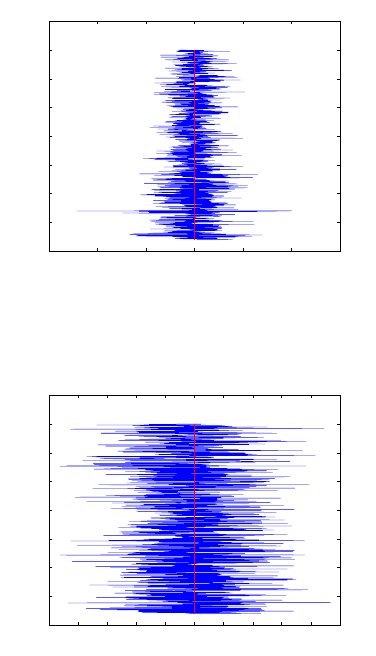
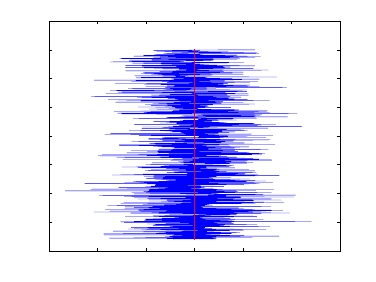
parameters, the diﬀerences were in the range ±5 cm for L1 signal (Fig. 15.18) and

±6 cm for L2 (Fig. 15.19). The maximum absolute values were 4 cm and 5 cm re-

spectively. In comparison to the results of occultation 133 of 3rd May 2002, the

results of occultation 3 of 14th May 2001 indicate the eﬀect of ionospheric noise

during low solar radiation period to be less. The ionospheric noise could there-

fore increase the errors due to nonlinearity. In [36], further analysis of nonlinear

bending angles have shown that there could exist other factors that inﬂuence the

nonlinearity error other than the ionospheric noise.

−1.5 −1 −0.5 0 0.5 1 1.5

x 10

−5

Deviation of bending anlges due to nonlinearity assumption: 14−05−2001

Bending angle(degree)

Height(km)

Figure 15.17. Diﬀerences in bending angles due to nonlinearity for occultation number

3 of 14th May 2001.

−0.05 −0.04 −0.03 −0.02 −0.01 0 0.01 0.02 0.03 0.04 0.05

Deviation of impact parameter P from L1 due to nonlinearity: 14−05−2001

Deviation(m)

Height(km)

Figure 15.18. Diﬀerences in impact parameters from L1 due to nonlinearity for occul-

tation number 3 of 14th May 2001

286 15 GNSS environmental monitoring

−0.06 −0.04 −0.02 0 0.02 0.04 0.06

Deviation of impact parameter P from L2 due to nonlinearity: 14−05−2001

Deviation(m)

Height(km)

Figure 15.19. Diﬀerences in impact parameters from L2 due to nonlinearity for occul-

tation number 3 of 14th May 2001

15-5 Concluding remarks

The new concept of GPS meteorology and its application to environmental moni-

toring is still new and an active area of research. The data that has been collected

so far have unearthed several atmospheric properties that were hitherto diﬃcult

to fathom. The new technique clearly promises to contribute signiﬁcantly and

enormously to environmental and atmospheric studies. When the life span of the

various missions (e.g., CHAMP, GRACE) will have reached, thousands of data will

have been collected which will help unravel some of the hidden and complicated

atmospheric and environmental phenomenon. Satellite missions such as EQUARS

will contribute valuable equatorial data that have long been elusive due to poor

radiosonde coverage. From the analysis of water vapour trappe d in the atmosphere

and the tropopause temperature, global warming studies will be enhanced a great

deal.

We have also successfully presented an independent algebraic algorithm for

solving the system of nonlinear bending angles for space borne GPS meteorology

and shown that nonlinearity correction should be taken into account if the accuracy

of the desired proﬁles are to be achieved to 1%. In particular, it has been high-

lighted how the nonlinearity errors in bending angles contribute to errors in the

impact parameters to which the bending angles are related. Occultation number

133 of 3rd May 2002 which occurred past noon and occultation number 3 of 14th

May 2001 which occurred past mid-night indicated the signiﬁcance of ionospheric

noise on nonlinearity error. When ionospheric noise is minimum, e.g., during mid-

night, the computed diﬀerences in bending angles between the two procedures

are almost negligible. During maximum solar radiation in the afternoons with

increased ionospheric noise, the computed diﬀerences in bending angles between

algebraic and classical Newton’s methods increases.

The proposed algebraic method could therefore be used to control the results of

the classical Newton’s method especially when the ionospheric noise is suspected

to be great, e.g., for occultations that occur during maximum solar radiation pe-

riods. The hurdle that must be overcome however is to concretely identify the

15-5 Concluding remarks 287

criteria for selecting the admissible solution amongst the four algebraic solutions.

In this analysis, the smallest values amongst the four algebraic solutions turned

out to be the admissible in comparison with values of the classical Newton’s ap-

proach. Whether this applies in general is still subject to investigation. In terms of

computing time, the algebraic approach would probably have an advantage over

the classical Newton’s iterative procedure in cases where thousands of occultations

are to be processed. For single occultations however, the classical Newton’ s ap-

proach generally converges after few iterations and as such, the advantage of the

algebraic approach in light of modern computers may not be so signiﬁcant. For

further literature on GPS meteorology, we refer to [13, 343].

16 Algebraic diagnosis of outliers

16-1 Outliers in observation samples

In Chap. 7, we introduced parameter estimation from observational data sample

and deﬁned the models applicable to linear and nonlinear cases. In-order for the

estimates to be meaningful however;

(a) proper ﬁeld observations must be carried out to minimize chances of gross

errors,

(b) the observed data sample must be processed to minimize or eliminate the

eﬀects of systematic errors,

applied.

Despite the care taken during observation period and the improved models used

to correct systematic errors, observations may still be contaminated with outliers

or gross errors. Outliers are those observations that are inconsistent with the rest

of the observation sample. They often degrade the quality of the estimated pa-

rameters and render them unreliable for any meaningful inferences (deductions).

Outliers ﬁnd their way into observational data sample through:

• Miscopying during data entry, i.e., a wrong value can be entered during data

input into the computer or other processing machines.

• Misreading during observation period, e.g., number 6 can erroneously be read

as 9.

• Instrumental errors (e.g., problems with centering, vertical and horizontal cir-

cles, unstable tripod stands etc.)

• Rounding and truncation errors (e.g., during data processing)

• Poor models applied to correct systematic errors and estimate parameters (e.g.,

a linear model may be assumed where a nonlinear model could be suitable).

This error is also common during data smoothing where a linear ﬁt is used

where actually a cubic ﬁt could have been most suitable etc.

• Key punch errors during data input etc.

A special problem faced by users while dealing with outliers is the basis on which to

discard observations from a set of data on the grounds that they are contaminated

with outliers.

The least squares method used to estimate parameters assume the observa-

tional errors to be independent and normally distributed. In the presence of gross

errors in the observational data sample, these assumptions are violated and hence

render the estimators, such as least squares, ineﬀective. Earlier attempts to cir-

cumvent the problem of outlier involved procedures that would ﬁrst detect and

isolate the outliers before adjusting the remaining data sample. Such procedures

were both statistical as seen in the works of [45, 46, 47, 304, 420, 421, 422], and

non statistical e.g., [219]. Other outlier detection procedures have been presented

by [4, 7].

J.L. Awange et al., Algebraic Geodesy and Geoinformatics, 2nd ed.,

DOI 10.1007/978-3-642-12124-1 16,

 Springer-Verlag Berlin Heidelberg 2010

290 16 Algebraic diagnosis of outliers

The detection and isolation approach to the outlier problem comes with its

own shortcoming. On one hand, there exists the danger of false deletion and false

retention of the assumed outliers. On the other hand, there exists the problem that

the detection techniques are based on the residuals computed initially using the

least squares method which has the tendency of masking the outliers by pulling

their residuals closer to the regression ﬁt. This makes the detection of outliers

diﬃcult. These setbacks had been recognized by the father of robust statistics P. J.

Huber [232], [233, p. 5] and also [205, pp. 30–31] who suggested that the best option

to deal with the outlier problem was to use robust estimation procedures. Such

procedures would proceed safely despite the presence of outliers, isolate them and

give admissible estimates that could have been achieved in the absence of outliers

(i.e., if underlying distribution was normal). Following the fundamental paper by

P. J. Huber in 1964 [231] and [233], several robust estimation procedures have

been put forward that revolve around the robust M-estimators, L-estimators and

R-estimators. In geodesy and geoinformatics, use of robust estimation techniques

to estimate parameters has been presented e.g., in [5, 19, 20, 108, 196, 244, 246,

247, 306, 351, 422, 425, 426, 428] among others.

In this chapter, we present a non-statistical algebraic approach to outlier di-

agnosis that uses the Gauss-Jacobi combinatorial algorithm presented in Chap. 7.

The combinatorial solutions are analyzed and those containing falsiﬁed observa-

tions identiﬁed. In-order to test the capability of the algorithm to diagnose outliers,

we inject outliers of diﬀerent magnitudes and signs on planar ranging and GPS

pseudo-ranging problems. The algebraic approach is then employed to diagnose

the outlying observations.

For GPS pseudo-range observations, the case of multipath eﬀect is considered.

Multipath is the error that occurs when the GPS signal is reﬂected (mostly by

reﬂecting surfaces in built up areas) towards GPS receivers, rather than travel-

ling directly to the receiver. This error still remains a menace which hinders full

exploitation of the GPS system. Whereas other GPS observational errors such as

ionospheric and atmospheric refractions can be modelled, the error due to mul-

tipath still poses some diﬃculties in being contained thus necessitating a search

for procedures that can deal with it. In proposing procedures that can deal with

the error due to multipath, [416] have suggested the use of robust estimation ap-

proach that is based on iteratively weighted least squares (e.g., a generalization

of the Danish method to heterogeneous and correlated observations). Awange [18]

prop os ed the use of algebraic deterministic approach to diagnose outliers of type

multipath.

16-2 Algebraic diagnosis of outliers

Let us illustrate by means of a simple linear example how the algebraic algorithm

diagnoses outliers.

Example 16.1 (Outlier diagnosis using Gauss-Jacobi combinatorial algorithm). Con-

sider a case where three linear equations have been given for the purpose of solving

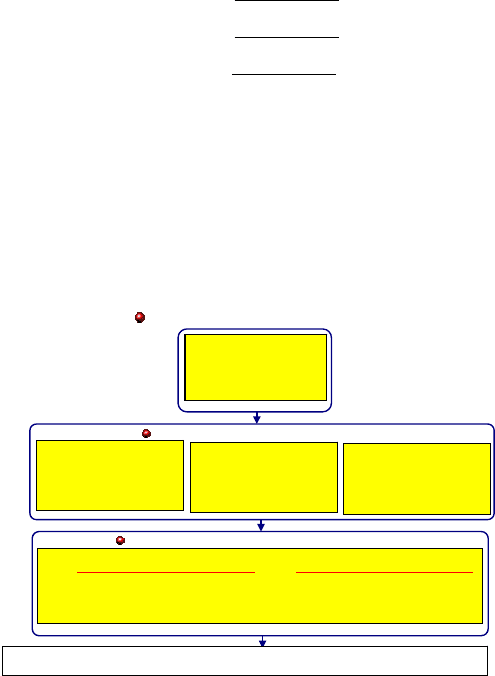
16-2 Algebraic diagnosis of outliers 291

the two unknowns(x, y) in Fig. 16.1. Three pos sible combinations, each containing

two equations necessary for solving the two unknowns, can be formed as shown in

the box labelled “combination”. Each of these systems of two linear equations is

either solved by substitution, graphically or matrix inversion to give three pairs of

solutions {x

1,2

, y

1,2

}, {x

2,3

, y

2,3

} and {x

1,3

, y

1,3

}. The ﬁnal step involves adjusting

these pseudo-observations {x

1,2

, y

1,2

, x

2,3

, y

2,3

, x

1,3

, y

1,3

} as indicated in the box

labelled “adjustment of the combinatorial subsets solutions”. The weight matrix Σ

or the weight elements {π

1,2

, π

2,3

, π

1,3

} are obtained via nonlinear error/variance-

covariance propagation. Assuming now that observation y

is contaminated by

gross error ∂y, then the ﬁrst two combinatorial sets of the system of equations

containing observation y

will have their results {x

1,2

, y

1,2

}, {x

1,3

, y

1,3

} changed

to {x

∗

1,2

, y

∗

1,2

}, {x

∗

1,3

, y

∗

1,3

} respectively because of the change of observation y

+ ∂y). The third combination set {x

2,3

, y

2,3

} without observation (y

+ ∂y)

remains unchanged. If one computes the combinatorial positional norms







∗2

1,2

+ y

∗2

1,2

)

∗2

1,3

+ y

∗2

1,3

)

2,3

+ y

2,3

and subtract them from the norms of the adjusted positional values, median or a

priori values (say from maps), one can analyze the deviations to obtain the falsiﬁed

observation y

which is common in the ﬁrst two sets. It will be noticed that the

deviation of the ﬁrst two sets containing the contaminated value is larger than the

uncontaminated set. The median is here used as opp osed to the mean as it is less

sensitive to extreme scores.

Forasystemoflinearequations

+ − =

111

222

333

ax by y

⎧

⎫

+ − =

⎪⎪

⎨⎬

⎪⎪

+ − =

⎪⎪

⎩⎭

1,2 1,2

111

222

ax by y

ax y

⎧

⎫

+ − =

⎪⎪

⎨⎬

⎪⎪

+ − =

⎪⎪

⎩⎭

1,3 1,3

111

333

ax by y

ax y

⎧

⎫

+ − =

⎪⎪

⎨⎬

⎪⎪

+ − =

⎪⎪

⎩⎭

2,3 2,3

222

333

ax by y

ax y

Form3combinatorialsolutions

Adjustthecombinatorialsubsetsolutions

1,2 1,2 1,3 1,3 2,3 2,3 1,2 1,2 1,3 1,3 2,3 2,3

1,2 1,3 2,3 1,2 1,3 2,3

11 1

( Σ ) Σ

xxx yyy

πππ πππ

−− −

⎧⎫

⎪⎪

++ ++

⎪⎪

⎨⎬

⎪⎪

++ ++

⎪⎪

⎩⎭

′′

=ξ AAAy



Subtractthecombinatorialsolutionsfromtheadjustedtodetect outliers

Figure 16.1. Algebraic outlier diagnosis steps

292 16 Algebraic diagnosis of outliers

The program operates in the following steps:

Step 1: Given an overdetermined system with n observations in m unknowns, k

combinations are formed using (7.28) on p. 93.

Step 2: Each of the minimal combination is solved in closed form using either

Groebner basis or polynomial res ultant algebraic technique of Chaps. 4 or 5.

From the combinatorial solutions, compute the positional norm.

Step 3: Perform the nonlinear error/variance-covariance propagation to obtain

the weight matrix of the pseudo-observations resulting from step 2.

Step 4: Using these pseudo-observations and the weight matrix from step 3, per-

form an adjustment using linear Gauss-Markov model (7.12) on p. 87.

Step 5: Compute the adjusted barycentric coordinate values together with its

positional norm and the median positional norm from step 2. Subtract these

positional norms from those of the combinatorial solutions to diagnose outliers

from the deviations.

16-21 Outlier diagnosis in planar ranging

In Sect. 12-3 of Chap. 12, we discussed the planar ranging problem and presented

the solution to the overdetermined case. We demonstrated by means of Example

12.4 on p. 198 how the position of unknown station could be obtained from distance

measurements to more than two s tations. In this section, we use the same example

to demonstrate how the algebraic combinatorial algorithm can be used to diagnose

outliers. From observational data of the overdetermined planar ranging problem

of [237] given in Table 12.11 on p. 198, the position of the unknown station is

determined. The algorithm is then applied to diagnose outlying observations. Let

us consider three cases as follow s; ﬁrst, the algorithm is subjected to outlier free

observations and used to compute the positional norms. Next, an outlier of 0.95 m

is injected to the distance observation to station 2 and the algorithm applied to

diagnose that particular observation. Finally, the distance observed to station 4 is

considered to have been miss-booked with 6 typed as 9, thus leading to an error

of 3 m.

Example 16.2 (Outlier free observations). From the values of Table 12.11 and using

(7.28) on p. 93, 6 combinations, each consisting of two observation equations are

formed. The aim is to obtain the unknown position from the nonlinear ranging

observations equations. From the computed positions in step 2, the positional

norms are given by

+ Y

i=1, . . . ,6

, (16.1)

where (X

, Y

) |

i=1, . . . ,6

are the two-dimensional geocentric coordinates of the un-

known station computed from each combinatorial pair. Table 16.1 indicates the

combinations, their computed positional norms, and deviations from the norm of

the adjusted value (48941.769 m) from step 4. The results are for the case of outlier

free observations. These deviations are plotted against combinatorial numbers in

Fig. 16.2.