Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics
Подождите немного. Документ загружается.


314 17 Datum transformation problems
J
y
=
∂f
1
∂a
1
∂f
1
∂b
1
∂f
1
∂c
1
∂f
1
∂a
2
∂f
1
∂b
2
∂f
1
∂c
2
∂f
1
∂a
3
. . . . . . . . . .
∂f
1
∂Z
3
∂f
2
∂a
1
∂f
2
∂b
1
∂f
2
∂c
1
∂f
2
∂a
2
∂f
2
∂b
2
∂f
2
∂c
2
∂f
2
∂a
3
. . . . . . . . . .
∂f
2
∂Z
3
∂f
3
∂a
1
∂f
3
∂b
1
∂f
3
∂c
1
∂f
3
∂a
2
∂f
3
∂b
2
∂f
3
∂c
2
∂f
3
∂a
3
. . . . . . . . . .
∂f
3
∂Z
3
∂f
4
∂a
1
∂f
4
∂b
1
∂f
4
∂c
1
∂f
4
∂a
2
∂f
4
∂b
2
∂f
4
∂c
2
∂f
4
∂a
3
. . . . . . . . . .
∂f
4
∂Z
3
∂f
5
∂a
1
∂f
5
∂b
1
∂f
5
∂c
1
∂f
5
∂a
2
∂f
5
∂b
2
∂f
5
∂c
2
∂f
5
∂a
3
. . . . . . . . . .
∂f
5
∂Z
3
∂f
6
∂a
1
∂f
6
∂b
1
∂f
6
∂c
1
∂f
6
∂a
2
∂f
6
∂b
2
∂f
6
∂c
2
∂f
6
∂a
3
. . . . . . . . . .
∂f
6
∂Z
3
∂f
7
∂a
1
∂f
7
∂b
1
∂f
7
∂c
1
∂f
7
∂a
2
∂f
7
∂b
2
∂f
7
∂c
2
∂f
7
∂a
3
. . . . . . . . . .
∂f
7
∂Z
3
, (17.23)
where the doted points in J
y
represent the partial derivatives of (17.15) with
respect to
{b
3
, c
3
, X
1
, Y
1
, Z
1
, X
2
, Y
2
, Z
2
, X
3
, Y
3
}.
From the disp e rsion Σ
y
of the vector of observations y and with (17.22) and
(17.23) forming J = J
−1
x
J
y
, the dispersion matrix Σ
x
is then obtained using
(7.31). Finally, we obtained the dispersion matrix Σ from (7.33) on p. 94. The
solution is performed stepwise as discussed on p. 259. There exist two possibilities
of using the combinatorial algorithm. These are:
(1) Forming combinations of the given coordinates, each minimal set comprising
3 points. Given n number of points in both systems, combinations can be
formed from (7.28) on p. 93, each set containing m = 3 points. For each
combination, the desired transformation parameters are computed using the
explicit formulae in [23, Boxes 2-2 and 2-3] or [37, Appendices A and B]. The
resulting combinatorial solutions are then adjusted using the special linear
Gauss-Markov model.
(2) Alternatively, instead of forming combinations from points alone and solving
as in (1) above, combinations are formed both for the points and also from the
9 equations in (17.15). In this case, e ach minimal combinatorial in points will
have three stations from which a further combinatorial in terms of equations
are formed. From the 9 equations in (17.15), combinations are formed with a
minimum of seven equations per set. The solution of the seven equations of
each combinatorial set delivers equations of the form in [23, Boxes 2-2 and
2-3]. Once the solution is completed for a minimum combinatorial set for three
points, the proce dure is repeated for other points until all the combinations
have been solved. The resulting combinatorial solutions are then adjusted using
17-2 Algebraic solution of the 7-parameter transformation problem 315
the special linear Gauss-Markov model as already explained. This approach is
labour intensive, but may offer improved accuracy as compared to the approach
in (1) as all the available information is exploited. We leave it as an exercise
for an interested reader.
Example 17.2 (Computation of transformation parameters using Gauss-Jacobi com-
binatorial algorithm). We repeat Example 17.1 by computing the 7 transforma-
tion parameters for the overdetermined case using the combinatorial algorithm.
All 7 points of Tables 17.1 and 17.2 are used, unlike in Example 17.1 where only
three points were used (e.g., the minimal case). The computed transformation
parameters are presented in Table 17.7. In order to check the accuracy of these
parameters, they are used to transform the Cartesian coordinates from the local
reference system in Table 17.1 to WGS-84. Table 17.8 gives the residuals computed
by subtracting the transformed values from the actual GPS coordinates of Table
17.2. Table 17.9 gives for comparison purpos es the residuals obtained using least
squares method. The residuals from both procedures are of the same magnitude.
We also compute the residual norm (square root of the sum of squares of residu-
als) and present them in Table 17.10. The computed norms from the combinatorial
solutions are some what better than those of the linearized least squares solutions.
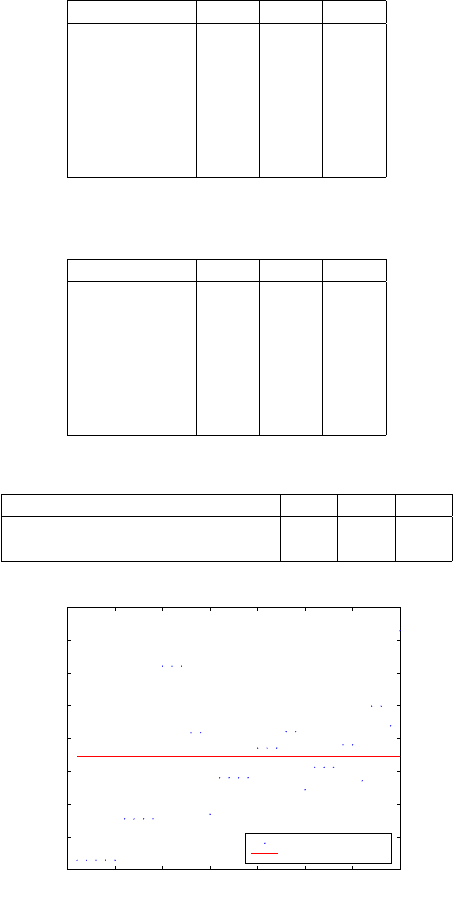
Figure 17.1 presents the scatter of the computed 36 minimal combinatorial solu-
tions of scale indicated by doted points (•) around the adjusted value indicated
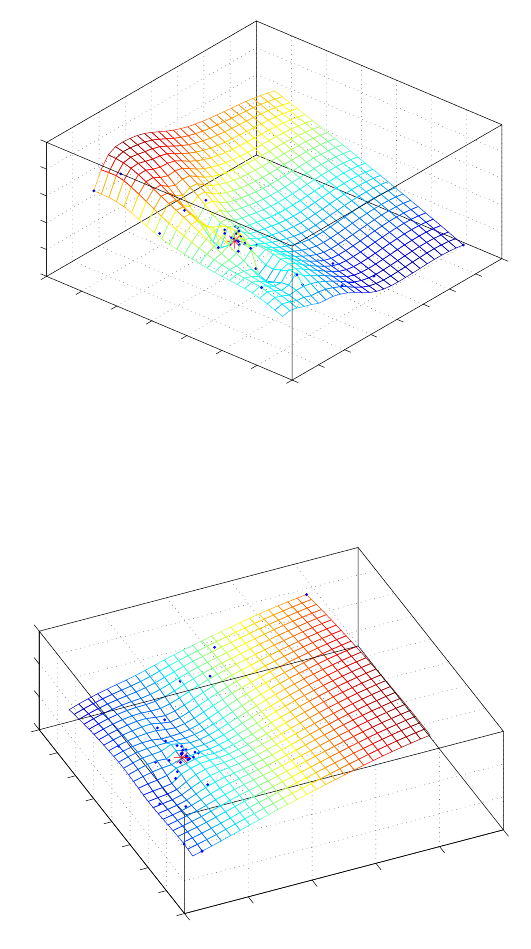
by a line (−). Figures 17.2 and 17.3 plot the scatter of the computed 36 minimal
combinatorial solutions of the translation and rotation parameters indicated by
doted points (•) around the adjusted values indicated by stars (?).
Table 17.7. Gauss-Jacobi combinatorial’s 7 transformation parameters
Transformation parameter Value Root-mean-square unit
Scale k − 1 4.92377597 0.350619414 [ppm]
Rotation X
1
(a) -0.98105498” 0.040968549 [“]
Rotation X
2
(b) 0.68869774” 0.047458707 [“]
Rotation X
3
(c) 0.96671738” 0.044697434 [“]
Translation ∆X 639.9785 2.4280 [m]
Translation ∆Y 68.1548 3.0123 [m]
Translation ∆Z 423.7320 2.7923 [m]
316 17 Datum transformation problems
Table 17.8. Residuals of the transformed Cartesian coordinates of System A (Table
17.1) into System B using the parameters in Table 17.7
Site X(m) Y (m) Z(m)
Solitude 0.0739 0.1381 0.1397
Buo ch Zeil 0.0328 -0.0301 0.0095
Hohenneuffen -0.0297 -0.0687 -0.0020
Kuelenberg 0.0246 -0.0347 -0.0793
Ex Mergelaec -0.1405 0.0228 -0.0148
Ex Hof Asperg -0.0477 0.0116 -0.0599
Ex Keisersbach -0.0673 0.0335 -0.0070
Table 17.9. Residuals of the transformed Cartesian coordinates of System A (Table
17.1) into System B using the parameters computed by a least squares method
Site X(m) Y (m) Z(m)
Solitude 0.0940 0.1351 0.1402
Buo ch Zeil 0.0588 -0.0497 0.0137
Hohenneuffen -0.0399 -0.0879 -0.0081
Kuelenberg 0.0202 -0.0220 -0.0874
Ex Mergelaec -0.0919 0.0139 -0.0055
Ex Hof Asperg -0.0118 0.0065 -0.0546
Ex Keisersbach -0.0294 0.0041 -0.0017
Table 17.10. Computed residual norms
Metho d X(m) Y (m) Z(m)
Linearized Least Squares Solution 0.1541 0.1708 0.1748
Gauss-Jacobi Combinatorial 0.1859 0.1664 0.1725
0 5 10 15 20 25 30 35
−2
0
2
4
6
8
10
12
14
x 10
−6
Scale combinatorial scatter around the adjusted value
Combinatorial No.
Scale (ppm)
scatter in scale
Adjusted mean value
Figure 17.1. Scatter of the computed 36 minimal combinatorial values of scale around
the adjusted value
17-2 Algebraic solution of the 7-parameter transformation problem 317
−150
−100
−50
0
50
100
150
200
−200
−100
0
100
200
300
400
500
60
0
−200
−100
0
100
200
300
Y(m)+60(m)
3d−plot of translation combinatorial scatter around the adjusted values
X(m)+600(m)
Z(m)+400(m)
Figure 17.2. Scatter of the 36 computed translations around the adjusted values
−2
0
−15
−10
−5
0
5
−8
−6
−4
−2
0
2
4
6
8
−10
0
10
20
a(")
3d−plot of rotation combinatorial scatter around the adjusted values
b(")
c(")
Figure 17.3. Scatter of the 36 computed rotations around the adjusted values (dots)
and (stars)
318 17 Datum transformation problems
17-3 The 9-parameter (affine) datum transformation
Due to the distortions between the traditional terrestrial and GPS derived net-
works, the 7-parameter similarity transformations in some cases may not offer
satisfactory precision. For example, transforming GPS global coordinates to the
local Hungarian system with similarity transformation gives 0.5 m maximal resid-
uals, see, e.g., Papp and Sz˝ucs [326]. To reduce the remaining residuals, other
transformation models with more paramete rs can be used.
The 9-parameter affine transformation is not only a logical extension but even
a generalization of the 7-parameter similarity model. This transformation is the
modification of the Helmert C
7
(3,3) transformation, where 3 different scales are
used in the corresponding coordinate axes instead of one scale factor. In the case
of the 3 scale parameters being equal, the model reverts back to the similarity
transformation.
The solution of the 9-parameter model was achieved by Sp¨ath [368] using the
numerical minimization technique of the residuum vector, as well as by Papp and
Sz˝ucs [326] who used the linearized least squares method. Watson [403] pointed
out that the Gauss-Newton method or its variants can be easily implemented for
the 9-parameter problem using separation of variables and iteration with respect
to the rotation parameters alone, while other parameters can be calculated via
a simple linear least squares solution. The Watson [403] m ethod is analogous to
other methods for separated least square problems, which goes back at least to
Golub and Pereyra [152].
The 9-parameter affine transformation is also included in some co ordinate-
transformation software developed following requests from GPS users (see e.g. [295,
143]). To determine the 9 parameters of the 3D affine transformation, a minimum of
3 points with known coordinates (x
i
, y
i
, z
i
, X
i
, Y
i
, Z
i
) in both systems is required.
This is the so-called 3-point problem. However, in geodesy and geoinformatics,
N > 3 known points are usually available.
The N -point problem is basically an overdetermined problem and because of
the size of real world problems, the Gauss-Jacobi combinatorial solution becomes
inadequate. In what follows, an alternative ALESS method is applied to solve for
the 9 parameters of the overdetermined affine model.
Definition of the problem
The 3D affine transformation is the generalization of the C
7
(3,3) Helmert trans-
formation, using three different scale (s
1
, s
2
, s
3
) parameters instead of a single one.
Consider (17.24)
x
i
y
i
z
i
= WR
X
i
Y
i
Z
i
+
X
0
Y
0
Z
0
, (17.24)
where W is the scale matrix, X
0
, Y
0
, Z
0
the translation parameters, R the rotation
matrix, and x
i
, y
i
, z
i
and X
i
, Y
i
, Z
i
are the coordinates of the points in the two

17-3 The 9-parameter (affine) datum transformation 319
coordinate systems. For such a case (cf x
1
in Eqn. 17.1), the scale factors can be
modeled by a diagonal matrix
W =
s
1
0 0
0 s
2
0
0 0 s
3
. (17.25)
Instead of using the traditionally simplified Cardan angles representation of R
(see, e.g., Papp and Sz˝ucs [326]), we will use the same rotation matrix as in the
case of the 7-parameter transformation, expressed by a skew-symmetric matrix,
facilitating the symbolic-numeric solution of the problem without simplifications.
The rotation matrix
R = (I
3
− S)
−1
(I
3
+ S), (17.26)
where S is the skew-symmetric matrix was given in 17.4 and parameterized using
a, b and c as
R =
1+a
2
−b
2
−c
2
1+a
2
+b
2
+c
2
2(ab−c)
1+a
2
+b
2
+c
2
2(b+ac)
1+a
2
+b
2
+c
2
2(ab+c)
1+a
2
+b
2
+c
2
1−a
2
+b
2
−c
2
1+a
2
+b
2
+c
2
−
2(a−bc)
1+a
2
+b
2
+c
2
2(−b+ac)
1+a
2
+b
2
+c
2
2(a+bc)
1+a
2
+b
2
+c
2
1−a
2
−b
2
+c
2
1+a
2
+b
2
+c
2
, (17.27)
for which the orthogonality relation holds such that RR
T
is an identity matrix.
The axial rotation angles (Cardan angles) can be calculated also from the rotation
matrix R in 17.7. Furthermore, instead of the scale parameters (s
1
, s
2
, s
3
), the
inverse values of the sc ale parameters (σ
1
, σ
2
, σ
3
) can be used to obtain simplified
equations.
Let us call σ
i
= 1/s
i
and introduce Ω = W
−1
Ω =
σ
1
0 0
0 σ
2
0
0 0 σ
3
. (17.28)
Expressing the rotation matrix with the skew-symmetric matrix and using the
inverse of the scale matrix (Ω), Eq. (17.24) can be written in the form,
x
i
y
i
z
i
= Ω
−1
(I
3
− S)
−1
(I
3
+ S)
X
i
Y
i
Z
i
+
X
0
Y
0
Z
0
. (17.29)
Multiplying both sides by (I
3
− S)Ω and rearranging the equation leads to
0
0
0
= (I
3
− S)Ω
x
i
y
i
z
i
− (I
3
+ S)
X
i
Y
i
Z
i
− (I
3
− S)Ω
X
0
Y
0
Z
0
. (17.30)
Finally, substituting Ω and S in to Eq. (17.30) gives,
320 17 Datum transformation problems
0
0
0
=
1 c −b
−c 1 a
b −a 1
σ
1
0 0
0 σ
2
0
0 0 σ
3
x
i
y
i
z
i
−
1 −c b
c 1 −a
−b a 1
X
i
Y
i
Z
i
−
1 c −b
−c 1 a
b −a 1
σ
1
0 0
0 σ
2
0
0 0 σ
3
X
0
Y
0
Z
0
,
(17.31)
where the unknown parameters are the three rotation parameters (a, b, c), the
three translation parameters (X
0
, Y
0
, Z
0
) and the three inverse scale parameters
(σ
1
, σ
2
, σ
3
).
17-4 Algebraic solution of the 9-parameter transformation
17-41 The 3-point affine transformation problem
For the determination of the 9 parameters (a, b, c, X
0
, Y
0
, Z
0
, s
1
, s
2
, s
3
) of
the 3D affine transformation, we need 9 equations. According to Eq. (17.31), for
one point with known coordinates in both coordinate systems, we can write three
equations. For the determination of all parameters therefore, 3 non-collinear points
with known coordinates are needed. In this case the 9 equations, which give a
nonlinear system (f
i
= 0) (see Eq.(17.32)) are written as
f
1
= −X
1
+ cY
1
− bZ
1
+ x
1
σ
1
− X
0
σ
1
+ cy
1
σ
2
− cY
0
σ
2
− bz
1
σ
3
+ bZ
0
σ
3
f
2
= −cX
1
− Y
1
+ aZ
1
− cx
1
σ
1
+ cX
0
σ
1
+ y
1
σ
2
− Y
0
σ
2
+ az
1
σ
3
− aZ
0
σ
3
f
3
= bX
1
− aY
1
− Z
1
+ bx
1
σ
1
− bX
0
σ
1
− ay
1
σ
2
+ aY
0
σ
2
+ z
1
σ
3
− Z
0
σ
3
f
4
= −X
2
+ cY
2
− bZ
2
+ x
2
σ
1
− X
0
σ
1
+ cy
2
σ
2
− cY
0
σ
2
− bz
2
σ
3
+ bZ
0
σ
3
f
5
= −cX
2
− Y
2
+ aZ
2
− cx
2
σ
1
+ cX
0
σ
1
+ y
2
σ
2
− Y
0
σ
2
+ az
2
σ
3
− aZ
0
σ
3
f
6
= bX
2
− aY
2
− Z
2
+ bx
2
σ
1
− bX
0
σ
1
− ay
2
σ
2
+ aY
0
σ
2
+ z
2
σ
3
− Z
0
σ
3
f
7
= −X
3
+ cY
3
− bZ
3
+ x
3
σ
1
− X
0
σ
1
+ cy
3
σ
2
− cY
0
σ
2
− bz
3
σ
3
+ bZ
0
σ
3
f
8
= −cX
3
− Y
3
+ aZ
3
− cx
3
σ
1
+ cX
0
σ
1
+ y
3
σ
2
− Y
0
σ
2
+ az
3
σ
3
− aZ
0
σ
3
f
9
= bX
3
− aY
3
− Z
3
+ bx
3
σ
1
− bX
0
σ
1
− ay
3
σ
2
+ aY
0
σ
2
+ z
3
σ
3
− Z
0
σ
3
.
(17.32)
To solve this system of equations, different symbolical and numerical methods
can be used. In what follows, symbolic solution of this problem using the Dixon
resultant and Groebner basis are presented, as was done previously for the 7-
parameter problem.
17-411 Simplifications for the symbolic solution
Similar to the C
7
(3, 3) problem, we can reduce the system of equation (17.32) by
differencing the equations. In this way, the translation parameters (X
0
, Y
0
, Z
0
)
17-4 Algebraic solution of the 9-parameter transformation 321
can b e eliminated. The elimination of the translation parameters can be done by
subtractions
g
1
= f
1
− f
7
= − X
1
+ X
3
+ (x
1
− x
3
)σ
1
+ c(Y
1
− Y
3
+ (y
1
− y
3
)σ
2
)
− b(Z
1
− Z
3
+ (z
1
− z
3
)σ
3
)
g
2
= f
4
− f
7
= − X
2
+ X
3
+ (x
2
− x
3
)σ
1
+ c(Y
2
− Y
3
+ (y
2
− y
3
)σ
2
)
− b(Z
2
− Z
3
+ (z
2
− z
3
)σ
3
)
g
3
= f
2
− f
8
= − Y
1
+ Y
3
− c(X
1
− X
3
+ (x
1
− x
3
)σ
1
) + (y
1
− y
3
)σ
2
+ a(Z
1
− Z
3
+ (z
1
− z
3
)σ
3
)
g
4
= f
5
− f
8
= − Y
2
+ Y
3
− c(X
2
− X
3
+ (x
2
− x
3
)σ
1
) + (y
2
− y
3
)σ
2
+ a(Z
2
− Z
3
+ (z
2
− z
3
)σ
3
)
g
5
= f
3
− f
9
= − Z
1
+ Z
3
+ b(X
1
− X
3
+ (x
1
− x
3
)σ
1
) − a(Y
1
− Y
3
+ (y
1
− y
3
)σ
2
) + (z
1
− z
3
)σ
3
g
6
= f
6
− f
9
= − Z
2
− Z
3
+ b(X
2
− X
3
+ (x
2
− x
3
)σ
1
) − a(Y
2
− Y
3
+ (y
2
− y
3
)σ
2
) + (z
2
− z
3
)σ
3
.
(17.33)
In the remaining 6 equations (g
i
= 0) there are only 6 unknown parameters (a,
b, c, σ
1
, σ
2
, σ
3
). This system can be simplified by the introduction of the relative
coordinates as was the case for the 7-parameter transformation.
x
ij
= x
i
− x
j
, y
ij
= y
i
− y
j
, z
ij
= z
i
− z
j
X
ij
= X
i
− X
j
, Y
ij
= Y
i
− Y
j
, Z
ij
= Z
i
− Z
j
.
→ i, j ∈ {1, 2, 3}, i 6= j (17.34)
Then our equation system becomes
g
1
= −X
13
+ cY
13
− bZ
13
+ x
13
σ
1
+ cy
13
σ
2
− bz
13
σ
3
g
2
= −X
23
+ cY
23
− bZ
23
+ x
23
σ
1
+ cy
23
σ
2
− bz
23
σ
3
g
3
= −cX
13
− Y
13
+ aZ
13
− cx
13
σ
1
+ y
13
σ
2
+ az
13
σ
3
g
4
= −cX
23
− Y
23
+ aZ
23
− cx
23
σ
1
+ y
23
σ
2
+ az
23
σ
3
g
5
= +bX
13
− aY
13
− Z
13
+ bx
13
σ
1
− ay
13
σ
2
+ z
13
σ
3
g
6
= +bX
23
− aY
23
− Z
23
+ bx
23
σ
1
− ay
23
σ
2
+ z
23
σ
3
.
(17.35)
17-412 Symbolic solution with Dixon resultant
Symbolic solution of the s ystem g
i
means the reduction of the multivariate polyno-
mial system via computer algebra to a single univariate polynomial and computing
its roots. Then the other unknowns can be computed backwards, as done in the
Gauss elimination method for solving linear systems of equations. In the case of
the affine transformation, the system can be reduced with different methods to a
univariate polynomial containing only one scale parameter σ
i
. This can be done by
Dixon resultant with Kapur-Saxena-Yang and with the Early Discovery Factors
322 17 Datum transformation problems
(EDF) method also, see Pal´ancz et al. [325] and Zaletnyik and Pal´ancz [431]. Em-
ploying the Kapur-Saxena-Yang method, using pairwise-elimination step by step,
a univariate polynomial of degree 29 for σ
1
is obtained, see. e.g., [430, 432]. To find
the proper solution of this polynomial of degree 29, a good initial value is needed.
The univariate polynomial for σ
1
can also be computed by employing the ac-
celerated Dixon resultant by the EDF algorithm, which was suggested and imple-
mented in the computer algebra system Fermat by Lewis [267, 269]. Using this
method one can get the results in the following form
5
Y
i=1
ϕ
i
(σ
1
)
K
i
(17.36)
where ϕ
i
(σ
1
) are irreducible polynomials with low degrees, but their powers, K
i
are very large positive integer numbers. Expanding this expression would result in
millions of terms. Consequently, we shall consider K
i
= 1, for i = 1, . . . , 5, namely
5
Y
i=1
ϕ
i
(σ
1
) (17.37)
as the Dixon resultant. These polynomials are as follows
ϕ
1
=y
13
z
23
− y
23
z
13
;
ϕ
2
=x
2
13
y
23
z
23
σ
2
1
− x
13
x
23
y
13
z
23
σ
2
1
− x
13
x
23
y
23
z
13
σ
2
1
+ x
2
23
y
13
z
13
σ
2
1
− Z
2
13
y
23
z
23
− Y
2
13
y
23
z
23
− X
2
13
y
23
z
23
+ Z
13
Z
23
y
13
z
23
+ Y
13
Y
23
y
13
z
23
+ X
13
X
23
y
13
z
23
+ Z
13
Z
23
y
23
z
13
+ Y
13
Y
23
y
23
z
13
+ X
13
X
23
y
23
z
13
− Z
2
23
y
13
z
13
− Y
2
23
y
13
z
13
− X
2
23
y
13
z
13
;
ϕ
3
=x
13
y
23
σ
1
− x
23
y
13
σ
1
+ X
13
y
23
− X
23
y
13
;
ϕ
4
=Z
13
x
13
x
23
z
23
σ
2
1
− Z
23
x
2
13
z
23
σ
2
1
− Z
13
x
2
23
z
13
σ
2
1
+ Z
23
x
13
x
23
z
13
σ
2
1
+ X
13
Z
13
x
23
z
23
σ
1
− 2 X
13
Z
23
x
13
z
23
σ
1
+ X
23
Z
13
x
13
z
23
σ
1
+ X
13
Z
23
x
23
z
13
σ
1
− 2 X
23
Z
13
x
23
z
13
σ
1
+ X
23
Z
23
x
13
z
13
σ
1
− X
2
13
Z
23
z
23
+ X
13
X
23
Z
13
z
23
+ X
13
X
23
Z
23
z
13
− X
2
23
Z
13
z
13
;
ϕ
5
=Z
13
z
23
− Z
23
z
13
;
(17.38)
From these factor polynomials, one which provides the good (positive and real)
solution is selected. In the case of more than one real, positive solution, an initial
value can help in deciding the correct polynomial.
Fortunately for the value of σ
1
, a very good estimation can be given as σ
1
=
1 /s
1
, where s
1
(the first scale parameter) can be estimated by dividing the sum
of distances from the center of gravity in both systems, see e.g., Albertz and
Kreiling [8].
The factor polynomial providing the proper root (ϕ
4
), has degree 2, therefore
its solution can be expressed in an analytical form (only one of the roots is correct,
the positive σ
1
). Similarly, we can also get simple explicit forms for σ
2
and σ
3
.

17-4 Algebraic solution of the 9-parameter transformation 323
The results of the Dixon-EDF method is not only faster and more elegant, but
also more precise than that of the Dixon-KSY method. However, one should still
check the solutions of all polynomials with degrees 1 and 2 in order to choose the
prop e r results.
17-413 Symbolic solution with reduced Groebner basis
The same results for σ
i
, i = 1, 2, 3 can be achieved by using the reduced Groebner
basis built in to Mathematica, where the monomial order should be defined as the
elimination order (Lichtblau
3
, Private Communication). With Groebner basis, the
solutions of σ
1
, σ
2
and σ
3
as a second order univariate polynomial can be obtained
in one step.
For σ
1
for instance, one writes in Mathematica:
σ
1
=GroebnerBasis[{g
1
, g
2
, g
3
, g
4
, g
5
, g
6
}, σ
1
, {a, b, c, σ
2
, σ
3
},
MonomialOrder → EliminationOrder]
Solving the problem with Groebner basis has the advantage that the solution for
σ
i
can be obtained in one step without the need to select the proper solution using
good initial values. For all σ
i
, the resulting univariate polynomials are of degree
2 where only one solution is positive. Its solution can therefore be expressed in
analytical form as expressed by equations (17.39)-(17.41), i.e.,
σ
1
=
X
2
23
y
13
z
13
+ y
13
Y
2
23
z
13
+ X
2
13
y
23
z
23
+ Y
2
13
y
23
z
23
+ y
23
Z
2
13
z
23
− X
13
X
23
(y
23
z
13
+ y
13
z
23
) − Y
13
Y
23
(y
23
z
13
+ y
13
z
23
) − y
23
z
13
Z
13
Z
23
−
y
13
Z
13
z
23
Z
23
+ y
13
z
13
Z
2
23
1/2
/ [(x
23
y
13
− x
13
y
23
)(x
23
z
13
− x
13
z
23
)]
1/2
(17.39)
σ
2
=
−X
2
13
x
23
z
23
+ X
13
X
23
(x
23
z
13
+ x
13
z
23
)
+ x
23
Y
13
Y
23
z
13
− Y
2
13
z
23
− Z
2
13
z
23
+ z
13
Z
13
Z
23
− x
13
X
2
23
z
13
+ Y
2
23
z
13
− Y
13
Y
23
z
23
− Z
13
z
23
Z
23
+ z
13
Z
2
23
1/2
/ [(x
13
y
23
− x
23
y
13
)(y
13
z
23
− y
23
z
13
)]
1/2
(17.40)
and
σ
3
=
X
2
13
x
23
y
23
− X
13
X
23
(x
23
y
13
+ x
13
y
23
)
+ x
23
Y
2
13
y
23
− y
13
Y
13
Y
23
+ y
23
Z
2
13
− y
13
Z
13
Z
23
+ x
13
X
2
23
y
13
− Y
13
y
23
Y
23
+ y
13
Y
2
23
− y
23
Z
13
Z
23
+ y
13
Z
2
23
1/2
/ [(x
23
z
13
− x
13
z
23
)(y
23
z
13
− y
13
z
23
)]
1/2
(17.41)
3
researcher of Wolfram Research
