Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

324 17 Datum transformation problems

Knowing σ

, σ

the equation system g

(Eq.(17.35)) will be linear and a, b, c

can be expressed easily analytically by

a = − [−X

+ X

+ (X

− X

)σ

+ σ

(−x

+ x

+ (x

− x

)σ

)]/

− X

+ (X

− X

)σ

+ σ

− x

+ (x

− x

)σ

)]

, (17.42)

b = − [−Y

+ Y

+ (Y

− Y

)σ

+ σ

(−y

+ y

+ (y

− y

)σ

)]/

[−X

+ X

+ (−X

+ X

)σ

+ σ

(−x

+ x

+ (−x

+ x

)σ

)]

, (17.43)

and

c = − [X

− X

+ (X

− X

)σ

+ σ

(−x

+ x

+ (−x

+ x

)σ

)]/

[−Y

+ Y

+ (−Y

+ Y

)σ

+ σ

(−y

+ y

+ (−y

+ y

)σ

)]

. (17.44)

Substituting (a, b, c, σ

, σ

) in to the original equation (Eq. (17.24)), the

translation parameters (X

, Y

, Z

) can be calculated using

















− WR

















− Ω

−1

















−





1/σ

0 0

0 1/σ

0 0 1/σ





1 + a

+ b

+ c





1 + a

− b

− c

2(ab −c) 2(b + ac)

2(ab + c) 1 − a

+ b

− c

2(−a + bc)

2(−b + ac) 2(a + bc) 1 − a

− b

+ c













(17.45)

As we have seen in this section, the Dixon-KSY method as well as the Dixon-EDF

method required the estimation of the initial values to select the proper solution

from diﬀerent solutions. With reduced Groebner basis, we get the same solution

in one step as the proper solution of the Dixon-EDF method. With this metho d,

a fully analytic solution requiring neither initial conditions nor iterations can be

given.

The computer algebra method, namely the accelerated Dixon resultant with

the technique of Early Discovery Factors as well as the reduced Groebner basis,

provides a very simple, elegant symbolic solution for the 3-points problem. The

main advantages of the symbolic solutions originate from its iteration-free feature,

very short- practically zero-computation time, and the independence of the value

of the actual numerical data.

17-4 Algebraic solution of the 9-parameter transformation 325

The symbolic solution of the 3-points problem can be used for the N-points

problem also. One possibility is to use the solutions of the 3-points problem as

initial guess value for solving the N -points problem with some local numerical

method. Another possibility is just to use the solutions of the diﬀerent triplets in

the Gauss-Jacobi combinatorial method.

17-42 The N-points problem

For local numerical methods the initial values can be computed from the 3-points

model, but one nee d to be cautious and not to compute it blindly. In this section,

we shall discuss how one can properly select 3-points from the N ones, in order to

compute good initial values ensuring fast convergence of the Newton-type methods

employed for the solution of the N-points problem.

We will examine a numerical example with 81 ﬁrst order Hungarian stations,

with coordinates in both the global system of ETRS89 and the local Hungarian

system HD72 (Hungarian Datum 1972). Let us choose two diﬀerent sets each

containing 3 points from the local datum data set (see Fig. 17.4) and calculate

using symbolic solution the parameters of the coordinate transformation between

the global WGS84 and the local Hungarian system. The results for the two triplets

100000

200000

300000

400000

400000 500000 600000 700000 800000 900000

Control points

Triplet leading to

a bad geometry

Triplet leading to

a good geometry

Figure 17.4. Map of Hungary showing the 81 points in the local coordinate system

together with the chosen triplets

are quite diﬀerent, as shown in Table 17.11.

Using the parameters of the 1st set of Table (17.11) as initial values for the

Newton-Raphson method to solve the N -p oints problem (here, all the N=81 points

326 17 Datum transformation problems

Table 17.11. Calculated coordinate transformation parameters from two diﬀerent sets

for the case of Hungarian Datum (81 points) to ETRS89 coordinate system

set 2

set

-77.523 -496.192

+90.366 +124.797

+25.151 +543.061

a +1.520 · 10

−6

+5.470 ·10

−6

b +1.526 · 10

−6

+27.692 ·10

−6

c −0.543 · 10

−6

−2.415 ·10

−6

0.999998865 0.999957317

1.000001182 0.999989413

1.000001642 1.000069623

of Hungary), the method converges rapidly after 4 iteration steps. On replacing the

values of the 1st set with those of the 2nd set, the method does not converge even

after 100 iteration steps (see Pal´ancz et al. [325]). This signiﬁes the importance

of properly selecting the 3 points from the N-points to calculate symbolically the

initial guess values for the N-points problem.

There exists a correlation between the geometry of the chosen triplet and the

goodness of the calculated initial values. According to our numerical example, we

get the best initial values when the geometry of the triplet is similar to an equilateral

triangle, and the worst case when the geometry of the three points is nearly on

a line. A geometrical index can be introduced to represent the geometry of the

selected 3 points to avoid the solutions which provide disadvantageous starting

values. This geometrical index is the sine of the minimum angle in the triangle, it’s

maximal value is

√

when the triangle is an equilateral triangle, and around zero

when the three points are nearly collinear . In the earlier examples, the geometrical

index in the ﬁrst case (Fig. 17.4, good geometry), which gave good initial values,

was 0.529 and in the s ec ond case (Fig. 17.4, bad geometry) was 0.002.

To check the correlation between the geometry and the goodness of the initial

values, we calculated the transformation parameters for all 3-point combinations

from the 81 points, giving a total of 85320 combinations. We then examined all

the resulting Z

values for combinations. The real Z

value calculated using the

Newton-Raphson method from the 81 points was 50.342 m, but the values calcu-

lated from the diﬀerent triplets can be very diﬀerent from this, for example the

maximum value for Z

was 24 679 629 m! The geometrical index of this extreme

triplet was 0.003, me aning that these 3 points were almost collinear.

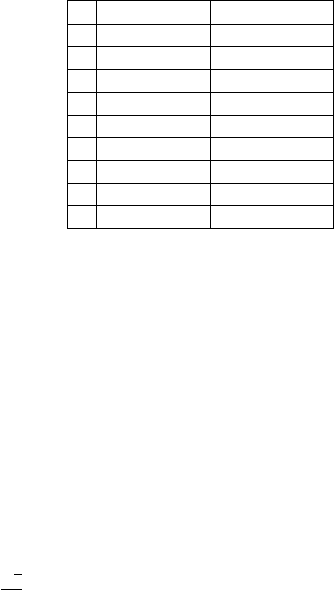
In Figure 17.5, the calculated Z

values are presented as a function of the

geometrical index for all 85320 combinations (for a better representation, |Z

| >

1000 values are not represented since they are too large, e.g., the minimum Z

-1 798 501 and the maximum is 24 679 629). The true value of Z

based on the 81

data points is also represented by a line.

17-4 Algebraic solution of the 9-parameter transformation 327

Figure 17.5. Values of Z

as function of the geometrical index for all combinations of

triplets from the 81 point Hungarian data set (see Fig. 17.4)

The triplets that give extremely diﬀerent solutions from the adjusted value all

have geometrical indices less then 0.1. In this range, the round-oﬀ error is domi-

nating. For higher values of this index, the improper ﬁtting of the measurement

data to the 9 parameter model causes the deviations in value of Z

. In general, the

more similar the geometry of the selected three points is to an equilateral triangle,

the better is the initial value for of the N-points problem. It is therefore shown

by this example that it is very important to examine the geometry of the selec ted

three points for calculating the initial values, and to avoid nearly collinear triplets

(see Zaletnyik [430]).

17-421 ALESS approach to overdetermined cases

In the cases where more than 3-points with known c oordinates in both coordinate

systems are known, as is usually the case, there are more independent equations

than unknown variables leading to an overdetermined system. These equations

generally are inconsistent due to inevitable stochastic observation and model er-

rors. In such a situation, the 3 nonlinear equations can be written for a single point

(according to Eq. (17.31) as:

= −X

+ cY

− bZ

+ x

− X

+ cy

− cY

− bz

+ bZ

= −cX

− Y

+ aZ

− cx

+ cX

+ y

− Y

+ az

− aZ

=bX

− aY

− Z

+ bx

− bX

− ay

+ aY

+ z

− Z

(17.46)

where vx

, vy

and vz

are 0 when we have the minimally required 3 homologous

points to determine the 9 unknown parameters. However, when we have to solve

an overdetermined system, vx

, vy

and vz

are not zero, because of the inevitable

observation and model errors.

For N > 3 homologous points, the nonlinear system to be solved leads to a sys-

tem of 3N polynomial equations, minimizing

where v

= (vx

+ vy

+ vz

In our numerical example, we will use 1138 points from the Hungarian OGPSH

database, with coordinates in the global system of ETRS89 and in the local Hun-

garian system HD72 (Hungarian Datum 1972) (using the ellipsoidal coordinates

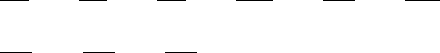
328 17 Datum transformation problems

without height parameter). For example, we have N = 1138 points which means

we have 3414 equations and 9 unknown parameters, leading to an overdetermined

multivariate polynomial system.

This overdetermined model can b e transformed into a determined one by em-

ploying symbolic evaluation of the objective function (∆ =

i=1

), and its

symbolic derivation, providing the necessary condition of its minimum (see Sect.

7-2). The objective function

∆(a, b, c, X

, Y

, Z

, σ

) =

i=1

(vx

+ vy

+ vz

). (17.47)

can be created easily with Computer Algebra Systems as

∆ =



+ b

+ c

− 2abX

+ Y

+ a

+ c

− 2acX

−

2bcY

+ Z

+ a

+ b

− 2x

+ 2b

+ 2c

− 2b

− 2c

− 2abx

+ 4cx

2abX

− 4cX

− 4bx

− 2acx

+ 4bX

2acX

+ x

+ b

+ c

− 2x

− 2b

−

+ X

+ b

+ c

− 2abX

−

4cX

+ 2abX

+ 4cX

− 2y

+ 2a

+ 2Y

− 2a

− 2c

+ 4ay

−

2bcy

− 4aY

+ 2bcY

− 2abx

2abX

+ 2abx

− 2abX

+ y

+ c

− 2y

− 2a

− 2c

+ a

+ c

+ 4bX

− 2acX

− 4aY

−

2bcY

− 4bX

+ 2acX

+ 4aY

+ 2bcY

−

+ 2a

+ 2b

+ 2Z

− 2a

−

− 2acx

+ 2acX

+ 2acx

−

2acX

− 2bcy

+ 2bcY

+ 2bcy

−

2bcY

+ z

+ a

+ b

− 2z

−

− 2b

+ Z

+ a

+ b



. (17.48)

The necessary conditions of the minimum for the objective function are

∂∆

∂a

= 0,

∂∆

∂b

= 0,

∂∆

∂c

= 0,

∂∆

∂X

= 0,

∂∆

∂Y

= 0,

∂∆

∂Z

= 0,

∂∆

∂σ

= 0,

∂∆

∂σ

= 0,

∂∆

∂σ

= 0.

(17.49)

Considering the necessary conditions for the minimum, we have 9 equations and

9 variables. However, in this case the determined system are of a higher order and

more complex polynomial system than the original overdetermined one, leading

to most of these equations having many thousands of terms. It is therefore useful

to collect terms corresponding to the same multivariate expression via computer

algebra, see Zaletnyik [430]. Here, just as an illustration, let us see the ﬁrst equation

17-4 Algebraic solution of the 9-parameter transformation 329

resulting from the derivation of the objective function with respect to the variable

a (the whole system (F

, F

, . . . , F

) can be found in Appendix A-4),

(a, b, c, σ

, σ

, X

, Y

, Z

) =

∂∆

∂a

− bNX

+ aNY

− cNX

+ aNZ

+ bY

i=1

+ cZ

i=1

+ bY

i=1

+ cZ

i=1

+ aY

i=1

(−2y

)

+ bX

i=1

+ bσ

i=1

(−x

) + bσ

i=1

(−X

) + aσ

i=1

+ aY

i=1

(−2Y

) + bX

i=1

+ Z

i=1

+ bσ

i=1

(−x

)

+ b

i=1

(−X

) + aσ

i=1

+ aZ

i=1

(−2z

) + cX

i=1

+ cσ

i=1

(−x

) + cσ

i=1

(−X

) + σ

i=1

(−2Y

) + aσ

i=1

+ Y

i=1

(−2Z

) + aZ

i=1

(−2Z

) + cX

i=1

+ cσ

i=1

(−x

)

+ c

i=1

(−X

) + σ

i=1

+ aσ

i=1

+ a

i=1



+ Z



= 0.

(17.50)

In this way we get 9 polynomial equations (see also [323, 430]) with the 9 unknown

parameters (a, b, c, X

, Y

, Z

, σ

17-422 Homotopy solution of the ALESS-determined model

Diﬀerent possibilities exist for solving the determined system created using ALESS

method. One c an use global methods to ﬁnd all of the solutions of the determined

system, and then select only the good solution which provides the least value of

the objective function of ALESS. Another approach is to use local methods, like

the extended Newton-Raphson method or Newton type homotopy, in the case of

good initial values (see Chap. 6).

To solve such a complicated system as the 9-equation system created by ALESS

in symbolic form is a diﬃcult problem which, until now, has had no solution.

The global homotopy solution, calculating automatically the start systems is also

problematic. The highest order term in every equation is 5, therefore the degree

of every equation is d

= 5, i = 1, . . . , 9. This implies that the upper bound of

the number of the solutions of this system is 5

= 1953125, which means that

to use the homotopy solution with the automatically calculated start sys tem for

polynomial systems, we would need to track nearly 2 millions paths

Remark: Tracking millions of paths is not unrealistic on supercomputers, clusters

of workstations or even modern multiprocessor, multi-core desktop computers, see Blum

et al. [84].

330 17 Datum transformation problems

We have seen in Sect. 6-42, that one of the most simple ways to deﬁne a

start system is by employing Newton-type homotopy, see Eq. (6.26). This type of

homotopy requires a guess value for the solution of the original (target) system.

Now seemingly, we have arrived back to our original problem of the m issing proper

initial value for local methods like Newton-Raphson. However, the situation is not

so bad. On the one hand, we do not need a proper initial value, because homotopy

is much more robust than local methods, and enlarges the domain of convergence.

On the other hand, there are natural ways to compute the initial value, which is

good enough for homotopy.

One possibility is to use the result of the symbolic solution of the 3-point

problem. As we have seen in the previous sec tion, the values calculated from the

diﬀerent triplets can diﬀer signiﬁcantly, depending on their geometrical conﬁgura-

tions. A solution for one of the geometrically ill-posed triplets is illustrated in Table

17.12. In this Table, we represent the calculated parameters in their traditional

geodetic forms, i.e., representing the rotation matrix with the three rotation angles

(α, β, γ) in seconds, instead of a, b, c, and the deviations of the scale parameters

from one (k

= s

−1 = 1/σ

−1), in ppm (part per million)), instead of the inverse

scale parameters (σ

, σ

Table 17.12. The start values computed from a symbolical 3-points solution

Variables Start values in geodetic form

˜a −0.00002 ˜α = +8.2508”

b 0.00002

β = −8.2504”

˜c 0.00002 ˜γ = −8.2508”

−243

= −243 m

−227

= −227 m

337

= +337 m

˜σ

= 0 ppm

˜σ

= 0 ppm

˜σ

= 0 ppm

Another way to calculate a guess value is to delete the nonlinear terms from

the original overdetermined system, e.g., from Eqs. (17.46).

Lvx

= −X

+ cY

− bZ

+ x

Lvy

= −cX

− Y

+ aZ

+ y

Lvz

= bX

− aY

− Z

+ z

(17.51)

The least square solution of this linear system i = 1, . . . , 1138 can be computed via

pseudoinverse with 1138 Hungarian data points. The result is presented in Table

17.13 which indicates that the two diﬀerent methods gave fairly diﬀerent values

and both are far from the des ired solution, see e.g., Table 17.14.

Employing Newton homotopy, the start system is,

17-4 Algebraic solution of the 9-parameter transformation 331

Table 17.13. The start values computed from Eqs.(17.51) via pseudoinverse

Variables Start values in geodetic form

˜a −5.14934436480436 ·10

−6

˜α = +2.1244”

b 9.147743927965785 · 10

−6

β = −3.7736”

˜c 0.0000472128892111371 ˜γ = −19.4767”

3.78794980367417 ·10

−17

= 0.000 m

˜σ

1.0000011141420198

= −1.114 ppm

˜σ

1.0001180993441208

= −118.085 ppm

˜σ

0.9999810252524541

= +18.975 ppm

G(χ) = F (χ) − F (χ

) (17.52)

with F = (F

(χ), F

(χ)) as

the target system, χ = (a, b, c, X

, Y

, Z

, σ

) as the unknown variables and

= (˜a,

b, ˜c,

, ˜σ

) as the start (initial) values for the homotopy

function. The homotopy function is then given by (see, e.g., Eq. (6.28).

H(χ, λ) = F (χ) − (1 − λ)F (χ

) . (17.53)

The solution for all parameters are presented in Table 17.14. The Newton homo-

topy solution was successful with both initial values. As an illustration, Fig. 17.6

shows the paths of the homotopy solution in the complex plain for the parameter

a using the two diﬀerent initial values.

Table 17.14. Homotopy solution for the 1138 Hungarian points

Variables Homotopy solutions in geodetic form

a −8.389143102087336 ·10

−6

α = +3.4591”

b 0.00011415902600771965 β = −47.094”

c -0.00003482245241765358 γ = +14.3649”

-2298.5887892237693 X

= −2298.589 m

526.5088259777841 Y

= +526.509 m

2143.7159886648537 Z

= +2143.716 m

0.9997302444546577 k

= +269.828 ppm

1.000188709705781 k

= −188.674 ppm

1.000245242648286 k

= −245.183 ppm

Table 17.15 shows the results of the diﬀerent methods in case of the diﬀerent

initial guess values. It can be seen that the traditional Newton-Raphson method

failed in both cases, while its modiﬁcation, the Newton-Krylov method, had a singu-

larity in the ﬁrst case, and was slowed down by the increasing number of iterations

332 17 Datum transformation problems

Figure 17.6. Paths of the homotopy solution in the complex plain for the parameter a,

with two diﬀerent initial values

required to ensure acceptable precision in the second case. In this example, ho-

motopy solution seemed to be more robust as well as faster than the traditional

Newton’s type methods. Fig. 17.6 demonstrates clearly how large the domain of

convergency of the homotopy method is.

Table 17.15. Comparing diﬀerent methods for the case of 1138 Hungarian points for

3D aﬃne transformation

Computation time [s]

Metho d with initial values in

Table 17.12 Table 17.13

Newton-Raphson fails to converge converging to a wrong solution

Newton-Krylov singularity 3.5

Newton-Homotopy 0.72 0.73

17-4 Algebraic solution of the 9-parameter transformation 333

17-43 Procrustes solution

Example 17.3 (Computation of 7-parameter transformation incorporating weights).

We consider Cartesian coordinates of seven stations given in the local and global

system (WGS-84) as in Tables 17.1 and 17.2 on pp. 309. Desired are the 7-datum

transformation parameters; scale x

, the translation vector x

∈ R

3×1

and the

rotation matrix R ∈ R

3×3

. In addition to these 7 datum transformation param-

eters, we compute for control purposes the residual (error matrix) E upon which

the mean error norm (9.55) is determined as a scalar measure of error of types

W-LESS. A two step procedure is carried out as follows:

In the ﬁrst step, we computed the 7 transformation parameters using I-LESS

(with weight matrix as identity) from Corollary 9.4 on p. 127. The computed

values of scale x

and the rotation matrix R ∈ R

3×3

are used in (9.94) to obtain

the dispersion of the error matrix E. In-order to obtain the dispersions Σ

v ecY

∗

and

v ecY

∗

of the pseudo-observations in the local and global systems respectively, we

make use of “p ositional error sphere” for each point (position) in both systems.

Here, the positional error sphere refers to the average of the variances (σ

(σ

+ σ

)/3) for the i = 7 points involved so as to achieve the isotropic

condition.

The identity matrices are multiplied by these positional error spheres so as to

obtain the dispersion matrices Σ

v ecY

∗

and Σ

v ecY

∗

which fulﬁll the isotropic con-

dition. One obtains therefore the dispersion matrices Σ

v ecY

∗

and Σ

v ecY

∗

as being

diagonal block matrices with each blo ck corresponding to the variance-covariance

matrices of the respective position. For points 1 and 2 in the local system for

instance, assuming no correlation between the two p oints, one obtains

vecY

∗













, (17.54)

where {σ

, σ

} are pos itional error spheres for points 1 and 2, respectively. This

is also performed for Σ

v ecY

∗

and the resulting dispersion matrices used in (9.94)

to obtain the dispersion matrix of the error matrix E.

Since the obtained block diagonal error matrix E is a 3n × 3n matrix, the

n × n matrix is extracted by taking the trace of the block diagonal matrices of E.

Adopting such a matrix from [169, Table 7] as

W =







1.8110817 0 0 0 0 0 0

0 2.1843373 0 0 0 0 0

0 0 2.1145291 0 0 0 0

0 0 0 1.9918578 0 0 0

0 0 0 0 2.6288452 0 0

0 0 0 0 0 2.1642460 0

0 0 0 0 0 0 2.359370







(17.55)