Astakhov V. Tribology of Metal Cutting

Подождите немного. Документ загружается.

Design of Experiments in Metal Cutting Tests 307

Table 5.13. Experimental results for cutting force components.

Cutting edge number Statistical relationships for the cutting force components

(N) F

(N)

1 1497t

0.98

0.81

450t

0.81

594t

0.94

0.61

2 1560t

0.98

0.78

585t

1.07

0.96

636t

0.93

0.66

3 1620t

0.94

0.77

770t

0.92

0.90

728t

0.93

0.63

The same approach was used to obtain the equations for the cutting force compo-

nents (Table 5.13) acting on each part of the drill (3 cutting edges having width

and d

5.5 Group Method of Data Handling

5.5.1 Background

Group Method of Data Handling (GMDH) was applied in a great variety of areas for

data mining and knowledge discovery, forecasting and systems modeling, optimiza-

tion and pattern recognition [20–23]. Inductive GMDH algorithms provide a possibility

to ﬁnd interrelations in data automatically, to select the optimal structure of model

or network and to increase the accuracy of existing algorithms. This original self-

organizing approach is substantially different from deductive methods commonly used

for modeling. It has inductive nature – it ﬁnds the best solution by sorting-out pos-

sible alternatives and variants. By sorting different solutions, the inductive modeling

approach aims to minimize the inﬂuence of the experimentalist on the results of model-

ing. An algorithm itself can ﬁnd the structure of the model and the laws, which act in

the system. It can be used as an advisor to ﬁnd new solutions of artiﬁcial intelligence

(AI) problems.

GMDH is a set of several algorithms for different problems solution. It consists of para-

metric, clusterization, analogs complexing, rebinarization and probability algorithms.

This self-organizing approach is based on the sorting-out of models of different levels of

complicity and selection of the best solution by a minimum of external criterion character-

istic. Not only polynomials but also non-linear, probabilistic functions or clusterizations

are used as basic models.

In the author’s opinion, the GMDH approach is the most suitable for metal cutting studies

because:

• The optimal complexity of model structure is found, adequate to the level of noise

in the data sample. For real problems solution with noisy or short data, simpliﬁed

forecasting models are more accurate.

• The number of layers and neurons in hidden layers, model structure and other

optimal neutral network (NN) parameters are determined automatically.

308 Tribology of Metal Cutting

• It guarantees that the most accurate or unbiased models will be found – method

does not miss the best solution during the sorting of all variants (in a given class of

functions).

• Any non-linear functions or features can be used as input variables, which can

inﬂuence the output variable.

• It automatically ﬁnds interpretable relationships in data and selects effective input

variables.

• GMDH sorting algorithms are rather simple for programming.

• The method uses information directly from the data samples and minimizes the

inﬂuence of a priori researcher assumptions about the results of modeling.

• GMDH neuronets are used to increase the accuracy of other modeling algorithms.

• The method allows ﬁnding an unbiased physical model of object (law or

clusterization) – one and the same for all future samples.

There are many published articles and books devoted to GMDH theory and its applica-

tions. The GMDH can be considered as a further propagation or extension of inductive

self-organizing methods to the solution of more complex practical problems. It solves

the problem of how to handle the data samples of observations. The goal is to obtain

a mathematical model of the object under study (the problem of identiﬁcation and pat-

tern recognition) or to describe the processes, which will take place at the object in the

future (the problem of process forecasting). GMDH solves, by means of a sorting-out

procedure, the multidimensional problem of model optimization

g =argmin

g⊂G

(

)

(

)



P, S,z



, (5.48)

where G is a set of models considered, CR is the external criterion of the model g quality

from this set, P is the number of variables set, S is model complexity, z

is the noise

dispersion, T

is the number of data sample transformation and V is the type of reference

function.

For the deﬁnite reference function, each set of variables corresponds to deﬁnite model

structure P =S. Problem transforms to much simpler one-dimensional

(

)

(

)

(5.49)

when z

= constant, T = constant and V = constant

The method is based on the sorting-out procedure, i.e. consequent testing of models,

chosen from a set of model candidates in accordance with the given criterion. Most

of the GMDH algorithms use the polynomial reference functions. General correlation

between the input and output variables can be expressed by Volterra functional series,

discrete analog of which is Kolmogorov–Gabor polynomial

y =b

i=1

j=1

i=1

j=1

k=1

ijk

, (5.50)

Design of Experiments in Metal Cutting Tests 309

where X(x

, x

,...,x

) is the input variables vector, M is the number of input variables

and A(b

, b

, ..., b

) is the vector of coefﬁcients.

Components of the input vector X can be independent variables and functional forms or

ﬁnite difference terms. Other non-linear reference functions, such as difference, proba-

bilistic, harmonic and logistic can also be used. The method allows ﬁnding simultaneously

the structure of model and the dependence of modeled system output on the values of

most signiﬁcant inputs of the system.

GMDH, based on the self-organizing principle, requires minimum information about

the object under study. As such, all the available information about this object should

be used. The algorithm allows ﬁnding the needed additional information through the

sequential analysis of different models using the so-called external criteria. Therefore,

GMDH is a combined method: it uses the test data and sequential analysis and estimation

of the candidate models. The estimates are found using relatively small part of the test

results. The other part of these results is used to estimate the model coefﬁcients and to

ﬁnd the optimal model structure.

Although GMDH and regression analysis use the table of test data, the regression analysis

requires the prior formulation of the regression model and its complexity. This is because

the row variances used in the calculations (Section, Statistical Examination of the Result

Obtained, Eq. (5.26)) are internal criteria. A criterion is called an internal criterion if its

determination is based on the same data that is used to develop the model. The use of any

internal criterion leads to a false rule: the more complex model is more accurate. This

is because the complexity of the model is determined by the number and highest power

of its terms. As such, the greater the number of terms, the smaller the variance. GMDH

uses the external criteria. A criterion is called external if its determination is based on

new information obtained using “fresh” points of the experimental table not used in

the model development. This allows the selection of the model of optimum complexity

corresponding to the minimum of the selected external criterion.

Another signiﬁcant difference between the regression analysis and GMDH is that the

former allows construction of the model only in the domain where the number of model

coefﬁcients is less than the number of points of the design matrix because the examination

of model adequacy is possible only when f

> 0, i.e. when the number of estimated

coefﬁcients of the model (n) is less than the number of points in the design matrix (m).

GMDH allows much wider domain where, for example, the number of model coefﬁcients

can be millions and all these are estimated using the design matrix containing only 20

rows. In this new domain, accurate and unbiased models are obtained. GMDH algorithms

utilize minimum experimental information on input. This input consists of a table having

10–20 points and the criterion of model selection. The algorithms determine the unique

model of optimal complexity by the sorting out of different models using the selected

criterion.

The essence of the self-organizing principle in GMDH is that the external criteria pass

their minimum when the complexity of the model is gradually increased. When a par-

ticular criterion is selected, the computer executing GMDH ﬁnds this minimum and the

corresponding model of optimal complexity. As such, the value of the selected criterion

referred to as the depth of minimum can be considered as an estimate of the accuracy

310 Tribology of Metal Cutting

and reliability of this model. If sufﬁciently deep minimum is not reached then the model

is not found. This might take place when the input data (the experimental data from the

design matrix) are: (1) noisy; (2) do not contain essential variables; (3) the basic function

(for example, polynomial) is not suitable for the process under consideration, etc.

5.5.2 Example: tool life testing

Design matrix. As the metal cutting process takes place in the cutting system, it depends

on many system parameters whose complex interactions make it difﬁcult to describe

the system mathematically. Due to complexity of the factors’ interaction, the cutting

process can be compared with “natural” processes which are known as “poorly orga-

nized.” This is because it is very difﬁcult to establish the cause–effect links between

the input and output variables of the real cutting process through direct observations

of this process. That is why so many explanations for the same machining phenom-

ena (for example, the shear bands in the chip) and theories of the cutting process exist

today.

The preliminary tests have shown that the cutting regime (the cutting speed (v) and

feed (f )) and the parameters of the tool geometry should be considered as the input

variables. Tool life is to be considered as the output parameter. Therefore, the prob-

lem is to correlate the input variables with the output parameter using a statistical

model. In other words, it is necessary to ﬁnd a certain function (whether linear

or not)

A =F





(5.51)

which is continuous with respect to the vector of arguments ¯x =

(

¯x

, ¯x

,...,¯x

)

each

of which can be varied independently in the range

[

¯x

min

, ¯x

max

]

. In Eq. (5.52),

B =



,...,



is the vector of the estimates for the model’s coefﬁcients.

The vector of input variables contains 11 variables (M =11) which are (Fig. 5.8):

is the approach angle of the outer cutting edge (ϕ

is the approach angle of the inner cutting edge (ϕ

is the normal ﬂank angle of the outer cutting edge (α

is the distance c

shown in Fig. 5.8,

is the distance c

shown in Fig. 5.8,

is the location distance of the drill point with respect to the x axis of the tool coordinate

system (m

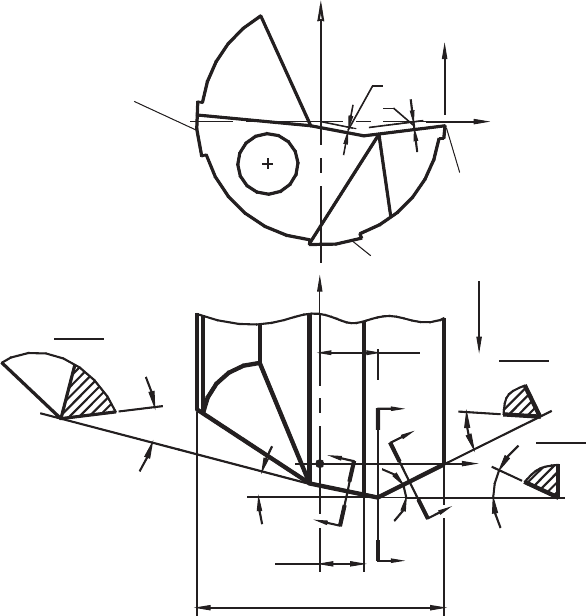
Design of Experiments in Metal Cutting Tests 311

A−A

B−B

C−C

Ø35.00

Trailing pad

Leading pad

Drill corner

f(mm/rev)

n(m/min)

Fig. 5.8. Variables included in the test.

is the location distance of the two parts of the tool rake face with respect to the x axis

of the tool coordinate system (m

is the ﬂank angle of the auxiliary ﬂank surface (α

is the cutting speed (v) (m/min),

is the cutting feed (f ) (mm/rev).

The test conditions were as follows:

• Machine – a special gundrilling machine was used. The drive unit was equipped

with a programmable AC converter to offer variable speed and feed rate con-

trol. The machine contained a high-pressure drilling ﬂuid delivery system capable

of delivering a ﬂow rate up to 120 l/min and generating a pressure of 12 MPa.

312 Tribology of Metal Cutting

The stationary tool-rotating workpiece working method was used in the tests. The

feed motion was applied to the gundrill.

• Work material – because special parts, calender bowls, were drilled, the work mate-

rial was malleable cast iron, Class 80002 having the following properties: hardness,

Brinell HB 241 – 285; tensile strength, ultimate (Rm) – 655 MPa; tensile strength,

yield (Rp0,2) – 552 MPa; elongation at break – 2%.

• Gundrills – specially designed and custom-made gundrills of 35 mm diameter were

used. The material used in the cutting inserts was carbide M30. The parameters of

drill geometry were kept within close tolerance of ±0.2

◦

. The surface roughness R

of the rake and ﬂank faces did not exceed 0.25 µm. Each gundrill used in the tests

was examined at a magniﬁcation of ×25 for visual defect such as chipping, burns

and microcracks. When re-sharpening, the tips were ground back at least 2 mm

beyond the wear marks.

• Drilling ﬂuid (coolant) – a water-soluble gundrill cutting ﬂuid having 7%

concentration.

• Tool life criteria – the average width of the ﬂank wear land VB

=1.0 mm was

selected as the prime criterion and was measured in the tool cutting edge plane

containing the cutting edge and the directional vector of prime motion. However,

excessive tool vibration and/or squeal were also used in some extreme cases as a

criterion of tool life.

The schematic of the experimental setup, shown in Fig. 5.9, is mainly composed of the

deep-hole machine, a Kistler sex-component dynamometer, charge ampliﬁers and Kistler

signal analyzer.

The design matrixes used in GMDH, {¯x

} were obtained as arguments x

were selected

randomly as generated by a random number generator. This assures the uniform density

of probability of occurring of ith argument in jth experiment, which does not depend on

the other argument in the current or previous runs. As such, the design matrix {¯x

} is

considered as n realization of a random vector ¯x having normal density of distribution

of paired scalar products of all factors over the columns of the design matrix due to

the independence of the factors. In the algorithm of GMDH, this is assured using the

Kolmogorov criterion; so the design matrix is generated using a generator of random

numbers until the normal distribution is assured [20].

Five levels of the factors were selected for the study. The levels of the factors and intervals

of factor variations are shown in Table 5.14. The upper level (+2) for the cutting speed,

53.8 m/min (490 rpm), was selected as a result of the preliminary testing and was limited

by the dynamic stability of the shank. As such, the critical rotational speed of the shank

was determined to be 618rpm.

The design matrix shown in Table 5.15 was obtained using the algorithm described

in [20].

Dynamic phenomena. Before any DOE and/or optimization technique is to be

applied, one has to study the inﬂuence of dynamic effects that may dramatically affect

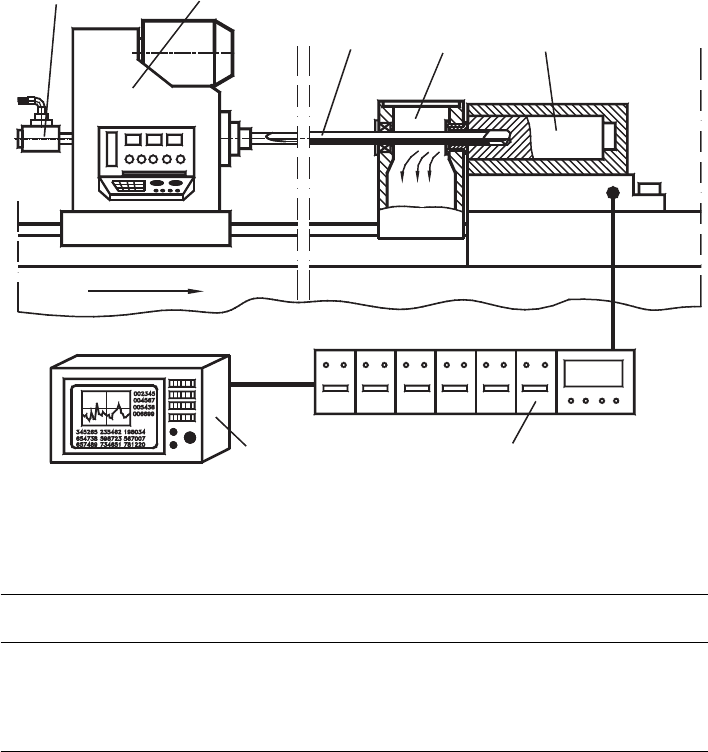
Design of Experiments in Metal Cutting Tests 313

Gundrill spindle headCoolant Coupling

Workpiece

Gundrill Chip Box

Dynamometer

Charge amplifiers

Kistler signal analyzer

Feed motion

Fig. 5.9. Schematic of the experimental setup.

Table 5.14. The levels of factors and their intervals of variation.

Levels x

(

◦

)(

◦

)(

◦

)(

◦

) (mm) (mm) (mm) (mm) (

◦

) (m/min) (mm/rev)

+2 34 24 20 16 1.50 1.50 16.0 17.5 20 53.8 0.21

+1 30 22 17 14 0.75 0.75 14.0 11.5 15 49.4 0.17

0 25 18 14 12 0.00 0.00 11.0 8.75 10 34.6 0.15

−1 22151110−0.75 −0.75 8.75 6.0 5 24.6 0.13

−2 181288−1.50 1.50 6.0 3.5 0 19.8 0.11

the experimental results. If a gundrill works under the condition where resonance

phenomenon affects its performance, no DOE can be used because the response surface

would not be smooth.

Gundrills are intended to drill deep holes and thus their shanks can be of great length.

As a result, the tool has a relatively low static and dynamic rigidity and stiffness. This,

in turn, leads to the process being susceptible to dynamic disturbances, which results in

vibrations. This is particularly true in the case considered, where the properties of the

work material changes along the drill diameter presenting a combination of proeutectoid

white cast iron (HB429-560) and grey pearlite cast iron (HB186-220). As known [24],

these dynamic disturbances lead to the torsional and ﬂexural vibrations of the shank.

314 Tribology of Metal Cutting

Table 5.15. Design matrix and experimental results.

No. R x

Tool life (min)

156+2 −1 −1 −100−10−200 260

288+2 +1 −1 +1 −2 −1 −2 +2 +1 −1 +2 215

387+1 +1 −2 −2 −1 −2 −2 +1 −2 +1 −2 170

432+20−2 +1 −2 −1 −2 +2 −1 −1 +2 251

54400+1 −100+10+2 −2 +1 300

694+2 +1 +1 +

2 +1 +2 −2 +1 −1 −2 −1 273

778+2 −1 +2 +1 −2 −1 −2 +20−1 −1 220

8420+10−1 +2 +1 −1 −1 −2 +1 −2 123

94−1 −1 +1 +2 +1 +2 −2 +1 −2 −2 −1 167

10 41 +2 −2 +2 +200−20+10+1 160

11 54 −1 −1 +1 +

2 +1 +2 −2 +1 −2 +1 −1116

12 65 +2 −1 −2 +1 −2 −1 −1 +20−1 +2 208

13 3 0 +10+2 +1 +1 +1 −2 +1 +10 79

14 11 0 −1 +1 +100−10+1 −1 +1 348

15 48 +2 −1 −2 +1 −2 −10+20−1 0 173

16 43 −1 −200+1 +2 −2 +1 −2 −

2 −1 207

17 40 +1 +2 +1 +2 +1 +2 −2 +1 +2 −1 −1 157

18 66 0 −1 +2 −2 −2 −1 −2 +2 −20+2 185

19 15 −10−2 +100−10−2 −1 +1 368

20 77 −1 −1 +2 −1 +1 +1 −1 −2 −2 −20 77

21 8 0 +2 +2 −2 −2 −10+200+2 157

22 16 +2 −2

−1000+10−2 +1 +1 193

23 25 +1 +1 −10−1 +2 −1 −1 +2 +1 −2 400

24 61 +2 −10+100−10+10+1 200

25 33 +1 +1 +2 −2 −1 +2 −2 +1 +1 −2 +2 166

26 24 +1 −2 +1 +2 +1 +2 −2 +1 −1 +1 −1 187

27 27 +2 +1 −1 −100−10

−200 210

28 52 0 +2 +2 −2 +2 −1 −2 +2 +200 143

29 85 −1 −2 −1 +200−10+10+1 187

30 19 +2 −2 +1 +2 +20000−1 −2 168

31 81 −1 +2 −2 +1 −2 +2 −2 +2 −200 112

32 47 0 −1 −10+1 −2 −2 −2 +2 −1 +197

33 26 +2 −200+20−2 +1 +10−

1 138

34 9 −1 +2 +2 −1 −1 −2 −10−1 −1 −2 253

35 97 +2 −2 +2 +20−1 −1 −1 +1 +1 0 135

36 5 +2 +1 −1 −100−10−200 251

37 49 −1 +20−1 +2 −2 −2 +2 +2 −1 −1 233

38 7 0 −2 +2 +1 +200000−2 122

39 45 −10+2 −2 −2 +2 −1 +2

+1 −1 0 258

40 21 +20000−1 −1 +1 +1 −2 +1 230

41 70 −1 −20−1 +1 −2 +2 +2 +2 −10 60

42 84 +2 +1 −1 −100−10−200 270

4330000+1 −20−10−2 −1 +2 401

44 53 0 +100−1 +1 −20+10−2 390

45 2 0 −1 +1 +2 −2 −1 −1 +2 −2 +1 0 140

46 12 +1 +1

−1 −1 +1 +10−2 +100 126

47 1 +2 −2000−1 +2 −2 +1 −2 +2 103

48 31 +2 +10−1 −1 +2 −2 −10−1 −1 420

49 89 +10+1 +2 +20−2 +1 +20−1 173

50 34 −1 −1 +1 +2 −2 +1 −1 +1 −2 +10 93

continued

Design of Experiments in Metal Cutting Tests 315

Table 5.15. —Cont’d

No. R x

Tool life (min)

51 0 −1 +2 +1 +2000+10−297

52 −1 −20+2 −1 −2 −1 +10−1 −1 183

53 45 +2 +1 −1 −10+2 −2 −2 −1 0 0 272

54 50 +2 −1 +2 +2 −1 −2 +10+2 −10 89

55 72 +1 +1 −2 −2 −2 −1 −2 +2 −1 +1 −2 367

56 14 0 −100+1 −1 −2 +

2 −1 +1 −2 279

57 29 +2000+200+1 −2 −1 −1 187

58 100 −10+1 +1 −1 −1 −2 +10−1 −2 240

59 33 0 −2 −2 −2 +2 +2 +2 +1 −20−166

60 22 +10+1 +1 −1 −1 −2 +1 −2 +1 −2 326

61 80 0 0 −2 −2 −10−2 +2 +1 +1 0 273

62 36 +1 +2 −1

−10+1 −1 −1 −20+1 305

63 67 +1 +1 −1 −1 +1000+10+1 103

64 51 0 0 +1 +1 +2 +1 −2 +20−1 +2 147

6569 000000000 0 0 104

66 55 +1 +1 −1 −1 +1 +1 −2 +10−2 −1 300

67 59 +1 +1 −1 −1 +1 +2 +1 +1 +1 −1 −1 350

68 71 +1 +1 −1 −1 +1 +1

−2 +10−2 −2 315

69 20 +1 −200+1 +2 −2 +1 −1 +1 −1 210

70 74 0 +1 −1 −1 +20−200 0−1 147

71 35 +1 −1 −1 −10+20−10+1 −1 100

72 73 0 +1 −1 −1 −1 +1 −2 −1 +10−2 359

73 28 +1 +1 −1 −10+2 −1 −1 −20+1 310

74 37 −1 +2000+

1 −2 −2 −1 −2 +2 330

75 60 −2 −1 −2 −2 −2 +10+1 −2 +10 67

76 79 +10000+2 +2 −20−2 +2 100

77 83 +2 +1 −1 −100−10−2 0 0 230

78 86 −10+1 +1 +2 −1 +2 +2 −1 +1 +132

79 90 +1 +1 −1 −1 +200+1 −2 −1 −1 284

80 92 +2 +1

−1 −1 −20−10+1 −2 +2 450

81 93 −1 +2 −2 −2 −2 −2 −10+10−1 350

82 62 0 −100+2 +1 +2 −20+1 0 151

83 99 +20−2 −2 +1 +1 −2 −20 0+1 206

84 68 −1 +200+1 +1 +1 −2 0 0 0 152

In order to characterize the dynamics of the gundrilling process, the cutting force and

the amplitude of the shank vibration were measured and analyzed.

For the case considered, the time of one tool revolution was t

=0.19 s (the rotational

frequency of the tool f

=5 Hz, feed f =0.15 mm/rev, cutting speed ν =58 m/min),

the frequency of shank ﬂexural vibration was f

ﬂ

= 320–350 Hz and its amplitude

ﬂ

(

38–46

)

×10

−6

m, the frequency of shank torsion vibration f

= 200–220 Hz in

machining grey cast iron and f

ﬂ

= 640–770 Hz, A

ﬂ

(

2–4

)

×10

−6

m, f

= 300–320 Hz

in machining proeutectoid white cast iron.

The natural frequencies were f

=18.84Hz and f

=23.32Hz (the ﬁrst harmonic) for

the shank of length l

=780×10

−3

m having the ratio of maximum and minimum

316 Tribology of Metal Cutting

rigidities equal to 0.67 due to the V-ﬂute made on the shank for chip removal. As shown,

these natural frequencies do not coincide with those due to the shank vibrations, so

there is no inﬂuence of the resonant phenomenon. This conclusion was corroborated

using different cutting speeds and feeds. The same conclusion was made for torsional

vibrations. As such, the critical angular velocity of the shank was calculated as





+ω



, (5.52)

where ω

x,y

=2πf

n(x,y)

are angular natural frequencies of the shank with respect to the

x and y axes, respectively. It was found that ω

=64.74 s

−1

. Because the experimental

points included in Table 5.15 are to be determined for the following range of the shank

rotational frequency: ω

= 18.86–51.3 s

−1

, it was concluded that there is no inﬂuence

of torsional resonance on the test results.

The following can be stated to summarize the results obtained. The frequency of chip

formation causes forced vibrations of the drill. These vibrations are due to the high

dynamic content of the cutting forces including the cutting torque. As such, the uncut

chip thickness, represented by the cutting feed per revolution, plays an important role.

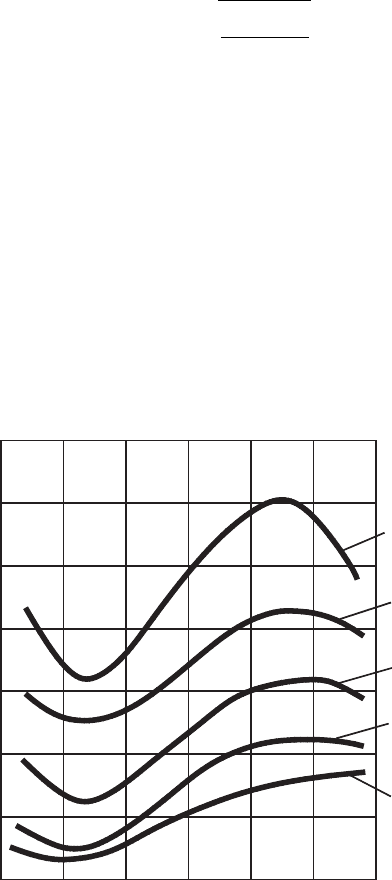
The inﬂuence of this parameter on the axial force is shown in Fig. 5.10, and on the

cutting torque is shown in Fig. 5.11. As follows from these ﬁgures, when the feed

0.40.2 1.00.6 0.8 1.2

n(m/s)

(kN)

1.2

1.4

1.6

1.8

2.0

2.2

2.4

f = 0.21mm/rev

0.17 mm/rev

0.15 mm/rev

0.13 mm/rev

0.11 mm/rev

Fig. 5.10. Inﬂuence of uncut chip thickness (the cutting feed f ) on the axial force.