Astakhov V. Tribology of Metal Cutting

Подождите немного. Документ загружается.

Design of Experiments in Metal Cutting Tests 287

a ﬂow rate up to 75 l/min and generating a pressure of 12 MPa. The stationary

workpiece-rotating tool working method was used in the tests. The feed motion was

applied to the gundrill.

Work material – hot rolled medium carbon steel AISI 1040 was used. The actual chemi-

cal composition has been analyzed using a LECO SA-2000 Discharge-Optical Emission

Spectrometer. Special metallurgical parameters such as the element counts, microstruc-

ture, grain size, inclusions count, etc, were determined using quantitative metallography.

The test bars, after being cut to length (40 mm diameter, 700 mm length), were normalized

to a hardness of HB 200.

Gundrills – gundrills of 12.1 mm diameter were used. The material of their tips was

carbide M 30. The parameters of drill geometry were kept within a close tolerance of

±0.2

◦

. The surface roughness R

of the rake and ﬂank faces did not exceed 0.25 µm.

Each gundrill used in the tests was examined at a magniﬁcation of ×25 for visual defects

such as chipping, burns and microcracks. When resharpening, the tips were ground back

at least 2 mm beyond the wear marks.

Cutting ﬂuid (coolant) – “Shell Garia H” cutting ﬂuid was used in the tests. Its

temperature was maintained at 27 ±3

◦

C and its purity at 10 µm.

Cutting conditions – the optimal cutting speed – 110 m/min (2894 rpm), and feed rate –

90 mm/min were selected using the results of a calibration test for given work and tool

materials. The principles of the ﬁrst metal cutting law (discussed in Chapter 4) were used

to determine the optimal cutting temperature.

Tool life criteria – the average width of the ﬂank wear land VB

=0.4 mm was selected as

the prime criterion and was measured in the tool cutting edge plane containing the cutting

edge and the directional vector of prime motion. However, excessive tool vibration

and/or squeal were also used in some extreme cases.

Eight factors have been selected for this sieve DOE and their intervals of variation are

shown in Table 5.1.

Table 5.1. The level of the factors selected for the sieve DOE.

Factors Approach

angle

(ϕ

)(

◦

)

Approach

angle

(ϕ

)(

◦

)

Flank

angle

(α

)

(

◦

)

Drill point

offset (m

)

(mm)

Flank

angle

(α

)

(

◦

)

Shoulder

dub-off

angle(ϕ

)

(

◦

)

Rake

angle

(γ)

(

◦

)

Shoulder

dub-off

location

(b) (mm)

Code

designation

Upper level

(+)

45 25 25 3.0 12 45 5 4

Lower level

(−)

25 10 8 1.5 7 20 0 1

288 Tribology of Metal Cutting

Table 5.2. Design matrix.

Experiment

number

Factors Tool life (min)

1 ++−−+−+− 7 18.75 11.11

2 +++−−++−16 11.50 11.50

3 −+−−++−+11 11.00 11.00

4 −−+++−−+38 21.75 16.61

5 +−−+−−+−18 13.50 13.50

6 +−+−++−−10 21.75 14.61

7 −−−−−+−+14 14.00 14.00

8 −+−+−−++42 25.75 16.61

9 +−−−−+−+ 9 20.75 20.75

10 −+++−+−−32 15.75 15.75

11 +−+−−−+− 6 17.75 10.61

The design matrix was constructed as follows: all the selected factors were separated

into two groups. The ﬁrst one contained factors x

, form a half-replica

4−1

with the deﬁning relation I = x

. In this half-replica, the effects of

the factors and the effects of their interactions are not mixed. The second half-

replica was constructed using the same criteria. A design matrix was constructed

using the ﬁrst half-replica of the complete matrix and adding to each row of this

replica a randomly selected row from the second half-replica. Three more rows

were added to this matrix to assure proper mixing and these rows were randomly

selected from the ﬁrst and second half-replicas. Table 5.2 shows the design matrix

constructed.

As soon as the design matrix is completed, its suitability should be examined using

two simple rules. First, a design matrix is suitable if it does not contain two identical

columns having the same or alternate signs. Second, a design matrix should not contain

columns whose scalar products with any other column result in a column of the same

(“+”or“−”) signs. The design matrix shown in Table 5.2 was found suitable as it meets

the requirements set by these rules.

The test results are shown in column

as the average tool life calculated over three

independent tests under the test conditions indicated.

5.3.5 Analysis

Analysis of the results of sieve DOE begins with the construction of a correlation (scatter)

diagram shown in Fig. 5.3. Its structure is self-evident. Each factor is represented by a

vertical bar having on its left side, values (as dots) of the response obtained when this

factor was positive (the upper value) while the values of the response corresponding to

lower level of the factor considered (i.e. when this factor is negative) are represented

by dots on the right side of the bar. As such, the scale makes sense only along the

vertical axis.

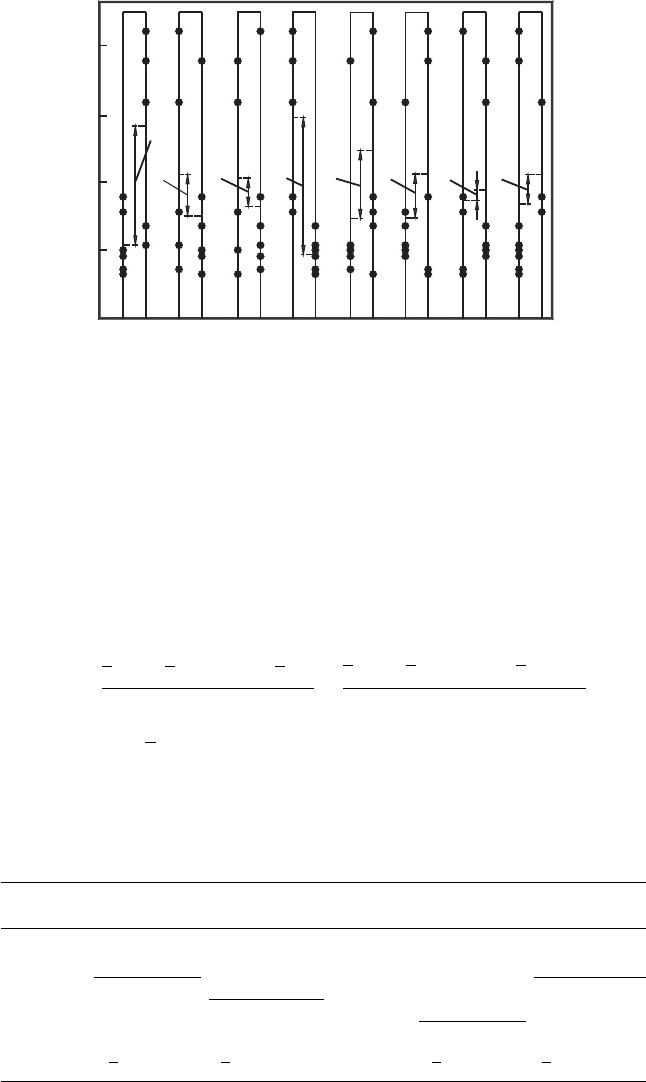
Design of Experiments in Metal Cutting Tests 289

+−

16.4

5.77

3.57 19.7 10.6 6.9

1.2

4.9

Fig. 5.3. Correlation diagram (ﬁrst sieve).

Each factor included in the experiment is estimated independently. The simplest way to

do this is to calculate the distance between the means on the left and right sides of each

bar. These distances are shown on the correlation diagram in Fig. 5.3. As shown, these are

the greatest for factors x

and x

and thus these two factors are selected for the analysis.

The effects of factors are calculated using special correlation tables. A correlation table

(Table 5.3) was constructed to analyze the two factors considered. Using the correlation

table, the effect of each selected factor can be estimated as

1−1

1−3

+···+y

1−n

−

1−2

1−4

+···+y

1−(n−1)

, (5.9)

where m is number of

ys for the factor considered assigned to the same sign (“+”or“−”).

It follows from Table 5.3 that m = 2.

Table 5.3. Correlation table (ﬁrst sieve).

Estimated

factor

−x

Estimated

factor

−x

16 38 7 11

18 42 10 14

32 9

1−1

= 34

1−2

= 112

1−3

= 37

1−4

= 25

1−1

= 17 y

1−2

= 37.3 y

1−3

= 9.3 y

1−4

= 12.5

290 Tribology of Metal Cutting

The effects of the selected factors were estimated using data in Table 5.3 and Eq. (5.10) as

1−1

1−3

−

1−2

1−4

17 + 9.3

−

37.3 + 12.5

=−11.75 (5.10)

1−1

1−2

−

1−3

1−4

17 + 37.3

−

9.3 + 12.5

= 16.25 (5.11)

The signiﬁcance of the selected factors is examined using the Student’s t-criterion,

calculated as

t =



1−1

1−3

+···+y

1−n



−



1−2

1−4

+···+y

1−(n−1)





, (5.12)

where s

is the standard deviation of ith cell of the correlation table deﬁned as

−1

−





(

−1

)

, (5.13)

where n

is the number of terms in the cell considered.

The Student’s criteria for the selected factors are calculated using the results presented

in the auxiliary table (Table 5.4) as follows:



1−1

1−3



−



1−2

1−4





(17+9.3)−(37.3+12.5)

3.52

=−6.68 (5.14)



1−1

1−2



−



1−3

1−4





(17+37.3)−(9.3+12.5)

3.52

=9.23 (5.15)

Table 5.4. Calculating t-criterion.

Cell number

1−i



1−i



1−i

1 34 1156 580 2 2.00 1.00

2 112 12544 4232 3 25.33 8.44

3 37 1369 351 4 2.92 0.73

4 25 625 317 2 4.50 2.25

Design of Experiments in Metal Cutting Tests 291

A factor is considered to be signiﬁcant if t

, where the critical value, t

for the

Student’s criterion is found in a statistical table for the following number of degrees of

freedom

−k =11−4=7, (5.16)

where k is the number of cells in the correlation table.

For the case considered, t

99.9

= 5.959 (Table 5.7 in [16]) so that the factors considered

are signiﬁcant with a 99.9% conﬁdence level.

The procedure discussed is the ﬁrst stage in the proposed sieve DOE and thus it is

referred to as the ﬁrst sieve. This ﬁrst sieve allows the detection of the strongest factors,

i.e. those factors that have the strongest inﬂuence on the response. After these strong

linear effects are detected, the size of “the screen” to be used in the consecutive sieves

is reduced to distinguish less strong effects and their interactions. This is accomplished

by the correction of the experimental results presented in column

of Table 5.2. Such

a correction is carried out by adding the effects (with the reverse signs) of the selected

factors (Eqs. (5.11) and (5.12)) to column

of Table 5.2, namely, by adding 11.75 to

all the results at level “+x

” and −16.25 to all the results at level “+x

.” The corrected

results are shown in column y

of Table 5.2. Using the data from this table, one can

construct a new correlation diagram shown in Fig. 5.4, where, for simplicity, only a few

interactions are shown although all possible interactions have been analyzed. Using the

approach described above, a correlation table (second sieve) was constructed (Table 5.5)

and the interaction x

was found to be signiﬁcant. Its effect is X

=7.14.

After the second sieve, column y

was corrected by adding the effect of X

with the

opposite sign, i.e. −7.14 to all the results at level +x

. The results are shown in

+− +− +− +− +− +− +− +− +− +− +− + −

5.07

4.54

6.82

Fig. 5.4. Correlation diagram (second sieve).

292 Tribology of Metal Cutting

Table 5.5. Correlation table (second sieve).

Estimated factor +x

−x

11.5 18.75 18.75 11.5

11 25.75 25.75 11

15.75 15.75

2−1

=22.5

2−2

=60.25

2−3

=44.5

2−4

=38.25

2−1

=11.25 y

2−2

=20.08 y

2−3

=22.25 y

2−4

=12.75

Estimated factor + x

−x

14 21.75 21.75 13.50

20.75 13.5 21.75 14

−x

17.75 21.75 17.75 20.75

2−5

=52.5

2−6

=57

2−7

=61.25

2−8

=48.25

2−5

=17.5 y

2−6

=19 y

2−7

=20.42 y

2−8

=16.08

column y

of Table 5.2. Normally, the sieve of the experimental results continues while

all the remaining effects and their interactions become insigniﬁcant, at say a 5% level

of signiﬁcance if the responses were measured with high accuracy and a 10% level if

not. In the case considered, the sieve was ended after the third stage because the analysis

of these results showed that there are no more signiﬁcant factors or interactions left.

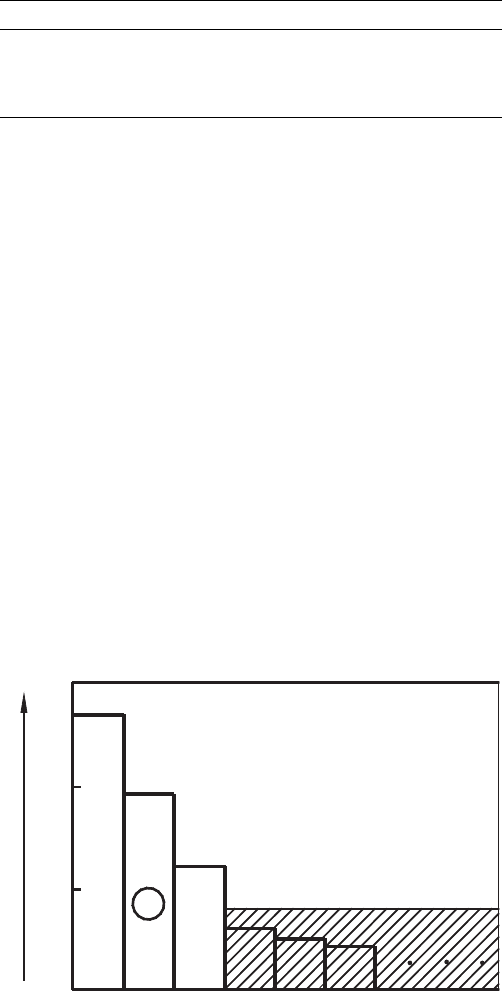
Figure 5.5 shows the scatter diagram of the test discussed. As shown in the ﬁgure, the

scatter of the analyzed data reduces signiﬁcantly after each sieve, so normally three

sieves are sufﬁcient to complete the analysis.

Tool life, min

Fig. 5.5. Scatter diagram.

Design of Experiments in Metal Cutting Tests 293

Table 5.6. Summary of the sieve test.

Stage of sieve Distinguished factor Effect t-Criterion

Original data x

−11.5 6.68

16.25 9.23

First sieve x

7.14 4.6

Second sieve – – –

The results of the proposed test are summarized in Table 5.6. Figure 5.6 shows the

signiﬁcance of the effects distinguished in terms of their inﬂuence on tool life. As shown,

two linear effects and one interaction having the strongest effects were distinguished. The

negative sign of x

shows that tool life decreases when this parameter increases. The

strongest inﬂuence on tool life has the drill point offset m

While the linear effects distinguished are known to have strong inﬂuence on tool life, the

interaction x

distinguished has never before been considered in any known studies on

gundrilling.

5.3.6 Concluding remarks

The proposed sieve DOE allows experimentalists to take into consideration as many

factors as needed. Conducting a relatively simple sieve test, the signiﬁcant factors and

their interactions can be distinguished objectively and then used in the subsequent full

DOE. Such an approach allows one to reduce the total number of tests dramatically

without losing any signiﬁcant factor or factor interaction. Moreover, interactions of any

order can be easily analyzed. The proposed correlation diagrams make such an analysis

simple and self-evident.

etc.

−

Effect

Fig. 5.6. Signiﬁcance of the effects distinguished by the sieve DOE (Pareto analysis).

294 Tribology of Metal Cutting

Three factors are found to have a signiﬁcant effect on tool life in gundrilling. As was

expected, the strongest inﬂuence has the drill point offset m

. It was also found that tool

life decreases when the approach angle of the outer cutting edge increases.

The interaction x

distinguished has never before been considered in the known

analyses on tool life in gundrilling. Using this factor and results of the complete

DOE, a new geometry of gundrills has been developed.

5.4 2

Factorial Experiment, Complete Block

This type of experiments are utilized to investigate the effects of one or more factors

on the response. When an experiment involves more than one factor, these factors can

inﬂuence the response individually as well as jointly. In the case of one factor-at-a time

experiment, the selected experimental methodology does not allow proper assessment of

the joint effects of the factors involved.

Factorial experiments conducted in completely randomized designs are especially useful

for evaluating the joint factor effects. Factorial experiments include all possible factor

combinations in the experimental design. Completely randomized designs are appropriate

when there are no restrictions on the order of testing.

The mathematical description of the object under study in the vicinity of zero point can

be obtained by varying each factor at two levels distinguished from the zero level by

the interval of variation. When the experiment includes all possible non-repeated factor-

level combinations, it is called as the complete block. The number of such combinations

is N = 2

5.4.1 Regression model and design matrix

Consider the case where three factors are taken into consideration. As such we deal with

factorial experiment that demonstrated its usefulness in metal cutting tests [3,9]. The

regression equation for this test is



y =E



i=1

˜x

i,j=1

˜x

123

˜x

(5.17)

The complete block enables one to obtain the separate (non-mixed) estimates for all

coefﬁcients b of this model. This is the major advantage of this type of DOE.

Obtaining the mathematical model in the form of Eq. (5.18) includes the following stages:

• Design of experiment: statement of the problem; selection of the response and fac-

tors to be involved; determining the levels of the factors, selection of the sequence

of the factor-level combinations – construction of the design matrix; selection

Design of Experiments in Metal Cutting Tests 295

Table 5.7. Treatment combinations and effects in 2

factorial experiment.

Point of matrix (u) x

1 +−−− + + + −

2 ++−− − − + +

3 +−+− − + − +

4 +++− + − − −

5 +−−+ + − − +

6 ++−+ − + − −

7 +−++ − − + −

8 ++++ + + + +

of the number of observations to be taken at each point of the design matrix; selection

of a regression model to describe the experimental results.

• Experiment itself as a series of tests; data collection in each test.

• Evaluation and analysis: examination of the statistical signiﬁcance of the model

coefﬁcients; examination of the homogeneity of the row variances; examination of

the adequateness of the mathematical model obtained.

Using the code values (+1, −1), the experimental conditions can be written as the design

matrix, where the rows correspond to different tests and the columns correspond to the

different code values of the factors [2]. The design matrix for a 2

factorial experiment

(complete block) is shown in Table 5.7. In this table, columns x

, x

and x

form the

design matrix because they directly set up the test conditions. Further to the right, the

columns for interactions x

, x

and x

are placed. These are to be used

for the estimation of the factor interactions. A pseudo-variable x

is also added for the

estimation of coefﬁcient b

. The value of x

(+1) is the same in all rows.

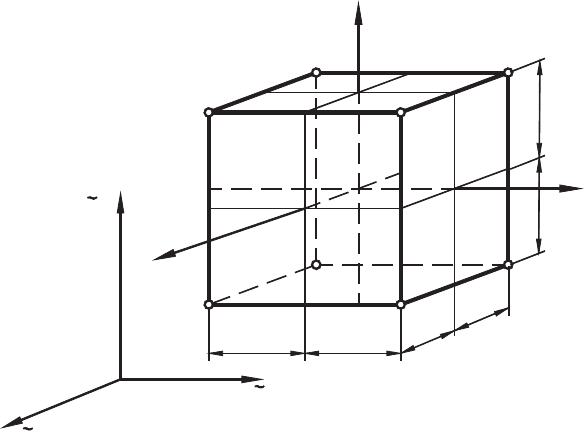
The design matrix described can be represented graphically, as shown in Fig. 5.7. New

coordinate axes x

, x

are drawn through the origin 0 parallel to the original axes of

the factors. The origin 0 corresponds to the basic (zero) level of the factors. The scale

of the new coordinate system is selected so that the intervals of variation of each factor

are equal to 1. Therefore, the design is a cube with the eight runs forming the corners of

the cube, as shown in Fig. 5.7.

The following notation of tests is normally used. A number u (u =1,2,..., 8) is attributed

to each point in the design matrix. The tests have double numbering, the ﬁrst number

shows the point in the design matrix; the second is a number of the repetition in this

point. The number of repetitions at the same point is designated by r

> 1). For

example, y

is the response obtained in the third test conducted at the second point of

the design matrix.

5.4.2 Properties of 2

factorial experiment, complete block

There are several important properties of a complete block design matrix making this

matrix very suitable for obtaining the mathematical models using the experimental data.

296 Tribology of Metal Cutting

−1

−1 +1

Fig. 5.7. Graphical representation of the 2

design.

First two directly stem from the way the matrix is constructed. The ﬁrst property is the

matrix symmetry relative to the center of the experiment. It can be described as follows:

the sum of elements of each vector-column (except that for x

) is equal to zero, i.e.

u=1

=0,i=1,2,...,2

−1, (5.18)

where u, m are the number of a point and the total number of points in the matrix,

respectively.

The second property is that the sum of squares of the element of each vector-column is

equal to the number of the points in the matrix, i.e.

u=1

=m, i =1,2,...,2

−1 (5.19)

The third property is called the orthogonality of the design matrix. Orthogonality in such

a context means that the sum of the product of entries of any two vector-columns in the

matrix is equal to zero, i.e.

u=1

=0,i=j, i, j =1,2,...,2

−1 (5.20)