Astakhov V. Tribology of Metal Cutting

Подождите немного. Документ загружается.

Energy Partition in the Cutting System 77

Workpiece

Chip

Cutting

direction

Tool

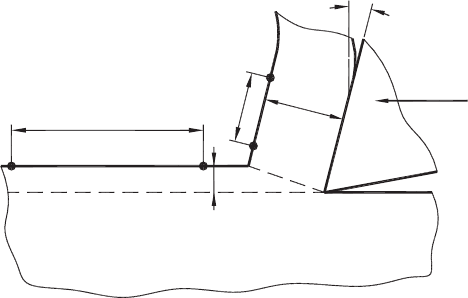
Fig. 2.2. Scheme of chip deformation in cutting (after Astakhov [28]).

deformation encountered in metal cutting, it seems only logical to verify the justiﬁcation

of its usage as such a measure.

As discussed in Chapter 1, Merchant [15] proposed the expression for the shear strain

(Eq. (1.14)), which should be actually called the ﬁnal shear strain [2]. As discussed in

Chapter 1, when ζ = 1, the chip thickness is equal to the uncut chip thickness (Eq. (2.6)),

the shear strain, calculated by Eq. (1.14) remains very signiﬁcant. For example, when

ζ = 1, the rake angle γ =−10

◦

, Eq. (1.14) yields ε = 2.38; when ζ = 1, γ = 0

◦

then

ε = 2; when ζ = 1, γ =+10

◦

then ε = 1.68. This reveals a contradiction; as CCR,

considered to be a measure of plastic deformation, indicates that no plastic deformation

occurs while the ﬁnal shear strain remains signiﬁcant. Moreover, if one compares the

strains calculated using Eq. (1.14) with the standard mechanical characteristic of work

materials, he can conclude that the strains in metal cutting signiﬁcantly exceed (by 200–

1000%, depending on the rake angle) the strains at fracture of even very ductile materials

[11]. To the best of the author’s knowledge, no study pointed out and/or explains this

abnormality in the mechanical properties of work materials in machining.

At this point, it is worthwhile to explain that the equation of ﬁnal shear strain (Eq. (1.14))

was derived using purely geometrical considerations, i.e. it does not consider the change

in internal energy of the chip due to the change in chip density, the increased dislocation

concentration, or the stress imposed on the boundaries of the grains, etc., even though

all of these increase the shear strength of the chip compared to the initial work material.

Shear strain, according to Eq. (1.14), is deﬁned only by the changes in the dimensions of

a deformed body as compared to its original dimensions. As CCR indicates that there is

no change in the dimensions, there is no “geometrical deformation,” so the strain should

be equal to zero. However, this does not follow from the known equation for strain.

Astakhov [2] pointed out that when properly measured, CCR directly reﬂects the ﬁnal

plastic deformation of the chip. Although this parameter was widely used in metal cutting

tests of the past [12], it was always considered as a secondary parameter to provide

78 Tribology of Metal Cutting

qualitative support to certain conclusions. Since the real signiﬁcance of this parameter

has not been revealed, it was gradually abandoned in metal cutting studies because

nobody could explain the meaning of the results obtained. For example, although Shaw

dedicated a full chapter to the analysis of plastic deformation in metal cutting, in his

book, this parameter is not even mentioned [9]. The same can be said about the books by

Trent and Wright [18], Oxley [14] and Gorczyca [16]; and Altintas [19] just mentioned

its deﬁnition in the consideration of the single-shear plane model; Childs et al. [20]

mentioned this parameter as related to the friction coefﬁcient at the tool–chip interface.

Not a single modern study on metal cutting correlates this parameter with the amount of

plastic deformation in metal cutting.

2.4.2 Work of plastic deformation

The external forces applied, which result in the work done over the system, are not

uniformly distributed over the system’s components. To deﬁne the action of an external

force on the different regions of a body, the notion of stress is used. It is considered

that if a body is subjected to a general system of body and surface forces, stresses of

variable magnitude and direction are produced through the body. The distribution of these

stresses must be such that the overall equilibrium of the body is maintained; furthermore,

equilibrium of each element in the body must be maintained.

Consider an inﬁnitesimal element of parallelpiped form with its faces oriented parallel

to the coordinate planes, as shown in Fig. 2.3. When the body and inertia forces are

insigniﬁcant, the following three differential equations of force (stress) equilibrium are

Fig. 2.3. Stresses acting on elemental free body.

Energy Partition in the Cutting System 79

obtained [2,21]

∂σ

∂x

∂τ

∂y

∂τ

∂z

= 0 (2.7)

∂τ

∂x

∂σ

∂y

∂τ

∂z

= 0 (2.8)

∂τ

∂x

∂τ

∂y

∂σ

∂z

= 0 (2.9)

When a stress ﬁeld applied to a body and, as a result, the relative position of its parts is

changed, the body is deformed or strained. A deformed state in a point can be represented

by the strain components if the projections u

and u

, of the displacement of this

point into the corresponding coordinate planes are known

∂u

∂x

∂u

∂y

∂u

∂z

∂u

∂y

∂u

∂x

∂u

∂z

∂u

∂y

∂u

∂x

∂u

∂z

, (2.10)

where e

, e

and e

are the direct strains, γ

, γ

and γ

are the engineering shear

strains.

Using the generalized Hooke’s law, one can write the following relationship between the

strains and stresses [21]



−ν



+σ





−ν

(

+σ

)





−ν



+σ



(

1 + ν

)

(

1 + ν

)

(

1 + ν

)

, (2.11)

where E is the modulus of elasticity and ν

is the Poisson’s ratio.

The imbalanced external forces applied to a body cause its deformation and thus lead

to the displacement of its points until the equilibrium is established. As such, a certain

amount of energy is absorbed. This energy depends on the work done in displacement

of all points of the body. Such work can be calculated by integrating the work per

unit volume. The work per unit volume done in the displacement of each point of

the body is calculated as the product of the generalized force acting on a point and the

change of the generalized displacement of this point caused by this force. The von Mises’

stress [21]

√





−σ





−σ



(

−σ

)



+τ



(2.12)

80 Tribology of Metal Cutting

was considered as the generalized force and the equivalent strain

√



−e

)

+(e

−e

)

+(e

−e

+6(e

)



(2.13)

can be considered as the generalized displacement.

Because the elementary work is dA = σ

, the total work done over a volume V is then

calculated as [2]

A =



dV (2.14)

As mentioned, CCR is used for the estimation of plastic deformation in experimental

studies on the metal cutting process [2]. As such, the distribution of the mechanical

energy over the cross section of the chip is assumed to be uniform. Using such an

assumption, an engineering equation to calculate the energy spent in cutting can be

obtained. If it is so, the CCR can be used to compare the power consumed in cutting

of the same work material using different cutting processes. Moreover, the amount of

power consumed, allows the comparison of machining different work materials.

The engineering equation mentioned for the estimation of energy spent in the cutting

process can be obtained using the assumption of homogeneous distribution of strain in

Eqs. (2.12)–(2.14). To derive it, the xyz coordinate system is set so that the y axis is

directed along the chip length (L

), the x axis is directed along the chip width (d

)

and the z axis is directed along its thickness (t

). As such, the following expressions for

the components of the true strain along the coordinate axes introduced can be written

accounting for the deﬁnition of CCR, ζ [2]

= ln ζ

=−ln ζ

(2.15)

As shown by Astakhov [2], in orthogonal cutting, the direction of the principal stress

coincides with the coordinate system introduced. Then, Eq. (2.13) could be re-written

accounting for Eq. (2.15) as

√



(

−ln ζ

)

(

ln ζ

−ln ζ

)

(

ln ζ

+ln ζ

)



(2.16)

As shown in [2], if the chip parameters are properly measured in the orthogonal cutting

test, then ζ

= 1 and ζ

= ζ

= ζ, and therefore plane strain condition is the case in

such a process. Hence,

= 1.15 ln ζ (2.17)

In the coordinate system considered, stress components σ

and σ

do not depend on the

x coordinate (measured along chip width) and the σ

component is determined as

= 0.5(σ

+σ

) (2.18)

Energy Partition in the Cutting System 81

Substituting these results in Eq. (2.15), one can obtain

√





−0.5



+σ





0.5



+σ



−σ





−σ





(2.19)

or after simpliﬁcation

= 0.87(σ

−σ

) (2.20)

A true stress–strain curve is known as the ﬂow curve because it gives the stress required

to cause the metal to ﬂow plastically to any given strain [11]. Although many attempts

have been made to ﬁt mathematical equations to this curve [22], the most common is a

power expression of the form

σ = Kε

, (2.21)

where K is the stress at ε = 1.0, n is the strain-hardening coefﬁcient, and is the slope of

a log–log plot of Eq. (2.21).

Substitution of Eq. (2.21) into Eq. (2.20) yields

= 0.87



Kε

−Kε



= 0.87K



−ε



= 0.87K



(

ln ζ

)

−

(

ln ζ

)



= 0.87K2

(

ln ζ

)

= 1.74K

(

ln ζ

)

(2.22)

Because it was assumed that the chip has uniform deformation, the elementary work

spent over plastic deformation of a unit volume of the work material is calculated as



σdε =

Kε

n+1

n + 1

k(1.15 lnζ)

n+1

n + 1

(2.23)

The result obtained is of great signiﬁcance to the experimental studies in metal cutting,

because it correlates in a simple and physically grounded manner, the work of plastic

deformation done in cutting with a measurable, post-process characteristic of the cutting

process such as the CCR. Knowing the elementary work, the total work done by the

external force applied to the tool is then calculated as

A = A

νf d

(2.24)

A series of cutting tests were carried out to compare the power consumption under

different cutting conditions. All the tests were conducted using the same cutting feed

f = 0.07 mm/rev and the depth of cut d

= 1 mm. Three different types of work

material listed in Table 2.1 were used in the tests. For each work material, the inﬂuence

of cutting speed on CCR was determined and the elementary work spent over plastic

deformation of the work material was calculated using Eq. (2.23).

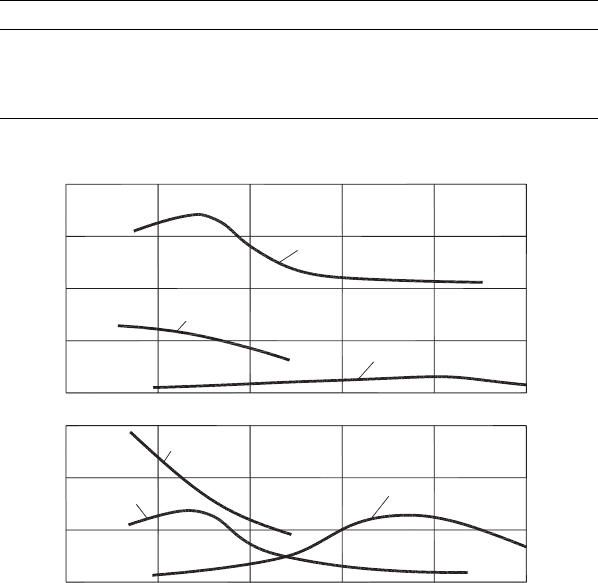
The test results are shown in Fig. 2.4. As shown, although CCR is the greatest in the

machining of copper and lowest in the machining of steel, the elementary work is the

82 Tribology of Metal Cutting

Table 2.1. Work materials used in the tests.

Material K (GPa) n

AISI steel E52100, HB280 (0.981.10% C, 1.45% Cr,

0.35% Mn)

1.34 0.25

Copper (99.7%) 0.40 0.24

Aluminum 1050–0, HB 21 0.14 0.27

(GJ)

213

n (m/s)

Fig. 2.4. Inﬂuence of cutting speed on CCR and the work done in plastic deformation: 1 – AISI

steel E52100, 2 – copper and 3 – aluminum 1050–0 (after Astakhov [28]).

greatest for steel. In other words, the energy per unit volume spent in the machining of

steel is the greatest, which results in a much higher amount of heat generated and in

more signiﬁcant tool wear. This conclusion is supported by multiple facts known from

the everyday practice of machining.

It follows from Fig. 2.4 that CCR is a representative measure of the work of plastic defor-

mation in metal cutting. For steel E52100, CCR varied within 67% under experimental

conditions used in the test while the elementary work varied within 89%. For copper

and aluminum, CCR varied within 60 and 55%, respectively, while the elementary work

varied within 55 and 71%, respectively.

The accuracy of estimation of the work done in plastic deformation can be improved if

one accounts for the change in the parameters K and n (Eq. (2.23)) depending on the

cutting speed (strain rate) and actual temperature in the chip formation zone. As such,

two important issues should be accounted for.

Energy Partition in the Cutting System 83

• The ﬁrst is that orthogonal metal cutting is essentially a cold-working process

because the velocity of heat conduction is much lower than the cutting speed, and

thus the thermal energy generated in the plastic deformation of the layer being

removed does not affect the resistance of the work material to cutting ahead of the

tool. In real cutting operations such as turning or drilling, only the residual heat

from the previous position of the cutting tool may affect the temperature of the

deformation zone at the current tool position.

• The second issue concerns the strain rate in metal cutting. As considered by many

specialists in the ﬁeld, there is no need for special high strain rate tests to determine

the value of constants K and n in Eq. (2.23).

The method proposed for estimating the work of plastic deformation in metal cutting

gives a new meaning to CCR. In the sense implied, it can be used as a prime parameter

for the optimization of the metal cutting process because when considered together with

the work of plastic deformation, it reveals the energy spent in cutting. Moreover, CCR is

a post-process parameter and thus there are a number of simple though forgotten ways to

measure this parameter accurately in metal cutting. Some simple methods of measuring

CCR that can be used in shop ﬂoor for the optimization of practical cutting operations

are discussed in Appendix B.

2.4.3 Inﬂuence of cutting speed

It is well known that the cutting speed has the strongest inﬂuence on CCR [2,12].

Figure 2.5 shows an example of such an inﬂuence in the format commonly used in

metal cutting studies [12]. The explanation of the shape of the graphs shown in Fig. 2.5

is still the same as it was 50 years ago when only the data obtained at low cutting speeds

were available. The built-up edge is believed to be the prime factor affecting the shown

dependencies [12]. The problem with this explanation is that the built-up edge does not

exist at the speeds used to obtain data shown in Fig. 2.5. Therefore, another physically

1.5

1234

2.0

2.5

f = 0.12 mm/rev f = 0.18 mm/rev

f = 0.48 mm/rev f = 0.76 mm/rev

Fig. 2.5. Inﬂuence of cutting speed on CCR. Operation – longitudinal turning, workpiece diameter

– 100 mm, work material – steel AISI 1045, tool material – carbide P20, tool cutting edge angle

= 60

◦

, normal rake angle γ

= 7

◦

and depth of cut d

= 3.5 mm (after Astakhov [28]).

84 Tribology of Metal Cutting

sound explanation should be provided to help specialists to appreciate the meaning of

CCR in the optimization of the metal cutting process.

The cutting speed has the strongest inﬂuence on the energy distribution in the cutting

system because it determines the intensity of the heat sources. Increasing the cutting

speed leads to a decrease in the plastic deformation in the chip formation zone and, as a

result, a lesser portion of the applied mechanical energy converts into heat (or thermal

energy) in this zone so that the chip is “born” less hot. Simultaneously, however, the

amount of heat generated at the tool–chip and tool–workpiece interfaces increase due to

the increased chip velocity so that the chip, sliding over the tool rake face, receives more

thermal energy. The total energy absorbed by the chip is equal to the sum of the thermal

energies (heat) gained by the chip in its formation, i.e. during the plastic deformation of

the layer being removed and that transferred into the chip from the tool–chip interface.

The average temperature of the chip can be represented as [2,12]

ch−aν

= C

, 0 <x

< 1 (2.25)

Multiple tests of different metallic materials showed [2,12] that if there were no metal-

lurgical (chemical) transformations occurring on heating a material from temperature θ

to θ

, the elasticity modulus changes according to the following exponential equation

= E

(

−θ

)

, (2.26)

where α

is a constant for a given material.

An increase in the thermal energy transferred to the chip with increasing cutting speed

results in lowering the rigidity of the chip and its “effectiveness” as a lever to transmit

the bending moment to the chip formation zone. As a result, the compressive stress takes

a greater share in the combined stress in the chip formation zone. As such, the required

external energy applied to the cutting system and that spent on plastic deformation of the

layer to be removed, increases because this new state of stress in the deformation zone

requires more energy for the separation of the layer being removed.

In cutting, the external force is applied to the tool, and it is transmitted from its rake

face into the chip formation zone through the chip. As such, certain energy losses occur

in such a transmission. To estimate these losses, consider the work done by the force

applied to the chip from the tool rake face. If l

designates the elementary length of the

chip, then the work done over the chip by the force from the tool rake face consists of

the work done by the bending moment and the compressive force

Qdl

, (2.27)

where M is the bending moment

(

=SL

)

as per Fig. 1.20(d), E

is the elasticity modulus

of the material of the chip, I

is the second moment or moment of inertia of the cross

section of the chip, Q is the compressive force as per Fig. 1.20(d) and A

is the cross-

sectional area of the chip.

Energy Partition in the Cutting System 85

If the elasticity modulus of the material of the chip tends to inﬁnity, then it follows from

Eq. (2.27) that dW

= 0, i.e. all the energy applied to the cutting tool is transmitted

through the chip without losses. In reality, however, the modulus of elasticity is a ﬁnite

value and, moreover, it decreases with the rise of temperature of the chip (Eq. (2.26))

so that part of the energy transmitted through the chip is spent on its deformation. As

such, the work, of plastic deformation and fracture of the layer to be removed, done by

the external force is calculated as

dW = dW

−dW

(2.28)

As discussed above, according to the energy theory of failure, a given volume of the work

material fails when the critical internal energy is accumulated in this volume. As a result,

dW can be considered as a constant for a given cutting system. According to Eq. (2.28),

to keep dW constant when dW

increases, the energy supplied to the cutting tool by

the external force (dW

), should be increased. Flexural and compression rigidities of the

chip, E

and A

, respectively, decrease with temperature according to Eq. (2.26).

Therefore, an increase in the heat ﬂow into the chip with the cutting speed leads to an

increase in dW

, i.e. in increasing the energy needed for chip formation.

The cutting speed affects the shape and dimensions of the chip formation zone [2,12] or

the extent of the region of plastic deformation ahead of the tool. When the cutting speed

increases, this region of plastic deformation becomes smaller. Instead, the elastically

deformed or rigid zone starts to occupy more and more cross-sectional area of the chip.

The emergence of this elastically deformed region can be thought of as the formation of

force ampliﬁcation through a lever. In other words, the formation of the elastic zone leads

to a decrease in the energy required from the tool for chip formation. It is equivalent

to an increase in I

and A

in Eq. (2.27) and leads to a decrease in the chip plastic

deformation. Moreover, it is possible to limit the region of plastic deformation near

the cutting edge to certain optimum limits so that the chip-cantilever can transmit the

maximum energy from the cutting tool to this region. As such, the contribution of the

bending stress in the formation of the combined stress in the chip formation region is

the greatest.

The formation of the elastically deformed part of the chip begins at a certain cutting

speed at which a dramatic change in the energy spent in the plastic deformation should

be observed. Then, as the cutting speed increases, the dimensions of the elastic region

increase, stabilizing at a certain point because the dimensions of the elastic region cannot

exceed those of the layer to be removed.

The strain rate can be thought of as a ratio of the deforming velocity and the length of

deformation. In cutting, the cutting speed (ν) is the velocity of deformation of the layer

being removed. As shown in [2], the strain rate can be represented as a function of this

velocity as

˙e =

, (2.29)

where L

is the length of the deformed specimen in the direction of the cutting speed.

86 Tribology of Metal Cutting

On the other hand, by deﬁnition, the strain rate is deﬁned as

˙ε =

dε

dτ

(2.30)

Combining Eqs. (2.29) and (2.30), one can obtain the following differential equation

dε

dτ

(2.31)

which has the following solution

= ε +C

, (2.32)

where ε = ln ζ is the true strain, C

is a constant equal to the value of ln ζ when ν = 0.

Finally, the correlation between the CCR and the cutting speed (deformation velocity)

can be obtained from Eq. (2.32) as

ζ = e



−

τν



(2.33)

As follows from Eq. (2.33), CCR decreases with the cutting speed according to the

exponential curve.

The foregoing analysis suggests that the cutting speed inﬂuences the energy spent on the

deformation of the chip through the temperature, dimensions of the deformation zone

adjacent to the cutting edge and the velocity of deformation. The impacts of these factors

can be summarized as follows (Fig. 2.6):

• The inﬂuence of chip temperature on the work done over the chip in its plastic

deformation can be estimated using CCR as follows: increasing the cutting speed

Chip compression ratio

Cutting speed

Fig. 2.6. Formation of the resultant dependence of CCR on the cutting speed (afterAstakhov [28]).