ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation
Подождите немного. Документ загружается.

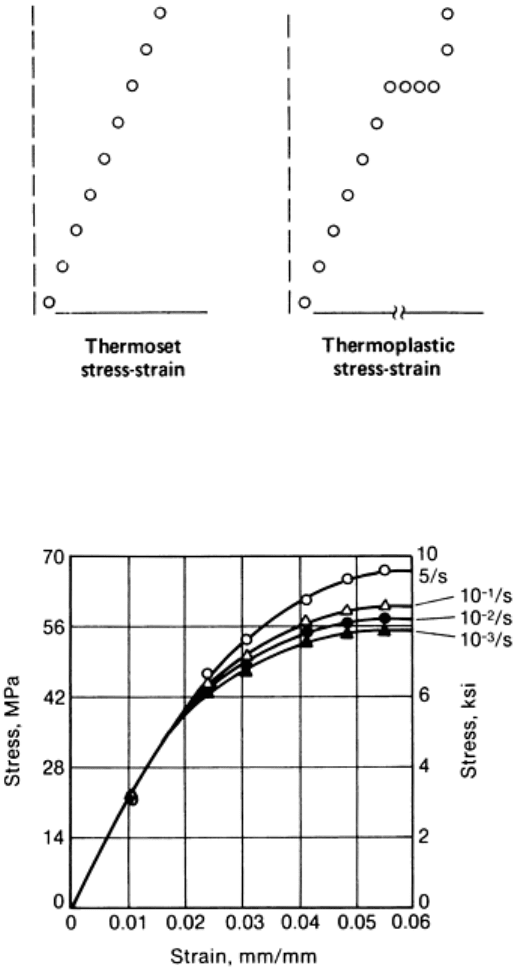
strain curve than in conventional thermosets, which are more rigid networks with much less area under the
stress-strain curve.
Fig. 7 Thermoset versus thermoplastic stress-strain behavior
Because the deformation of thermoplastics is time-dependent, careful control of test duration and strain rate is
important. A slower test (i.e., one at a low strain rate) allows more time for deformation and thus alters the
stress-strain curve and lowers the tensile strength. This effect is shown in Fig. 8 for polycarbonate.
Fig. 8 Stress-strain curves for rubber-modified polycarbonate at room temperature as a function of
strain rate
Short-term tensile properties are usually measured at a constant rate of 0.5 cm/min (0.2 in./min). It is
recommended by the American Society for Testing and Materials (ASTM) that the speed of testing be such that
rupture occurs in 0.5 to 5 min. Test coupons are either injection molded or compression molded and cut into a
standard shape. In practice, injection-molded coupons are usually used.
The history of the plastic sample has some influence on tensile properties. A tensile bar prepared by injection
molding with a high pressure tends to have higher tensile strength. A material that has been oriented in one
direction tends to have a higher tensile strength and a lower elongation at break in the direction of orientation.
In the direction perpendicular to the orientation, tensile strength is consistently lower. In a crystallizable
material, stretching usually increases crystallinity.
Because the mechanical properties are sensitive to temperature and absorbed moisture, conditioning procedures
for test specimens have been developed. These procedures are defined in ASTM D 618 and ISO 291.
Tensile Modulus. Because plastics are viscoelastic materials, stress-strain relationships are nonlinear and
curved (usually convex upward). The curvature arises from two causes. First, the deflection axis is
simultaneously a time axis, and during the test, molecular relaxation processes continuously reduce the stress
required to maintain any particular strain. Second, as the strain increases, the molecular resistance to further
deformation decreases; that is, the effective modulus falls.
The degree of curvature depends on the material and the test conditions. At high strain rates and/or low
temperatures, the stress-strain relationship usually approximates to a straight line. However, if the curvature is
pronounced, the stress-strain ratio must be either a tangent modulus or a secant modulus. The tangent modulus
is the instantaneous slope at any point on the stress-strain curve, while the secant modulus is the slope of a line
drawn from the origin to any point on a nonlinear stress-strain curve. These moduli may be conservative or
nonconservative, relative to one another and depending on the location on the curve.
The accuracy of modulus data derivable from a stress-strain test may be limited, mainly because axiality of
loading is difficult to achieve and because the specimen bends initially rather than stretches. In addition, the
origin of the force-deflection curve is often ill defined, and the curvature there is erroneous, to the particular
detriment of the accuracy of the tangent modulus at the origin and, to a lesser degree, that of the secant moduli.
Under the very best experimental conditions, the coefficient of variation for the modulus data derivable from
tensile tests can be 0.03 or lower, but more typically it is 0.10 (Ref 10). If the strain is derived from the relative
movement of the clamps rather than from an extensometer, the error in the calculated value of the tangent
modulus at the origin can be 100% (Ref 9).
Yield stresses of plastics depend on a variety of molecular mechanisms, which vary among polymer classes and
may not be strictly comparable. However, regardless of the underlying mechanisms, yield stress data have a
low coefficient of variation, typically 0.03 (Ref 10). Brittle fracture strengths are much more variable, reflecting
the distributions of defects that one might expect. The scatter due to the inherent defects in the materials is
exacerbated when elongations at fracture are small because poor and variable alignment of the specimens
induces apparently low strengths if the theoretical stresses are not corrected for the extraneous bending in the
specimens (Ref 10).
Long-term uniaxial tensile creep testing of plastics is covered in ASTM D 2990 and ISO 899. ASTM D 2990
also addresses flexural and compressive creep testing. For the uniaxial tensile creep test in D 2990, the test
specimen is either a standard type I or II bar, per ASTM D 638, that is preconditioned to ASTM D 618
specifications. The test apparatus is designed to ensure that the applied load does not vary with time and is
uniaxial to the specimen. As with other tests, the test specimen must not slip in or creep from the grips. The
load must be applied to the specimen in a smooth, rapid fashion in 1 to 5 s. If the test is run to specimen failure,
the individual test cells must be isolated to eliminate shock loading from failure in adjacent test cells. Several
types of tensile creep test systems are shown in Fig. 9.
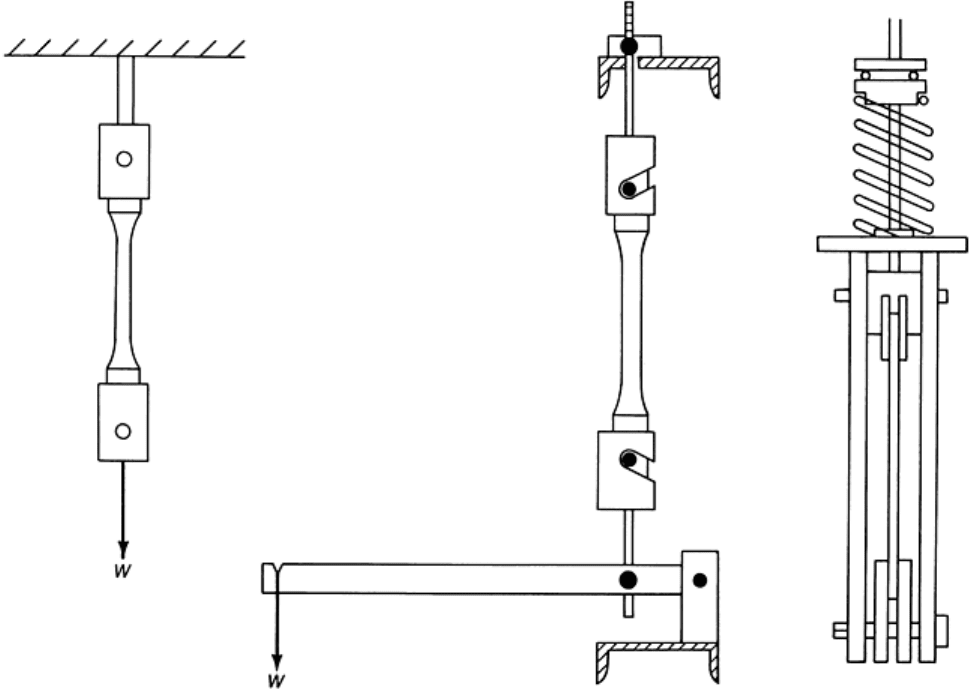
Fig. 9 Various equipment designs for the measurement of tensile creep in plastics
Creep curves generally exhibit three distinct phases. First-stage creep deformation is characterized by a rapid
deformation rate that decreases slowly to a constant value. The four-parameter model was proposed to describe
long-term creep. In this model, the first-stage creep deformation was called retarded elastic strain. Second-stage
creep deformation is characterized by a relative constant, low-deformation rate. In the four-parameter model,
this was called equilibrium viscous flow. The final or third-stage creep deformation is creep rupture, fracture, or
breakage.
The generalized uniaxial tensile creep behavior of plastics under constant load, isothermal temperature, and a
given environment can be illustrated as ductile creep behavior (Fig. 10a) or as brittle creep behavior (Fig. 10b).
At very low stress levels, both types of plastics exhibit similar first-stage and second-stage creep deformation.
The onset of creep rupture may not occur within the service life of the product (let alone the test). As the stress
level increases, first-stage and second-stage creep deformation rates remain relatively the same for these types,
but the time of failure is of course considerably reduced. In addition, third-stage creep deformation
characteristics now differ considerably. The ductile plastic exhibits typical ductile yielding or irreversible
plastic deformation prior to fracture. The brittle plastic, on the other hand, exhibits no observable gross plastic
deformation and only abrupt failure.
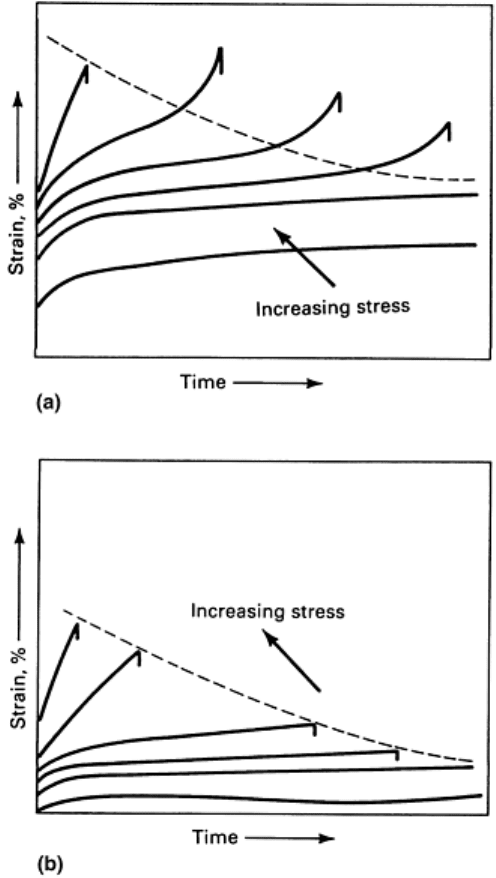
Fig. 10 Typical creep and creep rupture curves for polymers. (a) Ductile polymers. (b) Brittle polymers
Macroscopic yielding and fracture may not always be appropriate criteria for longtime duration material failure.
For some plastics, stress crazing, stress cracking, or stress whitening may signal product failure and may
therefore become a design limitation.
Creep strain is usually plotted against time on either semilog plots or log-log plots (Fig. 11). Extrapolation to
times beyond the data can be difficult on the semilog plot (Fig. 11a). Replotting on log-log paper may allow
easier extrapolation under one decade. Creep curves should not be extrapolated more than one decade, because
some curvature still remains in the log-log plot. For small strains, the curves can be considered linear. These
curves can usually be used to compare polymers at the same loading levels. Creep test data are also analyzed in
various forms, as described further in the section “Creep Data Analysis” in this article.
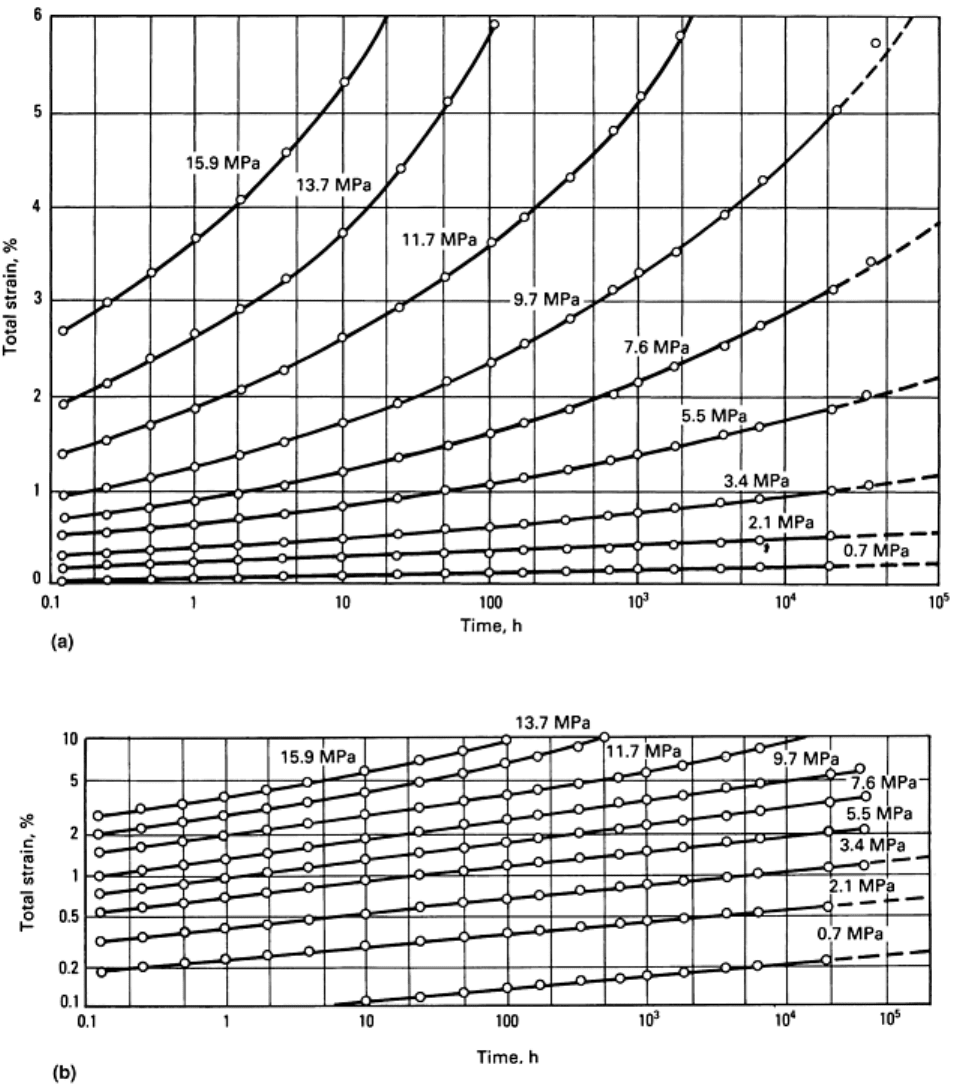
Fig. 11 Tensile creep strain of polypropylene copolymer. (a) Semilog plot. (b) Log-log plot
Other Strength/Modulus Tests
Compressive Strength Test (ASTM D 695 and ISO 604). Stress-strain properties are also measured for the
behavior of a material under a uniform compressive load. The procedure and nomenclature for compression
tests are similar to those for the tensile test. Universal testing machines can be used, and, like tension testing,
specimens should be preconditioned according to ASTM D 618 or ISO 291.
The standard test specimen in ASTM D 695 is a cylinder 12.7 mm (½ in.) in diameter and 25.4 mm (1 in.) in
height. The force of the compressive tool is increased by the downward thrust of the tool at a rate of 1.3
mm/min (0.05 in./min). The compressive strength is calculated by dividing the maximum compressive load by
the original cross section of the test specimen.
For plastics that do not fail by shattering fracture, the compressive strength is an arbitrary value and not a
fundamental property of the material tested. When there is no brittle failure, compressive strength is reported at

a particular deformation level such as 1 or 10%. Compressive strength of plastics may be useful in comparing
materials, but it is especially significant in the evaluation of cellular or foamed plastics. Compression testing of
cellular plastics is addressed in ISO Standards 1856 and 3386–1.
Typical compressive strengths for various plastics are compared in Fig. 12. Generally, the compressive
modulus and strength are higher than the corresponding tensile values for a given material.
Fig. 12 Compressive strength of engineering plastics. PA, polyamide; PET, polyethylene terephthalate;
PBT, polybutylene terephthalate; PPO, polyphenylene oxide; PC, polycarbonate; ABS, acrylonitrile-
butadiene-styrene
Compressive creep testing of plastic is addressed in ASTM D 2990. Normally creep information is given for
tension loading.
Flexural Strength Test (ASTM D 790 and ISO 178). Flexural strength or cross-breaking strength is the
maximum stress developed when a bar-shaped test piece, acting as a simple beam, is subjected to a bending
force. Two methods are used: three-point bending (Fig. 13) and four-point bending (Fig. 14). Four-point
bending is useful in testing materials that do not fail at the point of maximum stress in three-point bending (Ref
12).
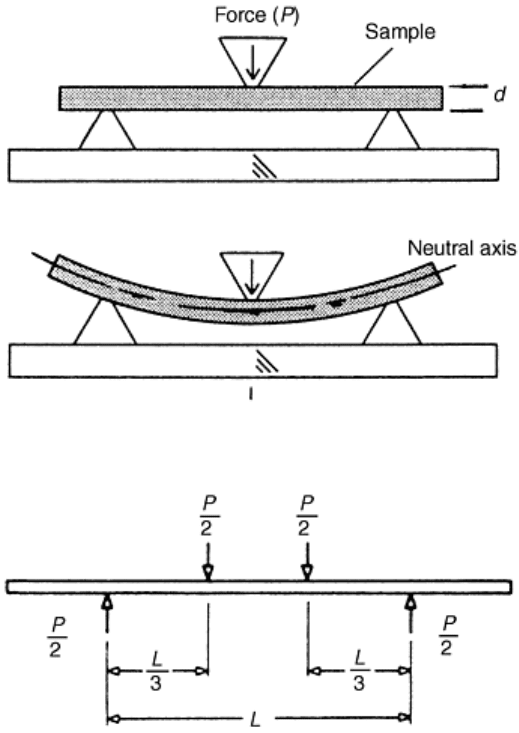
Fig. 13 Flexural test with three-point loading. Source: Ref 11
Fig. 14 Flexural test with four-point loading
For three-point bending, an acceptable test specimen is one at least 3.2 mm (0.125 in.) thick, 12.7 mm (0.5 in.)
wide, and long enough to overhang the supports (but with overhang less than 6.4 mm (0.25 in.) on each end).
The load should be applied at a specified crosshead rate, and the test should be terminated when the specimen
bends or is deflected by 0.05 mm/min (0.002 in./min). The flexural stress (S) at the outer fibers at mid-span in
three-point bending is calculated from the following expression:
S = 3PL/2bd
2
in which P is the force at a given point on the deflection curve, L is the support span, b is the width of the bar,
and d is the depth of the beam.
Because most plastics do not break from deflection, the flexural strength is measured when 5% strain occurs for
most thermoplastics and elastomers. Fracture strength under flexural load may be more suitable for thermosets.
To obtain the strain, r, of the specimen under three-point test, the following expression applies:
r = 6Dd/L
2
in which D is the deflection to obtain the maximum strain (r) of the specimen under test. To obtain data for
flexural modulus, which is a measure of stiffness, flexural stress is plotted versus strain, r, during the test; the
slope of the curve obtained is the flexural modulus. Flexural moduli for various plastics are compared in Fig.
15.
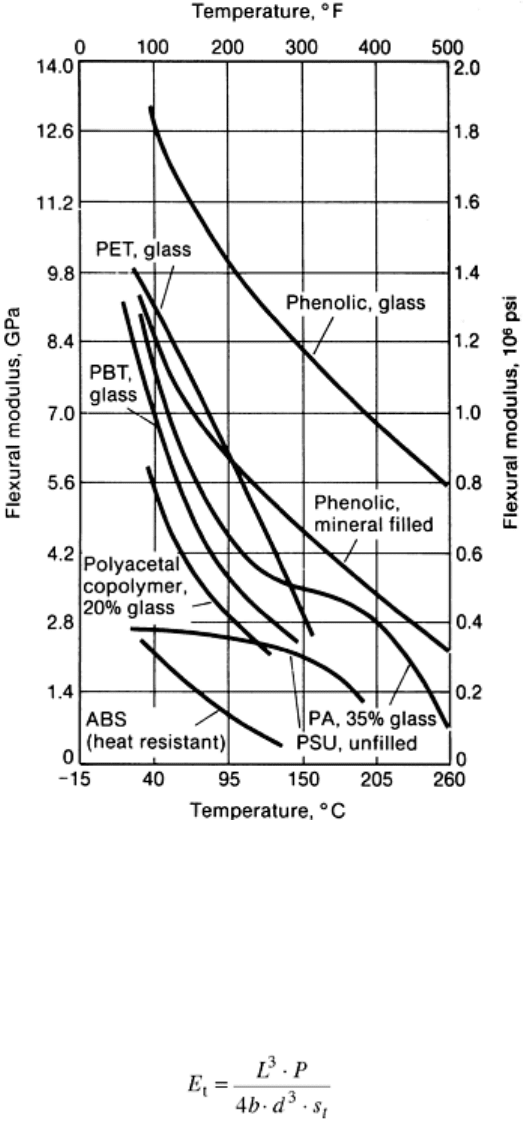
Fig. 15 Flexural modulus retention of engineering plastics at elevated temperatures. PET, polyethylene
terephthalate; PBT, polybutylene terephthalate; ABS, acrylonitrile-butadiene-styrene; PA, polyamide;
PSU, polysulfone
Flexural creep tests (ISO 899-2) are done with standard flexural test methods where the deflection is measured
as a function of time. The flexural creep modulus at time, t, (E
t
) for three-point bending (Fig. 13) is calculated
as:
where s
t
is the deflection at time, t.
Deflection Temperature under Load (ASTM D 648). Another measure of plastic rigidity under load is the
deflection temperature under load (DTUL) test, also known as the heat deflection temperature (HDT) test. In
the standard ASTM test (D 648), the heat deflection temperature is the temperature at which a 125 mm (5 in.)
bar deflects 0.25 mm (0.010 in.) when a load is placed in the center. It is typically reported at both 460 and
1820 kPa (65 and 265 psi) stresses. The specimen is placed in an oil bath under a load of 460 or 1820 kPa (65
or 265 psi) in the apparatus shown in Fig. 16, and the temperature is raised at a rate of 2 °C/min. The
temperature is recorded when the specimen deflects by 0.25 mm (0.01 in.). Because crystalline polymers, such
as nylon 6/6, have a low heat deflection temperature value when measured under a load of 1820 kPa (265 psi),
this test is often run at 460 kPa (65 psi).
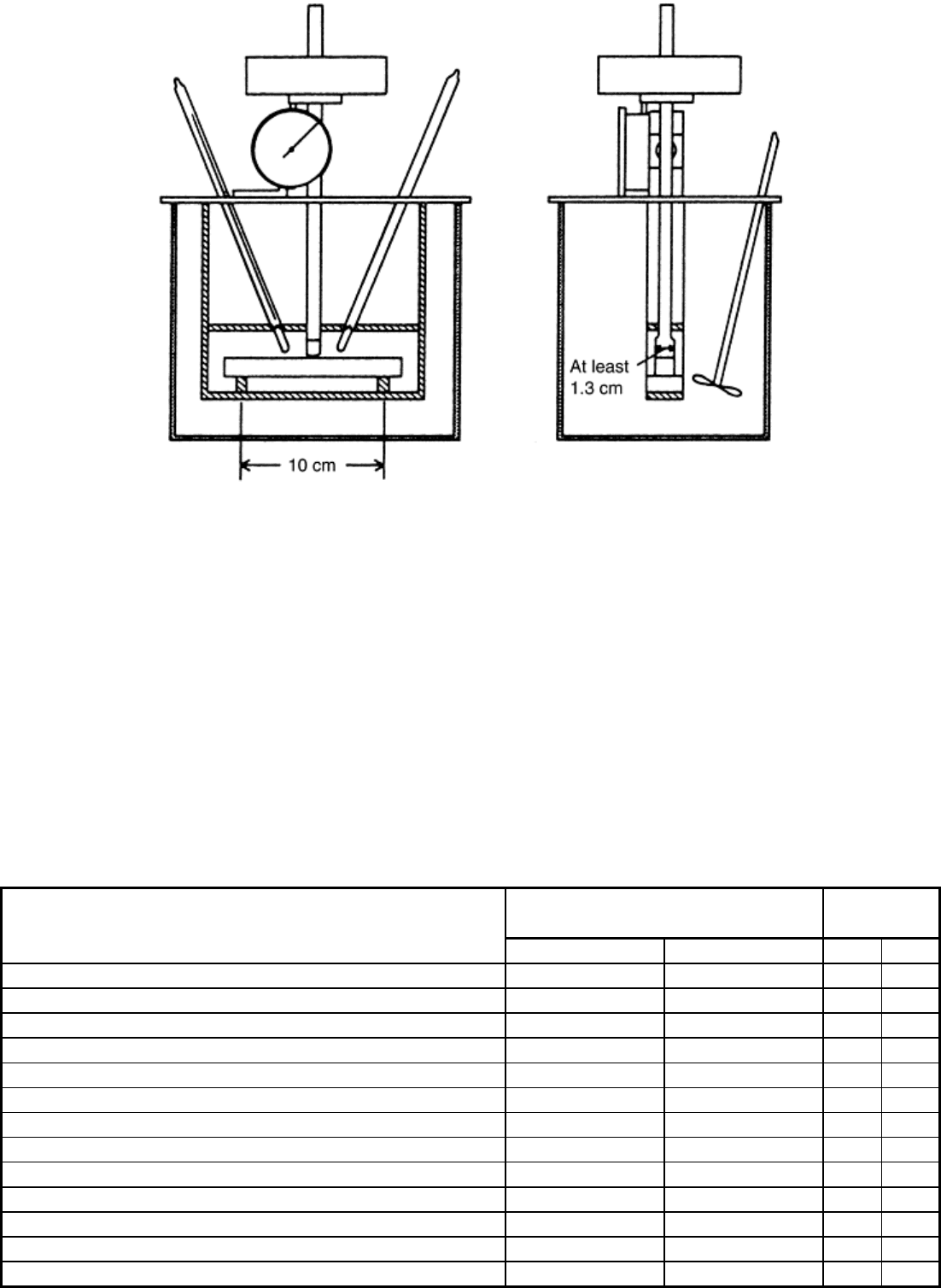
Fig. 16 Apparatus used in test for heat deflection temperature under load (460 or 1820 kPa, or 65 or 265
psi)
The heat deflection temperature is an often misused characteristic and must be used with caution. The
established deflection is extremely small, and in some instances may be, at least in part, a measure of warpage
or stress relief. The maximum resistance to continuous heat is an arbitrary value for useful temperatures, which
are always below the DTUL value. The DTUL value is also influenced by glass reinforcement.
The heat deflection temperature is more an indicator of general short-term temperature resistance. For long-
term temperature resistance, one of the most common measures is the thermal index determined by the
Underwriters' Laboratory (UL) (Ref 13). In this test, standard test specimens are exposed to different
temperatures and tested at varying intervals. Failure is said to occur when property values drop to 50% of their
initial value. The property criterion for determining the long-term use temperature depends on the application.
Table 8 lists typical HDT values and the UL temperature index for various plastics.
Table 8 Heat-deflection and Underwriters' Laboratories index temperatures for selected plastics
Heat-deflection temperature
at 1.82 MPa (0.264 ksi)
UL index
Material
°C °F °C
°F
Acrylonitrile-butadiene-styrene (ABS) 99 210 60
140
ABS-polycarbonate alloy (ABS-PC) 115 240 60
140
Diallyl phthalate (DAP) 285 545 130
265
Polyoxymethylene (POM) 136 275 85
185
Polymethyl methacrylate (PMMA) 92 200 90
195
Polyarylate (PAR) 155 310 …
…
Liquid crystal polymer (LCP) 311 590 220
430
Melamine-formaldehyde (MF) 183 360 130
265
Nylon 6 65 150 75
165
Nylon 6/6 90 195 75
165
Amorphous nylon 12 140 285 65
150
Polyarylether (PAE) 160 320 160
320
Polybutylene terephthalate (PBT) … … 120
250

Polycarbonate (PC) 129 265 115
240
PBT-PC 129 265 105
220
Polyetheretherketone (PEEK) … … 250
480
Polyether-imide (PEI) 210 410 170
340
Polyether sulfone (PESV) 203 395 170
340
Polyethylene terephthalate (PET) 224 435 140
285
Phenol-formaldehyde (PF) 163 325 150
300
Unsaturated polyester (UP) 279 535 130
265
Modified polyphenylene oxide alloy (PPO)(mod) 100 212 80
175
Polyphenylene sulfide (PPS) 260 500 200
390
Polysulfone (PSU) 174 345 140
285
Styrene-maleic anhydride terpolymer (SMA) 103 215 80 175
Shear Strength Test (ASTM D 732). The specimen proscribed in ASTM D 732 is a disc or a plate with an 11
mm ( in.) hole drilled through the center of the specimen. Testing can be done with a special fixture like the
one shown in Fig. 17. Shear strength is defined as the force for separation during loading divided by the area of
the sheared edge. Shear strength is often estimated as the tensile strength of a material. When a value for creep
shear modulus is needed, it is reasonable to divide the creep tensile modulus by 2.8.
Fig. 17 Example of set for shear-strength testing of plastics
Creep Data Analysis
Mechanical tests under tensile, compressive, flexural, and shear loading can be performed as either short-term
tests or long-term tests of creep deformation. Data for the long-term tests are typically recorded as time
dependent displacement values at various levels of constant stress (Fig. 18a). This type of data, however, can be
displayed and analyzed in several forms as shown in Fig. 18. There is no universal method of graphically
displaying tensile creep or, in fact, creep for compressive, shear, or flexural loading.
