ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

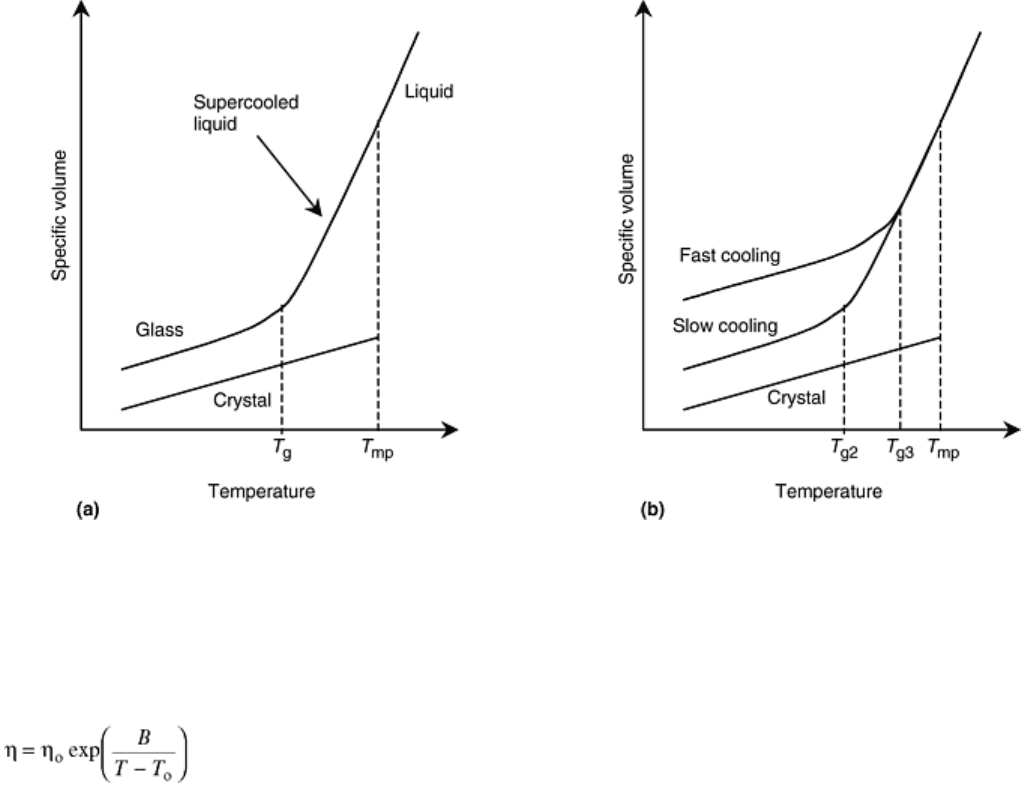
Fig. 11 Schematic representation of (a) the specific volume of liquid, glass, and crystal versus

temperature, and (b) the effect of cooling rate

The transition from supercooled liquid to glass during cooling is believed to be caused by a rapid rise in the

viscosity of the supercooled liquid during cooling. Empirical relationships have been derived to describe the

viscosity of glass as a function of temperature. The simplest relationship is (Ref 8):

(Eq 1)

where η is the viscosity, T is the absolute temperature, and η

B, and T

are constants.

Below the glass transition point, viscous flow of the supercooled liquid becomes so slow that the liquid begins

to behave as though it was elastic. In other words, the supercooled liquid structure existing at the glass

transition temperature becomes frozen in place below T

Most common inorganic glasses are based on the silicate tetrahedron shown in Fig. 12(a). A three-dimensional

solid forms when the corner oxygen atoms join with the adjacent tetrahedra. In the glassy state (Fig. 12b), the

tetrahedra join randomly, whereas in the crystalline state the tetrahedra take on long-range order, as illustrated

in Fig. 12(c). Pure silica glass exhibits a high glass transition temperature, making it suitable for elevated

temperature applications but also making it viscous and difficult to work. To overcome this problem, network

modifiers, such as CaO or Na

O, are usually added to commercial glasses. The network modifiers introduce

positive ions to the structure, which are accommodated by breaking up the three-dimensional network (Fig.

12d).

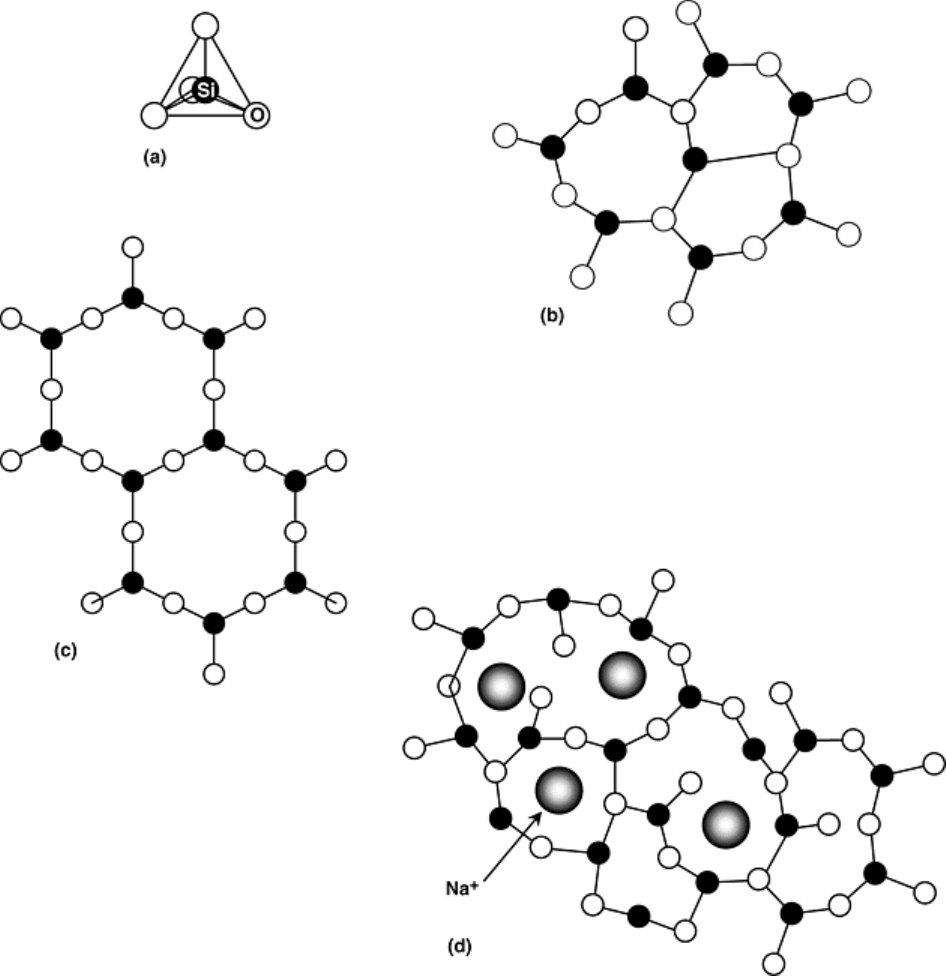
Fig. 12 Two-dimensional diagram of the structure of silica. (a) Silica tetrahedron. (b) In the form of

glass. (c) In the form of an ordered quartz crystal. (d) In the form of a Na

modified glass

Metallic glasses exhibit many unique physical and mechanical properties. Some of these materials exhibit high

strength coupled with high ductility, and high corrosion resistance. Metallic glasses deform by homogeneous

shear above their glass transition temperatures. In this type of flow, every atom or molecule responds to the

applied shear stress and participates in deformation. Homogeneous shear flow is a common deformation

mechanism in liquids. Above T

, metallic glasses behave like liquids. Below T

, the deformation is

inhomogeneous and occurs via the formation of localized shear bands. Each band is accompanied by extensive

local offsets. The formation of multiple shear bands can produce extensive ductility.

Polymers

As noted previously, polymers are composed of covalently bonded long-chain molecules, which are joined

together by secondary bonds or covalent cross links. Under applied stresses, polymer chains slide over each

other, and failure occurs by separation of chains rather than by breaking of interchain bonds. This type of

motion is relatively easy where secondary bonds join molecules. However, most polymers have side branches

or bulky side groups on their chains and are not strictly linear. Side branches alter the properties of polymers by

inhibiting interchain sliding. Cross-linking also influences the properties of polymers. Cross-linking can occur,

for example, when unsaturated carbon bonds (e.g., double bonds) exist between the atoms making up the

backbone of the polymer chain that can be broken, allowing individual atoms or molecules to link to adjacent

chains. Heavily cross-linked polymers can develop rigid three-dimensional network structures that inhibit

interchain sliding, resulting in increased strength and decreased ductility.

Structurally, most polymers are amorphous and consist of a random arrangement of molecules, as illustrated in

Fig. 13. Examples of amorphous polymers include polyvinyl chloride (PVC), polymethyl methacrylate

(PMMA), and polycarbonate (PC).

Fig. 13 Schematic representation of a polymer. The spheres represent the repeating units of the polymer

chain, not individual atoms. Source: Ref 9

Some polymers can exhibit limited crystallinity. This occurs when the polymer chains arrange themselves in a

regular manner. Crystalline polymers are characterized by a degree of crystallinity, which is a measure of the

extent of long-range three-dimensional order. In general, simple polymers, such as polyethylene with little or no

side branching crystallize very easily whereas in heavily cross-linked polymers, such as polyisoprene, and in

polymers containing bulky side groups, crystallization is inhibited. As such, thermoset polymers are seldom

crystalline. In polymers containing side groups, the degree of crystallinity is often to the location of the side

group. Polystyrene (PS), for example, is amorphous in its atactic form where benzene ring substitution is

random within each repeating unit of the molecule. However, PS is crystalline in the isotactic form where

substitution occurs at the same location within each repeating unit. The regular structure of the isotactic form

promotes crystallinity. Crystalline structures are also likely in polymers that are syndyotactic, where the side

groups alternate positions in a regular manner. Examples of atactic, isotactic, and syndiotactic arrangements are

schematically illustrated in 14 14Fig. 14.

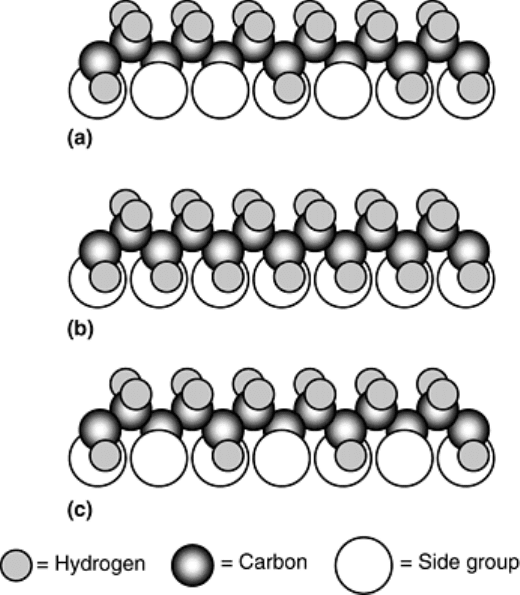
Fig. 14 Schematic representation of the possible side group arrangements in a simple vinyl polymer: (a)

atactic (random), (b) isotactic (all on same side), and (c) syndiotactic (regularly alternating). Source: Ref

Amorphous polymers are normally used near or below their glass transition temperatures. Above this

temperature, the elastic modulus decreases rapidly, and creep effects become pronounced. Below this

temperature, they tend to be glassy and brittle with elastic moduli on the order of 3 GPa. Crystalline polymers

are, in general, less brittle than amorphous polymers. In addition, they retain their strength and stiffness more

effectively than amorphous polymers at elevated temperatures.

Some polymers, known as network polymers or cross-linked thermosets, form three-dimensional structures via

cross-linking between chains. Common examples include Bakelite, polyester resins, and epoxy adhesives. In

Bakelite, cross-links form by means of phenol rings, which are integral parts of each chain. The structure of

Bakelite is schematically illustrated in Fig. 15. Unlike thermoplastic polymers, thermosets do not have real

glass-transition temperatures and thus will not melt during heating. Instead, they tend to degrade

(depolymerize) at elevated temperatures.

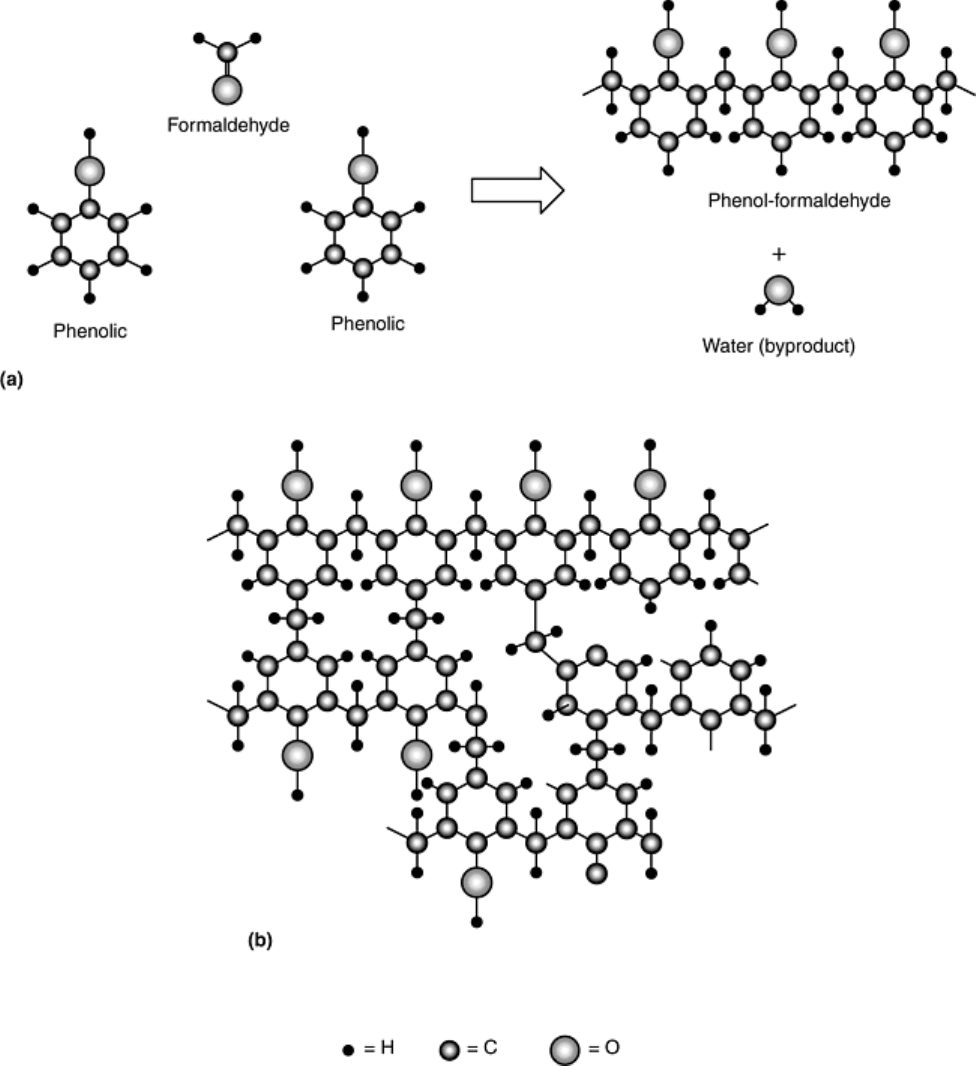
Fig. 15 Schematic representation of the structure of a phenol formaldehyde. (a) Two phenol rings join

with a formaldehyde molecule to form a linear chain polymer and molecular by-product. (b) Excess

formaldehyde results in the formation of a network, thermosetting polymer due to cross-linking.

Elastomers are another class of polymers that include natural rubber and a variety of other synthetic polymers

exhibiting similar mechanical properties. Elastomers also form via cross linking between chains, and most

behave like thermosets. Polyisoprene, for example, is a synthetic polymer with the same basic structure as

natural rubber, but without the impurities found in natural rubber. The addition of sulfur along with heat (~140

°C) and pressure causes sulfur cross-links to form. As the degree of cross-linking increases, the polymer

becomes harder. This particular process is known as vulcanization. A schematic representation of these cross-

linking arrangements is shown in Fig. 16. Sometimes curved polymer chains can also evolve due to the

arrangement of bonds between the atoms forming the backbone of each chain. This is schematically represented

in Fig. 17. In this example, the molecule or atom, R, is placed on an unsaturated carbon chain in either a cis or

trans position. In the cis position, the unsaturated bonds lie on the same side of the chain. In the trans position,

they lie on opposite sides of the chain. The cis structure makes the molecule tend to coil rather than remain

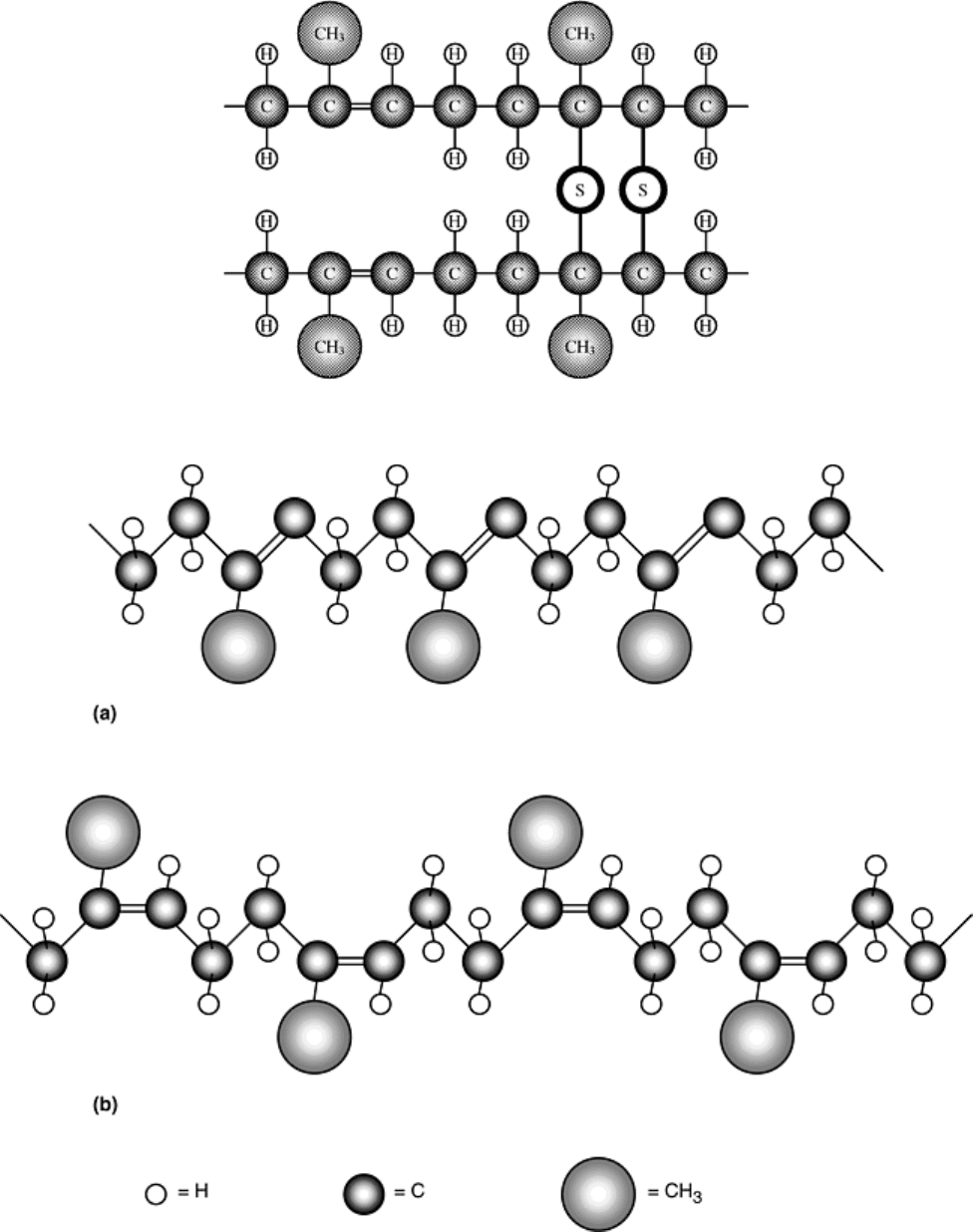
linear. This coiling is believed to be responsible for the extensive elasticity observed in elastomers (e.g.,

rubber).

Fig. 16 Schematic representation of cross-linking in polyisoprene

Fig. 17 Schematic representation of (a) cis and (b) trans structures in polyisoprene

References cited in this section

6. H. Baker, Structure and Properties of Metals, Metals Handbook Desk Edition, 2nd ed., ASM

International, 1998, p 85–121

7. R.E. Reed-Hill and R. Abbaschian, Physical Metallurgy Principles, 3rd ed., PWS-Kent, Boston, 1992

8. R.H. Doremus, Glass Science, 2nd ed., John Wiley & Sons, 1994, p 109

9. W.G. Moffatt, G.W. Pearsall, and J. Wulff, Structure, Vol 1, The Structure and Properties of Materials,

John Wiley & Sons, 1964, p 104

10. W.G. Moffatt, G.W. Pearsall, and J. Wulff, Structure, Vol 1, The Structure and Properties of Materials,

John Wiley & Sons, 1964, p 106

Introduction to the Mechanical Behavior of Nonmetallic Materials

M.L. Weaver and M.E. Stevenson, The University of Alabama, Tuscaloosa

Deformation/Strengthening Mechanisms

Crystalline Solids

As noted in the previous article, metals generally deform via slip and/or twinning. Slip occurs via the motion of

dislocations on close-packed planes and in close-packed directions, whereas twinning occurs via the

cooperative movement of atoms producing a macroscopic shear. In slip, the combination of slip planes and

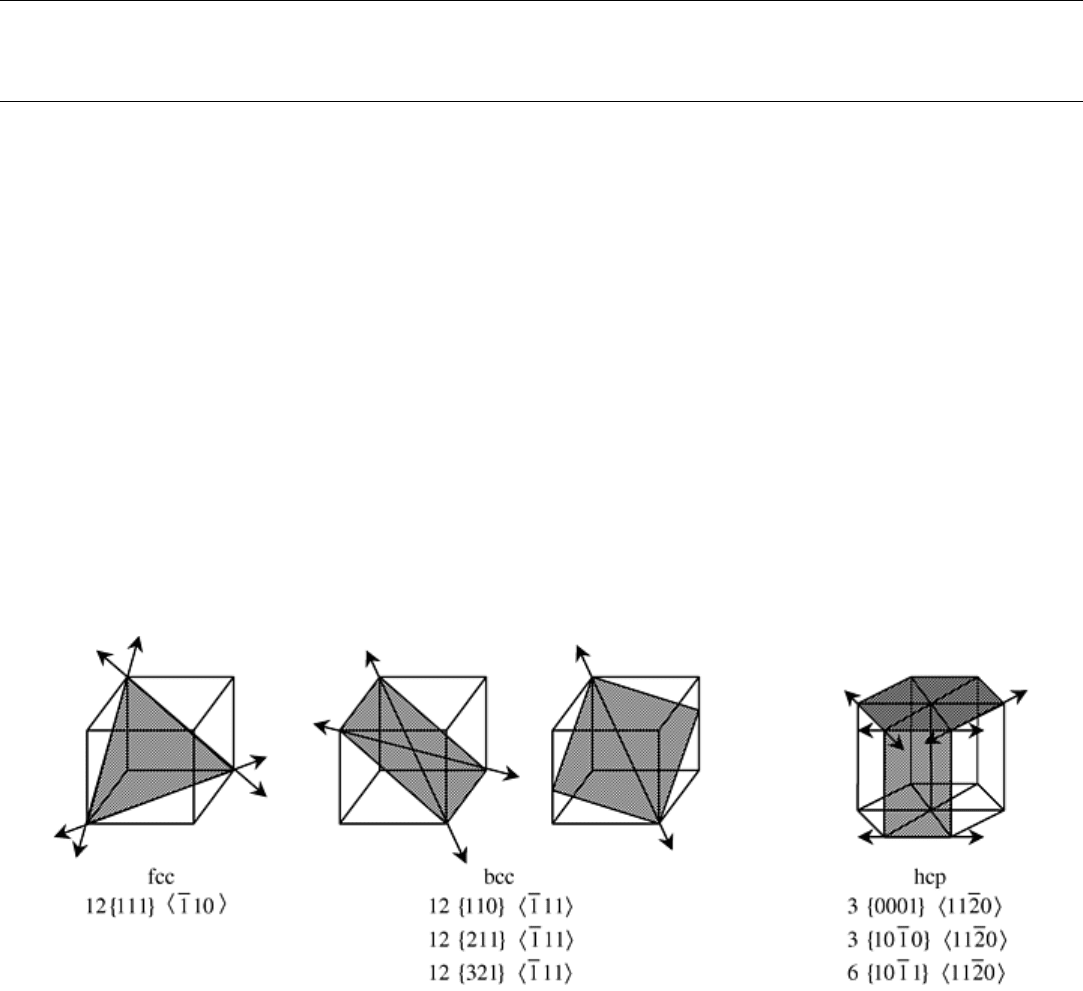
directions are known as slip systems. The most common slip systems for disordered metals and alloys are

schematically illustrated in Fig. 18. According to the von Mises criteria, at least five independent slip systems

must be available in polycrystalline materials for the material to be capable of plastic deformation. Thus, the

greater the number of independent slip systems, the greater is the possibility for plastic deformation. Most

technically significant metals and alloys with cubic structures have five or more independent slip systems and

thus exhibit substantial plasticity. For example, Ni and Cu, which are fcc metals, each have five independent

slip systems and are extremely ductile at ambient temperatures. However, Co, which is an hcp metal, has less

than five independent slip systems and is brittle at ambient temperatures. Metals with less than five slip systems

can exhibit plasticity at ambient temperatures provided other deformation modes are available. A good example

of this is Zn, which exhibits only three systems but also exhibits twinning.

Fig. 18 Common slip systems observed for fcc, bcc, and hcp crystal structures

Twinning is a particularly important deformation mode in materials where slip is restricted. A schematic

diagram of twinning is provided in Fig. 19. Twinning produces a reorientation of the lattice resulting in a region

that is a mirror image of the parent lattice. The actual amount of strain that is gained from twinning is very

small (typically less than 5%). The true benefit of twinning is that the lattice inside the twin is frequently

reoriented such that the slip systems are more favorably aligned with respect to the applied stress, which can

allow some limited plastic deformation to occur.

Fig. 19 Schematic of twinning as it occurs in an fcc lattice. Source: Ref 11

Plastic deformation in ceramic and intermetallics also occurs via slip and/or twinning. However, plastic

deformation is typically more difficult in ceramics and intermetallics compared with metals, due, in part, to the

strong and directional atomic bonds, ordered atomic distributions, and less symmetric lattice structures present

in these materials. These features combine to restrict the motion of dislocations. In comparison with metals,

ceramics are considered to be intrinsically hard and brittle. Intermetallics cannot be described as being

intrinsically hard or soft; however, they are typically brittle. The different mechanical properties of these

materials are related to bonding. The metallic bonds in metals make dislocation motion relatively easy, whereas

the highly directional ionic, covalent, and mixed bonds observed in ceramics and intermetallics present large

lattice resistance to dislocation motion.

In their polycrystalline form, most ceramics and intermetallics exhibit limited plasticity at ambient temperatures

because they do not have enough independent slip systems for general deformation to occur. In many of these

materials the lack of slip systems can be traced to the crystal structure, which is often so complex that the stress

required to move a dislocation (the Peierls stress) becomes larger than the fracture stress. In NaCl, for example,

slip occurs on {111} 〈1 0〉 slip systems at ambient temperatures. This only yields two independent slip

systems, which is not enough for polycrystalline ductility. In isostructural AgCl, slip occurs on both {111} and

{100} planes, which provide enough independent slip systems for polycrystalline deformation.

In ionically bonded polycrystalline ceramics such as NaCl, deformation is further complicated because local

charge neutrality must be maintained during deformation. In ionic ceramics, proper charge balance on either

side of the slip plane is accomplished by introducing two extra half planes of atoms. The lines of ions at the

bottoms of these half planes consist of alternating positive and negative ions. Dislocations can become charged,

which can influence their mobility. The formation of a jog in a dislocation ( 20) can cause a localized charge

imbalance, which must be compensated for by the formation of defects of the accumulation of atmospheres of

oppositely charged impurities.

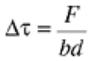
Fig. 20 (a) Schematic representation of an edge dislocation in NaCl. (b) Demonstration of how

dislocation jogs in ionic crystals can have effective charges. Source: Ref 12

In more covalent ceramics and intermetallics, slip is complicated by the requirement that atomic order must be

maintained. Perfect single dislocations, which do not influence the order of atoms, have longer Burgers vectors

than dislocations in disordered alloys. Thus, these dislocations have higher strain energy. Such dislocations can

assume lower energy configurations by dissociating into shorter dislocation segments, partial dislocations,

which are separated by stacking faults an/or antiphase boundaries. These combinations of partial dislocations,

stacking faults, and antiphase boundaries are known as superdislocations. When superdislocations move, the

atomic order that is destroyed by passage of the leading partial dislocation is restored by passage of the trailing

partial dislocation. Additional reasons for the lack of ductility in intermetallics include: difficulty transmitting

slip across grain boundaries, intrinsic grain boundary weakness, segregation of deleterious solutes to grain

boundaries, covalent bonding and high Peierls stress, and environmental susceptibility. Increased ductility can

be obtained in some intermetallics by microalloying (e.g., NiAl with Fe, Mo, or Ga; Ni

Al with B; or Ti

with Nb). At higher temperatures, however, thermal activation permits additional slip activity to occur in all of

these materials, which may allow them to be ductile.

Strengthening Mechanisms in Crystalline Solids (Ref 13, 14, 15)

As just discussed, ceramics and intermetallics generally deform via slip and/or twinning. As a result, anything

that reduces the mobility of dislocations (i.e., anything that inhibits slip) will cause an increase in strength. The

most common strengthening mechanisms, work hardening, solid-solution hardening, particle/precipitation

hardening, and grain size hardening are described here.

Solid Solution Strengthening. Pure metals generally have low yield stresses compared with impure metals or

single-phase alloys and compounds. The addition of substitutional or interstitial solute atoms to the lattice of a

pure metal gives rise to local stress fields around each impurity atom. These local stress fields interact with

those surrounding dislocations, which reduces the mobility of dislocations leading to increased strength. The

amount of strengthening is related to the binding energy between the solute atoms and the dislocation, the

concentration of the solute atoms, and the locations of the solute atoms within the lattice. For example, the

magnitude of strengthening can be greater when solute atoms assume specific locations within the lattice (i.e.,

they order) as opposed to when they assume random positions. The same general principles apply in ceramics

and intermetallics; however, the presence of long-range ordered crystal structures and charged ions within these

materials makes it difficult to apply conventional models for solid solution hardening.

Solid solution strengthening can be considered by assuming that each foreign atom produces a restraining force,

F, on the dislocation line. The magnitude of the restraining force (and thus the amount of strengthening

obtained) depends on the nature of the interactions between foreign atoms and dislocations. The two most

common interactions are elastic interactions and chemical interactions. Assuming that the atoms are spaced at

an average distance, d, along the dislocation line, and that the dislocation glides a distance b on the slip plane,

the ratio F/d gives the force per unit length of dislocation that must be overcome by the applied shear stress, τ.

The increment in applied stress needed to overcome the restraining force per unit line length is Δτb such that:

(Eq 2)

When the solute atoms have different sizes than the host atoms or different elastic moduli, they tend to alter the

crystal lattice locally in the vicinity of the solute atom. This causes the moving dislocation to be either attracted

to or repelled away from the solute. When the dislocation is attracted toward the solute, strengthening is caused

because more force is required to pull the dislocation away from the solute. When the dislocation is repelled by

the solute, strengthening is caused because more force is required to push the dislocation past the solute atom.

Solid solution strengthening can occur in ceramics and intermetallics just as it does in metals. Both

substitutional and interstitial types are possible. In ceramics, interstitial solid-solution strengthening will occur

if the ionic radius of the solute is small in comparison with the solvent (anion). In the case of substitutional

solid-solution strengthening, because both anions and cations are present, a substitutional impurity will

substitute for the host ion to which it is most similar in the electrical sense (i.e., if the impurity atom normally

forms a cation in a ceramic material, then it will likely substitute for the host cation). In NaCl, for example,

and O

would probably substitute for Na

and Cl

ions, respectively. To achieve appreciable solid

solubility, the ionic size and charge of the substituting atoms must be nearly the same as those of the host ions.

If impurity ions have different charges than the host ions, the crystal must compensate structurally such that

charge neutrality is maintained. This can be accomplished by the formation of lattice defects, such as vacancies

or interstitials (Schottky, Frenkel defects).

In ionic crystals, the presence of charged dislocations also plays a role. Solutes exhibiting different valence than

the host atoms (i.e., aliovalent) are more effective in increasing the yield stress than ions with the same valence

(isovalent). Aliovalent ions are more effective because they produce an asymmetric elastic distortion, which

interacts strongly with dislocations. The stress increment caused by solid solution strengthening in ceramics is

described by the equation:

(Eq 3)

where T is the absolute temperature, T

= GΔεb

/(3.86αk), τ

= GΔεc

1/2

/(3.3), c is the concentration of defects,

Δε is the misfit strain, b is the Burgers vector, α is a constant, and k is Boltzmann's constant (Ref 14).

Work hardening, also known as strain hardening, is an important industrial process that is used to harden metals

or alloys. The hardening or strengthening is a direct result of dislocation multiplication and dislocation-

dislocation interactions. Work hardening is also an important phenomenon in some intermetallic systems but is

not a viable process for ceramics and glasses. Polymers do not work harden; however, an analogous

phenomenon, cold drawing, occurs in thermoplastics. Cold drawing is addressed in a subsequent section of this

article.

When dislocations moving on intersecting slip systems collide some of them will become pinned. The more the

material is plastically deformed, the higher the dislocation density becomes, resulting in more restricted

dislocation motion. A high work hardening rate implies the obstruction of dislocations gliding on intersecting

systems. Thus, techniques that increase dislocation density also increase strength. For a given dislocation

distribution, the shear flow stress, τ, is related to the dislocation density, ρ, by an equation of the form:

τ = τ

+ αGbρ

1/2

(Eq 4)

where α is a materials specific constant that varies from 0.2 to 0.4 for different fcc and bcc metals, G is the

material shear modulus, b is the Burgers vector, and τ

is the flow strength in absence of work hardening (Ref

6). At high strains, dislocations will tangle and form cell structures. The hardening then becomes more a

function of cell size than of dislocation length.

Grain Size Strengthening. Internal boundaries also act as obstacles to dislocation motion. Boundaries impede

dislocations over a large length, which often makes boundary strengthening a more potent strengthening

mechanism than solid-solution strengthening or work hardening. At grain boundaries, there is a change in

crystallographic orientation, which prevents or inhibits the passage of dislocations. For slip to continue across a

grain boundary, yielding must occur within the adjacent grain. If the orientation of the adjacent grain is

unfavorable, dislocations will pile up against the boundary leading to a stress concentration at the boundary.

Under action of a stress concentration, slip can be initiated within the adjacent grain. The increase in stress

associated with grain size can be represented by the Hall-Petch relation from which the stress increment can be

written as:

(Eq 5)

where D is the grain diameter and k

is a locking parameter that describes the relative strength of the boundary.

This relationship shows that as the grain size increases, the stress concentration at the boundary decreases,

resulting in reduced strengthening compared with fine-grained materials. Other boundaries such as subgrain

boundaries and stacking faults can also form obstacles to dislocation motion; however, they are less potent

strengtheners than grain boundaries.

Precipitation/Particle Hardening. Substantial strengthening can also be obtained by adding precipitates or

dispersoids to the material. The extent of strengthening is determined by a number of factors including volume

fraction, particle size, particle shape, and strength of the particle-matrix interface (Ref 14, 15). This is directly

related to interactions between moving dislocations and the particles as the presence of particles inhibits

dislocations by providing additional barriers to their motion.