ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

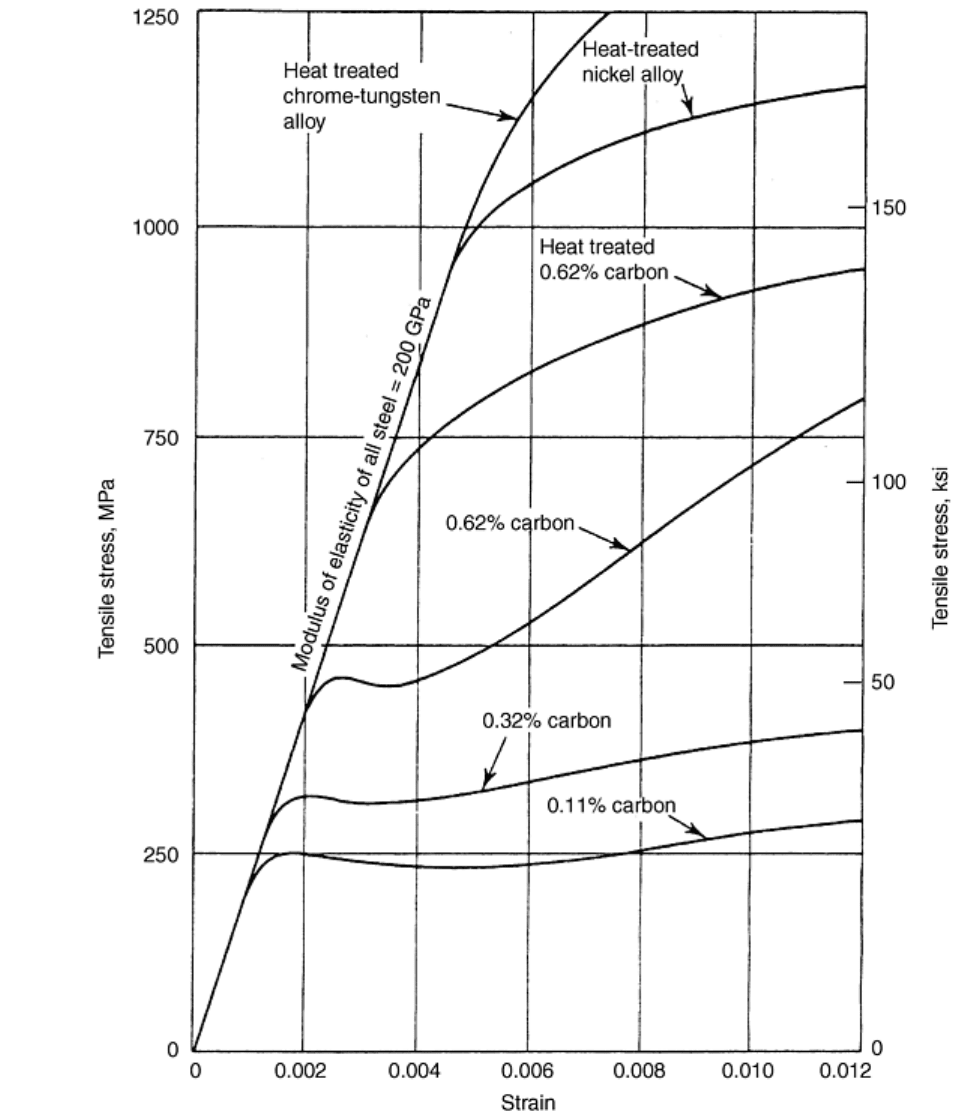
Fig. 3 Stress-strain diagram for various steels. Source: Ref 8

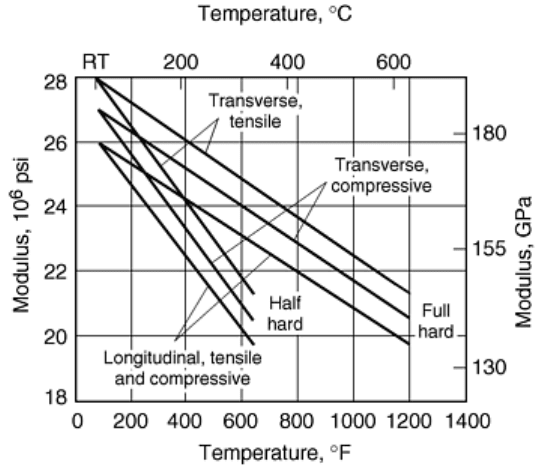
Fig. 4 Tensile and compressive modulus at half-hard and full-hard type 301 stainless steel in the

transverse and longitudinal directions. Source: Ref 5

Equations 1 and 5 can be combined with Eq 4 to give the design equation:

ΔL = FL/AE < δ

(Eq 6)

where δ is the design limit on change in length of the bar. Just as the strength, or load-carrying capacity, of the

tie bar is related to geometry and material strength (Eq 2), the stiffness of the bar is related to geometry and the

elastic modulus of the material. Again, part performance (force, F, and deflection, δ) is combined with part

geometry (length, L, and cross-sectional area, A) and material characteristics (elastic modulus, E) in this design

equation. To assure that the change in length is less than the allowable limit for a given force and material, the

geometry parameters L and A can be calculated; or, for given dimensions, the maximum load can be calculated.

Alternatively, for a given force and geometric parameters, materials can be selected whose elastic modulus, E,

meets the design criterion given in Eq 6.

Similar to design for strength, additional criteria involving minimum weight or cost can be incorporated into

design for stiffness. These criteria lead to the material selection parameters modulus-to-weight ratio (E/ρ) and

modulus-to-cost ratio (E/ρc), values that can be found in Ref 7 and ASM Handbook, Volume 20.

Mechanical Testing for Stress at Failure and Elastic Modulus. In Eq 2 and 6, the material properties σ

and E

play critical roles in design of the tie bar. These properties are determined from a simple tension test described

in detail in the article “Uniaxial Tension Testing” in this Volume. The elastic modulus E is determined from the

slope of the elastic part of the tensile stress strain curve, and the failure stress, σ

, is determined from the tensile

yield strength, σ

, or the ultimate tensile strength, σ

Tension-test specimens are cut from representative samples, as described in more detail in the article “Uniaxial

Tension Testing.” in the example of the tie bar, test pieces would be cut from bar stock that has been processed

similarly to the tie bar to be used in the product. In addition, the test piece should be machined such that its

gage length is parallel to the axis of the bar. This ensures that any anisotropy of the microstructural features will

affect performance of the tie bar in the same way that they influence the measurements in the tension test. For

example, test pieces cut longitudinally and transverse to the rolling direction of hot rolled steel plates will

exhibit the same elastic modulus and yield strength, but the tensile strength and ductility will be lower in the

transverse direction because the stresses will be perpendicular to the alignment of inclusions caused by hot

rolling (Ref 10).

During tension testing of a material to measure E and σ

, in addition to the change in length due to the applied

axial tensile loads, the material will undergo a decrease in diameter. This reflects another elastic property of

materials, the Poisson ratio, given by:

ν = -ε

/ε

(Eq 7)

where ε

is the transverse strain and ε

is the longitudinal strain measured during the elastic part of the tension

test. Typical values of ν range from 0.25 to 0.40 for most structural materials, but ν approaches zero for

structural foams and approaches 0.5 for materials undergoing plastic deformation. While the Poisson effect is of

no consequence in the overall behavior of the tie bar (since the decrease in diameter has a negligible effect on

the stress in the bar), the Poisson ratio is a very important material parameter in parts subjected to multiple

stresses. The stress in one direction affects the stress in another direction via ν. Therefore, accurate

measurements of the Poisson ratio are essential for reliable design analyses of the complex stresses in actual

part geometries, as described later. Typical values of Poisson's ratio are given in Table 4.

Sonic methods also offer an alternative and more accurate measurement of elastic properties, because the

velocity of an extensional sound wave (i.e., longitudinal wave speed, V

) is directly related to the square root of

the ratio of elastic modulus and density as follows:

= (E/ρ)

1/2

(Eq 8)

By striking a sample of material on one end and measuring the time for the pulse to travel to the other end, the

velocity can be calculated. Combining this with independent measurement of the density, Eq 8 can be used to

calculate the elastic modulus (Ref 8).

References cited in this section

3. Metals Handbook, American Society for Metals, 1948

4. F.B. Seely, Resistance of Materials, John Wiley & Sons, 1947

5. Properties and Selection of Metals, Vol 1, Metals Handbook, 8th ed., American Society for Metals,

1961, p 503

6. Modern Plastics Encyclopedia, McGraw Hill, 2000

7. M.F. Ashby, Materials Selection for Mechanical Design, 2nd ed., Butterworth-Heinemann, 1999

8. H. Davis, G. Troxell, and G. Hauck, The Testing of Engineering Materials, 4th ed., McGraw Hill, 1982,

p 314

9. G. Carter, Principles of Physical and Chemical Metallurgy, American Society for Metals, 1979, p 87

10. M.A. Meyers and K.K. Chawla, Mechanical Metallurgy, Prentice-Hall, Edgewood Cliffs, NJ, 1984, p

626–627

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Compressive Loading

If the bar in Fig. 1 were subjected to a compressive axial load, the same design criteria, Eq 2 and 7, would apply

with appropriate material parameters. Measurement of the material parameters could be performed through

compression tests; however, in anisotropic materials, the yield strength, σ

, will be the same in compression and

tension. The material ultimate strength, σ

, will generally be different, however, because the fracture behavior

of a material in compression is different from that in tension. Tests for failure in compression are covered in the

article “Uniaxial Compression Testing” in this volume. In carrying out compression tests, the same precautions

used in tension testing must be applied regarding orientation of the specimen and load relative to the material

microstructure.

In compressive loading of materials, buckling may precede other forms of failure, particularly in long thin bars.

The critical compressive stress for buckling of bars with simple pin-end supports is given by:

= F/A = π

EI/L

(Eq 9)

where I is the moment of inertia of the bar cross section. The only material parameter in Eq 9 is the elastic

modulus, which is the same in tension and compression for most materials. Any convenient test for E, then, can

be used to provide the material parameter required for buckling predictions.

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Hardness Testing

When suitable samples for tension or compression test pieces are too difficult, costly, or time consuming to

obtain, hardness testing can be a useful way to estimate the mechanical strength and characteristics of some

materials. Hardness testing, therefore, is an indispensable tool for evaluating materials and estimating other

mechanical properties from hardness (Ref 11, 12).

Correlation of hardness and strength has been examined for several materials as summarized in Ref 12. In

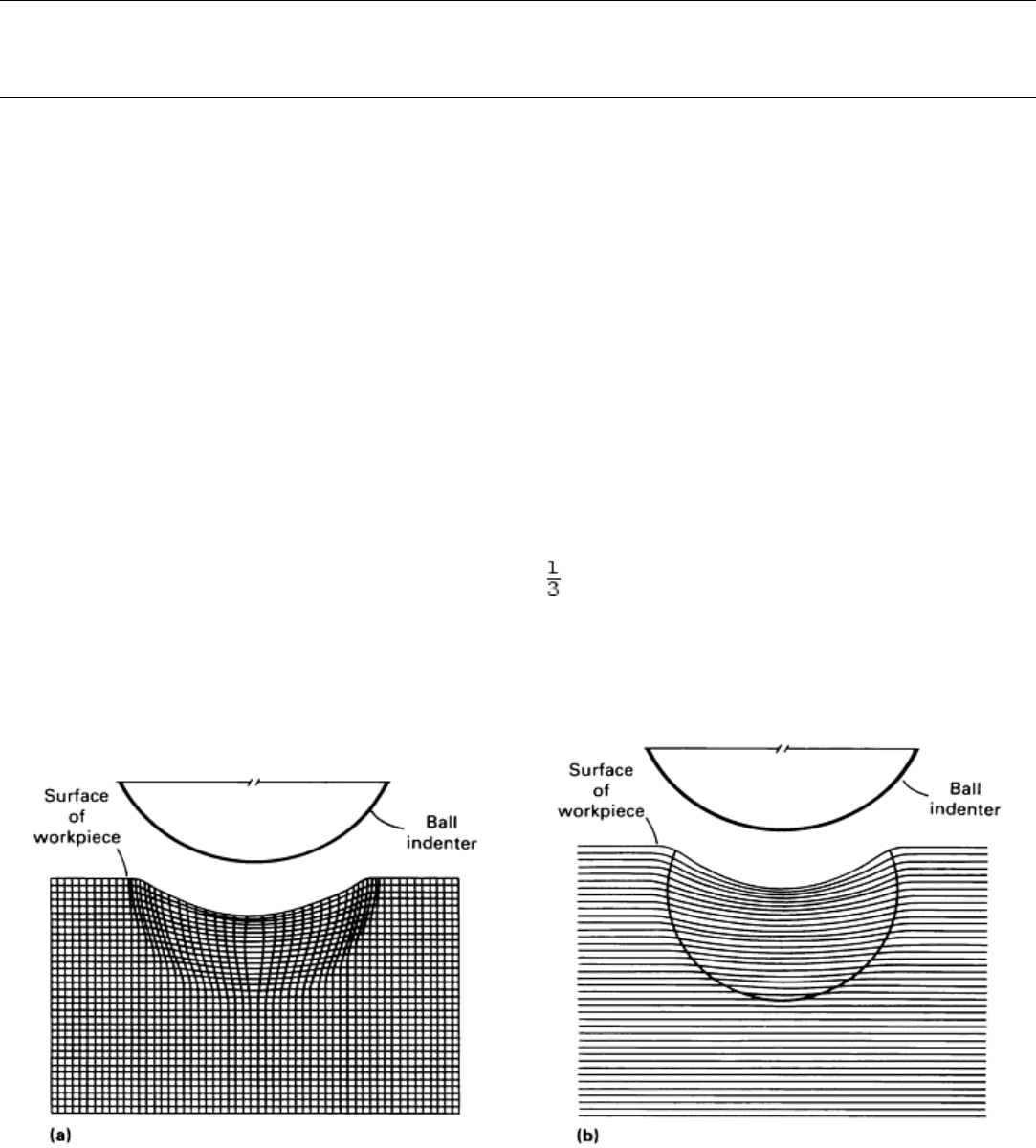
hardness testing, a simple flat, spherical, or diamond-shaped indenter is forced under load into the surface of the

material to be tested, causing plastic flow of material beneath the indenter as illustrated in Fig. 5. It would be

expected, then, that the resistance to indentation or hardness is proportional to the yield strength of the material.

Plasticity analysis (Ref 13) and empirical evidence (summarized in Ref 12) show that the pressure on the

indenter is approximately three times the tensile yield strength of the material. However, correlation of hardness

and yield strength is only straightforward when the strain-hardening coefficient varies directly with hardness.

For carbon steels, the following relation has been developed to relate yield strength (YS) to Vickers hardness

(HV) data (Ref 12):

YS (in kgf/mm

) = HV (0.1)

m-2

where m is Meyer's strain-hardening coefficient (see the article “Introduction to Hardness Testing” in this

Volume). To convert kgf/mm

values to units of lbf/in.

, multiply the former by 1422. This relation applies only

to carbon steels. Correlation of yield strength and hardness depends on the strengthening mechanism of the

material. With aluminum alloys, for example, aged alloys exhibit higher strain-hardening coefficients and lower

yield strengths than cold worked alloys (Ref 12).

Fig. 5 Deformation beneath a hardness indenter. (a) Modeling clay. (b) Low-carbon steel

For many metals and alloys, there has been found to be a reasonably accurate correlation between hardness and

tensile strength, σ

(Ref 12). Several studies are cited and described in Ref 12, and Tables 5 and 6 summarize

hardness-tensile strength multiplying factors for various materials. It must be emphasized, however, that these

are empirically based relationships, and so testing may still be warranted to confirm a correlation of tensile

strength and hardness for a particular material (and/or material condition). A correlation with hardness may not

be evident. For example, magnesium alloy castings did not exhibit a hardness-strength correlation in a study by

Taylor (Ref 11).

Table 5 Hardness-tensile strength conversions for steel

Material

Multiplying factor

(a)

Heat-treated alloy steel (250–400 HB)

470 HB

Heat-treated carbon and alloy steel (<250 HB)

482 HB

Medium carbon steel (as-rolled, normalized, or annealed)

493 HB

(a) Tensile strength (in psi) = multiplying factor × HB.

Source: Ref 12

Table 6 Multiplying factors for obtaining tensile strength from hardness

Material

Multiplying factor range

(a)

Heat treated carbon and alloy steel

470–515 HB

Annealed carbon steel

515–560 HB

All steels

448–515 HV

Ni-Cr austenitic steels

448–482 HV

Steel; sheet, strip, and tube

414–538 HV

Aluminum alloys; bar and extrusions

426–650 HB

Aluminum alloys; bar and extrusions

414–605 HV

Aluminum alloys; sheet, strip, and tube

470–582 HV

Al-Cu castings

246–426 HB

Al-Si-Ni castings

336–426 HB

Al-Si castings

381–538 HB

Phosphor bronze castings

336–470 HB

Brass castings 470–672 HB

(a) Tensile strength (in psi) = multiplying factor × hardness.

Source: Ref 11, 12

More information on hardness tests and the estimation of mechanical properties is in the article “Selection and

Industrial Application of Hardness Tests” in this Volume. References 12 and 14 also contain information on the

application of hardness testing.

References cited in this section

11. W.J. Taylor, The Hardness Test as a Means of Estimating the Tensile Strength of Metals, J.R. Aeronaut.

Soc., Vol 46 (No. 380), 1942, p 198–202

12. George Vander Voort, Metallography: Principles and Practices, ASM International, 1999, p 383–385

and 391–393

13. R.T. Shield, On the Plastic Flow of Metals under Conditions of Axial Symmetry, Proc. R. Soc., Vol

A233, 1955, p 267

14. H. Chandler, Ed., Hardness Testing, 2nd ed., ASM International, 1999

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Torsion and Bending

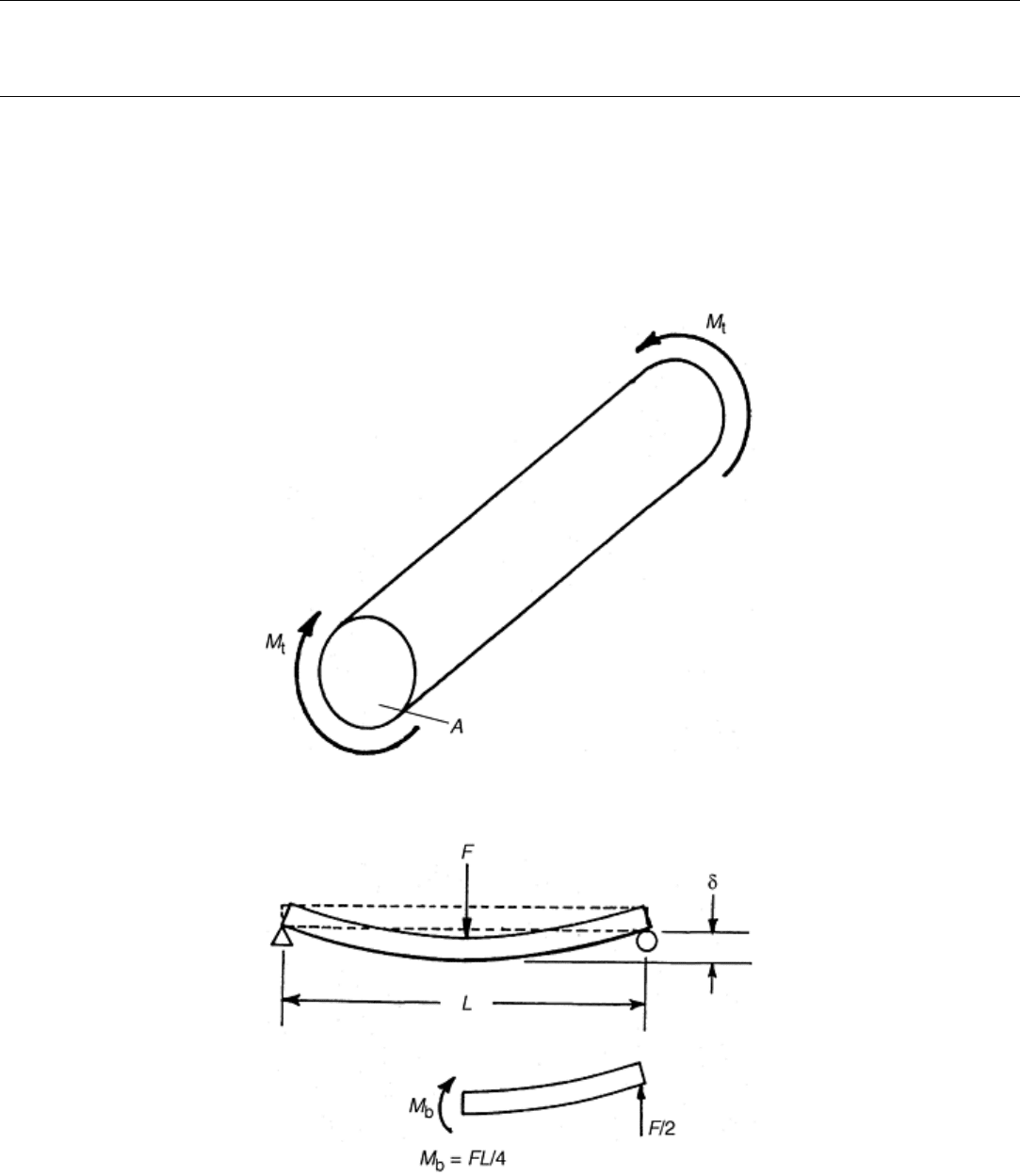
Instead of axial loads, the tie bar in Fig. 1 may be subjected to torsion moments about its axis on each end, as

shown in Fig. 6. This represents the loading in drive shafts or torsion bar suspensions, for example. In other

applications, the bar may be subjected to loads perpendicular to its axis resulting in a bending moment, as

shown in Fig. 7. Typical examples include leaf springs and structural beams.

Fig. 6 Bar under torsion. M

, applied torque. A, cross sectional area of the bar

Fig. 7 Bar under bending by a transverse load. F, applied force; L, length of the bar; M

, bending

moment

Shear Stress Distributions. In both torsion and bending, the shear strain (in torsion) and the longitudinal strain

(in bending) are zero at the centerline, or neutral axis, and increase linearly to maximum values at the outer

surfaces. As a result, the stress distributions are linear, as shown in Fig. 8 for torsion and Fig. 9 for bending.

Note that, in bending, the stress is tensile on the convex side of the bar and compressive on the concave side.

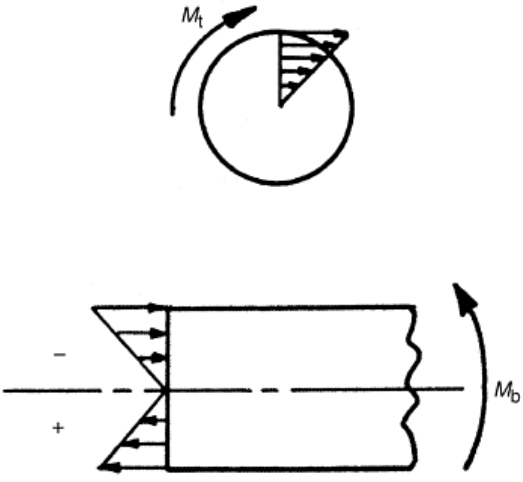
Fig. 8 Linear distribution of shear stress in torsion of a round bar. M

, applied torque

Fig. 9 Linear distribution of normal stress in bending. M

, bending moment

The shear stress distribution in torsion is given by (Ref 15):

τ = M

r/J

(Eq 10)

where τ is the shear stress, M

is the applied torque, r is measured from the axis, and J is the polar moment of

inertia (second moment about the axis of rotation) of the bar cross section. The influence of J in design is

discussed later in “Shape Design” in this article. More detailed descriptions of rotational shear (i.e., torsion) are

provided in the article “Fundamental Aspects of Torsional Loading” in this Volume.

The normal stress distribution in bending is given by (Ref 16):

σ = M

z/I

(Eq 11)

where σ is the longitudinal stress in the bar, M

is the bending moment, z is measured from the neutral axis, and

I is the moment of inertia (second moment about the bending axis) of the bar cross section. The role of I in

design is also discussed later in “Shape Design.” More detailed descriptions of bending stress and strain

behavior are provided in the article “Stress-Strain Behavior in Bending” in this Volume.

Design for Strength in Torsion or Bending. Design of bars under torsional or bending moments is based on

preventing the maximum surface stresses from exceeding the failure limit of the material. For example, in

torsion of a round bar, τ

max

occurs at r = D/2 (where D is the bar diameter) and must satisfy the design

condition:

max

= M

D/2J < τ

(Eq 12)

where τ

is the failure shear strength of the material at failure. This value may be the shear yield strength, τ

, or

the ultimate shear strength, τ

. Similarly, in bending, the maximum normal stress, σ

max

, occurs at z = H/2 (where

H is the thickness of a symmetrical beam) and must satisfy the design condition:

max

= M

H/2I < σ

(Eq 13)

where σ

may be the tensile yield strength, σ

, or the ultimate tensile strength, σ

, for failure on the convex side

of the bar. Compressive strengths apply to failure on the concave side of the bar.

In the same way that Eq 2 is used for design of bars under tensile loading, Eq 12 and 13 can be used to

determine the maximum torque, M

, or bending moment, M

, that can be transmitted by a specific bar geometry

(D and J, or H and I) and material (τ

or σ

). These equations can also be used to determine the geometric

parameters required to transmit a specified torque or bending moment with a given bar material. Alternatively,

Eq 12 and 13 can be used to select materials having the proper values of τ

or σ

to transmit a specified torque or

bending moment in a bar of given geometry.

As with the case of simple tension, the design equations for torsion and bending can be modified to include the

additional criteria of minimum weight or minimum cost. The material parameters for minimum weight or

minimum cost in this case depend on the geometric parameters that are fixed and those that are variable. For a

beam with the width undefined, the design parameters are (σ

/ρ) and (σ

/ρc), while for beams in which the

height is undefined, the design parameters are (σ

1/2

/ρ) and (σ

1/2

/cρ) (Ref 1, 7).

Design for Stiffness in Torsion or Bending. Elastic deflection of a bar under bending moments and elastic

twisting of the bar under torsion may lead to additional design limits. For example, in bending a simply

supported beam (Fig. 7), the deflection at the center point is (Ref 16):

δ = FL

/48EI

(Eq 14)

The beam stiffness is determined by the material parameter, E, and the geometry parameters, L and I. Beam

design to meet deflection limitations can be accomplished by proper material specification or by geometric

specifications.

Similarly, torsional rotation of a round bar is given by (Ref 15):

θ = M

L/GJ

(Eq 15)

where M

is the applied torque, L is the length of the bar, J is the polar moment of inertia, and G is the shear

modulus of elasticity. Design for torsional stiffness involves selection of the bar dimensions as well as the

material via its elastic property, G, which is related to other elastic properties by (Ref 15):

G = E/2(1 + ν)

(Eq 16)

Shape Design. Of particular interest in design of bars under torsion or beams under bending are the moments of

inertia, J and I. Since the stress distributions in each case are linear and reach a maximum at the surface, as

shown in Fig. 8 and 9, the best use of material is accomplished by distributing it near the surfaces rather than at

the center. For example, the value of J for a solid circular cross section is:

J = πD

/32

(Eq 17)

By removing material from the central region of the bar, which is under little stress, the torsional load carrying

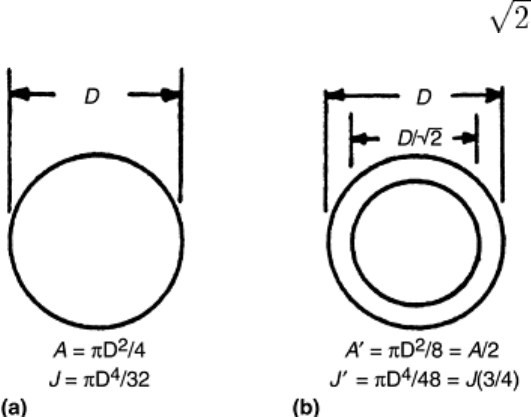
capacity is reduced slightly, but the area (and therefore weight) is reduced more significantly. Referring to Fig.

10, if one-half of the inner material is removed (i.e., inside diameter D

= D/ ), the weight is reduced by

50%, but the value of J is reduced by just 25%.

Fig. 10 Comparison of polar moment of inertia, J, for (a) solid and (b) hollow round bars. A, cross-

sectional area; D, diameter

Similarly, in bending, efficient material use is accomplished by placing material at the upper and lower

surfaces, as in the shape of an I-beam. To illustrate this, consider that the moment of inertia for a rectangle is

given by:

I = bH

/12

(Eq 18)

where b is the width and H is the height of the rectangle. Obviously, increasing H has a much larger effect on I

than increasing b. For example, as shown in Fig. 11, a rectangle that is 3 units thick and 9 units long has a value

of I that is 9 times larger in the vertical orientation compared to the horizontal orientation. However, if the same

amount of material is rearranged into an I-beam configuration, the value of I increases further by a factor of

nearly 3. Thus, weight savings in design for torsion and bending can be accomplished not only by selecting

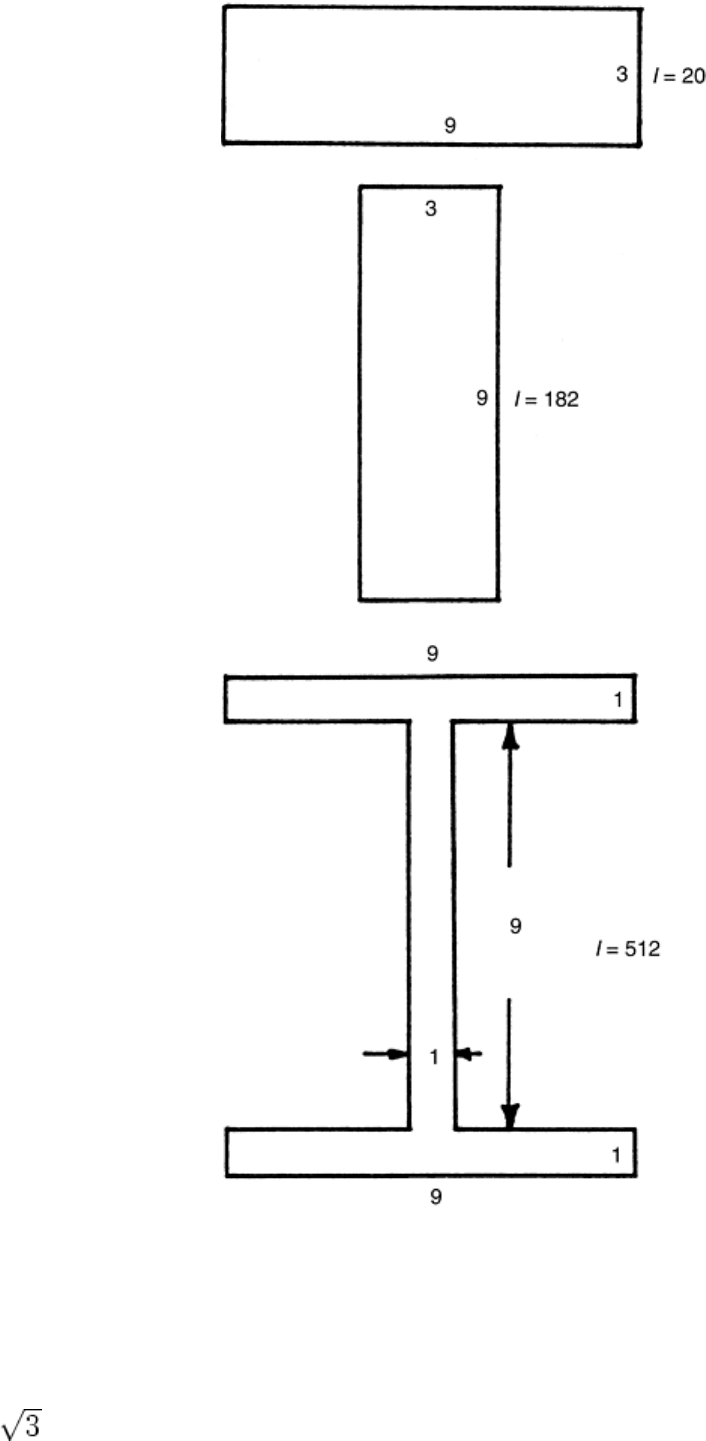
materials having high strength-to-weight ratios, but also by careful attention to the distribution of material in

the component.

Fig. 11 Comparison of moment of inertia, I, for three different arrangements of the same amount of

material

Mechanical Testing. Testing of materials for shear yield strength, τ

, to be used in Eq 12, or for tensile yield

strength, σ

, for use in Eq 13, can be accomplished through a tension test. If the material is isotropic and

homogeneous, the shear yield strength can also be calculated from the tensile yield strength (Ref 15):

= σ

(Eq 19)

Fracture strengths, however, must be measured in torsion and bend tests because the mechanisms or modes of

fracture may be different from those in tension testing.

Tensile yield strength, σ

, and shear yield strength, τ

, can also be derived directly from bending and torsion

tests using Eq 12 and 13. Accuracy will be limited, however, because in both cases yielding occurs initially at

the outside surfaces, so the effect on the measured loads is not as easily detectable as in the tension test, where

yielding occurs simultaneously across the entire section.

Torsion and bend tests are particularly useful in evaluating materials that have been given surface treatments

such as carburizing or shot peening to increase the strength of the surfaces and improve their resistance to the

high stresses at the surface generated by torsional or bending moments. Generally, the metallurgical structures

of such surfaces occur in a thin layer and cannot be produced easily in bulk form for measurement by tension

testing. Then, Eq 12 can be used to determine the strength, τ

, of the surface material in torsion, and Eq 13 can

be used to determine the strength, σ

, of surface material in bending. This approach is particularly useful for

determining fracture strengths of the surface materials.

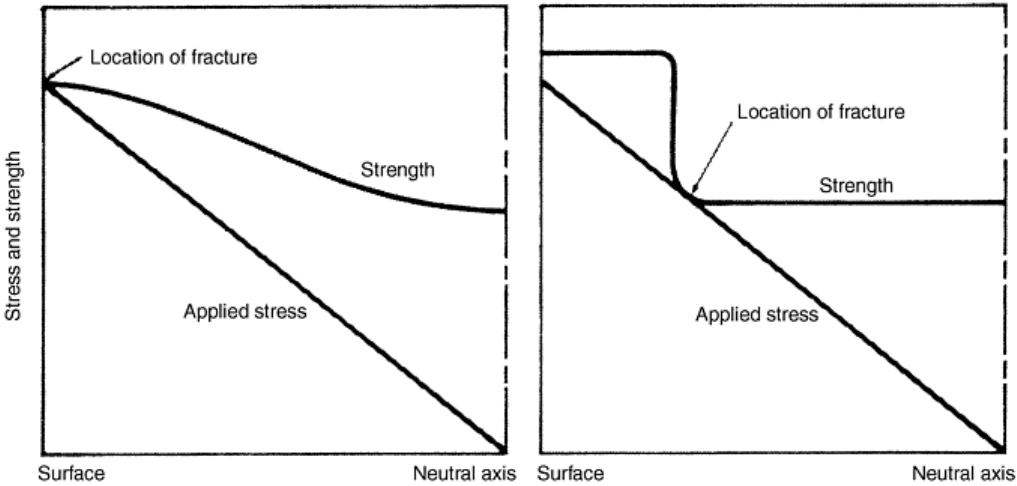
During bend or torsion testing of surface treated materials, however, certain precautions must be taken. First,

the orientation of the bending and shear stresses in the test specimens must be in the same orientation with

respect to the material microstructure as occurs in the actual components. Second, variations in material

strength beneath the surface must be considered in comparison with the linear distributions of stress in bending

and torsion shown in Fig. 8 and 9. Even though the surface material strength may be greater than the stress at

the surface (such as in a case hardened part), away from the surface at the neutral axis of the bar the strength

may decrease more rapidly than the applied stress, as illustrated in Fig. 12 (Ref 17). Then failure will occur

beneath the surface where the stress exceeds the local strength of the material. Clearly, it is important to

understand the strength distribution in a material in relation to the stress distribution acting on the material to

ensure that the product design prevents such insidious failures. Details on torsion and bend testing are covered

in separate articles in this Volume.

Fig. 12 Stress and strength distributions in a bar under torsion or bending. Failure occurs beneath the

surface if the material strength decreases more rapidly than the stress in the material. Source: Ref 17

Equation 14 for deflection of a beam also suggests an alternative method for measuring the elastic modulus, E,

of a material. For given geometry parameters, measured data pairs for force, F, and deflection, δ, lead to a

calculation of E. Alternatively, resonant frequency methods can be used to measure E in the beam geometry

shown in Fig. 7. The natural frequency of vibration of a beam is related to its geometry, density, and elastic

modulus. To carry out the measurement, the beam is vibrated by a transducer connected to a frequency

generator producing sinusoidal waves. By varying the frequency of the generator, the natural frequency is

determined when resonance occurs. Then the elastic modulus can be calculated from (Ref 18):

E = Cf

ρL

(Eq 20)