ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

where f is the resonant frequency, ρ is the material density, L is the beam length, H is the beam thickness, and C

is a constant. The shear modulus, G, can also be measured by sonic and resonant frequency methods in torsion.

Generally, resonant and sonic methods of measuring elastic properties are more accurate and easier to perform

than direct measurement of stress and strain in a tension or torsion test.

References cited in this section

1. Cambridge Engineering Selector, Granta Design Ltd., Cambridge, UK, 1998

7. M.F. Ashby, Materials Selection for Mechanical Design, 2nd ed., Butterworth-Heinemann, 1999

15. G.E. Dieter, Mechanical Metallurgy, 2nd ed., McGraw Hill, 1976, p 49–50, 79–80, 379, 381, 385

16. J.H. Faupel and F.E. Fisher, Engineering Design, John Wiley & Sons, 1981, p 102, 113, 230–235, 802

17. D.J. Wulpi, Understanding How Components Fail, ASM International, 1966, p 27

18. T. Baumeistes, Ed., Marks' Mechanical Engineers' Handbook, 6th ed., McGraw-Hill, 1958, p 5–106

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Shear Loading

The torsion test described above subjects material to shear stress in a rotational mode, but shear stresses also

occur in a translational mode. Such modes can be found, for example, in the end connectors of tie bars.

Design Examples. In an actual tie bar, the loads at each end of the bar in Fig. 1 would be applied through a pin

connector or a threaded coupling, for example, as shown in Fig. 13(a). If the tie bar were a composite material

(which cannot be threaded or drilled), the loads would most likely be applied through an adhesive lap joint, as

shown in Fig. 13(b).

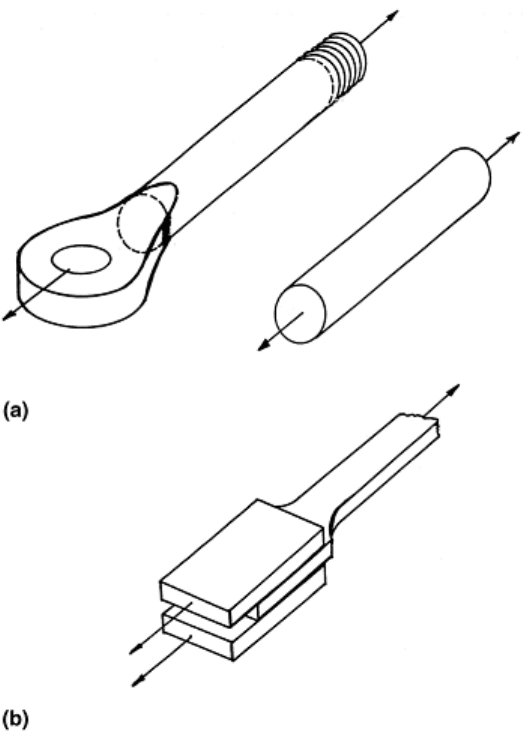
Fig. 13 Methods of connecting loads. (a) A load is applied to the tie bar in Fig. 1 by a pin/eye connector

and a threaded connector. (b) End loads are applied to a composite bar by adhesives.

In these and all other types of connectors, shear stresses occur in the transition from the connection to the

straight section of the bar. For example, Fig. 14(a) shows a pin through the eye of the tie bar and the forces

applied to the tie bar through a clevis. The pin, Fig. 14(b), is subjected to shear stresses along the dotted planes

between the eye of the tie bar and the clevis. Shear failure may occur along these planes. On the face view of

the eye on the tie bar, Fig. 14(c), shear also acts along the dotted planes from the hole to the end of the bar,

potentially leading to tear out of the end of the conductor. On the threaded end of Fig. 13(a), transmission of

load from a threaded connector to the tie bar also is carried by shear stresses at the root of the threads, shown by

the dotted lines in Fig. 15. In the lap joint shown in Fig. 13(b), shear would occur along the adhesive interfaces.

Concentrated shear stresses, similar to those shown in Fig. 14(b) and 14(c), also occur in many machine

elements, such as keys and keyways in drive shafts, shear pins, and splined couplings. These applications are

critical to the safe operation of machinery and require robust design methods using accurate material properties.

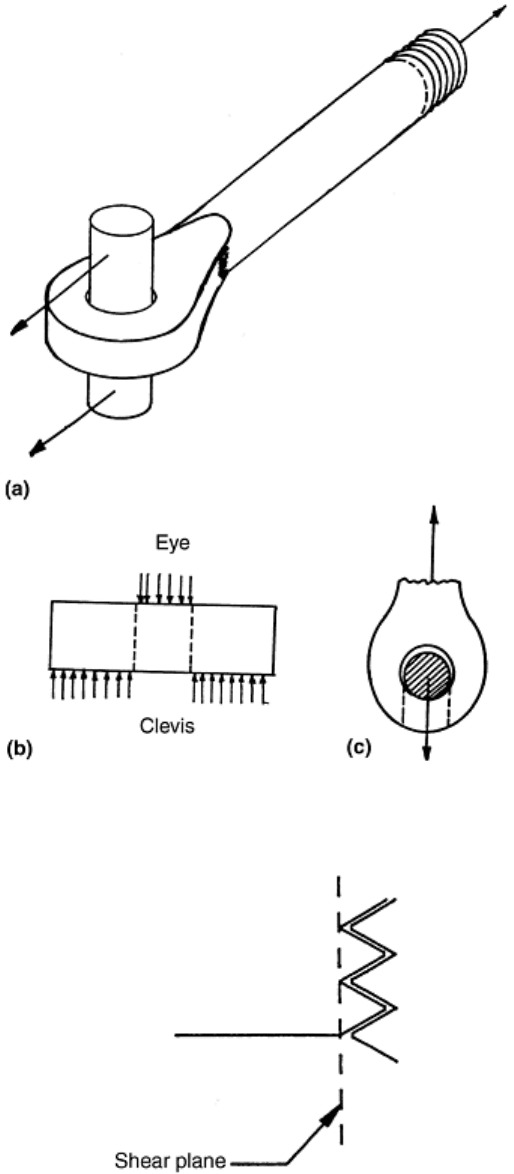
Fig. 14 Shear stresses in load end connectors. (a) A clevis and pin connected to the eye in Fig. 13(a). (b)

Shear planes in the pin. (c) Shear planes in the eye

Fig. 15 Shear planes in a threaded end connector

In all of these examples, the average shear stress acting on the shear planes is:

τ = F/A

(Eq 21)

where F is the load transmitted and A

is the total area of the shear planes. For design against failure, this shear

stress must be less than the shear strength of the material.

Mechanical Testing. Measurement of the shear yield strength of the material can be extracted from a tension

test by using Eq 19 if the material has an isotropic and homogeneous microstructure. The torsion test described

previously also can be used to determine the shear strength of the material. However, the torsion test measures

the shear strength of the material in rotational shear, but the applications shown in Fig. 13, 14, and 15 involve

linear shear along a plane through the material or along an interface. Linear shear behavior is affected

significantly by anisotropy of the microstructure of the material, and specialized tests have been developed to

determine the linear shear yield and fracture strength of materials. More details on torsion loading are in the

article “Shear, Torsion, and Multiaxial Testing” in this Volume.

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Complex Stresses

The previous sections describe the relatively simple uniform and linear stress distributions occurring during

tension, compression, torsion, bending, and shear. In all of these cases, one primary stress occurred.

Nonelementary shapes, however, lead to nonuniform, nonlinear, and multiaxial stresses, and these complex

stress states must be considered in a complete analysis for product design.

Constitutive Relations. To consider the effects of combined stresses in design, constitutive equations are

required that give the relationships between multiple stresses and strains. A one-dimensional example of a

constitutive relation is the combination of Eq 5 and 7, describing the elastic connection between uniaxial stress

and strain. Extending this behavior to three dimensions, if σ

is applied in the x-direction, the strain ε

= σ

occurs, and that same stress will generate transverse strains:

= ε

= -νε

= -νσ

/ E

(Eq 22)

This leads to the complete three-dimensional expressions relating elastic stresses and strains (Ref 15):

= (σ

- νσ

)/E

(Eq 23a)

= (σ

- νσ

)/E

(Eq 23b)

= (σ

- νσ

)/E

(Eq 23c)

A complete description of material behavior requires a description of yielding under multiaxial stresses.

Equations 2, 12, 13, and 21 express the conditions for yielding under the action of a single tensile or shear

stress. For three-dimensional stresses, a commonly used criterion that includes the effect of all stresses acting at

a point in a material is:

[(σ

- σ

)

+ (σ

- σ

)

+ (σ

- σ

)

+ 6τ

]

1/2

/ = σ

(Eq 24)

where σ

is the yield strength of the material in simple tension. Equation 24, known as the von Mises yield

criterion (Ref 19), relates all of the stresses acting in a material to its yield strength. Note that, in a torsion test

where normal stresses are zero and only one shear stress is applied, Eq 24 reduces to Eq 19, which enables

shear yield strength values for design to be determined from a simple tension test.

Equations 23a, 23b, 23c, and 24 are the constitutive relations for elastic deformation and yielding of an

isotropic material. More complex constitutive relations have been developed for anisotropic materials,

composites, and rate dependent materials. For failure by fracture, no simple criterion, such as Eq 24, exists to

express the effects of multiaxial stresses on failure.

Qualitative results from Eq 23a, 23b, 23c, and 24 lead to insights on the relationships between combined

stresses and strains. For example, in a plane-strain tension test (Fig. 16), a groove across the face of the

specimen will lead to stress σ

= F/tW where F is the applied load, t is the groove thickness, and W is the

specimen width. Under the action of this stress, the material in the groove will tend to contract in the thickness

direction, z, and in the width direction, y. There is no constraint preventing the material from contracting in the

thickness, so σ

= 0. In the width direction, however, the bulk material (thickness, T, much greater than t) on

each side of the reduced section prevents material from contracting. That is, ε

= 0. Then, from Eq 23a, 23b, and

23c:

= 0 = (σ

- νσ

)/E

(Eq 25a)

= νσ

(Eq 25b)

That is, a stress is generated in the y-direction because the natural tendency for the material to contract is

constrained. The strain in the thickness direction will be:

= -ν(σ

+ σ

)/E = -ν(1 + ν)σ

(Eq 26)

which is slightly larger than the strain that would have occurred with no constraint in the y-direction. More

complex interactions occur between three-dimensional stresses and strains in more complex geometries, and

these interactions are influenced strongly by the Poisson ratio, ν.

Fig. 16 Plane strain tension test specimen, showing the strains and stresses in the gage section

The multiaxial stresses in this example have an effect on yielding. The applied stress, σ

, combined with the

constraint of transverse strain in the y-direction, generates a stress in the y-direction given by Eq 25a and 25b.

The applied stress σ

required to cause failure by yielding can be found by substituting the stresses σ

= νσ

and

= 0 into Eq 24, giving:

(σ

- νσ

)

+ (νσ

)

+ (-σ

)

= 2σ

(Eq 27a)

= σ

/(1 - ν + ν

)

1/2

(Eq 27b)

Substituting the value of ν = 0.5 for material undergoing plastic deformation, σ

= 1.15 σ

; that is, because of

the constraint to contraction in the y-direction of the geometry shown in Fig. 16, the stress required to yield the

material is 15% higher than the axial stress required to yield the material if it were in simple tension.

Following are further examples of basic design stress conditions that involve nonlinear stress distributions and

multiaxial stresses.

Stress Concentrations. In the transition from the pin connector to the uniform cylindrical part of the tie bar (Fig.

13a), the irregular geometry leads to concentrations of stress around the hole in the tie bar. The load applied by

the pin is distributed as a nonuniform stress across the eye cross section, as shown in Fig. 17. Although the

average stress on the cross section equals the load divided by the area, peak values of the stress occur at the

inside of the eye.

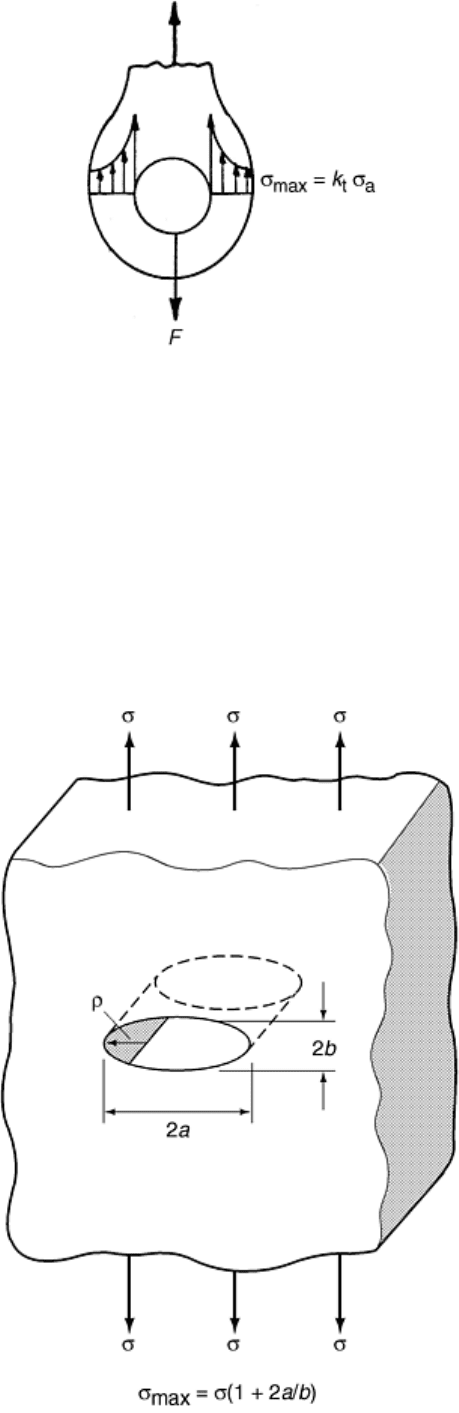
Fig. 17 Stress distribution on a cross section through the eye shown in Fig. 13(a)

Such concentrations of stress occur in all geometric irregularities such as fillet radii, notches, and holes. A

simplistic but useful expression for the stress concentration is given by (Ref 19):

max

= k

≈ (1 + 2a/b) σ

(Eq 28)

where k

is the stress concentration factor, σ

is the average stress, a is the dimension of the geometric

irregularity perpendicular to the applied load, and b is the dimension parallel to the load (Fig. 18). In Fig. 17,

for example, a = b, so the stress concentration factor is 3. For very small cracks perpendicular to the load, a is

much greater than b so the stress concentration becomes 2 a/b. Stress concentration factors for a wide range of

practical geometries have been developed through extensive experimentation and analysis (Ref 16, 20). Failures

usually initiate at these points of stress concentration and must be considered in all product designs.

Fig. 18 Stress concentration around a flaw. Source: Ref 19

Pressure Vessels. Multiaxial stresses occur in shells subjected to internal or external pressure. Examples include

tanks containing fluids, vessels containing a high-pressure and high-temperature chemical reaction (such as in

petroleum refining), dirigibles, and submarine pressure hulls. Proper design of such pressure vessels must

account for the multiaxial stresses.

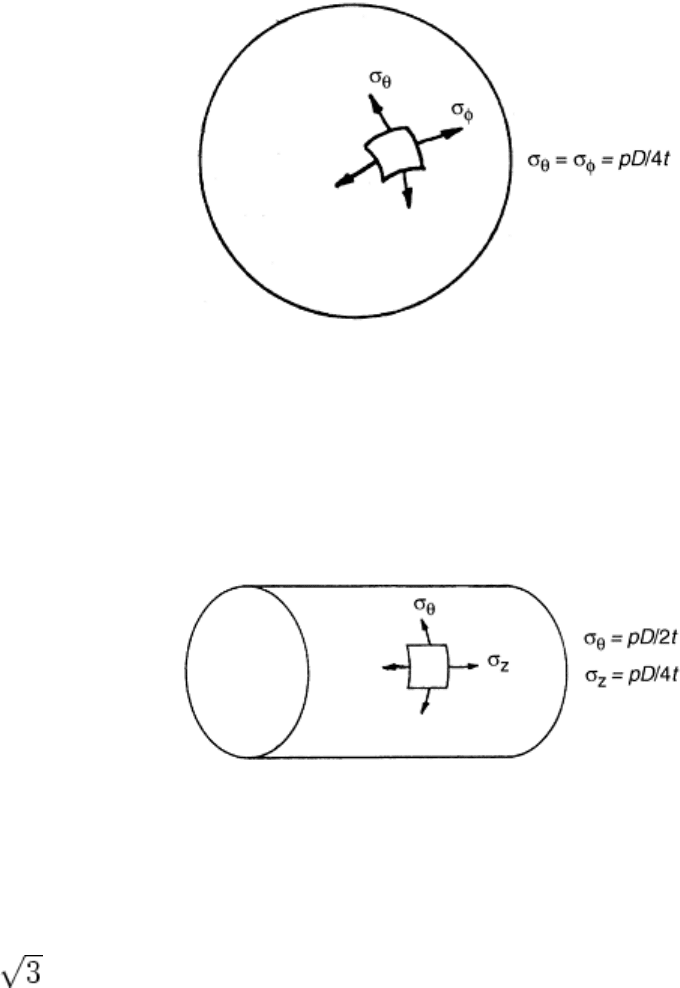
A spherical shell containing pressure, for example, has equal stresses in any two perpendicular directions

tangent to the sphere (Fig. 19), given by (Ref 22):

= σ

= pD/4t

(Eq 29)

where p is the internal pressure, D is the spherical diameter, and t is the wall thickness. Note that for D much

greater than t, these stresses are much larger than the pressure, and stress through the thickness σ

≈ 0.

Fig. 19 Stresses in the wall of a spherical pressure vessel

A cylindrical pressure vessel wall will have a stress in the circumferential, or hoop, direction (Fig. 20), given by

(Ref 16):

= pD/2t

(Eq 30a)

and a stress in the axial direction given by:

= pD/4t

(Eq 30b)

Fig. 20 Stresses in the wall of a cylindrical pressure vessel

Failure by yielding of a spherical pressure vessel can be found by substituting Eq 29 into Eq 24, giving:

max

= 4σ

t/D

(Eq 31)

For the cylindrical pressure vessel, substituting Eq 30a and 30b into Eq 24 gives:

max

= (4 / )σ

t/D

(Eq 32)

In all pressure vessel applications, the stresses in the wall, given by Eq 29, 30a, and 30b, may be further

complicated by stress concentrations due to holes for inlet and outlet piping.

In cases where the wall thickness is much less than the diameter, the stresses given by Eq 29, 30a, and 30b are

nearly uniform through the thickness. For pressure containment where the wall thickness is a significant

fraction of the diameter, such as in metalworking dies, the stress distribution is nonuniform with peak values at

the inner surface (Ref 16). In these cases as well, Eq 24 is used to evaluate the initiation of failure by yielding.

Bearing Loads. Close examination of the pin end connector in Fig. 13(a) shows that the pin rests in a circular

hole at the end of the tie bar. For ease of attachment to the connector, the pin diameter is smaller than the hole

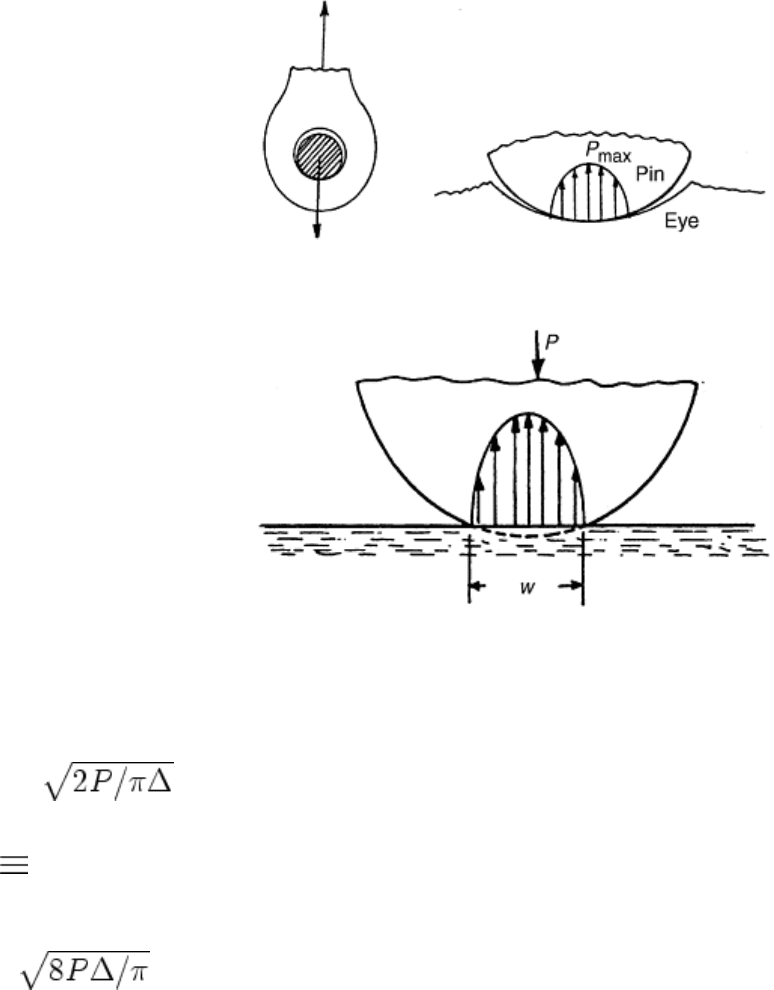
diameter. As a result, the load transmitted from the pin to the inside surface of the hole occurs over a small area

of contact, leading to high local pressures, as shown in Fig. 21. The pressure distribution in bearing contacts of

this type is generally elliptical because the greatest elastic deformation occurs at the center of the contact zone.

Figure 22 shows this more clearly in the contact pressure between a flat plate and a cylinder. Similar types of

bearing loads and the accompanying elliptical pressure distributions occur in journal bearings, ball and roller

bearings, gear tooth contacts, and railroad wheel/rail contacts. The nature of the contact pressure distributions

and the internal distribution of stresses resulting from these loads have special implications regarding material

testing and selection.

Fig. 21 Contact stresses between a pin and eye

Fig. 22 Flattening and contact pressure distribution between a roller and flat plate

In roller-on-roller contacts, the elliptical pressure distributions in Fig. 21 and 22 have peak pressures given by

(Ref 21):

max

(Eq 33a)

where P is the load per unit length of contact and

Δ [1/(1/D

+ 1/D

)] [(1 - ν1

)/E

+ (1 - ν2

)/E

]

(Eq 33b)

where D

and D

are the diameters of the rollers, and ν and E are the elastic properties of the materials in

contact. The width, w, of the contact zone between the rollers is given by:

w =

(Eq 34)

In addition to the normal contact pressure shown as σ

in Fig. 22, elastic deformation in the contact zone also

generates σ

parallel to the surface and σ

parallel to the axes of the rollers (perpendicular to the view in Fig.

21). In this case, σ

has the same magnitude and elliptical distribution as σ

. Beneath the surface in Fig. 22, all

of the stresses decrease because the contact load is spread over a larger area. Stress analysis leads to the stress

distributions (Ref 21):

= - w/2Δζ

(Eq 35a)

= - (ζ - z′)

w/2Δζ

(Eq 35b)

= - ν(ζ - z′) w/Δζ

(Eq 35c)

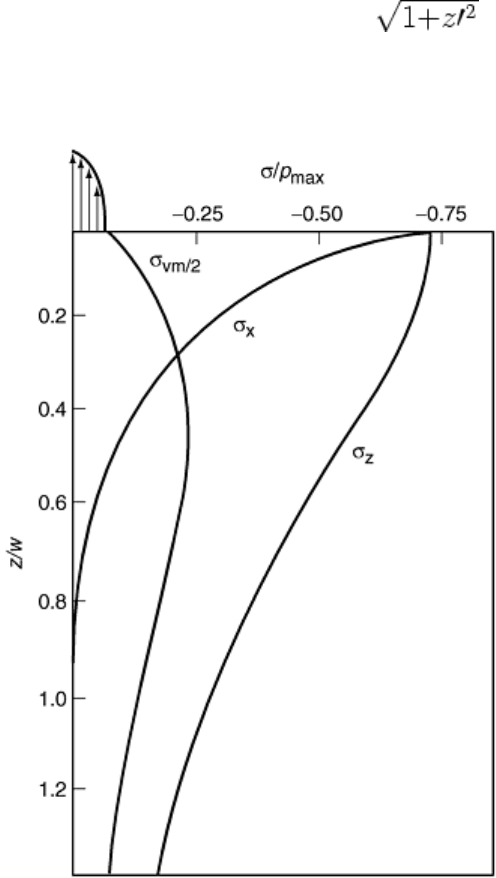
where z is the distance beneath the contact surface, z′ = 2z/w, and ζ = .

These stresses are plotted in Fig. 23, which shows that σ

decreases more rapidly than σ

. The von Mises stress

is also plotted, which shows a maximum at a distance 0.4w beneath the surface (where w is the contact

width calculated from Eq 34). Subsurface failure as a result of these stresses is common in rolling contact

configurations such as Fig. 22.

Fig. 23 Stresses beneath the contact zone in Fig. 22

Finite Element Analysis. For complex stress problems that are not easily solved using the basic loading

situations (or their combinations) described previously, finite element analysis is commonly used. Over the past

four decades, the finite element method has evolved from a structural analysis tool to a set of refined

commercial programs that are invaluable aids in modern design. Much of this utility is a result of the

availability of more rapid and powerful computers, improved numerical methods for solving the equations, and

enhanced computer graphics for display of the results.

Finite element analysis reduces the infinite number of points in a prescribed product geometry to a finite

number of elements bound by a finite number of points. The behavior of each element in a finite-element grid is

governed by the same principles of equilibrium as in the tensile, compressive, torsional, and bend loadings

described previously in this article, and by the material behavior described through constitutive equations (Eq

23a, 23b, 23c, and 24).

The beauty of finite element analysis for design is that it allows consideration of complicated geometries and

any type of material for which the properties are known. Finite element analysis methods thus assist in the

specification of geometry and material, which are the two primary objectives of design for mechanical

applications. Evaluating small changes in geometry or variations in material properties via finite element

modeling permits design optimization.

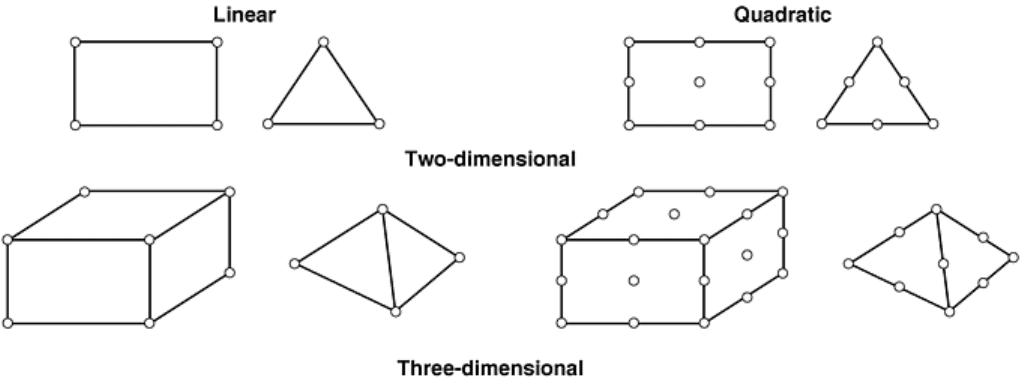
In the application of finite element analysis (Ref 22, 23), first the product geometry is described by a collection

of two-dimensional or three-dimensional elements, such as those shown in Fig. 24. The choice of element type

depends on the problem geometry and loading. From displacements of the nodal points in each element, the

deformations and strains in the element are defined. Then the material constitutive equations (e.g., Eq 23a, 23b,

and 23c) relate these strains to the stresses in each element. Each node is connected to two or more elements, so

there is interdependence between neighboring elements.

Fig. 24 Examples of element geometries used for finite element models

The next step is to define the boundary conditions (externally applied loads at the appropriate nodes) and

constraints (identification of the nodes that are constrained from moving in at least one direction). This is a very

important key to development of an accurate model and is based on mechanical insight of the person doing the

modeling.

Energy methods are used to determine the interdependent nodal displacements (and stresses and strains) that

minimize the total energy of the system. The resulting myriad of linear algebraic equations are then solved for

all of the nodal displacements such that the stresses and deformations are compatible from element to element

and are consistent with the externally applied loads and nodal constraints.

As an example, Fig. 25 shows a strip under tension and containing a hole, which was shown previously to cause

a concentration of stress. The elements used for the analysis are quadrilateral to conform to the overall

geometry of the part (Ref 24). In the vicinity of the hole, the elements are distorted to conform to the shape of

the hole. In addition, the number of elements per unit area is increased in the vicinity of the hole because the

stresses change rapidly. Taking advantage of symmetry, one-quarter of the geometry is considered to reduce the

number of elements, nodes, and equations to be solved.