ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

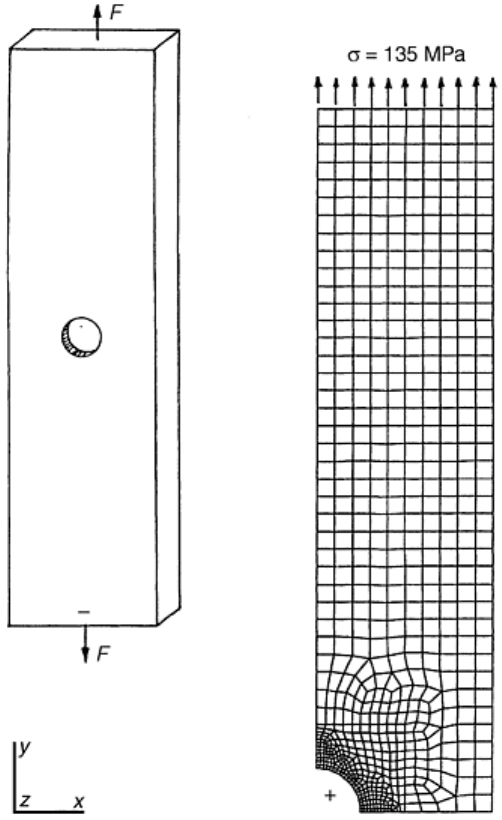
Fig. 25 Finite element model of a strip under tension and containing a hole. Source: Ref 24

Along the vertical line of symmetry, each nodal point is permitted to move vertically but not laterally. Along

the horizontal line of symmetry, each node is permitted to move laterally but not vertically. These constitute the

constraints on the problem.

At each of the nodal points along the upper surface, equal loads are applied that add up to the total applied load.

Alternatively, uniform small displacements in the vertical direction can be applied to each node along the upper

surface. This constitutes the loading for the problem. The material behavior is represented by elastic modulus,

E, and Poisson ratio, ν, in the constitutive equations, Eq 23a, 23b, and 23c.

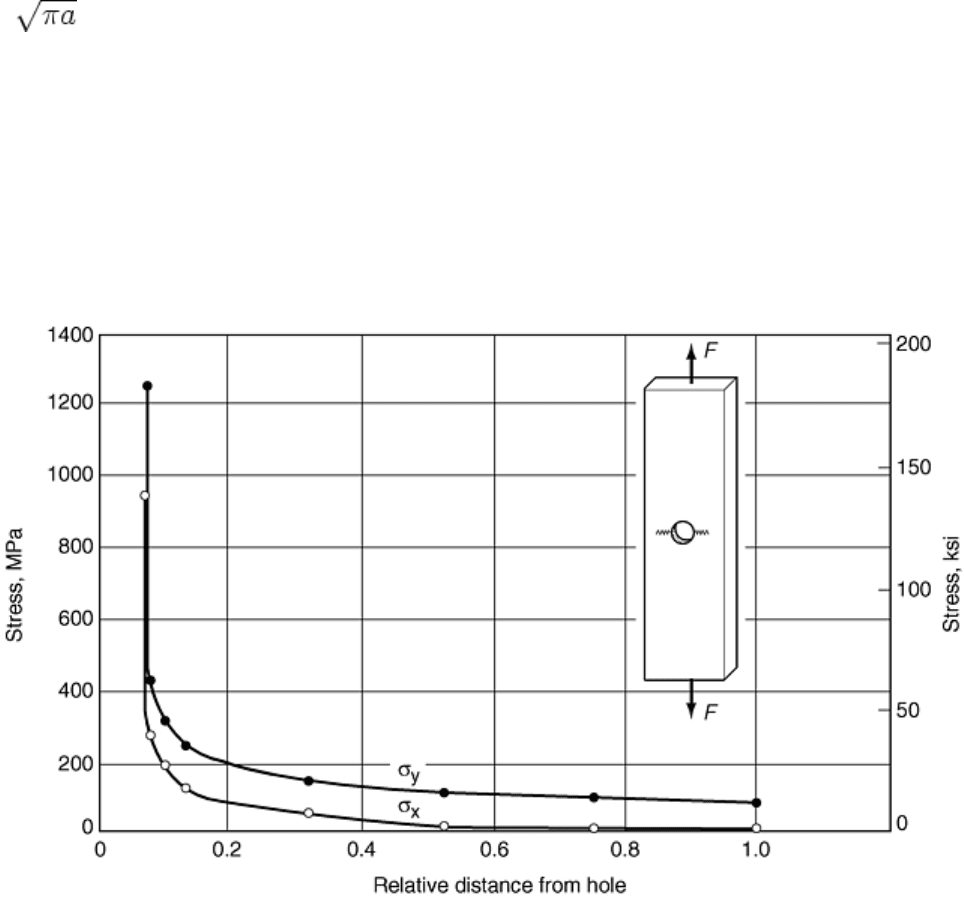
Results of solution of the simultaneous equations for all elements are shown in Fig. 26. Note that the axial

stress, σ

, along the horizontal plane through the hole has a peak value at the edge of the hole. Also, a small

lateral stress distribution, σ

, occurs along the horizontal plane of symmetry. Note that, along the vertical

centerline, the axial stress is zero at the hole and then increases to the applied stress, while the lateral stress is

compressive.

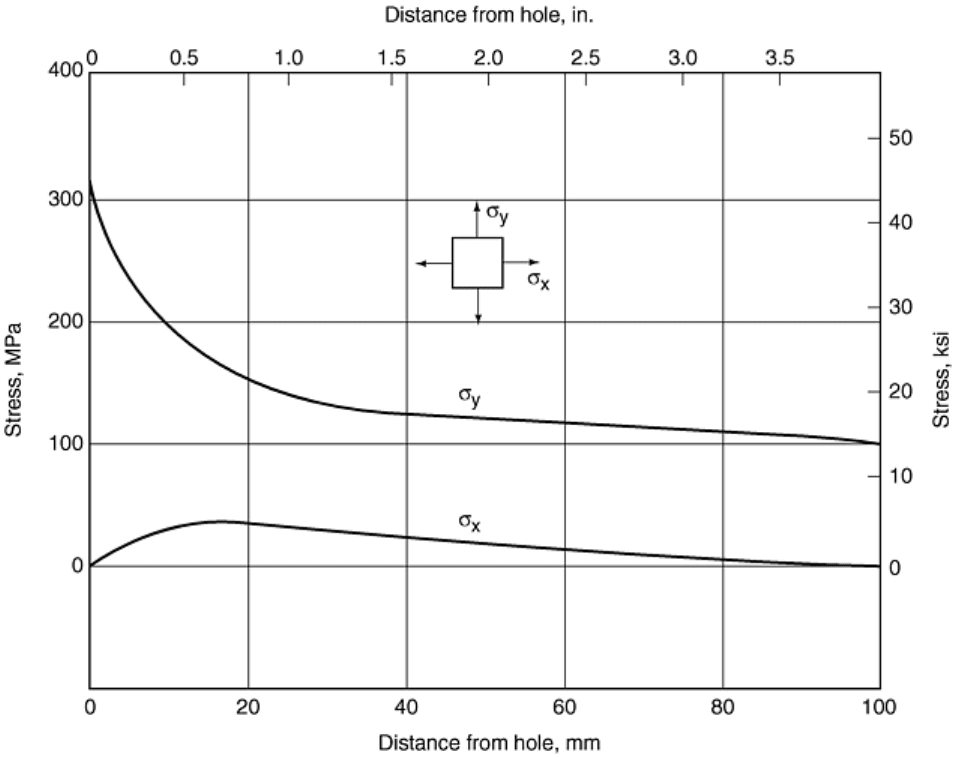
Fig. 26 Stress distributions calculated for the model shown in Fig. 25. Source: Ref 24

To evaluate failure by yielding, the stresses in each element of the model can be substituted into Eq 24. The

resulting stress magnitude is called the von Mises stress and can be compared to the material yield strength, σ

to determine if yielding will occur. For example, Fig. 27 shows a contour plot of the von Mises stress for the

problem shown in Fig. 25. Note that yielding would occur first at the inside of the hole and propagate along a

45° plane, illustrated by the band of high von Mises stress.

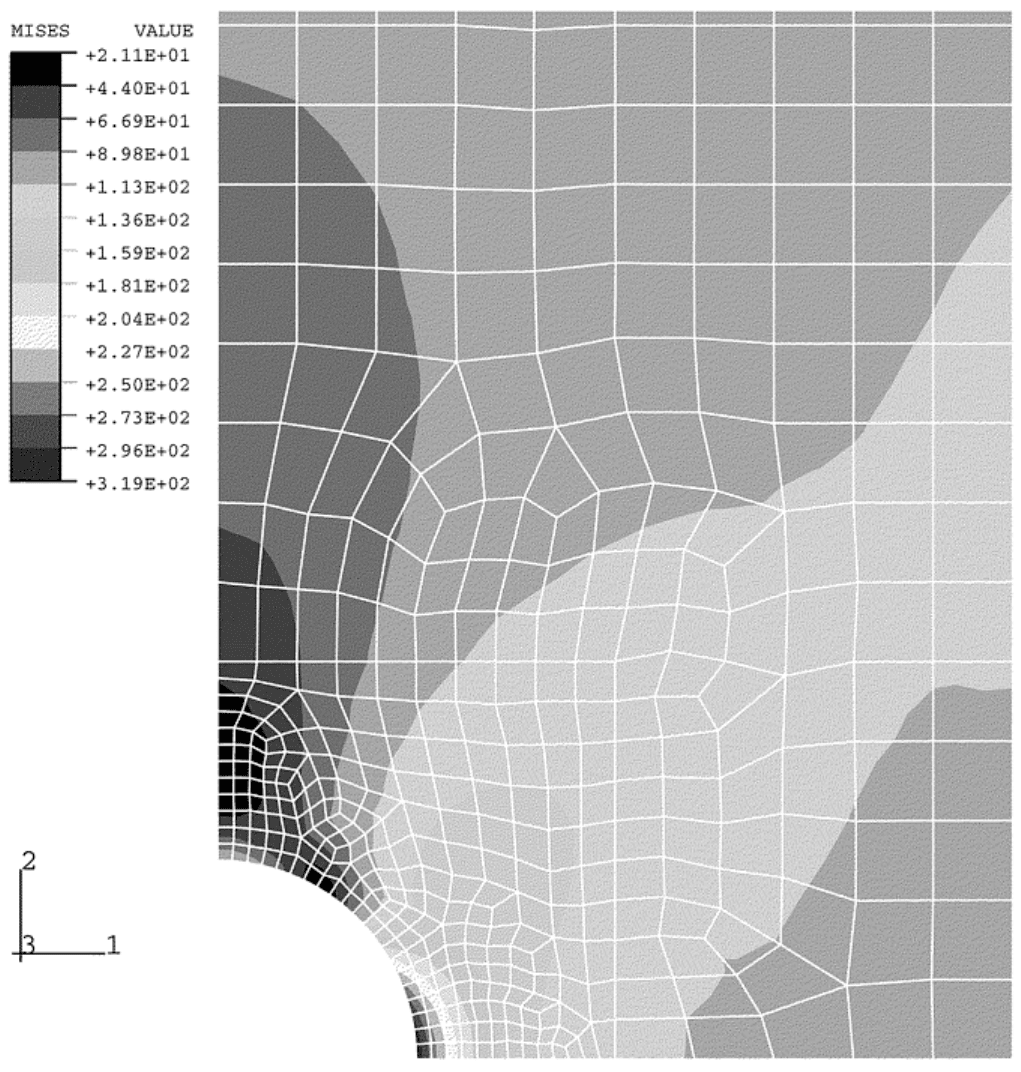
Fig. 27 Contour plot of von Mises stress for the model in Fig. 25. Source: Ref 24

As another example, a finite element analysis of the contact bearing load, described previously in Fig. 22, is

shown in Fig. 28 (Ref 24). A contour plot of the calculated von Mises stress (Fig. 29) shows a potential

subsurface failure point, as described previously by classical stress analysis (Fig. 22).

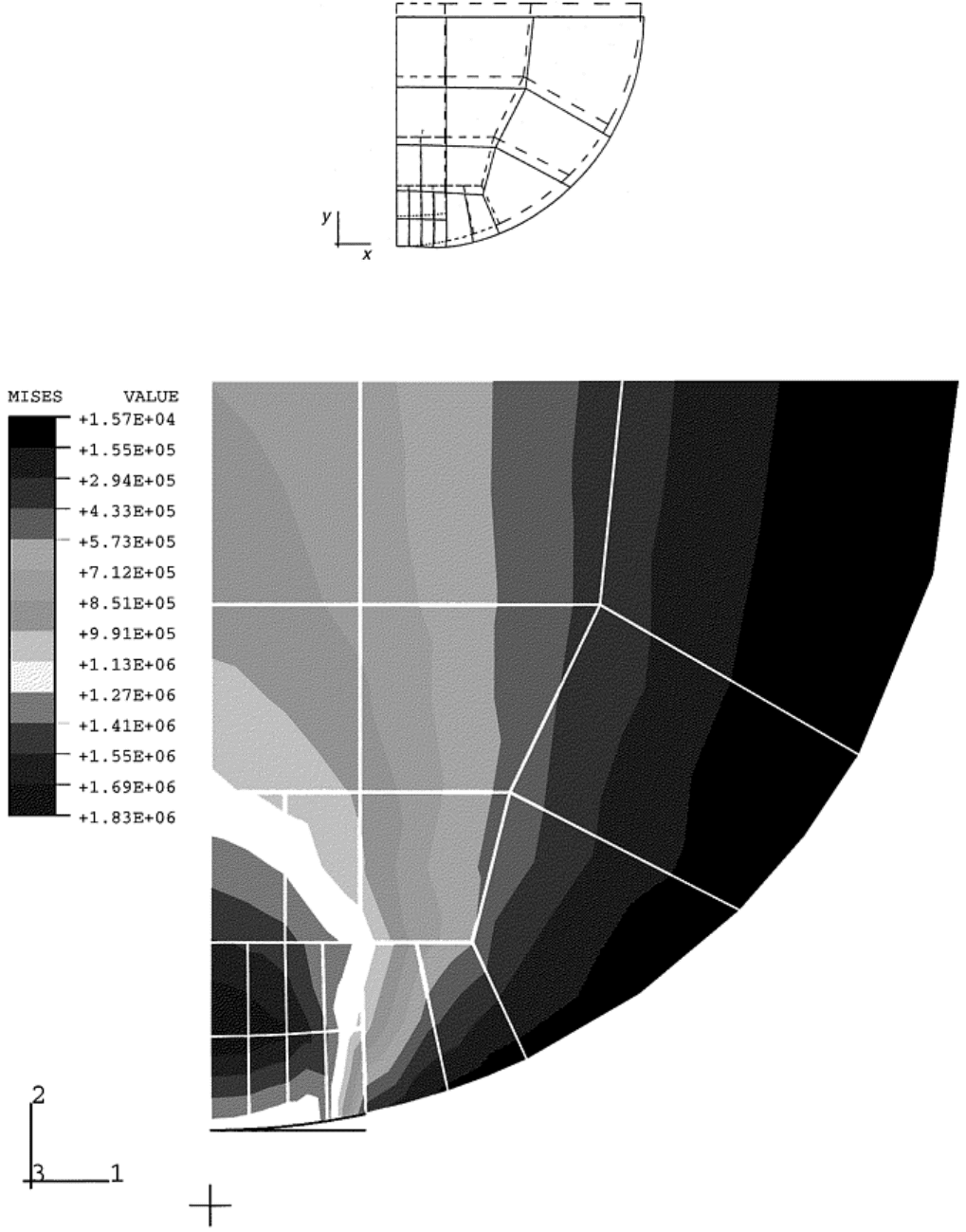
Fig. 28 Finite element model for contact stresses between a roller and flat plate, as in Fig. 22. Source: Ref

Fig. 29 Contour plot of von Mises stress beneath the zone of contact

These examples illustrate that finite element analysis tools provide deep insight into the mechanical behavior of

materials for product design, but physical validity of the analytical results is a prime concern for designers who

make decisions based on these results. Valid results depend on proper definition of the problem in terms of the

meshing (element shape and size), loading (boundary conditions and constraints), and material characteristics

(constitutive relations). Setting up a valid problem and evaluating the results are greatly enhanced by

knowledge of the stress, strain, and mechanical behavior of materials under the basic loading conditions

presented in the previous paragraphs. Often, the cost and time for finite element analysis can be precluded by

learned application of the knowledge of the basic modes of loading. This is the basis for the Cambridge

Engineering Selector (Ref 1). On the other hand, some problems are so complex that only finite element

analysis can provide the necessary information for design decisions. Analysts' and designers' skill and

experience are the bases for judgment on the level of sophistication required for a given design problem.

Additional information on finite element methods is provided in the article, “Finite Element Analysis” in

Materials Selection and Design Volume 20 of ASM Handbook.

Material Testing for Complex Stresses. In all of the cases given above for complex stresses, the tensile yield

strength and the elastic properties, E and ν, are the key material parameters required for accurate design

analyses. The yield criterion, using the tensile yield strength, σ

, is used to predict failure by yielding. All of

these material parameters can be determined by tension testing.

The prediction of failure by yielding is also useful for prediction of the sites for fracture since localized yielding

usually precedes fracture. Final failure by fracture, however, cannot be related to any single criterion or simple

test. The following paragraphs describe approaches to material evaluation for various forms of failure by

fracture.

References cited in this section

1. Cambridge Engineering Selector, Granta Design Ltd., Cambridge, UK, 1998

15. G.E. Dieter, Mechanical Metallurgy, 2nd ed., McGraw Hill, 1976, p 49–50, 79–80, 379, 381, 385

16. J.H. Faupel and F.E. Fisher, Engineering Design, John Wiley & Sons, 1981, p 102, 113, 230–235, 802

19. R.W. Hertzberg, Deformation and Fracture Mechanics of Engineering Materials, 2nd ed., John Wiley

& Sons, 1983, p 240, 287, 288, 436–477

20. W.C. Young, Formulas for Stress and Strain, 5th ed., McGraw-Hill, 1975

21. S.P. Timoshenko and J. Goodier, Theory of Elasticity, 3rd ed., McGraw Hill, 1970, p 418–419

22. O.C. Zienkiewicz, The Finite Element Method in Engineering Science, 4th ed., McGraw Hill, 1987

23. K.H. Heubner, et al., The Finite Element Method for Engineers, 3rd ed., John Wiley & Sons, 1995

24. ABAQUS/Standard, Example Problems Manual, Vol 1, Version 5.7, 1997

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Fracture

The design approaches given in preceding sections of this article were based on prevention of failure by

yielding or excessive elastic deflection. While the yield strength for ductile materials is below their tensile

strength, it is well known that failure by fracture can occur even when the applied global stresses are less than

the yield strength. Fractures initiate at localized inhomogenieties, or defects, in the material, such as inclusions,

microcracks, and voids. Previously it was shown that geometric inhomogenieties in a part lead to

concentrations of stress (Fig. 18 and Eq 28). Material defects, generally having a sharp geometry (a much

greater than b) lead to very high localized stresses.

Considering such defects in design against fracture requires looking beyond stress and elastic deformation to

the combination of stress and strain, or energy per unit volume. Defects are commonplace in the

microstructures of real materials and are generated both by materials processing and by service loads and

environments. Under certain conditions, these defects can grow, unsteadily, leading to rapid and catastrophic

fracture. This condition was first described by Griffith (Ref 25), who noted that a defect would grow when the

elastic energy released by the growth of the defect exceeded the energy required to form the crack surfaces. The

excess energy in the system, then, continuously feeds the fracture phenomenon, leading to unstable

propagation. The driving energy from defect growth is a function of the applied stresses (loading, part, and

defect size geometry), and the energy for crack surface formation is a function of the material microstructure.

Details of the development can be found in Ref 19 and 27 and the Section “Impact Toughness Testing and

Fracture Mechanics” in this Volume.

Design Approach. For design and materials selection to avoid fast fracture, the net result of these considerations

is the basic design equation for stable crack growth (Ref 19):

K = Yσ < K

(Eq 36)

where K is the stress intensity factor, Y is a factor depending on the geometry of the crack relative to the

geometry of the part, σ is the applied stress, a is the defect size or crack length, and K

is a critical value of

stress intensity. K must be less than K

for stable crack growth.

The stress intensity K represents the effect of the stress field ahead of the crack tip and is related to the energy

released as the crack grows. For example, Fig. 30 shows the results of finite element analysis of the stresses in

the vicinity of a crack growing from a hole. The high level and distribution of stresses ahead of the crack tip all

contribute to the stress intensity factor. When the stress intensity exceeds a critical value, K

, the energy

released exceeds the ability of the material to absorb that energy in forming new fracture surfaces, and crack

growth becomes unstable. This critical value of the stress intensity is known as the fracture toughness of the

material.

Fig. 30 Finite element calculation of stresses in the vicinity of a crack at the edge of a hole in a strip

under axial tension

Equation 36 can be viewed in the same way as Eq 2 for tensile loading and Eq 12 and 13 for bending and

torsion. The stress intensity factor, K, in Eq 36 is equivalent to stress, σ in Eq 2, 12, or 13. While the stress is

defined for each case by the applied load and geometry of the part, stress intensity is defined by the applied

stress (load and part geometry) and the geometry of the crack relative to the geometry of the part, which is

expressed by the factor Y. The important difference is that more information is given in the stress intensity

factor since it involves the defect or crack size, which becomes an additional design parameter. Values of Y can

be found in Ref 19 and 26, among others, for some common part geometries and crack configurations.

Alternatively, finite element analysis can be used to determine K. The fracture toughness of the material, K

, on

the right side of Eq 36 is equivalent from a design perspective to the material strength, σ

, in Eq 2, 12, and 13.

In applying Eq 36, if the material is specified and the stress is known from the loading requirements, then the

maximum flaw size that can be tolerated is a

max

= K

/σ

πf

(or a

max

= Y

/σ

π). This gives a clear objective

for nondestructive inspection of flaws in the product. Alternatively, if the material is specified and a maximum

flaw size is specified that can be easily seen by visual inspection, then the maximum stress that can be applied

is σ

max

= YK

/ . On the other hand, if the stress and maximum flaw size are known, Eq 36 defines the value

of K

required to prevent fracture and is used for material selection from tables of fracture toughness.

One application of the fracture criterion in Eq 36 is the design of pressure vessels, using a leak-before-break

philosophy. If the pressure vessel contains a flaw that grows to extend through the pressure vessel wall without

causing unstable fracture, then the internal pressurized fluid will leak out. On the other hand, if the flaw size in

the pressure vessel is above the critical flaw size yet less than the wall thickness of the vessel, fracture will

occur catastrophically. In Fig. 31, a flaw is shown having grown through the pressure vessel wall (Ref 19). If

the critical flaw size is taken as the thickness of the pressure vessel wall, then Eq 36 gives σ

max

= YK

/ ,

where t is the thickness of the wall. Equations 29, 30a, and 30b can be used to define the applied stress in the

pressure vessel wall and its relation to the internal pressure. Then, for a given material and its fracture

toughness, K

, the maximum stress and internal pressure is determined. Conversely, for a given pressure (and

stress in the wall), the required value of fracture toughness is given by K

= σ /Y.

Fig. 31 Flaw in a pressure vessel wall. Source: Ref 19

Mechanical Testing. The crack opening mode described in this example is known as mode I, or crack opening

perpendicular to a tensile stress (Fig. 32), which is the most common mode of fracture. Mode I cracking occurs,

for example, in the tensile loading of the tie bar shown in Fig. 1, in the stress concentration around the eye in

the end connector (Fig. 16) and in bending (Fig. 7 and 9). In this case, the critical stress intensity of the

material, or fracture toughness, is designated K

. However, two other crack opening modes are possible, as

shown in Fig. 32. Mode II occurs in linear shear, as depicted in Fig. 14 and 15, while mode III occurs in

torsional shear (Fig. 6 and 8). The critical stress intensity for these modes are denoted by K

IIc

and K

IIIc

. The

mode of potential fracture prescribes the test and approach used for measurement of the respective fracture

toughness values.

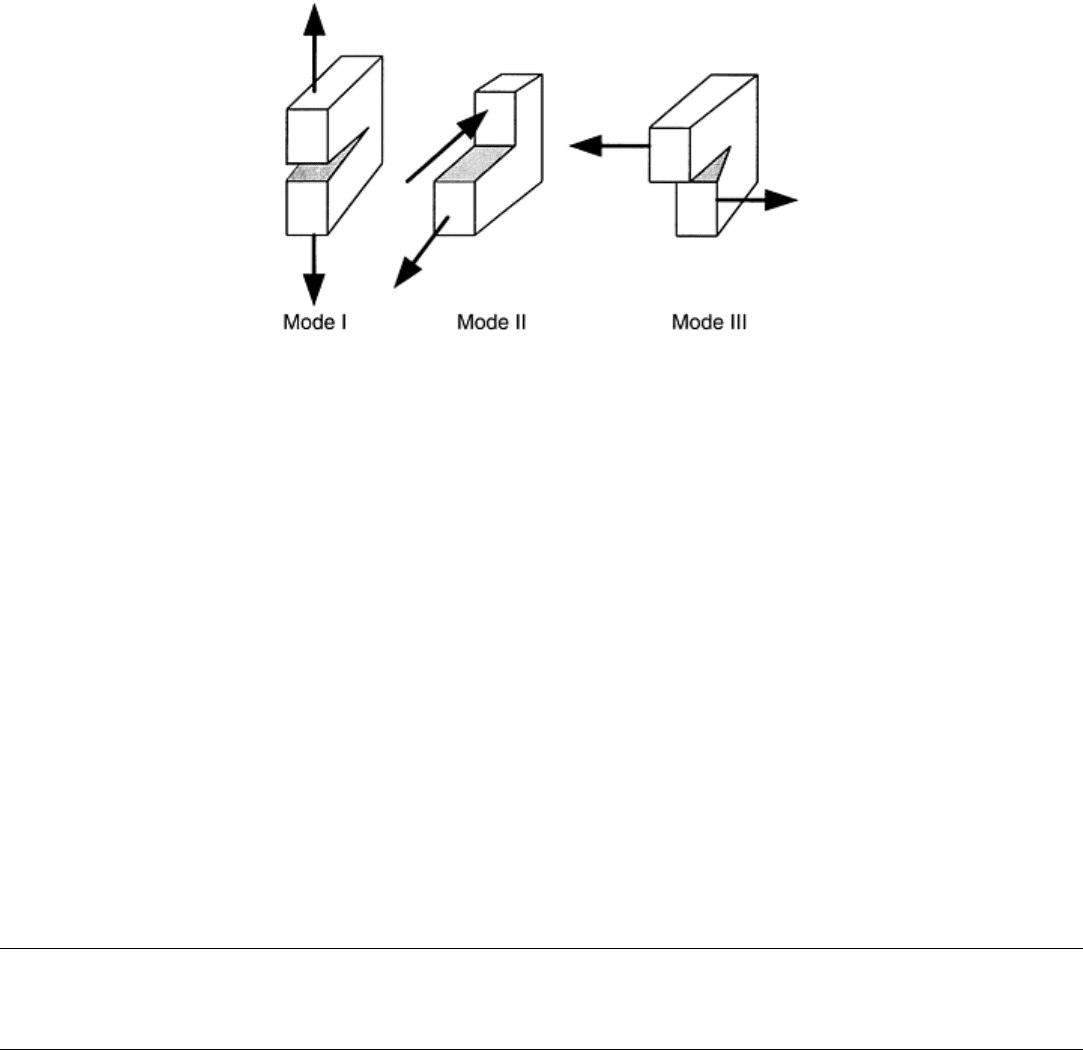
Fig. 32 Three crack opening modes

The material property to be determined for design against fracture is the fracture toughness, K

, to be used in Eq

36. The critical stress intensity, K

, or fracture toughness in mode I, for example, can be measured by a

compact tension test as well as other standardized test specimens and procedures, as described in the Section

“Impact Toughness Testing and Fracture Mechanics” in this Volume. In addition, fracture toughness values can

be correlated with Charpy test measurements of toughness for certain steel alloys (Ref 27).

References cited in this section

19. R.W. Hertzberg, Deformation and Fracture Mechanics of Engineering Materials, 2nd ed., John Wiley

& Sons, 1983, p 240, 287, 288, 436–477

25. A.A. Griffith, Trans. ASM, Vol 61, 1968, p 871

26. A.F. Liu, Structural Life Assessment Methods, ASM International, 1998

27. J.M. Barsom, Engineering Fracture Mechanics, Vol 7, 1975, p 605

Overview of Mechanical Properties and Testing for Design

Howard A. Kuhn, Concurrent Technologies Corporation

Fatigue

In the previous discussion, the various loads and the resulting stress distributions are defined for static

conditions. In most design applications, however, parts and components are subjected to cyclic loads. In this

case, the peak amplitude of a load cycle (σ

max

in Fig. 33) is the maximum value of applied stress, which can be

analyzed by the equations for static stress distributions (for example, from Eq 1, 12, 13, 21, and 27a 27b).

However, materials under cyclic stress also undergo progressive damage, which lowers their resistance to

fracture (even at stresses below the yield strength).

Fig. 33 Cyclic stress that may lead to fatigue failure

The occurrence of fatigue (paraphrasing from Ref 28) can be generally defined as the progressive, localized,

and permanent structural change that occurs in a material subjected to repeated or fluctuating strains at nominal

stresses that have maximum values less than (and often much less than) the static yield strength of the material.

Fatigue damage is caused by the simultaneous action of cyclic stress, tensile stress, and plastic strain. If any one

of these three is not present, a fatigue crack will not initiate and propagate. The plastic strain resulting from

cyclic stress initiates the crack; the tensile stress promotes crack growth (propagation). Compressive stresses

(typically) will not cause fatigue, although compressive loads may result in local tensile stresses.

During fatigue failure in a metal free of cracklike flaws, microcracks form, coalesce, or grow to macrocracks

that propagate until the fracture toughness of the material is exceeded and final fracture occurs. Under usual

loading conditions, fatigue cracks initiate near or at singularities that lie on or just below the surface, such as

scratches, sharp changes in cross section, pits, inclusions, or embrittled grain boundaries (Ref 32).

The three major approaches of fatigue analysis and testing in current use are the stress-based (S-N curve)

approach, the strain-based approach, and the fracture mechanics approach. Both the stress-based and strain-

based approaches are based on cyclic loading of test coupons at a progressively larger number of cycles until

the test piece fractures. In stress-based fatigue testing, steels and some other alloys may exhibit a fatigue

endurance limit, which is the lower stress limit of the S-N curve for which fatigue fracture is not observed at

testing above ~10

cycles (Fig. 34). The observation of a fatigue endurance limit does not occur for all alloys

(e.g., aluminum alloy 7075 in Fig. 34), and the endurance limit can be reduced or eliminated by a number of

environmental and material factors that introduce sites for initiation of fatigue cracks. For example, Fig. 35

shows the effect of different surface conditions on the fatigue endurance limit of steels, which in this case is

approximately one-half of the tensile strength. Under these conditions, when the designs of components

subjected to cyclic loading are expected to perform under ~10

cycles, design equations such as Eq 2 and 13

would be applicable where the fatigue limit, σ

, of the material represents the failure stress, σ

. For alloys

without a fatigue endurance limit (such as aluminum alloy 7075 in Fig. 34), design stresses must be specified in

terms of the specific number of cycles expected in the lifetime of the part.

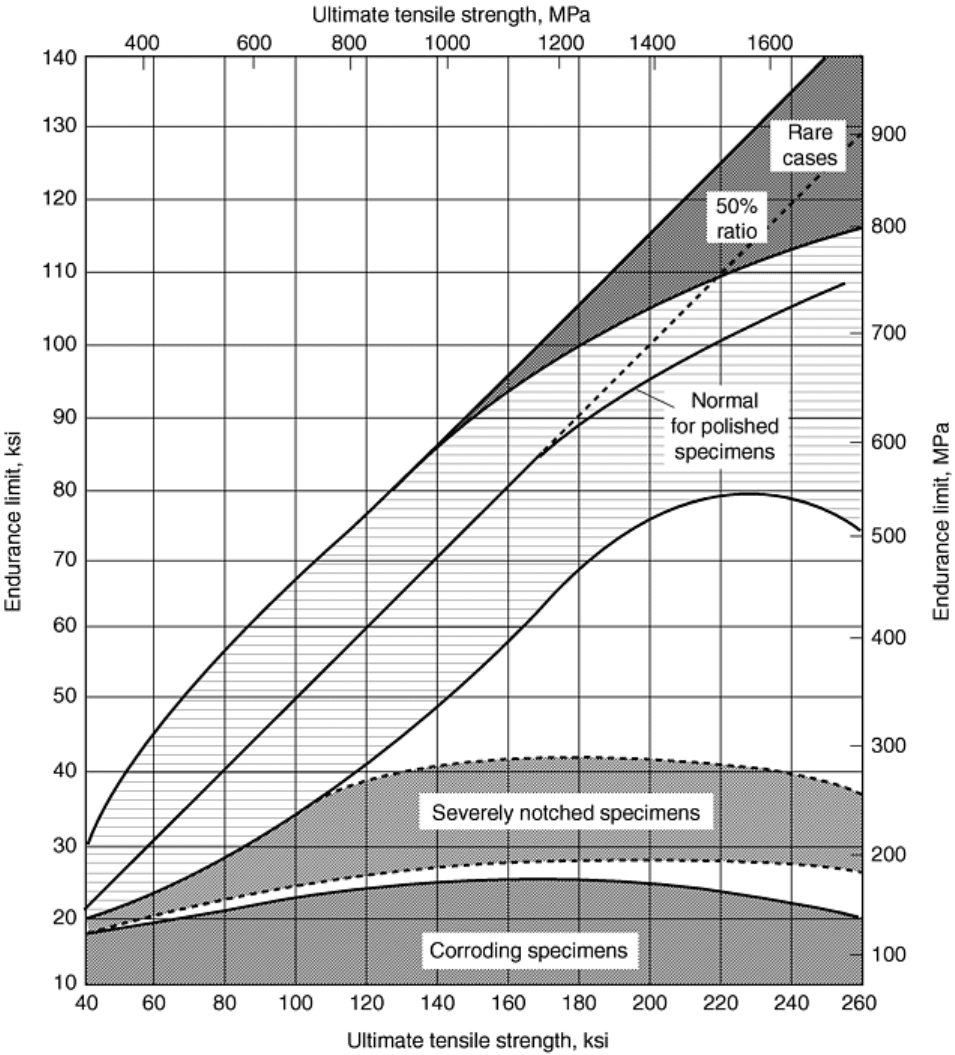
Fig. 34 Fatigue curves for ferrous and nonferrous alloys

Fig. 35 Correlation between fatigue endurance limit and tensile strength for specimens tested under

various environments

Strain-based fatigue is similar to stress-based fatigue, except that cycles to failure are measured and plotted

versus strain instead of applied stress. This type of testing and analysis is extremely useful in determining

conditions for initiation fatigue. Strain-based fatigue is used in many design cases when a major portion of total

life is exhausted in the crack initiation phase of fatigue. Fundamental design methods for this type of fatigue

analysis are described in more detail in Ref 29. Design aspects for variable amplitude and multiaxial conditions

are also described in Ref 30 and 31. Testing methods for stress-based and strain-based fatigue are described in

more detail in the article “Fatigue, Creep Fatigue, and Thermomechanical Fatigue Life Testing” in this Volume.

Although design and analysis methods based on fatigue crack initiation are important, most parts have material

flaws or geometric features that serve as sites for crack initiation. Therefore, fatigue crack growth is an integral

part of fatigue life prediction analysis. This method is based on the concepts of fracture mechanics, where