ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

(Eq 6)

where r

is the radius of the bar. Using Eq 6 to replace T

with γ

in Eq 5 and substituting in Eq 4 gives the

strain rate in the specimen as a function of strain of the reflected pulse:

(Eq 7)

When two strain gage stations are used to measure the waves on the incident bar, [

(t) -

(t)] is determined

by:

(Eq 8)

where T

, T

, and T

are the torques in the bars at gage stations A, B, and C, respectively; and t

= L

/c, t

/c, and t

= L

/c are the times required for the elastic waves in the bars to propagate the distance from the

specimen to gage stations A, B, and C, respectively. The strain rate in the specimen at time t is obtained by

using Eq 6 and substituting Eq 8 in Eq 4:

(Eq 9)

where γ

, γ

, and γ

are the strains measured at gage stations A, B, and C, respectively. The shear strain in the

specimen γ

is obtained by integrating the strain rate (given by Eq 7 or 9, depending on the configuration of

gage stations on the incident bar):

(t) =

(t)dt

(Eq 10)

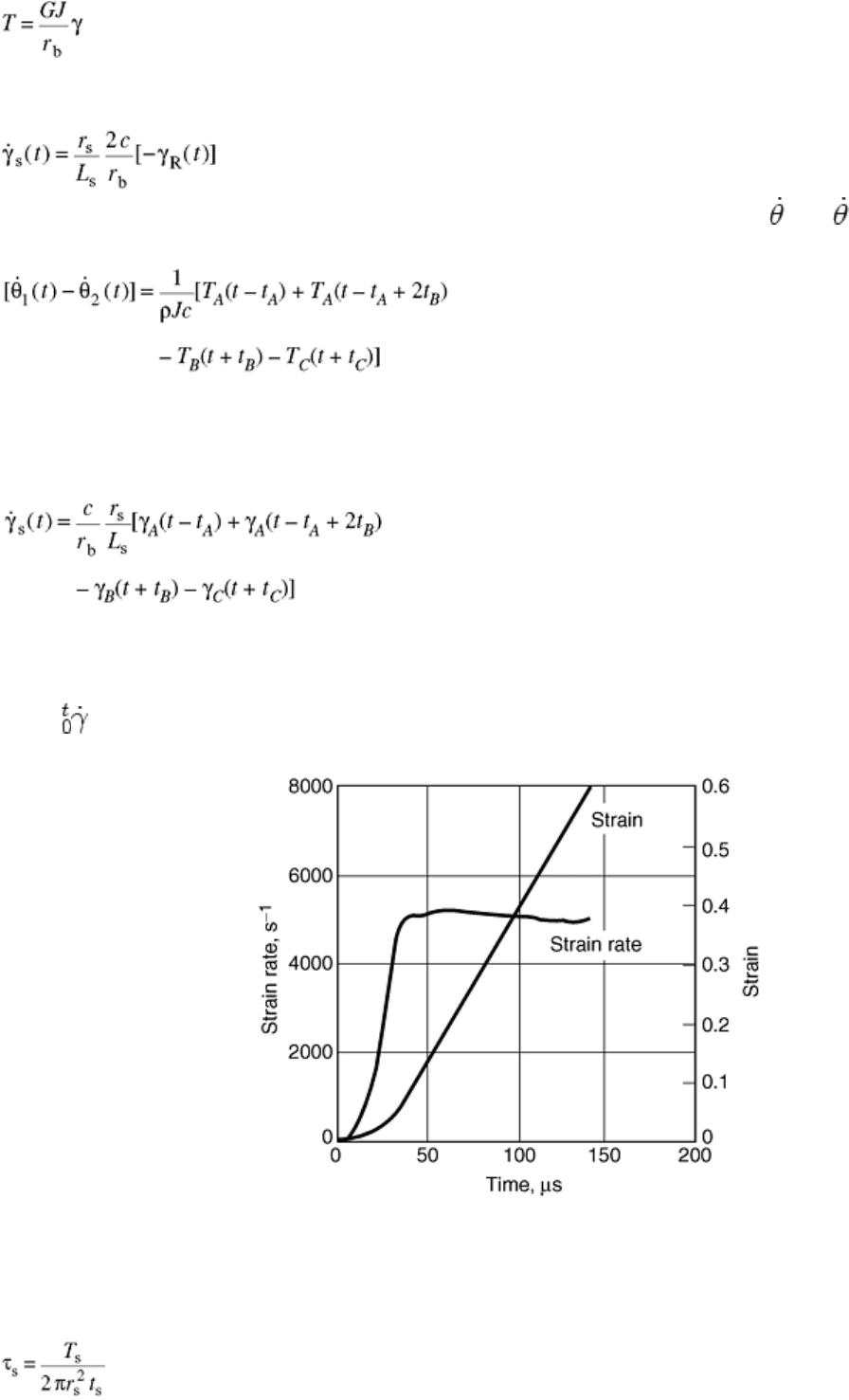
Figure 16 shows the strain rate and strain versus time calculated from the pulse records shown in Fig. 15.

Fig. 16 Strain rate in the A533B steel specimen as calculated from the pulses in Fig. 15

The shear stress in the specimen, τ

, is determined from the torque in the specimen, T

. For a thin-wall tube the

stress is given by:

(Eq 11)

where t

is the wall thickness. Because the stress in the specimen is assumed to be uniform, the torque at each

end of the specimen is the same, and the torque of the pulse transmitted to the output bar is the torque in the

specimen. In terms of the strain measured by the strain gage station on the output bar, the shear stress in the

specimen at time t is given by:

(Eq 12)

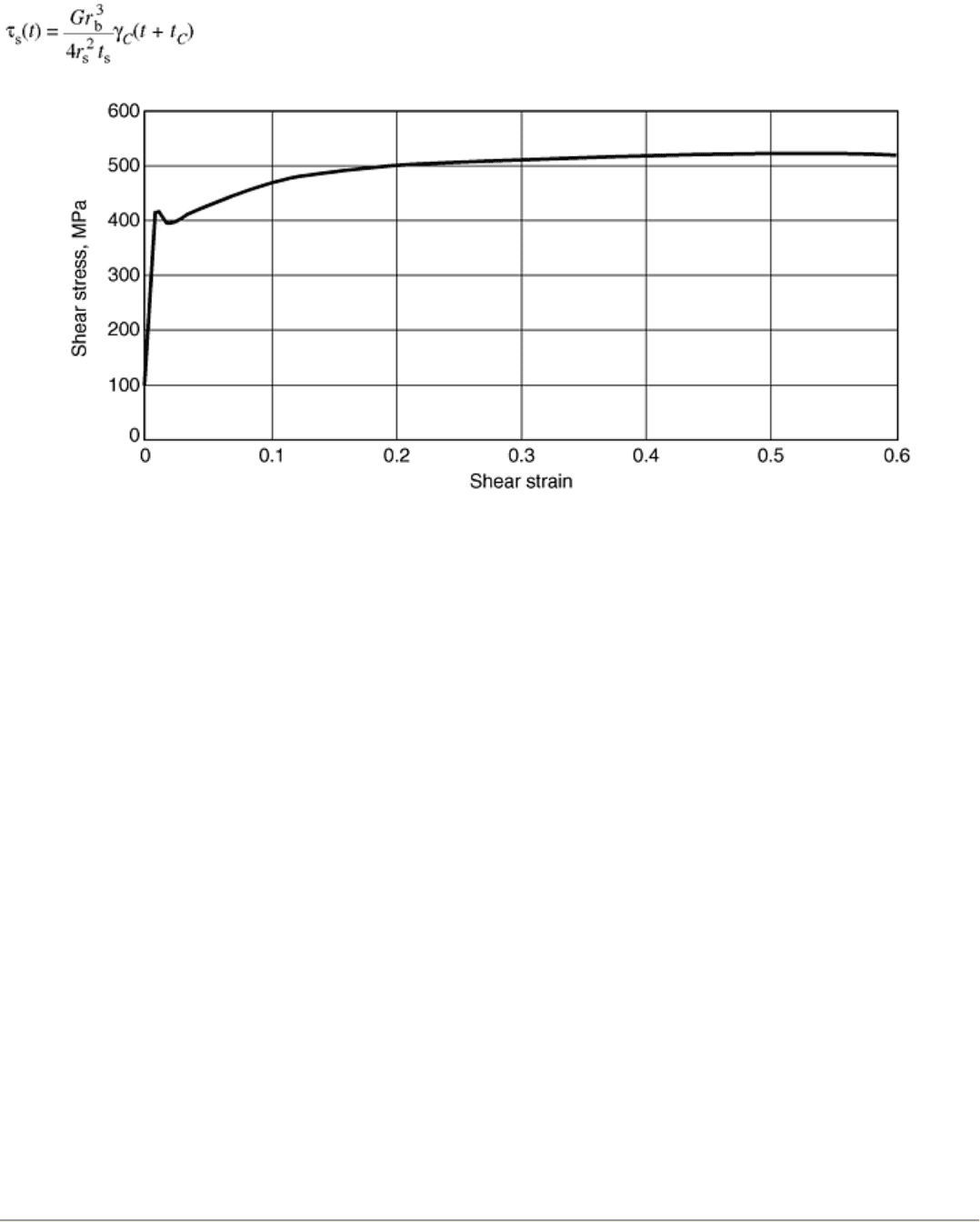
Figure 17 shows the stress-strain curve that is obtained from the records in Fig. 15 and 16.

Fig. 17 Stress-strain curve for A533B steel obtained from the records in Fig. 15 and 16. Test

temperature, 25 °C (77 °F); strain rate, 5000 s

-1

Data Recording. The signals from the Wheatstone bridges are typically recorded by a digital oscilloscope with a

frequency response of at least 1 MHz. The signals can then be processed with the oscilloscope to determine the

strain rate, strain, and strain in the specimen. Alternatively, the digitized signals can be transferred for

processing and plotting to a computer. With the availability of fast data-acquisition boards for personal

computers, recording and processing can be also done by a computer directly.

References cited in this section

14. L.S. Costin, E.E. Crisman, R.H. Hawley, and J. Duffy, On the Localization of Plastic Flow in Mild Steel

Tubes Under Dynamic Torsional Loading, in Proc. 2nd Int. Conf. Mechanical Properties of Materials

at High Rates of Strain, J. Harding, Ed., The Institute of Physics, 1979, p 287–282

18. K.A. Hartley, J. Duffy, and R.H. Hawley, The Torsional Kolsky (Split-Hopkinson) Bar, Mechanical

Testing, Vol 8, ASM Handbook, ASM International, 1985, p 218–228

19. E.K.C. Leung, An Elastic-Plastic Stress Analysis of the Specimen Used in the Torsional Kolsky Bar, J.

Appl. Mech., Vol 47, 1980, p 278–282

20. C.Y. Chiem and J. Duffy, Strain Rate History Effects and Observations of Dislocation Substructure in

Aluminum Single Crystals Following Dynamic Deformation, Mater. Sci. Eng., Vol 57, 1963, p 233–247

21. Y.H. Pao and A. Gilat, High Strain Rate Deformation and Failure of A533B Steel at Various

Temperatures, Acta Metall. Mater., Vol 40, 1992, p 1271–1280

Torsional Kolsky Bar Testing

Amos Gilat, The Ohio State University

Application Areas

Limitations on Strain Rate. The practical upper limit on the strain rate that can be achieved in tests with the

torsional Kolsky bar is about 10

-1

. This can be observed by combining Eq 4 and 5 to write the strain rate as a

function of the reflected torque, and substituting T

- T

for -T

, which gives:

(Eq 13)

where T

is the incident torque and T

is the transmitted torque. For a solid circular cylinder, the incident torque

is related to the shear stress in the incident bar (τ

) by:

(Eq 14)

Using Eq 11 and 14, the strain rate in the specimen can be obtained as:

(Eq 15)

Where τ

is the incident shear stress. From Eq 15, it is evident that the maximum strain rate is attained when the

quantity on the right side is maximized. One means is to make the specimen shorter, that is, to decrease L

However, with very short specimens, the end effects can become important; that is, the strain in the specimen

may never be uniform.

Because the second term in Eq 15 generally is small, another method of increasing the strain rate is to increase

the ratio r

by decreasing the radius of the bar, or by increasing the mean radius of the specimen. The limiting

ratio of r

that can be used is 1 because r

cannot be greater than r

without a significant change in the

impedance.

Yet another method of increasing the strain rate is to select a bar material with a high yield stress in order to

maximize τ

in Eq 15. This would appear to have an advantage because a much greater torque can be stored in

the bar. However, two other factors affect the selection of the bar material. First, the mass density, ρ, of the bar

material has to be considered. For example, the mass density of steel is about three times that of aluminum.

Thus, unless the steel has a yield stress that is more than three times that of aluminum, there will be no increase

in strain rate when using a steel bar. With this regard, a material with a high ratio of yield stress to density, such

as a titanium alloy, will theoretically maximize the strain rate. Secondly, the ability to clamp a high torque has

to be considered. As discussed earlier, it is difficult, if not impossible, to clamp a torque such that the shear

stress in the bar approaches the yield stress. High clamping pressures may also produce an axial pulse upon the

release of the clamp.

It is evident from Eq 15 that an increase in the diameter of the Kolsky bar will not increase strain rate

significantly. Increased diameter alters only the second term in Eq 15, which is considerably smaller than the

first term. From Eq 14, it is evident that, although optimum bar dimensions and material exist to achieve a

maximum strain rate, there is a physical limit of strain rate of about 10

-1

that is attainable.

The practical lower limit on strain rate in the Kolsky bar is about 10

-1

because a lower strain rate cannot be

held constant throughout the test. A constant value of strain rate requires that the magnitude of the reflected

pulse be held constant, and this in turn requires that the input pulse be considerably larger than that of the

transmitted pulse. Depending on the rate of work hardening of the specimen material, this imposes a lower limit

on the strain rate that can be attained with the Kolsky bar.

In practice, it is easiest to design a torsional Kolsky bar to reach a strain rate of about 10

-1

. This value is

easily doubled by shortening the specimen, or can be reduced by imposing less torque. Tests outside the range

of 500 to 2000 s

-1

require special consideration.

Low- and High-Temperature Testing. Theoretically, the torsional Kolsky bar technique can be used for testing

at any temperature without further modifications (other than heating or cooling) if either the whole apparatus is

at the same temperature, or only the specimen is at the testing temperature and the rest of the system is at

constant (room) temperature. Practically, it is very difficult, if not impossible, to conduct tests in either manner.

Changing the temperature of the specimen introduces a temperature gradient in the incident and transmitter

bars. Such gradients produce a variation in the shear modulus of the bars and, hence, variations in the

impedance. An impedance that is not constant along the bars causes reflections of the elastic waves that make

interpretation of the recorded wave data very difficult.

In tests below room temperature, or at mildly elevated temperatures of up to about 200 °C (392 °F), a possible

change in the elastic constants along the bars, due to temperature gradient caused by the heating or cooling of

the specimen, is small and can be neglected.

For testing at higher temperatures, various methods have been introduced. They can be divided into two

categories. One approach is to allow and monitor temperature gradients in the bars and correct for their effects.

Using this approach, Chiddister and Malvern corrected for this effect, in tests with a compression Kolsky bar,

through a calculation of the repeated partial reflections as the pulse propagated along the bar in the heat-

affected zone (Ref 22). Although this approach is acceptable, the calculations can be cumbersome. This method

can be adapted to the torsional configuration. A different solution was proposed by Eleiche and Duffy, who

tapered the Kolsky bars to counteract the effect of the thermal gradients (Ref 12). In this approach, the taper in

the Kolsky bar, which provides a variable impedance, is determined by calculation to counteract the change in

the impedance due to the temperature gradient, resulting in a constant impedance. An example of a tapered bar

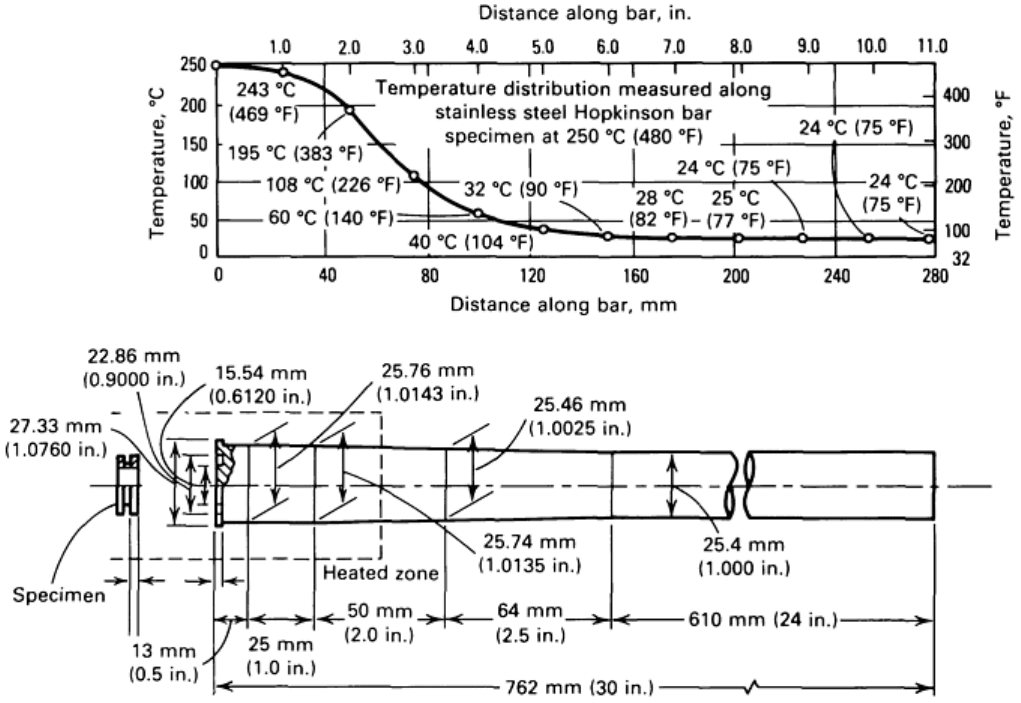
used for tests conducted at 250 °C (482 °F) is shown in Fig. 18. The disadvantage of this method is that it

requires a temperature survey before testing so that the Kolsky bar can be machined to the right taper.

Furthermore, a bar tapered for testing at one temperature cannot be used for testing at a different temperature.

The advantage of this method is that the data recorded at the strain gage stations requires no further

interpretation beyond the usual treatment for room-temperature tests. Results for 1020 steel, obtained at a

variety of temperatures at a dynamic strain rate of 10

-1

, are shown in Fig. 19.

Fig. 18 Tapered steel torsional Kolsky bar for test at 250 °C (482 °F). Source: Ref 12

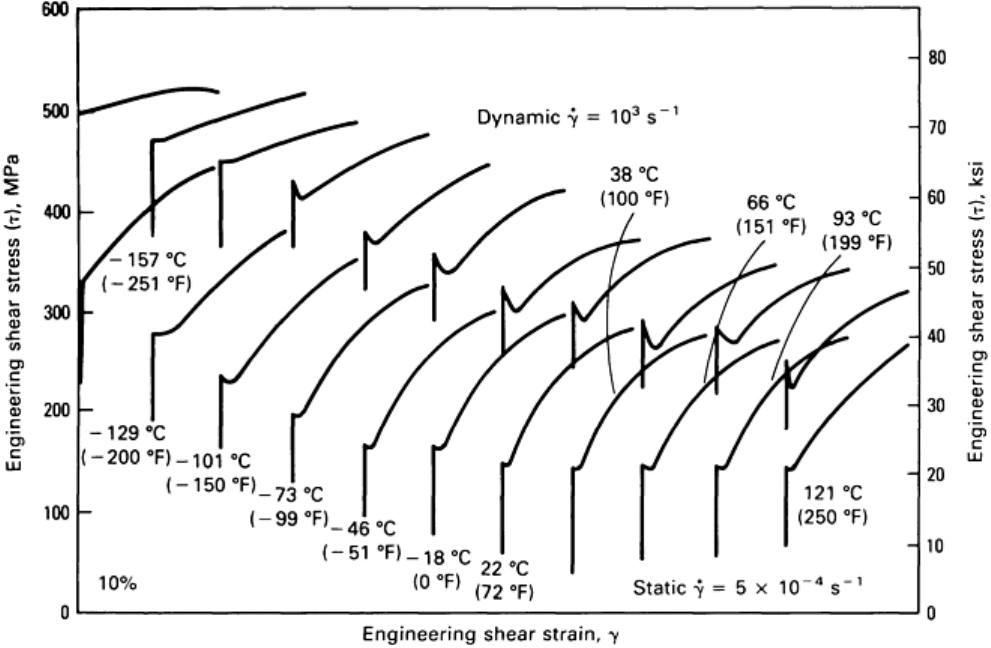
Fig. 19 Static and dynamic shear stress-strain curves at various temperatures for 1020 hot-rolled steel

Another approach is to heat the specimen and minimize the temperature increase and the length of the affected

regions of the bars. This approach was used by Gilat and Wu for tests at temperatures up to 1060 °C (1940 °F)

(Ref 13). They used a rapid-heating device and a connection between the specimen and the bars that allows

transmission of the torsional wave with constant impedance and minimizes heat conduction to the bars. The

heat-affected zone was only 20 mm (0.79 in.) long and did not have a noticeable effect on the propagating

pulses. This allows recording and processing of the data in the same manner as in room-temperature tests. In a

similar method, inserts, made of a material with elastic constants that are not affected significantly by

temperature of the magnitude used in the test, are placed between the specimen and the bars (Ref 23). The

specimen and the adjacent ends of the inserts are heated to the testing temperature while the temperature

gradient is confined to the inserts.

Quasi-Static and Incremental Strain-Rate Testing. Specimens can also be tested in torsion quasi-statically using

a stored-torque Kolsky bar, as shown schematically in Fig. 20. In this case, the incident bar is clamped against

rotation as in the dynamic test, but quasi-static loading is applied by a pulley system at the far end of the

transmitter bar by means of a variable-drive low-speed electric motor.

Fig. 20 Schematic of a stored-torque torsional Kolsky bar modified for quasi-static and incremental

strain rate tests. DCDT, direct current differential transformer

The stress during the quasi-static loading is measured, as in the dynamic test, by a four-arm bridge on the

transmitter bar. To determine the strain in the specimen, two linear direct-current differential transformers are

placed equidistant from the specimen. Extremely fine wires attached to the cores of the differential transformers

are wound around the bars. As the bars rotate, the cores are pulled vertically out of the transformer coils. The

difference between the output signals from the direct-current differential transformers is directly proportional to

the amount of twist undergone by the specimen plus the elastic twist of the portion of the Kolsky bar between

the differential transformers. To obtain the shear strain in the specimen, the elastic rotation of the bar between

the two differential transformers is subtracted from the total rotation. The elastic rotation is measured by

cementing the bars together without a specimen and loading them quasi-statically. Results for 1020 steel

obtained at a variety of temperatures at a quasi-static strain rate of 5 × 10

-4

-1

are included in Fig. 19.

In incremental strain-rate testing, the incident bar is clamped and a torque for the dynamic test is stored. Then, a

quasi-static loading is applied by a pulley system at the far end of the transmitter bar. When the strain in the

specimen reaches the predetermined value, the clamp is released and the specimen is dynamically loaded (Ref

8, 9).

Constant strain-rate tests and incremental strain-rate tests can be used for determining the apparent and true

strain-rate sensitivity. The apparent strain-rate sensitivity, μ

, is defined by:

(Eq 16)

where Δτ, as shown in Fig. 21, is the difference in flow stress between two constant strain-rate curves at

and

. Experiments are performed at various constant strain rates, and the stress (at a given value of strain) is

plotted as a function of strain rate on a logarithmic scale. The slope of this line provides the value of the

derivative in Eq 16.

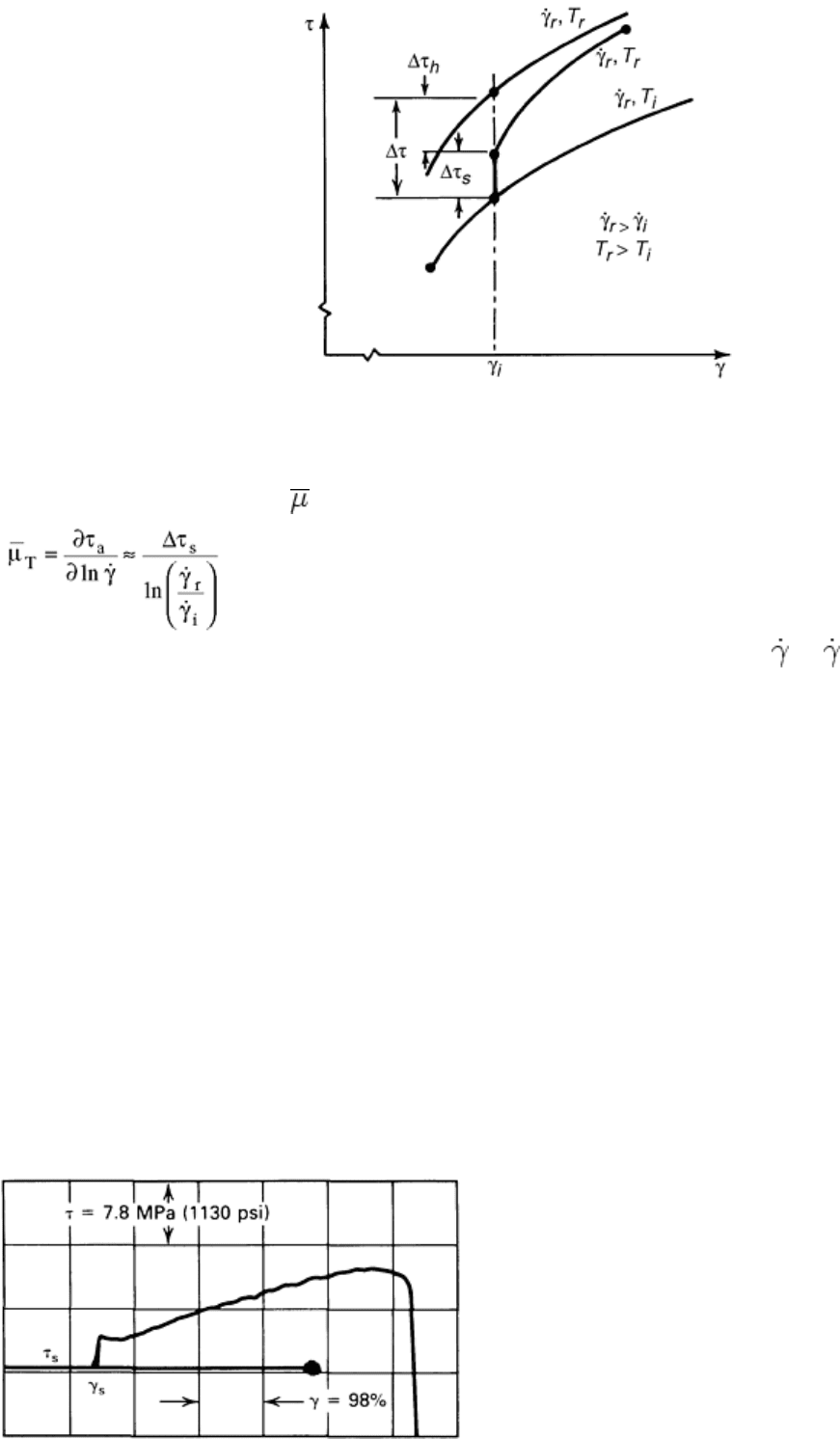
Fig. 21 Schematic representation of the effect of rapid changes in strain rate on flow stress for face-

centered-cubic metals

The true strain-rate sensitivity,

, is defined by:

(Eq 17)

where Δτ

is the difference in flow stress due to an increment in strain rate from

. The true strain-rate

sensitivity is determined from the incremental strain-rate test. Figure 21 illustrates a typical stress-strain curve

obtained in such a test. As shown, the flow stress after the strain-rate increment is different from the flow stress

at the same value of strain in a specimen strained entirely at the dynamic strain rate. This leads to a difference

between the apparent and true strain-rate sensitivities. For face-centered-cubic (fcc) and hexagonal-close-

packed (hcp) metals, the all-dynamic flow stress is greater than the flow stress immediately after the increment

in strain rate. This difference is commonly referred to as the strain-rate history effect because in both cases the

strain is the same, but the history of strain rate is different (Ref 8, 9, and 24).

Frequently, with further deformation, the difference between the two values of flow stress diminishes, and

eventually the two dynamic curves merge. In this case, the material is said to have a “fading memory” (Ref 25).

Body-centered cubic metals, under certain conditions and particularly at very low temperatures, may exhibit a

negative strain-rate history effect; that is, the flow stress after an increment in strain rate is greater than the flow

stress for the material strained entirely at the dynamic rate (Ref 26). At room temperature, bcc metals generally

show only a small history effect, although the influence of strain rate on flow stress usually is considerably

greater than that for fcc metals.

In incremental strain rate tests, the Kolsky bar provides an important advantage: the transmitted signal furnishes

a measure not of the total stress in the specimen, but of the excess stress, Δτ

, imposed by the stress pulse above

the existing stress as a result of loading at the quasi-static strain rate (Fig. 22). Thus, rather than evaluation of a

small difference between two large numbers, measurement of the stress increment, Δτ

, can be made directly

from oscilloscope records. Results of incremental strain-rate tests on aluminum are shown in Fig. 23.

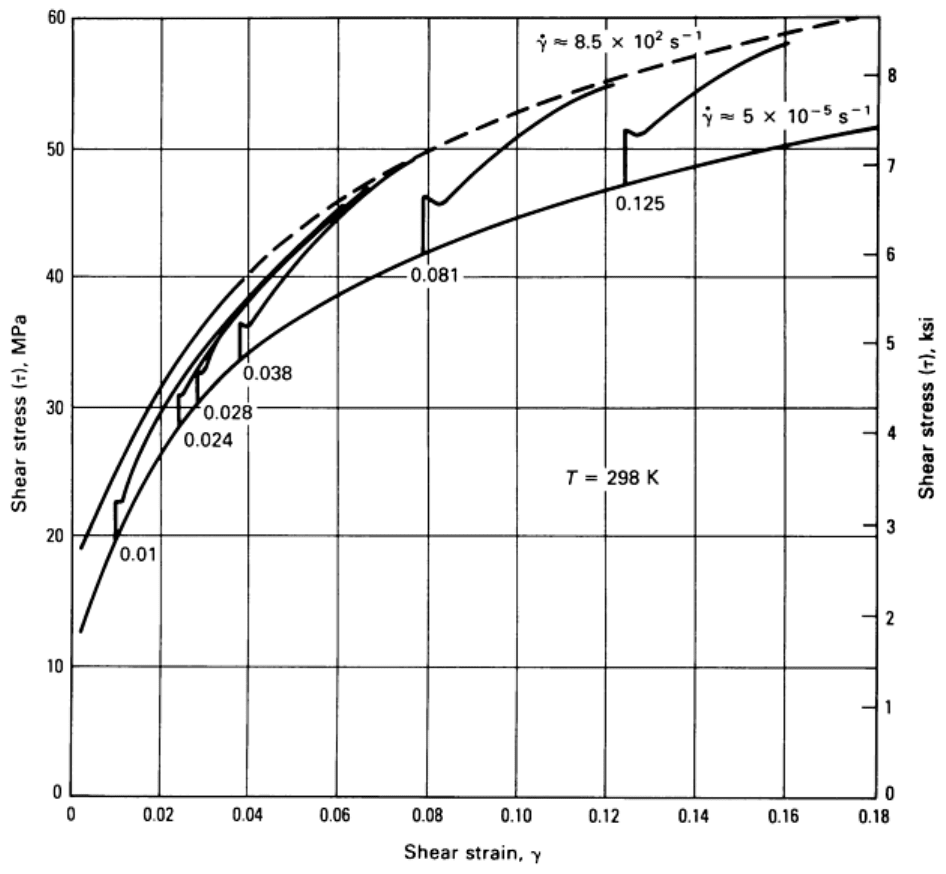
Fig. 22 Oscilloscope record of dynamic portion of incremental strain-rate test. Vertical deflection

represents excess stress over τ

the maximum static stress. Horizontal deflection represents excess strain

over γ

Fig. 23 Behavior of 1100-O aluminum under static, dynamic, and incremental strain-rate loading in

shear. Strain rate changes form 5 × 10

-5

to 850 s

-1

in incremental rate test. Source: Ref 8

Localization and Shear-Banding Experiments. The torsional Kolsky bar has been used for studying localization

of plastic deformation and the formation of adiabatic shear bands (Ref 14, 15, and 16). As already mentioned,

the existence of localized deformation is evident when a scribed line along the gage length of the specimen

appears to be discontinuous after the test (Fig. 11). A detailed study of the evolution of the localization is done

by taking high-speed photographs of deforming grid lines on the specimen (Ref 15, 16). Strain profiles,

obtained by analyzing the deformed grid at different times along the specimen gage length, are shown in Fig.

24. Attempts have also been made to measure the increase in temperature at the shear band during the

deformation process (Ref 15). This was done by measuring the infrared radiation emitted from the surface of

the specimen.

Fig. 24 Shear strain profiles across the specimen width during the formation of adiabatic shear band.

Source: Ref 16

Recently, a recovery experiment, in which the specimen is loaded up to a predetermined strain and then

unloaded and recovered for microscopic examination, has also been introduced (Ref 17). In a standard test, the

actual material testing takes place during loading by the first wave that arrives to the specimen. The transmitted

and reflected waves, however, are reflected back toward the specimen from the far ends of the bars and

continue to reverberate in the system. If the specimen does not break during the first loading, it is subjected to

further loading as the waves reflect back and forth. Consequently, when the specimen is removed after the test,

its microstructure cannot be related to the deformation that took place during the initial loading.

In a recovery experiment, the specimen is loaded only once, which means that after the test the specimen can be

removed and examined. In Ref 17, reloading of the specimen by the reflected transmitted pulse is eliminated by

trapping the wave. Reloading by a reflection of the incident wave is avoided by designing the test so that the

amplitude of the reflected wave is reduced to a level below the elastic limit. Recovery experiments are simpler

to conduct with the compression version of the Kolsky bar.

References cited in this section

8. R.A. Frantz and J. Duffy, The Dynamic Stress-Strain Behavior in Torsion of 1100-O Aluminum

Subjected to a Sharp Increase in Strain Rate, J. Appl. Mech., Vol 39, 1972, p 939–945

9. J.D. Campbell, A.M. Eleiche, and M.C.C. Tsao, Strength of Metals and Alloys at High Strains and

Strain Rates, in Fundamental Aspects of Structural Alloy Design, R.J. Jaffee and B.A. Wilcox, Ed.,

Plenum Press, 1977, p 545–563

12. A.M. Eleiche and J. Duffy, Effects of Temperature on the Static and Dynamic Stress-Strain

Characteristics in Torsion of 1100-O Aluminum, Int. J. Mech. Sci., Vol 17, 1975, p 85–95

13. A. Gilat and X. Wu, Elevated Temperature Testing with the Torsional Split Hopkinson Bar, Exp. Mech.,

Vol 34 (No. 2), 1994, p 166–170

14. L.S. Costin, E.E. Crisman, R.H. Hawley, and J. Duffy, On the Localization of Plastic Flow in Mild Steel

Tubes Under Dynamic Torsional Loading, in Proc. 2nd Int. Conf. Mechanical Properties of Materials

at High Rates of Strain, J. Harding, Ed., The Institute of Physics, 1979, p 287–282

15. A. Marchand and J. Duffy, An Experimental Study of the Formation Process of Adiabatic Shear Bands

in a Structural Steel, J. Mech. Phys. Solids, Vol 36, 1988, p 251–283

16. J.H. Giovanola, Adiabatic Shear Banding Under Pure Shear Loading, Part I: Direct Observation of

Strain Localization and Energy Dissipation Measurements, Mech. Mater., Vol 7, 1988, p 59–71

17. Q. Xue, L.T. Shen, and Y.L. Bai, A Modified Split Hopkinson Torsional Bar in Studying Shear

Localization, Meas. Sci. Technol., Vol 6, 1995, p 1557–1565

22. J.L. Chiddister and L.E. Malvern, Compression Impact Testing Of Aluminum at Elevated Temperatures,

Exp. Mech., Vol 3, 1963, p 81–90

23. C.G. Schmidt, R.D. Caligiuri, J.H. Giovanola, and D.C. Erlich, Effect of Grain Size on High Strain Rate

Deformation of Copper, Metall. Trans. A, Vol 22, 1991, p 2349–2357

24. J. Duffy, Strain Rate History Effects and Dislocation Substructure at High Strain Rates, in Materials

Behavior Under High Stress and Ultrahigh Loading Rates, J. Mescall and V. Weiss, Ed., Plenum Press,

1983, p 21–37

25. J. Klepaczko, Strain-Rate History Effects for Polycrystalline Aluminum and the Theory of Intersections,

J. Mech. Phys. Solids, Vol 16, 1968, p 255–266

26. K.A. Hartley and J. Duffy, Strain Rate and Temperature History Effects During Deformation of FCC

and BCC Metals, in Mechanical Properties of Materials at High Rates of Strain, J. Harding, Ed., The

Institute of Physics, 1984, p 21–30

Torsional Kolsky Bar Testing

Amos Gilat, The Ohio State University

Acknowledgments

The present article is a revision of the article The Torsional Kolsky (Split-Hopkinson) Bar by K.A. Hartley, J.

Duffy, and R.H. Hawley, which appeared in Mechanical Testing, Vol 8, ASM Handbook, ASM International,

1985, p 218–228. Some sections and paragraphs from the original article are included here without alteration.

Torsional Kolsky Bar Testing

Amos Gilat, The Ohio State University

References

1. U.S. Lindholm, High Strain Rate Tests, in Measurement of Mechanical Properties, Vol 5, Part I,

Techniques of Metals Research, R.F. Bunshah, Ed., Interscience, 1971, p 199–271