ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

2. H. Kolsky, An Investigation of the Mechanical Properties of Materials at Very High Rates of Loading,

Proc. Phys. Soc. London, Vol 62-B, 1949, p 676–700

3. B. Hopkinson, The Effects of Momentary Stresses in Metals, Proc. Phys. Soc. London, Vol 74-A, 1905,

p 498–506

4. W.W. Baker and C.H. Yew, Strain Rate Effects in the Propagation of Torsional Plastic Waves, J. Appl.

Mech., Vol 33, 1966, p 917–923

5. J. Duffy, J.D. Campbell, and R.H. Hawley, On the Use of a Torsional Split Hopkinson Bar to Study

Rate Effects in 1100-O Aluminum, J. Appl. Mech., Vol 38, 1971, p 83–91

6. T. Nicholas and J.E. Lawson, On the Determination of the Mechanical Properties of Materials at High

Shear-Strain Rates, J. Mech. Phys. Solids, Vol 20, 1972, p 57–64

7. J.L. Lewis and J.D. Campbell, The Development and Use of a Torsional Hopkinson Bar Apparatus,

Exp. Mech., Vol 12 (No. 11), 1972, p 520–524

8. R.A. Frantz and J. Duffy, The Dynamic Stress-Strain Behavior in Torsion of 1100-O Aluminum

Subjected to a Sharp Increase in Strain Rate, J. Appl. Mech., Vol 39, 1972, p 939–945

9. J.D. Campbell, A.M. Eleiche, and M.C.C. Tsao, Strength of Metals and Alloys at High Strains and

Strain Rates, in Fundamental Aspects of Structural Alloy Design, R.J. Jaffee and B.A. Wilcox, Ed.,

Plenum Press, 1977, p 545–563

10. J. Lipkin, J.D. Campbell, and J.D. Swearengen, The Effects of Strain-Rate Variations on the Flow Stress

of OFHC Copper, J. Mech. Phys. Solids, Vol 26, 1978, p 251–268

11. A. Gilat and Y.H. Pao, High Rate Decremental-Strain Rate Test, Exp. Mech., Vol 28 (No. 3), 1988, p

322–325

12. A.M. Eleiche and J. Duffy, Effects of Temperature on the Static and Dynamic Stress-Strain

Characteristics in Torsion of 1100-O Aluminum, Int. J. Mech. Sci., Vol 17, 1975, p 85–95

13. A. Gilat and X. Wu, Elevated Temperature Testing with the Torsional Split Hopkinson Bar, Exp. Mech.,

Vol 34 (No. 2), 1994, p 166–170

14. L.S. Costin, E.E. Crisman, R.H. Hawley, and J. Duffy, On the Localization of Plastic Flow in Mild Steel

Tubes Under Dynamic Torsional Loading, in Proc. 2nd Int. Conf. Mechanical Properties of Materials

at High Rates of Strain, J. Harding, Ed., The Institute of Physics, 1979, p 287–282

15. A. Marchand and J. Duffy, An Experimental Study of the Formation Process of Adiabatic Shear Bands

in a Structural Steel, J. Mech. Phys. Solids, Vol 36, 1988, p 251–283

16. J.H. Giovanola, Adiabatic Shear Banding Under Pure Shear Loading, Part I: Direct Observation of

Strain Localization and Energy Dissipation Measurements, Mech. Mater., Vol 7, 1988, p 59–71

17. Q. Xue, L.T. Shen, and Y.L. Bai, A Modified Split Hopkinson Torsional Bar in Studying Shear

Localization, Meas. Sci. Technol., Vol 6, 1995, p 1557–1565

18. K.A. Hartley, J. Duffy, and R.H. Hawley, The Torsional Kolsky (Split-Hopkinson) Bar, Mechanical

Testing, Vol 8, ASM Handbook, ASM International, 1985, p 218–228

19. E.K.C. Leung, An Elastic-Plastic Stress Analysis of the Specimen Used in the Torsional Kolsky Bar, J.

Appl. Mech., Vol 47, 1980, p 278–282

20. C.Y. Chiem and J. Duffy, Strain Rate History Effects and Observations of Dislocation Substructure in

Aluminum Single Crystals Following Dynamic Deformation, Mater. Sci. Eng., Vol 57, 1963, p 233–247

21. Y.H. Pao and A. Gilat, High Strain Rate Deformation and Failure of A533B Steel at Various

Temperatures, Acta Metall. Mater., Vol 40, 1992, p 1271–1280

22. J.L. Chiddister and L.E. Malvern, Compression Impact Testing Of Aluminum at Elevated Temperatures,

Exp. Mech., Vol 3, 1963, p 81–90

23. C.G. Schmidt, R.D. Caligiuri, J.H. Giovanola, and D.C. Erlich, Effect of Grain Size on High Strain Rate

Deformation of Copper, Metall. Trans. A, Vol 22, 1991, p 2349–2357

24. J. Duffy, Strain Rate History Effects and Dislocation Substructure at High Strain Rates, in Materials

Behavior Under High Stress and Ultrahigh Loading Rates, J. Mescall and V. Weiss, Ed., Plenum Press,

1983, p 21–37

25. J. Klepaczko, Strain-Rate History Effects for Polycrystalline Aluminum and the Theory of Intersections,

J. Mech. Phys. Solids, Vol 16, 1968, p 255–266

26. K.A. Hartley and J. Duffy, Strain Rate and Temperature History Effects During Deformation of FCC

and BCC Metals, in Mechanical Properties of Materials at High Rates of Strain, J. Harding, Ed., The

Institute of Physics, 1984, p 21–30

Triaxial Hopkinson Techniques

Sia Nemat-Nasser, Jon Isaacs, and Jacob Rome, University of California, San Diego

Introduction

COMPRESSIVE PROPERTIES AND FAILURE MODES of many materials, particularly brittle materials, are

dramatically affected by stress triaxiality. This has been demonstrated through various laboratory experiments,

since the early work of Bridgman (Ref 1), who demonstrated several failure modes peculiar to high pressures,

leading to paradoxical results. The common feature of these paradoxes is that failure always occurs by the

formation of tension cracks in specimens subjected to pure compression. While all these paradoxes have been

fully understood (Ref 2), they do emphasize the importance of controlled triaxial experiments in materials

characterization. Indeed, in axial compression, brittle materials such as rocks or ceramics fail by axial splitting,

faulting, or plastic deformation (barreling), depending on the relative magnitude of the confining pressure that

may accompany the axial compression (Ref 3, 4, 5, and 6). Model studies show that similar results emerge at

high strain rate.

Triaxial Hopkinson techniques can be used to simultaneously subject a sample to axial and lateral

compressions. The lateral compression may be applied through a pneumatic pressure vessel (Ref 7, 8, and 9) or

dynamically using a special Hopkinson technique. These two techniques are reviewed in this article.

References cited in this section

1. P.W. Bridgman, The Physics of High Pressure, Bell, London, 1931

2. C.H. Scholtz, G. Boitnott, and S. Nemat-Nasser, The Bridgman Ring Paradox Revisited, Pure and

Applied Geophysics (PAGEOPH), Vol 124, 1986, p 587–599

3. S. Nemat-Nasser and H. Horii, Compression-Induced Nonplanar Crack Extension with Application to

Splitting, Exfoliation, and Rockburst, J. Geophys. Res., Vol 87 (No. B8), 1982, p 6805–6821

4. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery

Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391

5. H. Horii and S. Nemat-Nasser, Compression-Induced Microcrack Growth in Brittle Solids: Axial

Splitting and Shear Failure, J. Geophys. Res., Vol 90 (No. B4), 1985, p 3105–3125

6. H. Horii and S. Nemat-Nasser, Brittle Failure in Compression: Splitting, Faulting and Brittle-Ductile

Transition, Philos. Trans. R. Soc. (London) A, Vol 319 (No. 1549), 1986, p 337–374

7. R.J. Christensen, S.R. Swanson, and W.S. Brown, Split Hopkinson Bar Test on Rock under Confining

Pressure, Exp. Mech., Vol 12, 1972, p 508–541

8. L.E. Malvern, D.A. Jenkins, T. Tang, and S. McClure, Dynamic Testing of Laterally Confined

Concrete, Micromechanics of Failure of Quasi Brittle Materials, Elsevier Applied Science, 1991, p

343–352

9. G. Gary and B. Bailly, Behaviour of Quasi-Brittle Material at High Strain Rate, Experiment and

Modelling, Eur. J. Mech., A/Solids, Vol 17 (No. 3), 1998, p 403–420

Triaxial Hopkinson Techniques

Sia Nemat-Nasser, Jon Isaacs, and Jacob Rome, University of California, San Diego

Pneumatic Pressure Vessel

Figures 1 and 2 are a photograph and a schematic, respectively, of a 75 mm (3 in.) Hopkinson system,

particularly designed to test large samples of concrete, rock, polymeric composites, and other materials with

relatively course microstructures. Except for a 6 ft brake bar to absorb the momentum and dissipate the energy,

the system is similar to the classical Hopkinson bar discussed in the article “Classic Split-Hopkinson Pressure

Bar Testing” in this section. The brake bar acts as a simple friction brake. Two clamps are secured around the

brake bar, and the tightness is adjusted to ensure that the brake bar absorbs the energy efficiently.

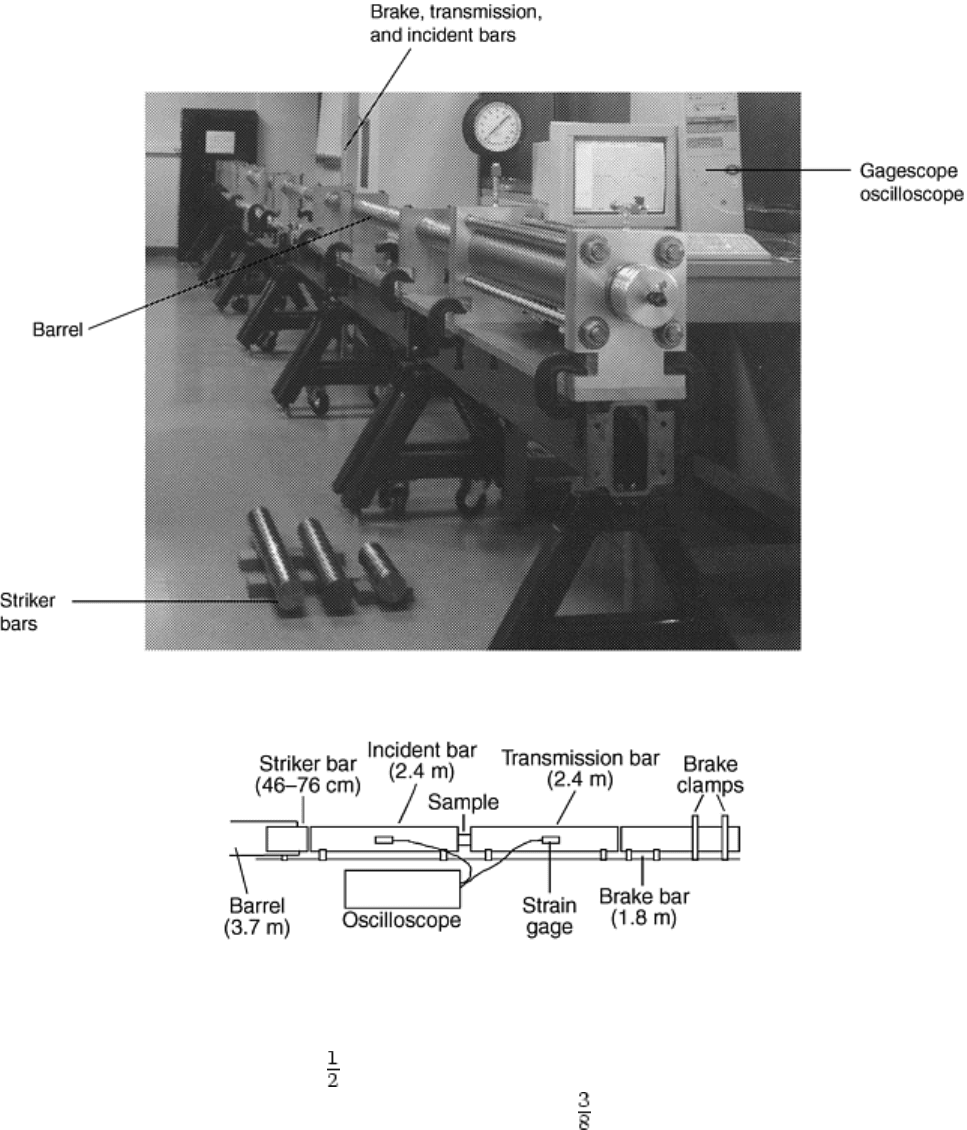
Fig. 1 Photograph of a 75 mm (3 in.) diam Hopkinson bar test system

Fig. 2 Schematic of a 75 mm (3 in.) diam Hopkinson bar test system

A large diameter pressure vessel provides the pneumatic confinement (Fig. 3, 4). A steel cylinder of 150 mm (6

in.) outside diameter (OD) and 13 mm ( in.) wall thickness surrounds the sample. The aluminum end plates are

each 25 mm (1 in.) thick and are held together by four 9.5 mm ( in.) bolts. A rubber sleeve, secured by hose

clamps, is placed over the sample to prevent direct contact between the sample and the high-pressure gas. O-

rings are used to seal the pressurized chamber. A band clamp and the brake bar restrain the incident and

transmission bars, respectively, to prevent them from moving apart. This pressure vessel provides a constant

radial confinement of up to 7 MPa (1000 psi).

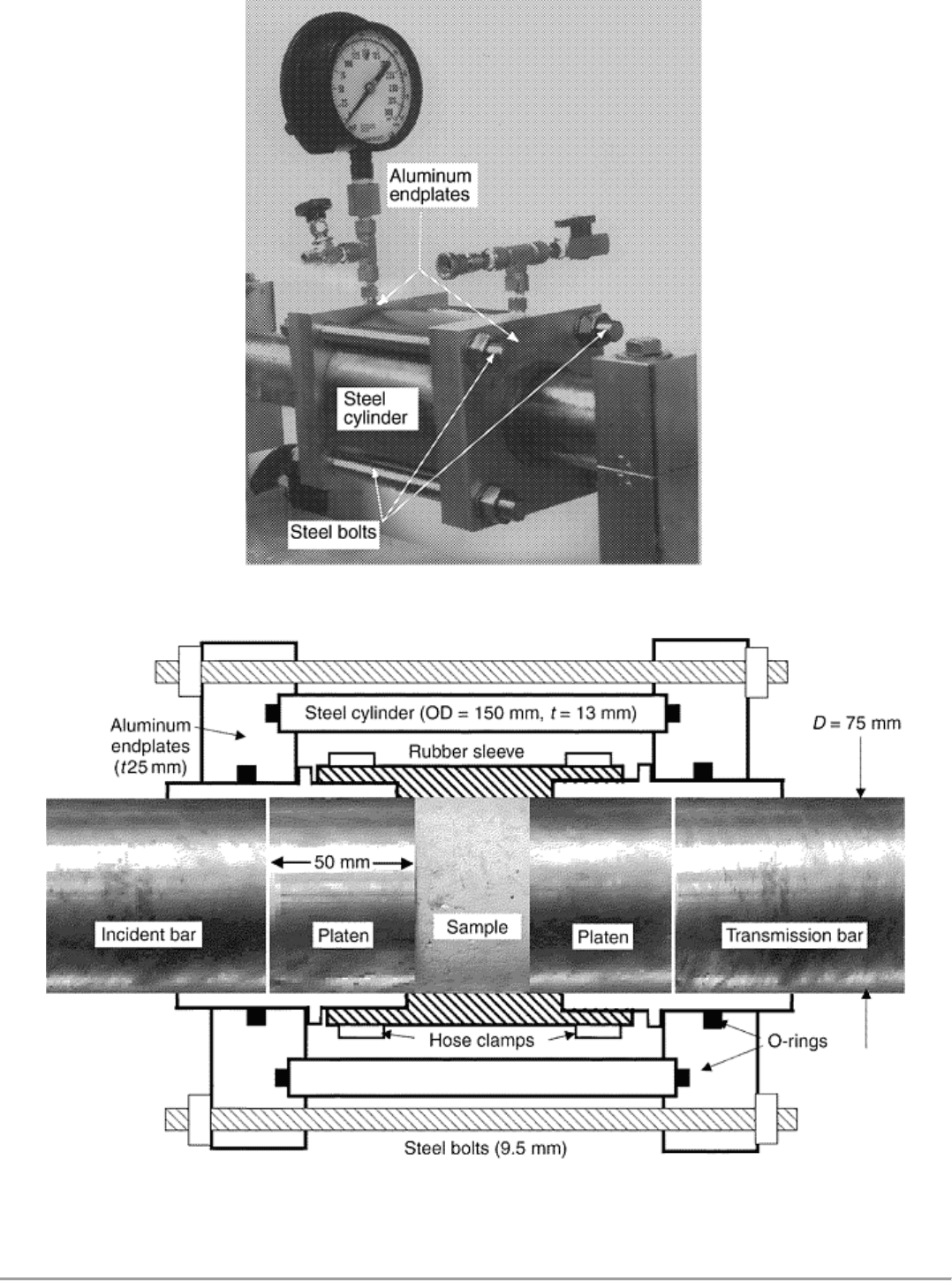
Fig. 3 Photograph of a pneumatic pressure vessel for a 75 mm (3 in.) Hopkinson bar test system

Fig. 4 Schematic of a pneumatic pressure vessel for a 75 mm (3 in.) Hopkinson bar test system. t,

thickness; D, diameter; OD, outside diameter

Triaxial Hopkinson Techniques

Sia Nemat-Nasser, Jon Isaacs, and Jacob Rome, University of California, San Diego

Dynamic Confinement

The classical Hopkinson Bar can be modified to allow dynamic triaxial compressive loading of a sample. This

technique simultaneously loads the sample in the axial and radial directions. Figures 5 and 6 are a photograph

and schematic, respectively, of this system. The striker (A) impacts the first incident bar (B), generating the

incident pulse. The wave is transmitted to the second incident bar (C) and the incident tube (F). (Note: With this

design, the reflected pulse cannot be measured directly, so it is calculated as the difference between the

transmitted pulse and the incident pulse.) The sample (D) is inside a Teflon (E.I. DuPont de Nemours & Co.,

Inc., Wilmington, DE) tube (G), which in turn is inside an aluminum sleeve (H).

Fig. 5 Close-up photograph of dynamic triaxial load cell on a 19 mm ( in.) Hopkinson bar

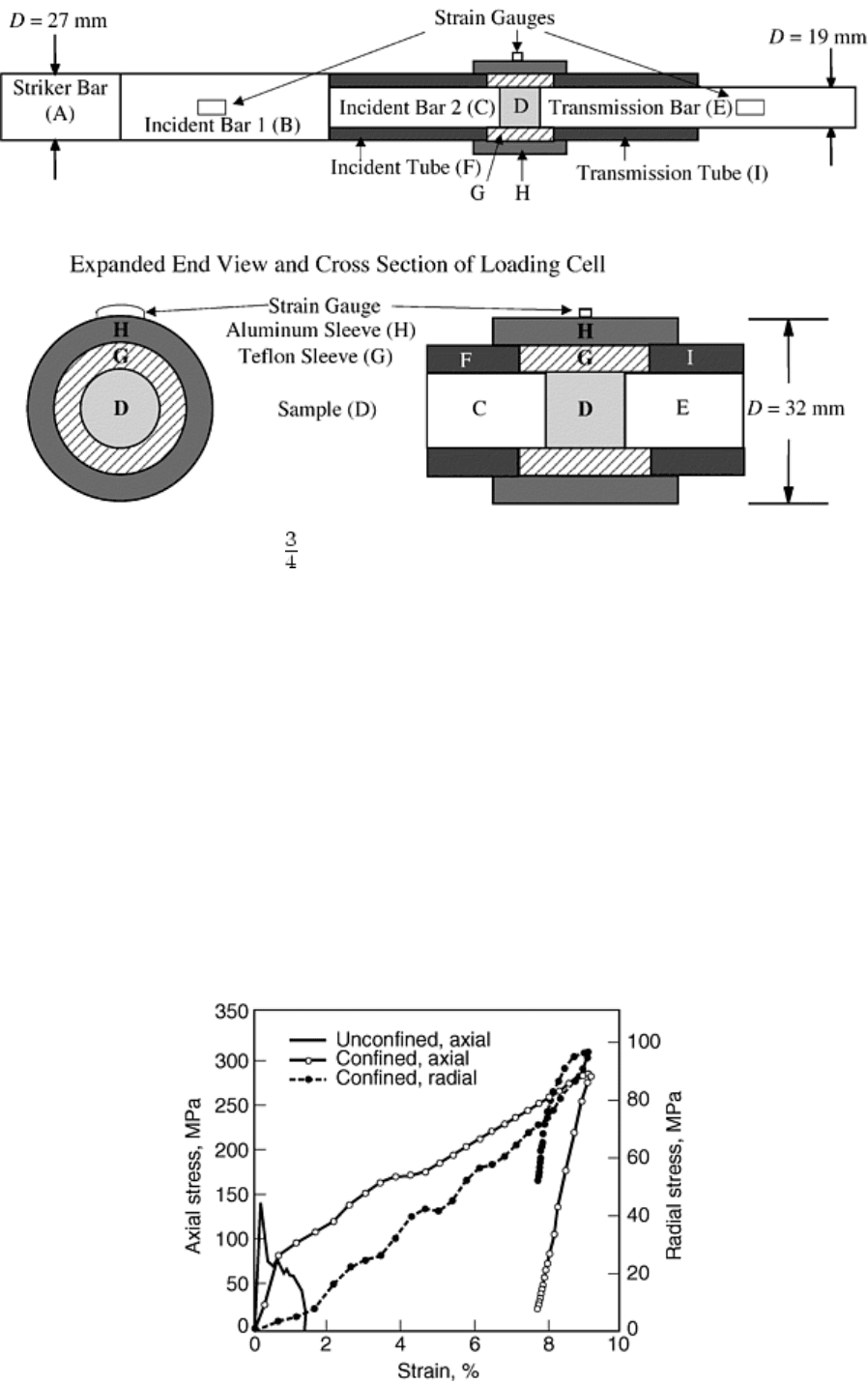
Fig. 6 Schematic of a 19 mm ( in.) Hopkinson bar featuring the dynamic triaxial load cell

The confinement is provided by the Teflon, which is dynamically compressed between the incident tube (F) and

the transmission tube (I). Restrained laterally by the aluminum sleeve, a large hydrostatic stress is produced in

the Teflon. This pressure creates a large radial stress on the sample. The hoop strain in the aluminum sleeve is

measured, and the radial confining stress is calculated. The radial stress can be controlled independently from

the axial stress and strain to a limited extent by, for example, altering the thickness of the aluminum sleeve to

control when the sleeve yields.

The simultaneous loading in the radial and axial directions is ensured by the design of the bar. The stress waves

in the incident bar and the incident tube are generated at the same time. The bar and the tube are made of the

same material and they have nearly the same length. Thus, the stress wave in the incident bar reaches the

sample (loading it axially) at the same time as the stress wave in the incident tube reaches the Teflon (loading

the sample radially).

This method has been used to test several samples. In Fig. 7, the response of a mortar sample tested in uniaxial

compression is compared with another mortar sample tested in triaxial compression. These results demonstrate

both the effect radial confinement can have on a brittle material and the simultaneous loading of the sample in

the axial and radial directions.

Fig. 7 Response of mortar tested under uniaxial and triaxial compression at about 500 s

-1

on a 19 mm (

in.) Hopkinson bar

Triaxial Hopkinson Techniques

Sia Nemat-Nasser, Jon Isaacs, and Jacob Rome, University of California, San Diego

References