ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation
Подождите немного. Документ загружается.

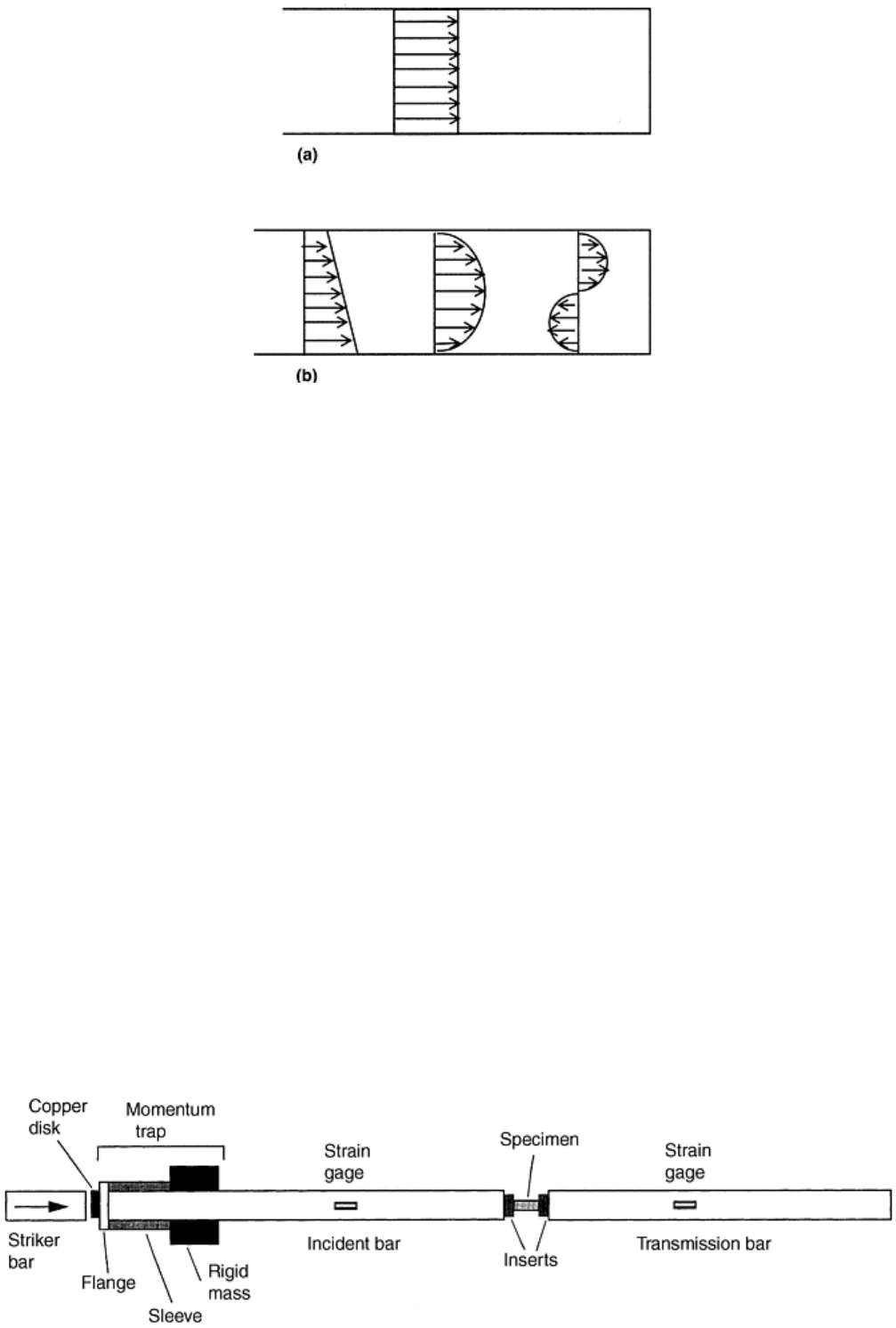
Fig. 5 Examples of (a) uniform stress and (b) nonuniform stress distribution in split-Hopkinson pressure
bar testing
The fifth assumption (that the accumulated strain in the specimen is due solely to a single incident compression
pulse reaching the specimen) emphasizes the fact that in traditional SHPB testing, a ceramic specimen is
subjected to repeated loading (due to wave reflections within the incident bar) unless it is fractured during the
first compression pulse loading. In the traditional design, shown in Fig. 1, the reflected pulse off the specimen
is tensile in nature, and when it reaches the striker end of the incident bar, A, it reflects back as a compression
pulse and travels once again toward the specimen, thus reloading the specimen. This process repeats several
times causing multiple loadings on the specimen. Notice that the stress-strain response obtained from the initial
transmitted (Eq 1) and reflected (Eq 3) strain-gage signals does not account for the accumulated damage in the
specimen due to multiple loadings. Therefore, the microstructural changes (or the accumulated strain) in a
specimen cannot be correlated to the macroscopic stress-strain response. For example, in the case of ceramics,
suppose that the amplitude of the incident stress pulse is such that it is slightly below the stress level required
for complete fracture but well above the stress level for initiating microcracking in a ceramic specimen (e.g.,
zirconia ceramics). The repeated loading due to reflected pulses can completely fracture the already weakened
(or microcracked) specimen, but the stress-strain response may indicate otherwise because this is derived from
the first transmitted and reflected pulses only.
The reloading of the specimen due to reflected pulses can be eliminated by using the modified SHPB technique
shown in Fig. 6. In this design, the tensile pulse reflected off the specimen into the incident bar is captured by
the “momentum-trap” assembly designed at the striker end of the incident bar. The technique is described in the
article “Recovery Hopkinson Bar Techniques” in this Volume. Upon impact of the striker, the momentum-trap
design also introduces a tensile pulse following the traditional compression pulse into the incident bar.
Moreover, once a specimen is subjected to the initial compression pulse, all other pulses travelling towards the
specimen end are rendered tensile and, therefore, cannot reload the specimen as the incident bar retracts away
from the specimen. The trapping of the tensile pulse reflected off the specimen has overriding importance in
recovery experiments on some ceramics (e.g., zirconia ceramics), where considerable microcracking and
inelastic deformation can occur before complete fracture of the specimen (Ref 9, 10).

Fig. 6 Schematic of a split-Hopkinson pressure bar test configuration modified with momentum trap.
Source: Ref 11
References cited in this section
2. H. Kolsky, Stress Waves in Solids, Dover, 1963, p 41–94
3. G. Ravichandran and G. Subhash, Critical Appraisal of Limiting Strain Rates for Compression Testing
of Ceramics in a Split-Hopkinson Pressure Bar, J. Am. Ceram. Soc., Vol 77, 1994, p 263–267
4. W. Chen, G. Subhash, and G. Ravichandran, Evaluation of Ceramic Specimen Geometries Used in
Split-Hopkinson Pressure Bar, Dymat, Vol 1, 1994, p 191–210
5. C. Anderson, Jr., P. O'Donoghue, J. Lankford, and J. Walker, Numerical Simulations of SHPB
Experiments for the Dynamic Compressive Strength and Failure of Ceramics, Int. J. Frac., Vol 55,
1992, p 193–208
6. A. Cosculluela, J. Cagnoux, and F. Collombet, Two Types of Experiments for Studying Uniaxial
Dynamic Compression of Alumina, Shock Compression of Condensed Matter, S.C. Schmidt, R.D. Dick,
J.W. Forbes, and D.G. Tasker, Ed., Elsevier Science Publishers, 1991, p 951–954
7. W.R. Blumenthal, High Strain Rate Compression and Fracture of B4C-Aluminum Cermets, Shock-
Wave and High-Strain-Rate Phenomena in Materials, M.A. Meyers, L.E. Murr, and K.P. Staudhmmer,
Ed., Marcel Dekker, 1992, p 1093–1100
8. P.S. Follansbee and C. Frantz, Wave Propagation in the Split-Hopkinson Pressure Bar, J. Eng. Mater.
Technol. (Trans. ASME), Vol 105, 1983, p 61–66
9. G. Subhash and S. Nemat-Nasser, Dynamic Stress-Induced Transformation and Texture Formation in
Uniaxial Compression of Zirconia Ceramics, J. Am. Ceram. Soc., Vol 76, 1993, p 153–165
10. G. Subhash and S. Nemat-Nasser, Uniaxial Stress Behavior of Y-TZP, J. Mater. Sci., Vol 25, 1993, p
5949–5952
11. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery
Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391
Split-Hopkinson Pressure Bar Testing of Ceramics
G. Subhash, Michigan Technological University G. Ravichandran, California Institute of Technology
Limiting (Maximum) Strain Rate
The concept of limiting strain rate for ceramics using a SHPB test originates from the fact that ceramics are
hard and exhibit extremely small strains (<1%) before fracture. Consequently, several of the assumptions
previously discussed are violated. For failure strength data obtained from SHPB experiments to be valid, the
stress in a specimen must be made to reach equilibrium, which means that enough wave reflections must occur
within the specimen before fracture is initiated. This condition imposes limits on either the pulse duration (Eq
6) or the specimen length (Eq 7). The following simple calculations further illustrate this concept (Ref 3). The
time required for an incident wave to travel from one end of the specimen to the other is given by:

(Eq 9)
Let τ be the time required for stress equilibration within the specimen and t
f
be the time to fracture during
loading by the incident pulse. For failure strength data to be valid, t
f
should be greater than or equal to τ.
Assume that the time required for stress to reach equilibrium is an integer multiple of transit time, t
s
, that is:
τ = αt
s
(Eq 10)
where α represents the number of wave reflections within the specimen. The nominal strain rate at the time of
failure in a ceramic that exhibits only elastic strains is given by:
(Eq 11)
where ε
f
is the failure strain. Because t
f
has to be at least equal to τ for failure strength data to be valid,
substituting Eq 9 and 10 in Eq 11 gives the maximum (or limiting) strain rate that can be achieved in a ceramic,
that is:
(Eq 12)
As illustrated in Fig. 2, at least four transit times in a ceramic specimen are required for stress equilibrium to be
achieved (α = 4). Typical ceramic specimen lengths used in SHPB testing are around 9.5 mm (0.375 in.), and
assuming a wave speed of 10,000 m/s (32,800 ft/s) and a failure strain of around 1% in a ceramic, the
maximum strain rate that can be achieved in a ceramic specimen using SHPB testing is around 2600/s. Because
the failure strain and wave velocity are fixed for a given ceramic, acquiring failure strength data beyond this
strain rate requires further reduction in specimen length (and a corresponding reduction in diameter to keep the
length-to-diameter ratio of 2 to 1). For various structural ceramics, this limiting strain rate is found to be in the
range of 2500 to 3000/s (Ref 3).
The concept of limiting (or maximum) strain rate in a ceramic using SHPB testing can also be approached from
the dispersion effects of propagating stress pulses in a slender bar, discussed earlier under the third assumption.
Let us assume that the incident pulse propagating in the bar has a fundamental frequency, ω
o
, and a period, T,
where:
(Eq 13)
Because a typical input pulse in SHPB testing is composed of multiple frequencies, all of which are assumed to
be integer multiples of the fundamental frequency, a characteristic wave velocity is associated with each of the
frequencies, ω, and the corresponding phase velocity, c
p
, is given by:
(Eq 14)
where Λ is the wave length associated with a particular frequency component. The phase velocity can be
obtained from the approximate dispersion relation (Ref 2, 8) given by:
(Eq 15)
where ν is the Poisson's ratio and a is the radius of the bar. For propagating longitudinal stress pulses in a
cylindrical bar, it has been shown that when a/Λ > 0.1, dispersion effects become dominant, and the stress and
displacement fields become highly nonuniform across the cross section of the bar (e.g., Fig. 5b). Therefore, the
data obtained from the surface measurements at distances farther away from the specimen lead to erroneous
results (violation of assumptions 3 and 4). To minimize dispersion, the dominant frequency component in the
frequency spectrum of the incident pulse should be such that a/Λ < 0.1 (Ref 2, 8). This condition can be
rewritten using Eq 13 and 14 as:
(Eq 16)
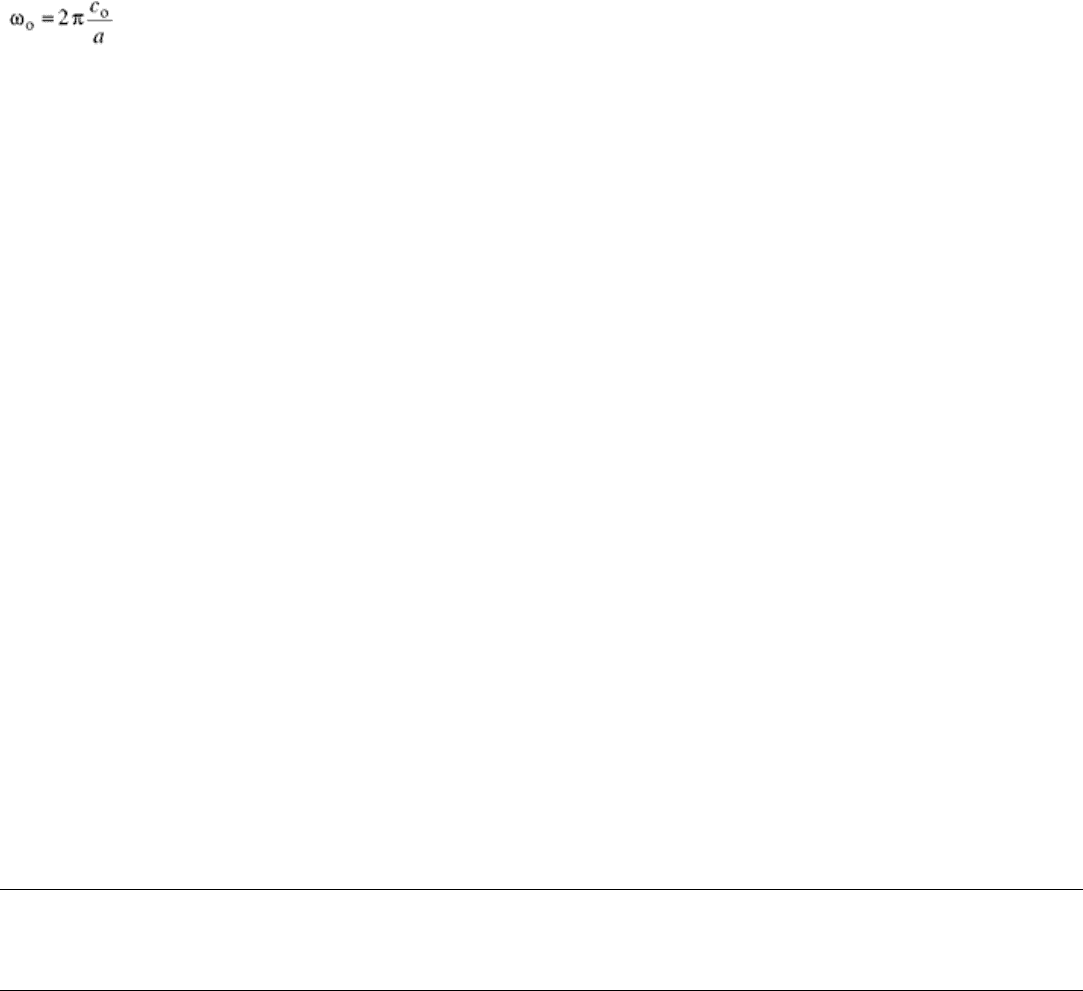
where the fundamental frequency can be determined in terms of bar geometry and material properties as:
(Eq 17)
Using relevant numbers for a 9.5 mm (0.375 in.) diameter SHPB made of maraging steel (a = 4.75 mm, or 0.19
in., ν = 0.3, and c
o
= 4970 m/s), ω
o
can be calculated from Eq 17 as 6.574 × 10
6
rad/s. For a/Λ = 0.1, c
p
can be
calculated from Eq 15 to obtain a limiting value of the fundamental frequency, ω, from Eq 16 as 6.516 × 10
5
rad/s. Finally, the corresponding period, T, of the pulse is calculated from Eq 13 to be 9.64 μs. A given pulse
typically consists of equal durations of loading and unloading phases. Assuming the failure of the specimen
coincides with the peak input load (i.e., at 4.82 μs) for a failure strain of 1% in a ceramic specimen, the
maximum strain rate that can be achieved based on dispersion relation is calculated using Eq 11 to be 2074/s.
This value should be deemed as a lower bound for the limiting strain rate because in 4.8 μs approximately 5
wave reflections can occur for a ceramic specimen of length 9.5 mm (0.375 in.).
From the preceding discussions, it is clear that the maximum strain rate that can be achieved in a ceramic
specimen using SHPB testing can be derived from two approaches: one based on time required for stress to
reach equilibrium in the specimen and the other based on dispersion effects in the propagating pulse. Both
approaches yield the maximum strain rate limit between 2000 and 2600/s. However, this value can be further
extended by reducing the specimen length, decreasing the bar diameter, or increasing the failure strain of the
ceramic material (through microstructural control). However, decreasing the bar diameter will warrant further
reductions in the specimen dimensions so as to obtain the required stress level to cause fracture in a ceramic
specimen.
References cited in this section
2. H. Kolsky, Stress Waves in Solids, Dover, 1963, p 41–94
3. G. Ravichandran and G. Subhash, Critical Appraisal of Limiting Strain Rates for Compression Testing
of Ceramics in a Split-Hopkinson Pressure Bar, J. Am. Ceram. Soc., Vol 77, 1994, p 263–267
8. P.S. Follansbee and C. Frantz, Wave Propagation in the Split-Hopkinson Pressure Bar, J. Eng. Mater.
Technol. (Trans. ASME), Vol 105, 1983, p 61–66
Split-Hopkinson Pressure Bar Testing of Ceramics
G. Subhash, Michigan Technological University G. Ravichandran, California Institute of Technology
Pulse Shaping
Traditionally, a rectangular shaped incident pulse is generated in the incident bar through a planar impact
between the striker and the incident bars. For metallic specimens, this wave form is ideally suited because
metals undergo large plastic strains and the rectangular shaped loading pulse imposes a nominally uniform
strain rate throughout the plastic deformation (Fig. 7a). In the case of a ceramic specimen, use of rectangular
incident pulse is not recommended because ceramics undergo only elastic strain before fracture, and the total
energy contained in the rectangular pulse can be too large to cause excessive fragmentation of ceramics without
any possibility for recovery of the intact but microcracked specimen for post-test quantification and analysis.
Moreover, the rectangular pulse with its steep rise in stress level can impose a nonuniform strain rate during the
elastic deformation of the ceramic due to the differences between the slopes of the imposed loading rate and the
stress-strain response, as shown in Fig. 7(b). Therefore, modification in the incident pulse shape that matches
the slope of the elastic response of the ceramic is recommended. Figure 7(c) illustrates the advantage of using a
ramp pulse while testing ceramics. When incident stress amplitude of the ramp pulse is greater than the stress
required for microcracking in a ceramic, the total energy contained in the ramp pulse beyond the fracture
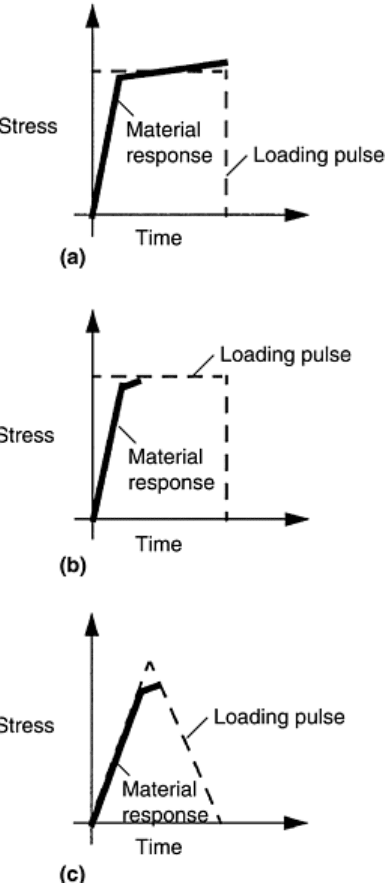
strength is much smaller than the traditional rectangular pulse of similar duration. At the onset of inelasticity
(such as microcracking or transformation plasticity in the case of zirconia ceramics), the remaining duration of
the pulse with excess energy is considerably shorter, and, hence, the cracks have less available time and energy
to propagate, coalesce, and cause catastrophic failure of the ceramic, which can occur if the traditional
rectangular incident pulse of constant duration is imposed. By matching the slopes of the incident ramp pulse
and the stress-strain response, one can also attain a constant strain rate throughout the elastic deformation of the
ceramic.
Fig. 7 Schematic illustration of the influence of incident pulse shaping on the stress-strain response of a
ceramic specimen. (a) Rectangular-shaped pulse on a ductile specimen. (b) Rectangular pulse on a
ceramic specimen. (c) Ramp-shaped pulse on a ceramic specimen
A ramp pulse can be produced by placing a thin ductile (e.g., copper, aluminum) metallic disk of 0.5 to 1 mm
(0.02–0.04 in.) thick and 2 to 3 mm (0.08–0.12 in.) diameter on the impact end of the incident bar, as shown in
Fig. 6. Upon impact by a striker, the plastic deformation of the disk generates a ramp pulse in the incident bar.
The rise and fall times in the ramp pulse can be controlled by changing the material of the pulse shaper as well
as the velocity and length of the striker bar. Figure 8(a) illustrates the traditional rectangular pulse; Fig. 8(b)
shows the typical ramp stress pulse obtained using a copper disk. Note that, although both the pulses are
obtained with the same striker bar, the ramp pulse duration is almost twice that of the rectangular pulse. In-
depth discussions on pulse shaping can be found in Ref 11.
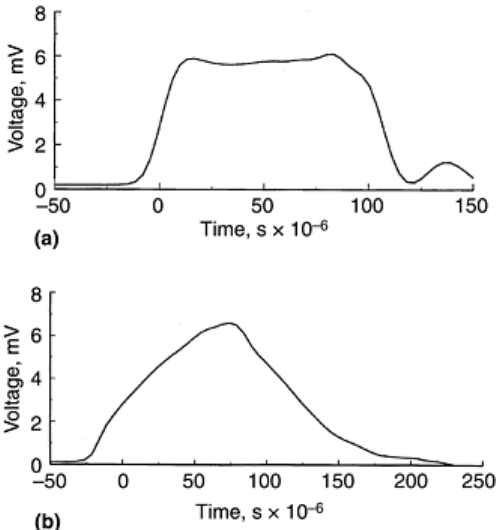
Fig. 8 Comparison of (a) rectangular-shaped pulse with (b) ramp-shaped pulse obtained from the same
length striker bar
Although pulse shaping allows controlled damage in a ceramic specimen at a constant strain rate, use of
traditional SHPB does not preclude the possibility for repeated reloading of the specimen due to wave
reflections in the incident bar. Even if the amplitude of the incident stress pulse is carefully adjusted such that it
is just enough to cause microcracking in the ceramic (but not complete fracture), the reloading of the specimen
by reflected pulses in a traditional SHPB test will suffice to cause complete fracture of the already weakened
(due to microcracking during the first loading) specimen, further emphasizing the need for momentum trapping
discussed previously. With the above modifications, precise stress-strain curves can be obtained in
microcracking ceramics, such as zirconia ceramics, even after significant inelastic strain (due to the stress-
induced transformation) and extensive microcracking have accumulated in the specimen. A typical stress-strain
curve revealing transformation and microcracking phases for magnesia partially stabilized zirconia (MgO-PSZ),
obtained using a ramp loading pulse in a modified SHPB is shown in Fig. 9. In these experiments, strain gages
were mounted on the specimen to obtain the axial and transverse strains during the deformation.
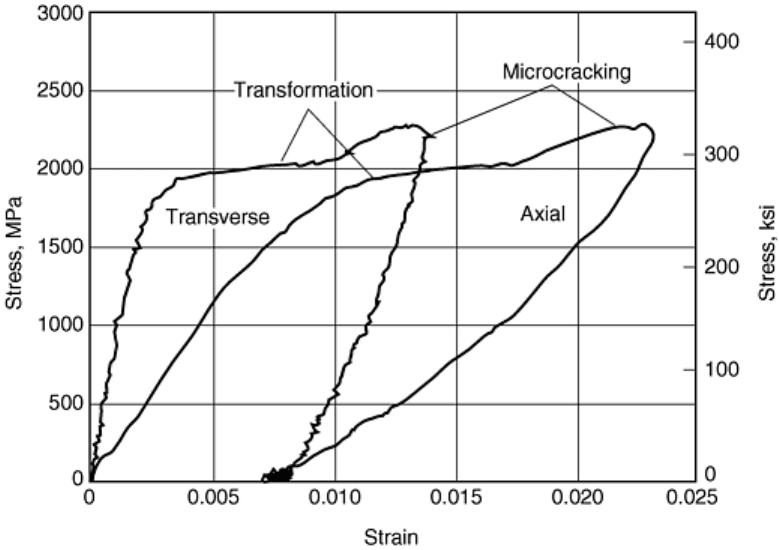
Fig. 9 Stress-strain response obtained using a ramp-shaped pulse in a modified split-Hopkinson pressure
bar test for zirconia ceramic exhibiting inelastic strains associated with stress-induced transformation
and microcracking. Source: Ref 9, 10
References cited in this section
9. G. Subhash and S. Nemat-Nasser, Dynamic Stress-Induced Transformation and Texture Formation in
Uniaxial Compression of Zirconia Ceramics, J. Am. Ceram. Soc., Vol 76, 1993, p 153–165
10. G. Subhash and S. Nemat-Nasser, Uniaxial Stress Behavior of Y-TZP, J. Mater. Sci., Vol 25, 1993, p
5949–5952
11. S. Nemat-Nasser, J.B. Isaacs, and J.E. Starrett, Hopkinson Techniques for Dynamic Recovery
Experiments, Proc. R. Soc. (London) A, Vol 435, 1991, p 371–391
Split-Hopkinson Pressure Bar Testing of Ceramics
G. Subhash, Michigan Technological University G. Ravichandran, California Institute of Technology
Specimen Design
The stress-strain response and failure strength data on ceramics obtained from SHPB is strongly influenced by
the tolerances in the ceramic specimen dimensions, such as parallelism between the end faces, normality of the
end faces with the axis of the specimen, and surface finish. Similar to uniaxial static compression testing of
metals and ceramics, a length-to-diameter ratio of 2 to 1 is recommended for high-strain-rate testing. Because
ceramics have a high elastic modulus (nearly 1.5 to 2 times that of steel) and small failure strains (<1%), small
variations in the parallelism between the end surfaces can cause high stress concentrations at these locations
leading to chipping or initiation of fracture during deformation. Therefore, it is extremely important to grind the
end surfaces to a high degree of flatness (at least 0.01 mm, or 0.0004 in.) and parallelism (within 0.001 mm, or
0.00004 in.) to avoid premature failure of the specimen. Because ceramics are also flaw sensitive, it is
recommended that all surfaces be polished to reduce the influence of machining induced surface flaws.
Interpretation of Test Results
High-strain-rate response of brittle materials, in particular ceramics, differs from quasi-static response in two
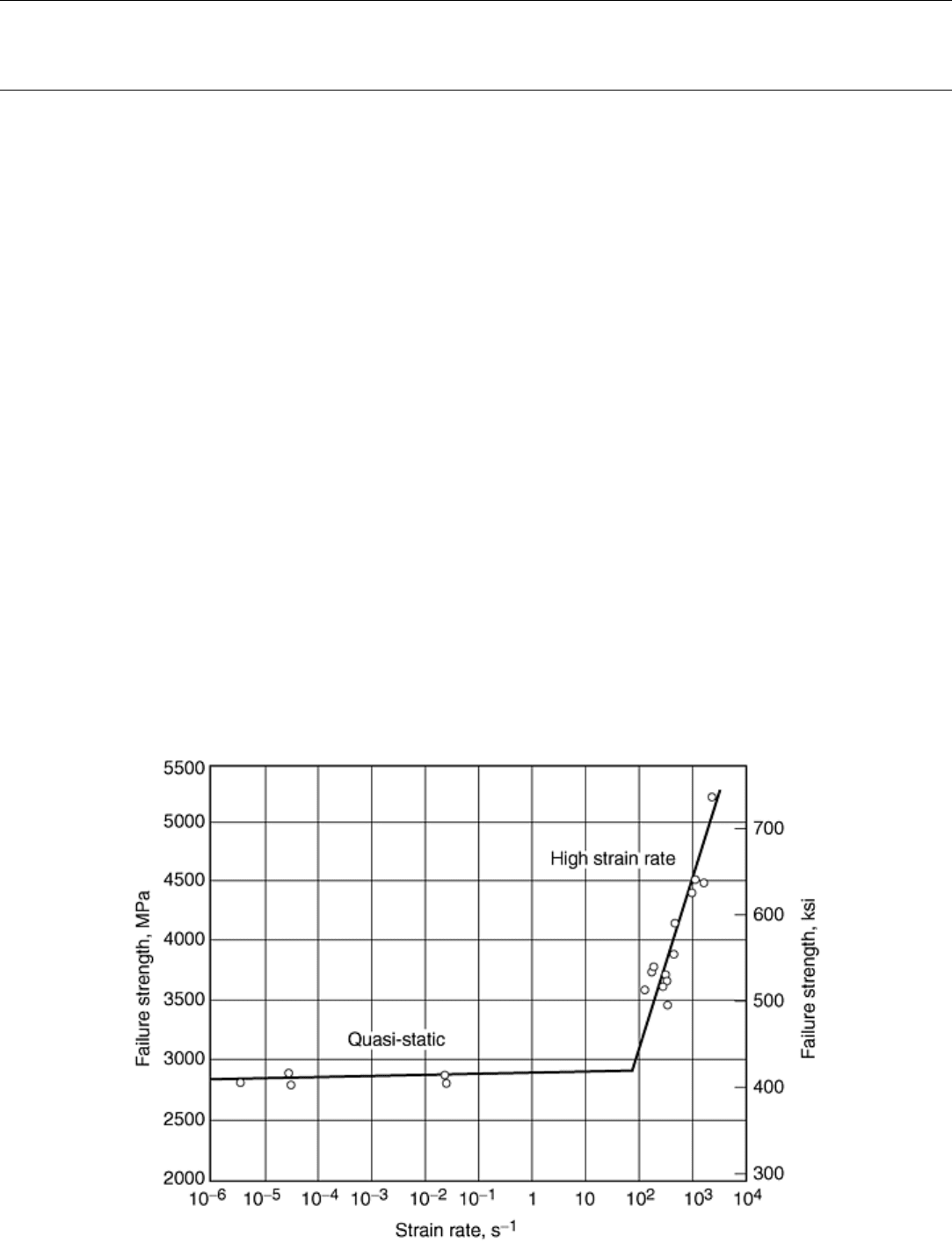
ways. First, there is an increase in fracture strength at high strain rates. Figure 10 illustrates data on aluminum-
nitride uniaxial compressive fracture strength as a function of strain rate. Similar trends were also observed in
several other structural ceramics, such as alumina, silicon carbide, and rocks (Ref 13, 14, 15). Note that, beyond
a critical strain rate, the fracture strength increases with strain rate dramatically. Second, there is an increased
propensity for multiple microcrack initiation from several locations in the specimen. Both these effects are
intimately connected to the inherent microstructure. A brief discussion on the mechanisms of brittle fracture
and damage evolution follows. The discussion is expected to assist a nonspecialist in this field in proper
interpretation of the experimental results obtained using an SHPB test.
Fig. 10 Plot of variation of fracture strength as a function of strain rate for aluminum nitride (AIN)
ceramic. Source: Ref 12
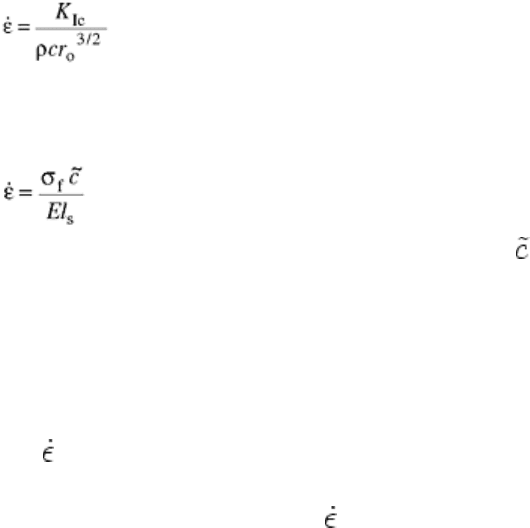
Mechanisms of Brittle Failure Under High-Strain-Rate Loading. It has been well established that processing-
induced microstructural inhomogeneities, such as inclusions, grain boundary impurities, second phases, triple
junctions, and pores are mainly responsible for the nucleation of microcracks that lead to fracture in ceramics
(Ref 14, 16, 17). However, the difference in the characteristics of crack growth from these inhomogeneities is
mainly responsible for the rate-sensitive nature of fracture strength in brittle materials. At low strain rates,
typically below 100/s, both sintered and hot-pressed ceramics, in general, do not exhibit rate-sensitive failure
strength. This behavior has been attributed to unstable crack growth from inhomogeneities and their
instantaneous coalescence, which inhibits any subcritical crack growth.
At high strain rates, beyond a critical strain rate, both sintered and hot-pressed ceramics exhibit a high rate-
sensitive fracture stress due to inertia-dominated crack growth (Ref 14, 15, 17); that is, as the loading rate
increases, the time available for a crack to initiate and grow reduces. The inertia associated with the crack-
growth acceleration will inhibit early fracture initiation while the applied stress continues to rise rapidly, thus
elevating the compressive failure strength under dynamic loads. The critical strain rate at which transition from
the rate-insensitive (unstable) to rate-sensitive (inertia dominated) crack growth in microcracking solids has
been found to depend on material properties. Grady and Lipkin (Ref 18) proposed the following relationship for
the transitional strain rate:
(Eq 18)
where K
Ic
is the fracture toughness, ρ is material density, c is wave velocity, and r
o
is the average initial
microcrack size, which is typically assumed to be the same as the grain size in ceramics. Ravichandran and
Subhash (Ref 17) proposed this equation:
(Eq 19)
where σ
f
is the quasi-static compressive strength and is the characteristic crack velocity which is taken as the
speed at which inertia effects become significant, that is, when the crack velocity reaches approximately 0.2 of
shear wave velocity. Equation 19 is a modified version of the equation proposed by Lankford (Ref 14) where
the length is replaced by radius of the specimen and by shear wave speed. Both Eq 18 and 19 predict the
transitional strain rate to be between 1200 and 1500/s.
In the inertia-dominated (high-strain-rate) regime, the relationship between the compressive fracture strength,
σ
f
, and strain rate at fracture for a variety of brittle ceramics has been found to follow a relationship (Ref 18):
σ
f
α
1/3
(Eq 20)
A micromechanical damage model for brittle materials developed by Ravichandran and Subhash (Ref 17)
shows a similar relationship, σ
f
α
n
, where n ranges from ¼ to ⅓. The value of n depends on the relationship
describing the dynamic fracture toughness as a function of crack speed. Although the relationship discussed
previously has been found to reasonably represent the failure behavior of coarse-grained ceramics, recent
experimental results on fine-grained, high-purity ceramics revealed a complete absence of such a transitional
strain rate (Ref 19, 20). In these ceramics, the uniaxial compressive fracture strength increased linearly with
strain rate in the range between 10
-3
and 10
5
/s. This behavior has been attributed to fine grain size, significant
reduction in the process induced flaws, and elimination of inhomogeneities during processing, all of which
resulted in enhanced dislocation activity and microshear banding similar to those observed in ductile metals.
Damage Evolution. One of the major characteristics of crack growth during uniaxial compressive loading of
brittle materials is that crack growth occurs in a direction parallel to the loading axis. On a plane perpendicular
to the loading axis, the cracks can be randomly oriented, thereby making the specimen transversely isotropic.
The problem of tensile crack growth from preexisting microcracks has been analyzed in detail (Ref 21, 22).
Under uniaxial compressive loading, tensile cracks nucleate from the preexisting flaws in the direction of
maximum tensile stress. The major difference in crack growth under static and dynamic loading is that in static
loading, a single crack typically dominates the fracture behavior. This is because once the stress required for
crack initiation is reached, the weakest crack starts to grow first, and the stored elastic energy continues to
provide the necessary driving force for unstable crack growth to continue and cause eventual failure of the
specimen. Here the rate of loading is extremely slow compared to the crack growth rate, and, hence, once crack
growth is initiated it cannot be controlled. In the case of dynamic loading, the inertia associated with the crack
tip opening delays the crack growth while the applied stress rises much more rapidly beyond that required for
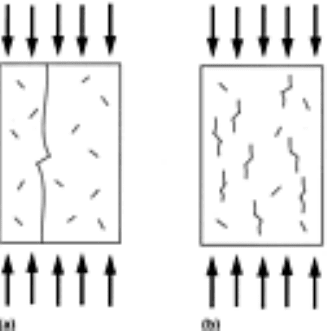
several cracks to grow; therefore, multiple cracks grow simultaneously. The difference in the crack growth
phenomena between static and dynamic loading rates is illustrated schematically in Fig. 11. If the loading
process continues during dynamic testing, the energy required for crack growth continues to be supplied to the
crack tips, leading to complete fragmentation of the specimen. Through proper pulse shaping, the amount of
input energy can be controlled (Fig. 7, 8 ), and microcrack growth can be limited, allowing for recovery of the
intact but microcracked specimen.
Fig. 11 Schematic of crack growth from preexisting flaws under (a) static and (b) dynamic uniaxial
compressive loads
In order to confirm multiple crack growth during dynamic loading, Subhash and Nemat-Nasser (Ref 9)
conducted dynamic uniaxial compression experiments on a MgO-PSZ ceramic specimen in a modified SHPB
with a ramp-shaped input pulse. They subjected the specimen to uniaxial compressive loads successively in two
perpendicular directions. The first loading caused axial crack growth parallel to the first loading direction. The
second loading (in a direction perpendicular to the first one) also induced axial crack growth parallel to this
loading direction. The micrograph provided in Fig. 12 reveals the network of cracks developed parallel to the
two loading directions. Notice that the microcracks developed during the first loading do not seem to influence
the crack growth during the second loading, suggesting that in uniaxial compression, cracks always grow
parallel to the loading axis even in the presence of some material anisotropy caused during the first loading.
Complete recovery of the specimen after multiple microcrack growth was possible due to the controlled energy
input through pulse shaping and ensuring a single loading through modified SHPB testing. With continued
loading, one could expect the specimen to break into columnar fragments due to crack growth from several
locations. Investigations by Kipp and Grady (Ref 23) and Lankford and Blanchard (Ref 16) have confirmed that
fragment size is inversely proportional to the applied strain rate. Smaller fragment size and its narrow
distribution in high-strain-rate experiments imply nucleation and rapid coalescence of numerous microcracks
under dynamic loading, a conclusion that was also supported by the modeling studies on strain-rate effects on
brittle fracture in compression by Nemat-Nasser and Deng (Ref 24).
