ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control

Подождите немного. Документ загружается.

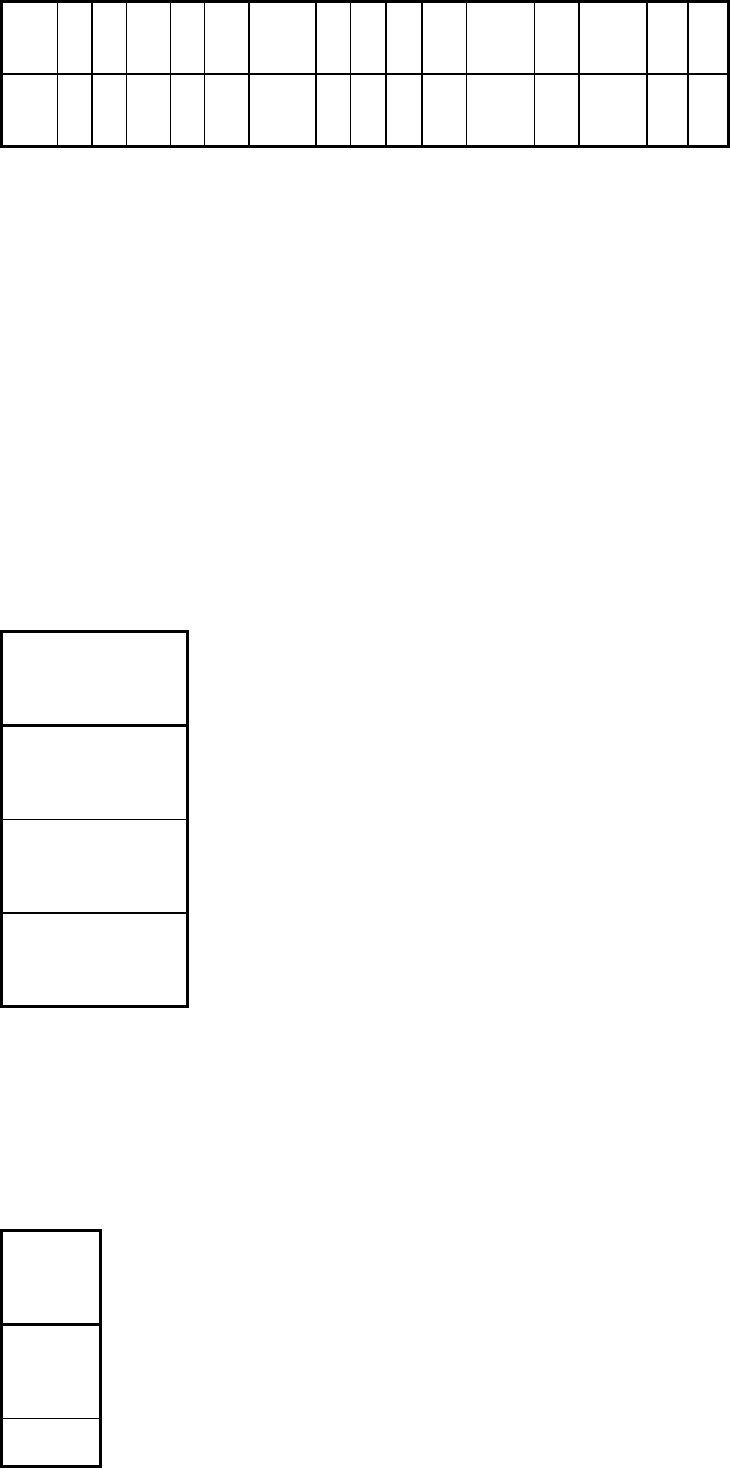
15 2

1 2

1 1 2

1 2 2 1 2 1 1

16 2

1 2

1 1 2

2 1 1 2 1 2 2 1

(a)

e = estimate of error

In this application of the L

) orthogonal array, the following assignments have been made:

• Eight columns have been assigned to variable main effects A, B, C, D, E, F, G, H

• Three columns have been assigned to two-factor interactions A × B, B × D, A × D

• Four columns have been assigned to the estimation of error

Close examination of the L

) orthogonal array shows that the columns assigned to E, G, H, and C are the following

products of the columns assigned to D, B, A, and F:

5 = 234

(E = B × A × F)

7 = 123

(G = C × B × A)

6 = -14

H = -(C × F)

8 = -1234

D = -(C × B × A × F)

It follows then from the associated defining relationship that this L

) orthogonal array is not only a 2

8-4

fractional

factorial but also a Resolution III 2

8-4

design. This is surprising because it is possible to design a 16-run, two-level

fractional factorial to examine eight variables (Resolution IV) using generators such as:

5 = 234

(I = 2345)

6 = 134

(I = 1346)

7 = 123

(I = 1237)

8 = 124

(I = 1248)

The L

) orthogonal array under examination, when viewed as a 2

8-4

fractional factorial design, produces the following

16 linear combinations of effects, which can be estimated from the data. It is assumed that three-factor interactions and

higher can be neglected:

estimates

I (mean)

estimates 1 - 46 - 58

estimates 2

estimates 3

estimates 4 - 16 - 78

estimates 12 + 37

estimates 13 + 27

estimates 6 - 14 - 57

estimates 23 + 45 + 17 + 68

estimates 24 + 35

estimates 34 + 25

estimates 7 - 48 - 56

estimates 26 + 38

estimates 36 + 28

estimates 5 - 18 - 67

estimates

8 - 15 - 47

It is interesting to note the following for this particular 2

8-4

fractional factorial:

• Only two of the eight main effects are not confounded with two-

factor interactions. The other six main

effects are each confounded with two two-factor interactions

• One of the desired two-factor interactions (23) is confounded with three other two-factor interactions

• The four columns assigned to the estimation of error each represent pairs of two-

factor interactions

confounded with each other

An Alternate L

) Orthogonal Approach. It would appear that the L

) orthogonal array using the

generators given below is more suitable for the purposes of Taguchi methods (or any methods for that matter),

particularly given the assumptions generally made about interaction effects:

5 = 234

6 = 134

7 = 123

8 = 124

From this 2

8-4

fractional factorial design, the linear combination of effects (ignoring interactions of three or more factors)

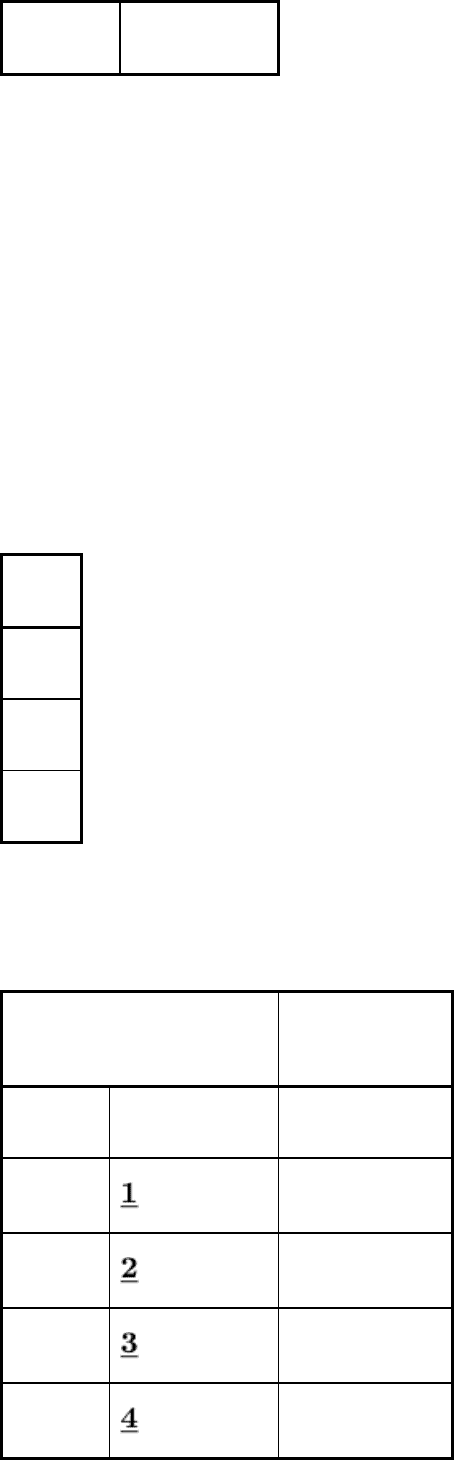
given in Table 17 would result.

Table 17 Linear combination of effects obtained from 2

8-4

fractional factorial design

Effect name in

Taguchi experiment

estimates

I (mean)

(a)

+ 37 + 48 + 56

B × D

+ 46 + 37 + 58

A × D

14 + 36 + 28 + 57

(b)

+ 45 + 17 + 68

A × B

24 + 35 + 18 + 67

(b)

34 + 25 + 16 + 78

(b)

15 + 25 + 47 + 38

(b)

(a)

Underscored effects identify corresponding effects. For example, is D, is B, and so on, in

Taguchi's experiment.

(b)

e = estimate of error

The following conclusions can be drawn from Table 17:

• All eight main effects are confounded with three-factor and higher--only two previously

• All three desired two-factor interactions are confounded with three other two-factor interactions--

only

one previously

• All four error estimates are a set of four confounded two-

factor interactions; previously, they were sets

of two confounded two-factor interactions. This is a trade-

off for the estimation of two of the desired

two-factor interactions: B × D and A × D

Choice of Variables in Calculation Matrix. When fewer than k = n - 1 variables are studied in 2

k-p

= n tests, some

choice exists in terms of how variables (main effects) are assigned to columns in the L

) array (the calculation matrix).

Some choices are often better than others in terms of the resulting design resolution. Under the Taguchi approach to

design of experiments, the philosophy toward interaction effects is quite different. As a result, the bottom line is that

unless they are expressly identified and assigned to the orthogonal array, they are assumed to be neglectable. If such an

attitude is adhered to, it is perhaps of even greater importance to place emphasis on design resolution and the careful

examination of the alias structure of the experimental design. When higher-resolution designs (arrays) are available, it is

of utmost importance to seek them out in an effort to protect the assumptions used. Again, Example 11 demonstrates the

importance of design resolution and the judicious choice of design generators. In the context of Taguchi's approach to

design of experiments, this is even more important because the sequential assembly concept is not used; that is, single

experiments tend to be employed on any given problem.

References cited in this section

4. G. Taguchi and Y. Wu, Introduction to Off-Line Quality Control,

Central Japan Quality Control

Association, 1979

7. G.E.P. Box and J.S. Hunter, The 2k-p Fractional Factorial Designs, Part I and Part II, Technometrics,

Vol 3,

1961

8. G.E.P. Box, W.G. Hunter, and J.S. Hunter, Statistics for Experimenters, John Wiley & Sons, 1978

26.

D.J. Finney, The Fractional Replication of Factorial Arrangements, Ann. Eugen., Vol 12, 1945, p 291-301

27.

C.R. Rao, Factorial Experiments Derivable From Combinatorial Arrangements of Arrays,

J. Royal Stat.

Soc., Vol B9, 1947, p 128-140

28.

L.H.C. Tippett, Applications of Statistical Methods to the Control of Quality in Industrial Production,

Manchester Statistical Society, 1934

29.

R.L. Plackett and J.P. Burman, Design of Optimal Multifactorial Experiments, Biometrika,

Vol 23, 1946, p

305-325

Statistical Quality Design and Control

Richard E. DeVor, University of Illinois, Urbana-Champaign; Tsong-how Chang, University of Wisconsin, Milwaukee

Implementing Robust Design

Recently, a number of different approaches have been proposed as possible ways to implement the robust design concept

of Taguchi. These vary from purely analytical approaches, to computer simulation using product/process mathematical

models and/or Monte Carlo methods, to the use of physical experimentation. In most of these approaches, the use of

experimental design strategies, including two-level and multilevel factorial and fractional factorial designs and orthogonal

arrays, has been extensive.

Taguchi views the design process as evolving in three distinct phases or steps:

• System design

• Parameter design

• Tolerance design

It is perhaps this broad umbrella that he places over his concepts and methods for quality design and improvement that

makes his approach so widely accepted by the engineering community. As discussed previously, Taguchi considers

engineering design as the central issue and statistical methods as just one of several tools to accomplish his objectives in

engineering.

In addition to the different approaches to generating data on product/process performance, the issue of the specific

measures of performance to use in the facilitation of parameter design needs to be considered. Taguchi and his colleagues

make extensive use of the signal-to-noise ratio as a measure of performance. Others evaluate the mean and the variance or

standard deviation of performance separately. The relative merits of these varying approaches with regard to performance

evaluation will be discussed later in this article. The separate analysis of mean response and variation in response is

discussed below.

Degree of Control

The issue of the control of a certain factor is actually one of economics; therefore, any factor might be thought of in terms

of its degree of control rather than as controllable or not controllable. Suppose that an injection-molding process is under

consideration because of a part shrinkage problem. A brainstorming session might lead to the following list of factors as

potentially having an influence on part shrinkage:

• Cycle time

• Percentage of regrind versus virgin raw material

• Gate configuration

• Holding pressure

• Screw speed

• Mold temperature

• Cavity surface finish

• Raw material moisture content

• Raw material melt flow index

• Mold cooling water temperature

Although any or all of these factors can influence part shrinkage, they are not all controlled or manipulated to the same

degree or with the same ease, economically. Some of these factors can be controlled at the engineering design process--

for example, the gate configuration or the cavity surface finish of the mold. Others are controllable at the molding

machine--for example, screw speed or cycle time. Still others are properties of the incoming raw material and are thus

under the control of the supplier--for example, melt flow index. Finally, certain factors can be best categorized as defining

part of the environment in which the process must function--for example, mold cooling water temperature and percentage

of regrind versus virgin raw material. Two case studies will be discussed that exemplify some of the different ways in

which the concept of parameter design can be implemented to develop robust product and process designs.

Analytical Approaches to Parameter Design

It is important to keep a broad perspective on the contributions of Taguchi and the wide variety of ways in which they can

be utilized. Perhaps the single overarching concept that drives the philosophies of Taguchi is the importance placed on the

consistency of performance of products and processes, that is, the importance of variation reduction. In essence, as

designs are formulated and output performances evaluated, either analytically or experimentally, as much or more

emphasis should be placed on variation in performance as on performance on average. There are many ways to invoke

this overarching concept.

Although much of the knowledge used in a given design situation is derived from experimentation, an ever-expanding

baseline of knowledge exists that is being derived from first principles/physical laws and the utilization of sophisticated

modeling methods such as finite-element modeling. As closed form solutions become available, it becomes possible to

evaluate them analytically or numerically using classical optimization methods. The performance function should be

examined in terms of both its expected value and its variance function. Searching the variance function to find those

values for the design/control variables that minimize the variance in performance then amounts to invoking the parameter

design method.

Example 12: Parameter Design Methods Applied to Analysis of Effort Required to Close

an Automobile Door

(Ref 30). An explicit model is used for the mean square error of design performance in an automobile door-closing-effort

problem to identify the values of the design parameters that provide the most consistent design configuration (minimum

variance) while maintaining an acceptable level of average performance. In this case study, the following

logic/methodology is employed.

Problem Formulation. The first step in any design optimization problem is to formulate the design performance

measure of interest. In this case study, automobile door fit is the issue, particularly the sensitivity of the closing effort to

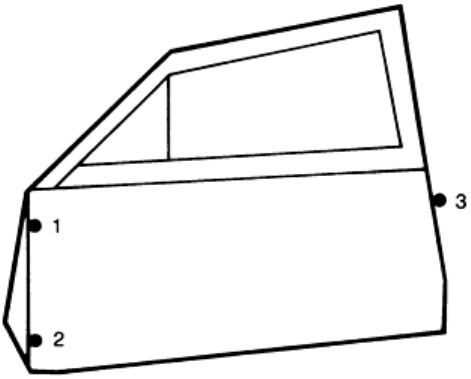
variations in door positioning as it is hung in place. Figure 44 illustrates a car door and the locations of the three

positioning points used to hang the door. The closing effort is a function of the compression of the weatherstripping

around the door periphery. The closing effort can be expressed analytically as a function of the weatherstripping diametral

stiffness, the weatherstripping diameter and length, and the nominal values of the door position points that define the

door/frame gap. The basic design problem is then to find the nominal values for the door position points that minimize the

variation in closing effort as a result of the tolerance range assigned to the door position points. This problem was

formulated in an attempt to exploit the underlying nonlinearities in the system to improve performance consistency.

Fig. 44 Schematic of an automobile door showing loca

tions (solid circles) of three positioning points used to

hang the door

Model Derivation. Under the assumption that the door gap is linearly proportional to the door position point locations,

it is possible to derive the door-closing effort (in stored energy) as a quadratic function of the position point locations. The

position location points are the control factors in this problem. The quadratic function for closing effort as a function of

the three hanging positions has several unknown parameter values. Although the closing effort will clearly vary as a

function of variation from car to car in the weatherstripping thickness, car body, size, and so on, only the variation in the

door hanging position from car to car was examined in this case study.

Model Fitting. The parameters of the quadratic function for closing effort were estimated by first calculating the door

gap at 15 points around the door as a function of variations in the door hanging positions and then using the calculated

gap values to determine the closing-effort values. The variations in the hanging position control factors were introduced

using a three-level factorial design, which required a total of 27 evaluations of the gap and the stored energy at each of the

15 locations around the door. These data were then used to estimate the coefficients of the quadratic closing-effort

function.

Design Optimization. The variance of the closing-effort quadratic function can now be derived analytically, and this

variance function can be subjected to a classical optimization routine. Such an optimization algorithm will seek the values

of the three door position locations that minimize the variance of the closing effort. This optimization is subject to the

constraint that the mean closing effort is less than or equal to a prespecified target value. The result is the determination of

the nominal values for the design/control factors, that is, the door positioning locations that minimize the car-to-car

closing-effort variation because of variation in these locations. In this design optimization problem, the control factors are

the nominal values for the door position locations, and the noise factors are the tolerance/variations in the door position

locations.

Figure 45 shows a plot of the derived functional relationship between closing effort and the location of point 1 for

positioning the door for fixed values of location points 2 and 3. Figure 45 clearly shows how the parameter design method

exploits a basic system nonlinearity by seeking a new nominal value for the location of point 1 that reduces the

transmitted variation to the closing effort due to the variation in the location of point 1 about its nominal value.

Fig. 45 Plot of closing effort versus point 1 location for positioning the door shown in Fig. 44

with fixed values

of location points 2 and 3

Experimental Approaches to Parameter Design

The parameter design concept can be implemented through physical experimentation in many different ways. The

following example illustrates the explicit use of an inner/outer design for robust design. The example was developed from

the results of a larger experiment and is presented to demonstrate how simple experiments such as two-level factorial

designs can be used to study and improve the performance of an assembly process using the concept of robust design.

Example 13: Optimization of Automotive Fuel Gage Reading to Actual Fuel Tank

Quantity.

Customer complaints regarding the difference between the fuel gage reading and the actual amount of fuel in the tank led

to an investigation of the process of gage calibration. Seven variables were tentatively identified as being of possible

importance to the position (% deflection or fallback) of the indicator in the fuel gage.

Initial Design of Experiments. A 2

7-3

fractional factorial design experiment was constructed and carried out. A

portion of the results will be examined that involve four of the seven variables determined to be the most important. These

four variables are:

Variable No.

Variable Low level

High level

1 Spring tension Loose

Tight

2 Method of pointer location

Visual

Other (standard)

3 Bimetal hook twist Vendor A

Vendor B

4 Bimetal bracket bend 90° 93°

Variables 1 and 2 describe adjustments that can be made during the calibration process on the assembly line. Variables 3

and 4 describe the condition (considered undesirable) of certain purchased parts that are assembled into the gage and may

affect the calibration process. The 2

7-3

fractional factorial design was collapsed into a 2

full factorial design to study the

effects of these variables, as they are purposely changed, on the response in question.

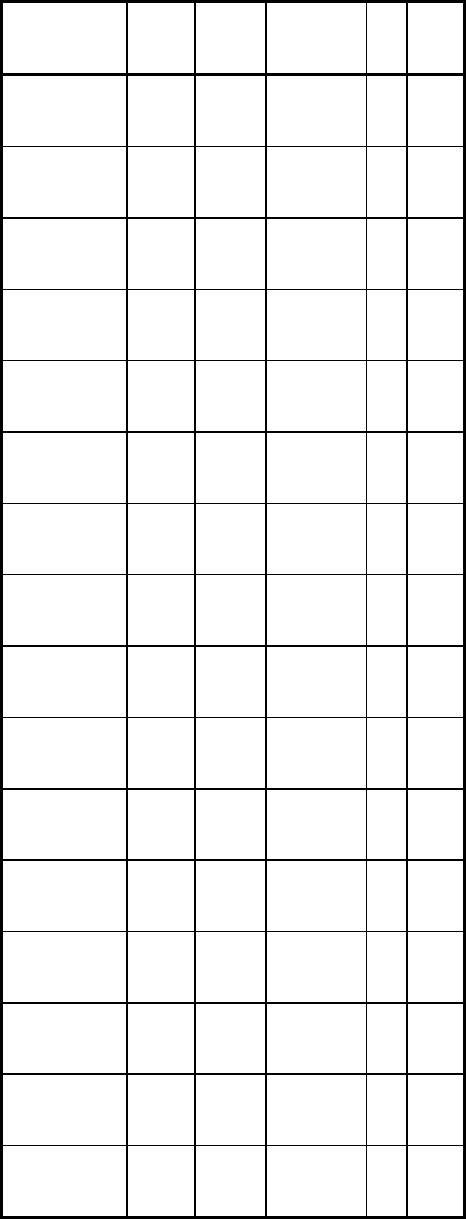
Table 18, the design matrix, lists the settings for the 16 tests conducted in terms of the four variables defined above. The

tests are listed in standard order, although they were actually run in a randomized test sequence.

Table 18 Design matrix for fuel gage experiment of Example 13

Test number

Y, %

1 Loose

Visual

Vendor A

2 Tight Visual

Vendor A

3 Loose

Other Vendor A

4 Tight Other Vendor A

5 Loose

Visual

Vendor B 90

6 Tight Visual

Vendor B 90

7 Loose

Other Vendor B 90

8 Tight Other Vendor B 90

9 Loose

Visual

Vendor A

10 Tight Visual

Vendor A

11 Loose

Other Vendor A

12 Tight Other Vendor A

13 Loose

Visual

Vendor B 93

14 Tight Visual

Vendor B 93

15 Tight Other Vendor B 93

16 Tight

Other

Vendor B

The main effects of each of the four factors, as well as the two-, three-, and four-factor interactions, were estimated from

the data and are listed below:

= -2.50

= 0.00

= -1.75

= 3.00

= 0.50

= 1.75

= -1.00

= 2.25

= 0.50

= -1.25

123

= 0.75

124

= -2.50

134

= 0.75

234

= 0.25

1234

= -2.25

The results of the larger experiment, in fact, showed that these four variables tended to exhibit the stronger effect

estimates, both main effects and interactions. A normal probability plot of the estimated effects could be interpreted as

suggesting that only the effect estimates indicated by the asterisk might be considered insignificant. This interpretation

leaves the investigator somewhat perplexed as to what exactly to do next. Many interactions seem important, yet it is not

at all clear how the process can best be adjusted/altered.

It would appear that the main effects of variables 1 and 4 might be two of the more important effects:

• E

= -2.50, implies that, on the average, tighter spring tension reduces fallback (deflection)

• E

= +3.00, implies that larger bimetal bracket bends (93°) increase deflection, which is undesirable

The latter inference suggests that closer adherence to the 90° bend, which is the desired nominal value, may have to be

requested from the bimetal bracket supplier. This essentially means that the supplier would be required to tighten the

tolerance on this angle. Rather than taking this more costly approach, it might be useful to consider the variation in this

part dimension as a noise variable and then determine how the transmission of the variation in the bimetal bracket bend

could be reduced through the manipulation of control factors during the calibration process.

Alternative Experimental Design and Analysis. A more thoughtful examination of the four variables under study

seems to indicate that they fall into two basic categories. The first category consists of:

• Variable 1: Spring tension

• Variable 2: Method of pointer location

The second category consists of:

• Variable 3: Bimetal hook twist

• Variable 4: Bimetal bracket bend

Variables 1 and 2 can be easily adjusted at the discretion of the operator/setup person. Variables 3 and 4 describe certain

aspects of the condition of two purchased parts. Although the vendors have been given certain requirements, strong

control is not exercised over these factors (which determine the condition of the parts coming in) without tightening the