ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control

Подождите немного. Документ загружается.

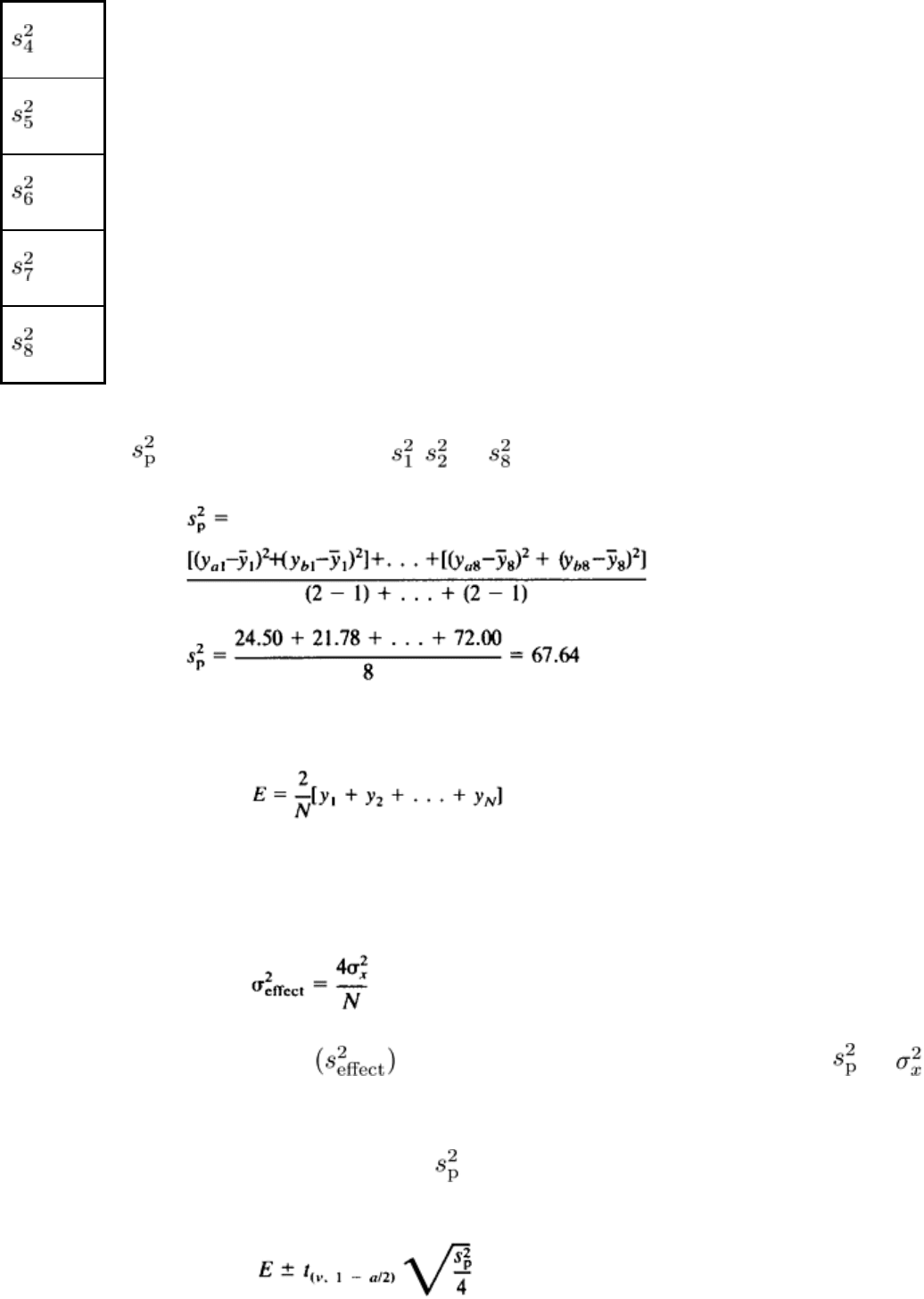
= 242.00

= 3.92

= 8.82

= 33.62

= 72.00

Because there is assumed to be a common variance for all 16 observations, an estimate for the variance is the pooled

sample variance , of the 8 estimated variances , , . . . . In this case:

(Eq 16)

In general, an effect is determined from:

(Eq 17)

where N is the total number of unique test/trial results.

In this general case, the variance of an effect is given by:

(Eq 18)

An estimate of the variance of an effect is obtained by substituting the pooled sample variance, , for .

A confidence interval for a certain parameter can be calculated on the basis of the sample statistic. Here the statistics of

interest are the average effects, E

, E

, and the interactions, E

, E

, and E

123

. Because the sample variances of the

average effects and interactions are all estimated by /4, the result, for 100(1 - a)% confidence intervals using the

Student's t-statistic, is:

(Eq 19)

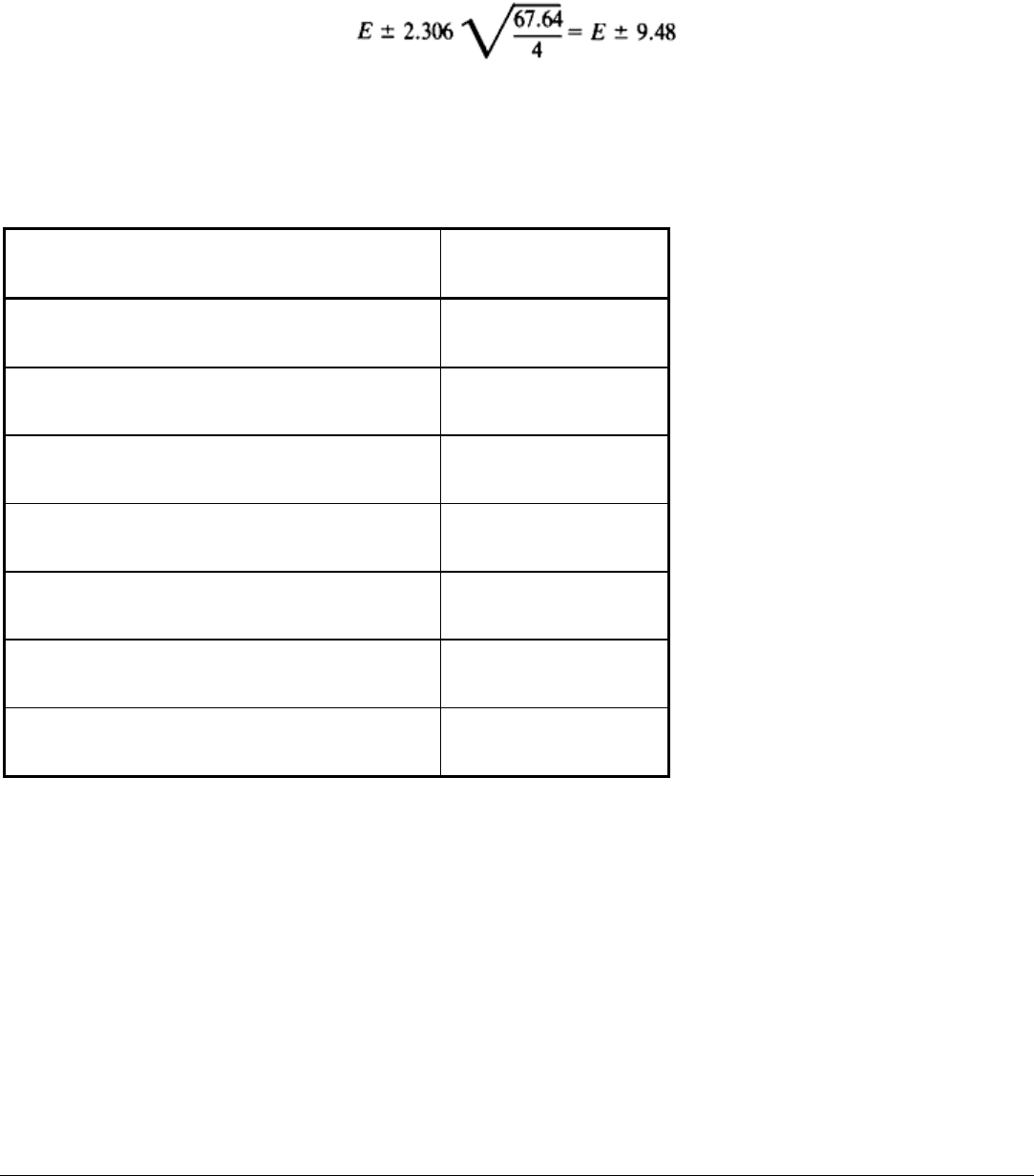
where v = 8 is the degree of freedom and a = 0.05 is the level of significance. Therefore, the 95% confidence intervals for

each of the sample average effects are therefore:

Table 13 gives the seven statistics (E

, E

, and E

123

) together with their corresponding 95% confidence

intervals. From Table 13, it would appear that none of the estimated effects is important/significant.

Table 13 Calculation of 95% confidence levels for average effect and interaction statistics of steel rail b

ars

of Example 8

Average effects

95% confidence interval, psi

Ambient temperature (E

)

9150 ± 9480

Wind velocity (E

)

-5100 ± 9480

Bar size (E

)

850 ± 9480

Ambient temperature × wind velocity (E

)

0 ± 9480

Ambient temperature × bar size (E

)

-4650 ± 9480

Wind velocity × bar size (E

)

-100 ± 9480

Ambient temperature × wind velocity × bar size (E

123

)

4700 ± 9480

Unreplicated Factorial Designs. There are times when it is either not feasible or not desirable to include replication

in a two-level factorial design. In such cases, it is therefore not possible to obtain a direct estimate of the experimental

error; as a result, it becomes more difficult to assess the relative importance of the variable effects. There are, however, at

least two methods that can be employed to aid in the assessment of the relative importance of variable effects estimated

from the results of an unreplicated two-level factorial design. These two methods are:

• The use of normal probability plots of the effect estimates

• The use of higher-

order interaction effect estimates as a means to obtain an estimate of the experimental

error

These methods are discussed in Ref 7 and 25.

References cited in this section

7. G.E.P. Box and J.S. Hunter, The 2k-p Fractional Factorial Designs, Part I and Part II, Technometrics,

Vol 3,

1961

8. G.E.P. Box, W.G. Hunter, and J.S. Hunter, Statistics for Experimenters, John Wiley & Sons, 1978

23.

S.M. Wu, Analysis of Rail Steel Bar Welds By Two-Level Factorial Design, Weld. J. Research Supplement,

April 1964

24.

R.E. DeVor and T.H. Chang, Quality and Productivity Design and Improvement: Module 2, in

Statistical

Process Control, Ford Motor Company, Plastic Products Division, 1988

25.

R.E. DeVor and T.H. Chang, Statistical Methods for Quality and Productivity Design and Improvement, in

The Tool and Manufacturing Engineer's Handbook, Vol 4, Society of Manufacturing Engineers, 1987

Statistical Quality Design and Control

Richard E. DeVor, University of Illinois, Urbana-Champaign; Tsong-how Chang, University of Wisconsin, Milwaukee

Two-Level Fractional Factorial Designs

Although the class of two-level factorial designs appears to be an efficient way to deal simultaneously with several

factors, this efficiency quickly disappears as the number of variables to be studied grows. Because the two-level factorial

requires the consideration of all possible combinations of k variables at two levels each, a ten-variable experiment would

require 2

= 1024 tests.

In dealing with phenomena involving continuous variables, the relationship that describes the influence of the variables

on a response of interest often constitutes a relatively smooth response surface. When dealing with qualitative (discrete)

variables, it is usually the case that the responses are similar at different levels of such variables. Therefore, the higher-

order variable interactions are often very small or negligible in magnitude. In fact, interaction effects involving three

factors or more can be ignored for the purpose of screening out the much more important main effects and two-factor

interaction effects from a limited number of tests.

Experimentation with large numbers of variables generally arises out of uncertainty as to which variables have the

dominant influence on the response of interest. In the end, however, only a subset of all these variables will be proved to

be important. This phenomenon is referred to as the sparsity of variable effects (Ref 8). If this is the case, one should be

able to conduct fewer tests than required for the full factorial without much loss of relevant information.

Consequences of Fractionation

In the rail steel bar problem, three variables (ambient temperature, wind velocity, and bar size) were studied to determine

their possible effect on the ultimate tensile strength of the welded bars. A 2

full factorial design was run, and the three

main effects, three two-factor interaction effects and the one three-factor interaction effect could all be estimated

separately. Suppose now that the investigator had wished to consider a fourth variable, type of welding flux, but that the

full factorial, 2

= 16 tests, could not be considered. Rather, only 8 tests can be run. Is it possible to conduct an

experiment on 4 factors with only 8 tests, and if so, what useful information can be obtained from the results?

Based on the assumption about the negligible third and higher-order interaction effects, one could consider assigning the

column of plus and minus signs associated with the 123 interaction to be the fourth variable and estimate the average

main effect of variable 4 using this column. In using the 123 column to introduce a fourth variable into the experiment,

the new design matrix that defines the 8 tests to be conducted becomes:

Variables

Test

4 (123)

(a)

1 - - -

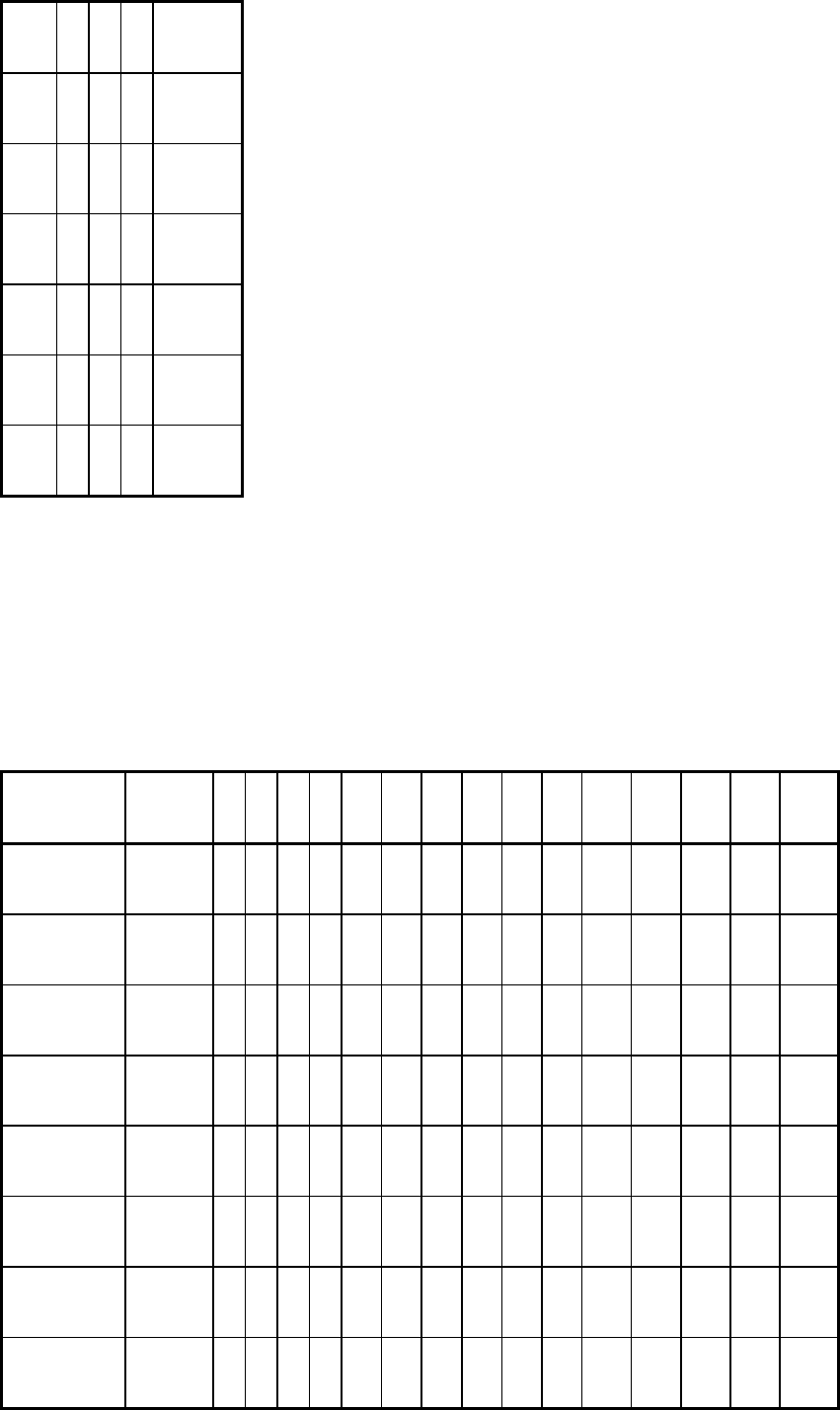
2 +

- -

3 - +

4 +

5 - - +

6 +

- +

7 - +

8 +

(a)

123 column replaced by

variable 4

Once the tests are conducted in accordance with the test recipes defined by the design matrix, the calculation matrix is

determined to provide for the estimation of the interaction effects. By expanding the design matrix above, Table 14

provides the calculation matrix obtained by forming all possible products of columns 1 through 4.

Table 14 Calculation matrix obtained by expanding the design matrix

Test number

Average

123

124

134

234

1234

1 + - - - - + + + + + + - - - -

2 + +

- - +

- - + + - - + - - +

3 + - +

- +

- + - - + - + - + -

4 + +

- - + - - - - + - - + +

5 + - - +

+ - - - - + + + - -

6 + +

- +

- - + - - + - - + - +

7 + - +

- - - + + - - - + + -

8 + +

+ + + + + + + + + + +

Examination of the calculation matrix in Table 14 reveals that many of the columns are identical. In particular, of the 16

columns, only 8 are unique; each unique column appears twice. The following pairs of variable effects are represented in

the calculation matrix by the same column of plus and minus signs:

1 and 234

2 and 134

3 and 124

4 and 123

12 and 34

13 and 24

23 and 14

Ave and 1234

What does all this mean? For example, when the 12 column is multiplied by the data, summed, and divided by 4, is the

result an estimate of the two-factor interaction 12? Or the two-factor interaction 34? Or both? The interactions 12 and 34

are said to be confounded or confused. They are aliases of the unique column of plus and minus signs defined by (+ - - +

+ - - +). Use of this column for effect estimation produces a number (estimate) that is actually the combined total of the

two-factor interaction effects 12 and 34. Similarly, 1 and 234 are confounded effects, 2 and 134 are confounded effects,

and so on. It seems that the innocent act of using the 123 column to introduce a fourth variable into a 2

full factorial

scheme has created a lot of confounding among the variable effects, but if all the three-factor interactions are negligible,

one obtains clear estimates of all 4 main effects from only 8 tests.

The 2

k-p

Fractional Factorial Designs. The four-variable, eight-test, two-level experiment discussed thus far is

referred to as a two-level fractional factorial design because it considers only a fraction of the tests defined by the full

factorial. In this case, a one-half fraction design has been created. It is commonly referred to as a 2

4-1

fractional factorial

design. It is a member of the general class of 2

k-p

fractional factorial designs. In these designs, the following factors must

be considered:

• k variables are examined in 2

k-p

tests

• Require that p of the variables be introduced into the full factorial in k-p variables

• Assign them to interaction effects in the first k-p variabl

es. This assignment is done through the use of

relationships known as generators (Ref 7, 8)

• These generators can then be used to establish the defining relationship (Ref 7, 8

), which completely

reveals the confounding/alias structure of the experimental design

Resolution of Two-Level Fractional Factorial Designs. As discussed previously, the introduction of additional

variables into full two-level factorials gives rise to confounding or aliasing of variable effects. It would be desirable to

make this introduction in such a way as to confound low-order effects (main effects and two-factor interactions)--not with

each other but with higher-order interactions. Then, under the assumption that third and higher-order interactions can be

neglected, the low-order effects become, in a sense, unconfounded by this assumption.

To illustrate, consider the study of 5 variables in just 16 tests (the full factorial would require 2

= 32 tests). One

additional variable--the fifth variable--must be introduced into a 2

= 16 run base design. Any of the interactions in the

first 4 variables could be used for this purpose: 12, 13, 14, 23, 24, 34, 123, 124, 134, 234, 1234. If any one of the two-

factor interactions are used, for example, 5 = 12, then the design generator becomes I = 125, which is also the defining

relationship. Therefore, at least some of the main effects will be confounded with two-factor interactions, namely, 1 = 25,

2 = 15, 5 = 12.

Selecting Preferred Generators. If any one of the three-factor interactions is used to introduce the fifth variable, the

situation is greatly improved, at least for the estimation of main effects. For example, if 5 =123, then I = 1235 is the

generator and defining relationship; therefore, some main effects are confounded with, at worst, three-factor interactions,

while two-factor interactions are confounded with each other, for example:

1 = 235

2 = 135

3 = 125

5 = 123

12 = 35

13 = 25

23 = 15

If the four-factor interaction in the first 4 variables is used to introduce the fifth variable, an even more desirable result is

obtained (the best under these circumstances): 5 = 1234. The generator and defining relationship is I = 12345. Therefore:

1 = 2345

2 = 1345

3 = 1245

4 = 1235

5 = 1234

12 = 345

13 = 245

14 = 235

15 = 234

23 = 145

24 = 135

25 = 134

34 = 125

35 = 124

45 = 123

In this last case, all main effects are confounded with four-factor interactions, and all two-factor interactions are

confounded with three-factor interactions.

Concept of Resolution. The varying confounding structures produced by using different orders of variable

interactions to introduce the fifth variable in the example above are described by the concept of the resolution of

fractional factorial designs. The resolution of a two-level fractional factorial design is defined to be equal to the number

of letters (numbers) in the shortest-length word (term) in the defining relationship, excluding I. If the defining relationship

of a certain design is I = 124 = 135 = 2345, then the design is of Resolution III. If the defining relation of a certain design

is I = 1235 = 2346 = 1456, then the design is of Resolution IV. The last design examined above, which had the defining

relationship I = 12345, is a Resolution V design. These concepts can be summarized as follows:

• If a design is of Resolution III, this means that at least some main effects are confounded with two-

factor interactions

• If a design is of Resolution IV, this means that at least some main effects are confounded with three-

factor interactions, while at least some two-factor interactions are confounded with other two-

factor

interactions

• If a design is of Resolution V, this means that at least some main effects are confounded with four-

factor interactions, and some two-factor interactions are confounded with three-factor interactions

Example 9: Design Resolution/Selection of Generators.

A 2

6-2

fractional factorial design is set up by introducing variables 5 and 6 via 5 = 123, 6 = 1234. What is the resolution of

this design?

The design generators are I = 1235 = 12346, with the defining relationship I = 1235 = 12346 = 456. Therefore, the design

is of Resolution III.

What would the resolution be if the generators were 5 = 123 and 6 = 124? Because the defining relationship is I = 1235 =

1246 = 3456, the design is of Resolution IV. It is clear that the selection of the proper design generators is very important.

Additional Observations on Design Resolutions. From the above discussion on design resolution, several

observations can be made:

• Higher-resolution designs seem more desirable because they provide the opportunity for low-

order

effect estimates to be determined in an unconfounded state, assuming higher-order interaction effe

cts

can be neglected

•

The more variables considered in a fixed number of tests, the lower the resolution of the design becomes

•

There is a limit to the number of variables that can be considered in a fixed number of tests while

maintaining a prespecified resolution requirement

• No more than (n - 1) variables can be examined in n tests (n

is a power of 2, for example, 4, 8, 16, 32, . .

.) to maintain a design resolution of at least III. Such designs are commonly referred to as saturated

designs. Examples are 2

3-1

, 2

7-4

, 2

15-11

, 2

31-26

. For saturated designs, all interactions in the base design

variables are used to introduce additional variables

Importance of Sequential Experimentation

In the early stages of an investigation, it often seems that many variables are of potential importance. A project group or

task force can draw up a list of 5 to 15 or more variables. In the final analysis, perhaps only 2 or 3 of these variables will

prove to be important. The problem is, Which ones? The first task at hand is to conduct some experiments that will

quickly reduce the number of variables under study to the few seemingly important ones that will then be the focus of

further experimentation. For this screening task, two-level fractional factorial designs constitute a powerful and efficient

tool. If the investigator attempts to get his arms around the entire problem by designing one comprehensive experiment,

the resource requirements will probably be extensive, and the final results of the experiment may be inconclusive because

of poor selection of variable levels and/or a poorly controlled experimental environment precipitated by a large

experiment.

It would be wise to take a sequential approach, building up knowledge more gradually through a series of related

experiments. In this regard, two-level fractional factorial designs serve as useful building blocks in a course of sequential

experimentation. This notion is important to ensure that a lack of knowledge early in an investigation will not lead to the

waste of experiment resources--for example, inappropriate variables or variable levels chosen in the context of one large

experiment. It is possible to identify families of experiments that combine or piece together well. A key point here is that

these related experiments can provide several different alternatives for a second experiment, depending on the results and

inferences drawn from the first experiment. The sequential assembly aspect of related experiments is discussed below.

Example 10: Notion of Families of Fractional Factorials.

All 16 one-sixteenth fractions of the 2

factorial are related through the generators I = ±124, I = ±135, I = ±236, I =

±1237. The terms remain the same, only the signs are changed for different fractions. The original design (all + signs on

the generators) is called the principal fraction. The remaining 15 are the alternate fractions.

The key point is that, depending on the interpretation of the results of the principal fraction, any one of several other

alternate fractions can be chosen to achieve a particular result when the two fractions are combined. A general strategy

used in running successive experimental designs is to choose judiciously among the members of a given family of

fractional factorials.

Clearly, given the principal fraction, several alternatives are available among the remaining alternate fractions, each

providing a different set of information/effect estimates from the combined design. Table 15 provides some relevant

information concerning the family of fractional factorials associated with a seven-variable experiment using eight-test

designs.

Table 15 family of fractional factorials

Fraction

Generators

When combined with principal

fraction gives:

Principal

I = 124 I = 135 I = 236 I = 1237

. . .

A1 I = -124 I = -135 I = -236 I = -1237

All main effects

I = -124 I = - 135 I = 236 I = -1237

1, 12, 13, 14, 15, 16, 17

I = -124 I = 135 I = -236 I = -1237

2, 12, 23, 24, 25, 26, 27

I = 124 I = -135 I = -236 I = -1237

3, 13, 23, 34, 35, 36, 37

I = -124 I = 135 I = 236 I = 1237

4, 14, 24, 34, 45, 46, 47

I = 124 I = -135 I = 236 I = 1237

5, 15, 25, 35, 45, 56, 57

I = 124 I = 135 I = -236 I = 1237

6, 16, 26, 36, 46, 56, 67

I = 124 I = 135 I = 236 I = -1237 7, 17, 27, 37, 47, 57, 67

Orthogonal Arrays

The theory of fractional factorial designs was first worked out by Finney (Ref 26) and Rao (Ref 27). Many highly

fractionated designs were introduced by Tippett (Ref 28), Plackett and Burman (Ref 29), and others. Some of these were

referred to as magic squares and orthogonal arrays. Two-level and three-level fractional factorial designs gained

widespread attention and industrial application, beginning in the 1950s. Box and Hunter (Ref 7) provided much useful

guidance to the practitioner in the adroit use of these experimental design structures.

In the late 1970s, the use of orthogonal arrays for quality design and improvement by Taguchi (Ref 4) and others gained

widespread acceptance in industry. This has led to considerable discussion concerning the relative merits of these designs

and the methods of design selection vis-à-vis the methodology of the more general class of fractional factorial designs. In

particular, it is important to examine the philosophical framework and interpretation of these similar (often identical)

design structures.

Issue of Confounding. To many, the most significant property of the designs is orthogonality, that is, the ability to

separate out the individual effects of several variables on a response of interest. The term orthogonal arrays as used by

Taguchi implies having this property of orthogonality or producing effects that are not confounded. In fact, whenever

anything less than a full factorial is under consideration, confounding or mixing of effects is present by definition. Such

confounding can only be removed by assumptions made about the physical system and confirmed through some analyses

of the results.

Similarly, when two-level factorials are fractionated, the ability to determine all the interactions among a set of factors is

lost. However, judicious fractionation leads to the ability to obtain knowledge on low-order interactions under the

assumption that higher-order interactions are of negligible importance. Because the orthogonal arrays, as applied to

Taguchi methods, are highly fractionated factorial designs, the information these arrays produce is a function of two

elements: the nature of their confounding patterns and the assumptions made about the physical system they are applied

to. Often, Taguchi's use of linear graphs for design selection fails to produce the highest possible degree of resolution, as

the following example will illustrate.

Example 11: Examination of the Use of an L

) Orthogonal Array

(Ref 4). The notation for various orthogonal arrays by Taguchi and Wu is generally of the following form for designs

without mixing levels L

), where n is number of tests, r is number of levels of each factor, and m is the maximum

number of factors, including selected interactions, that the design can study. For example, L

) refers to a design with

16 tests to study up to 15 two-level factors and/or interactions. An L

) orthogonal array is given in Table 16.

Table 16 An L

) orthogonal array

(a)

A × B

(a)

B × D

(a)

A × D

G D Test

3 4

5 6 7

8 9 10

11 12

13 14

1 1

1 1 1

1 1 1 1 1 1

2 1

1 1

1 1 1

2 2 2 2 2 2 2

3 1

1 2

2 2 2

1 1 1 1 2 2 2

4 1

1 2

2 2 2

2 2 2 2 1 1 1

5 1

2 1

1 2 2

1 1 2 2 1 1 2

6 1

2 1

1 2 2

2 2 1 1 2 2 1

7 1

2 2

2 1 1

1 1 2 2 2 2 1

8 1

2 2

2 1 1

2 2 1 1 1 1 2

9 2

2 1

2 1 2

1 2 1 2 1 2 1

10 2

2 1

2 1 2

2 1 2 1 2 1 2

11 2

2 2

1 2 1

1 2 1 2 2 1 2

12 2

2 2

1 2 1

2 1 2 1 1 2 1

13 2

1 1

2 2 1

1 2 2 1 1 2 2

14 2

1 1

2 2 1

2 1 1 2 2 1 1