ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control
Подождите немного. Документ загружается.


3 - +
-
4 + +
-
5 - -
+
6 + -
+
7 - +
+
8 + + +
Statistical Quality Design and Control
Richard E. DeVor, University of Illinois, Urbana-Champaign; Tsong-how Chang, University of Wisconsin, Milwaukee
Experimental Study Using a 2
3
Factorial Design
Example 8: Use of 2
3
Factorial Design to Determine Need for Preheating or
Postheating of Welded High-Carbon Steel Rail Bars (Ref 23).
High-carbon steel, because of its high strength and low cost, has been extensively used for railway track. The Rail Steel
Bar Association sponsored a research project at the Welding Research Laboratory of the University of Wisconsin around
1960 to study whether or not preheating and postheating were necessary for the high-carbon steel to have good-quality
welds. After a preliminary investigation by manual arc-welding tests, it appeared that there were three variables affecting
the ultimate tensile stress of a weld. Based on the needs of the study and the available funds, it was suggested to run 16
tests that were defined according to a 2
3
factorial design. The three selected variables and their high and low levels are
shown below:
Variable Low level
High level
Ambient temperature (T), °F
0
70
Wind velocity (V), mph 0
20
Bar size (B), in.
4 11
First, the variables are coded such that the high level will be denoted by +1 and the low level by -1. By so doing,
regardless of the physical conditions represented by the two levels, the basic design of any two-level factorial design
becomes a simple arrangement of plus or minus ones. Writing down three columns of the plus and minus ones next to one
another produces the desired 2
3
factorial design, which consists of the 8 distinct sets of coded test conditions, as indicated
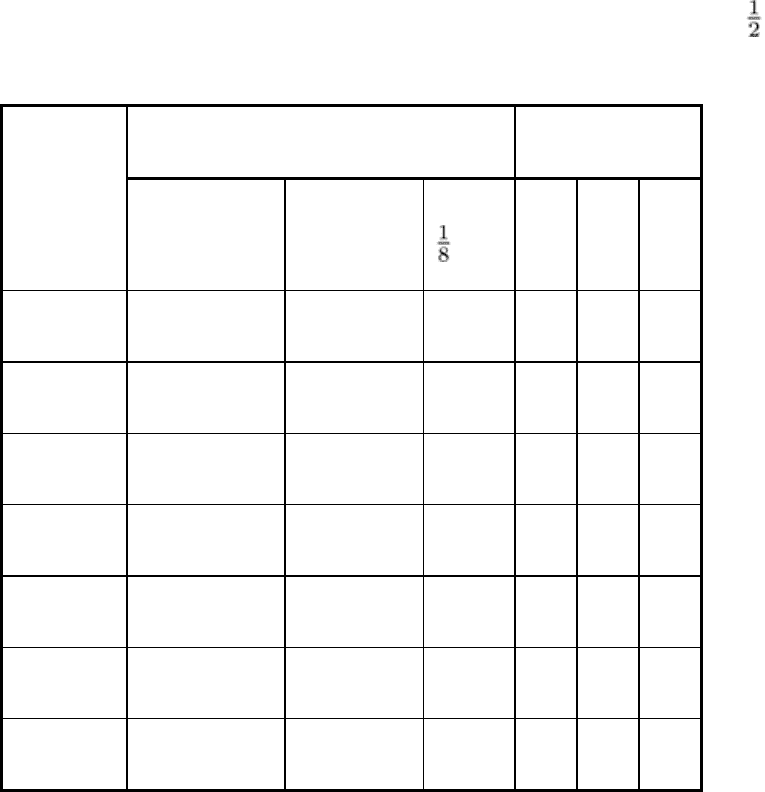
in Table 8. The 8 sets of coded test conditions are given by the 8 rows corresponding to test numbers 1 to 8. These
constitute the recipes for running the tests. For example, the actual welding conditions for test number 1 (which is denoted
by -1, -1, -1) were a temperature of 0 °F, a wind velocity of 0 mph, and a bar size of in.
Table 8 Coded test conditions based on actual test conditions for the steel rail bars of Example 8
Actual test conditions
Coded test conditions
Test number
Temperature, °F
Wind velocity,
mph
Bar size,
in.
X
1
X
2
X
3
1 0 0 4 -1 -1
-1
2 70 0 4 +1 -1
-1
3 0 20 4 -1 +1
-1
4 70 20 4 +1 +1
-1
5 0 0 11 -1 -1
+1
6 70 0 11 +1 -1
+1
7 0 20 11 -1 +1
+1
Geometric Representation of 2
3
Factorial Design. If the three variables are considered to be three mutually
perpendicular coordinate axes X
1
, X
2
, and X
3
, the 2
3
factorial design can be represented geometrically as a cube, as shown
in Fig. 40. The circled numbers at the 8 corner points of the cube represent the corresponding test numbers in standard
order. The 8 actual test conditions are given in brackets. This geometric configuration will be useful later when the
average and interaction effects of the variables are calculated and when the average/main effect and two- and three-factor
interaction effects are interpreted.
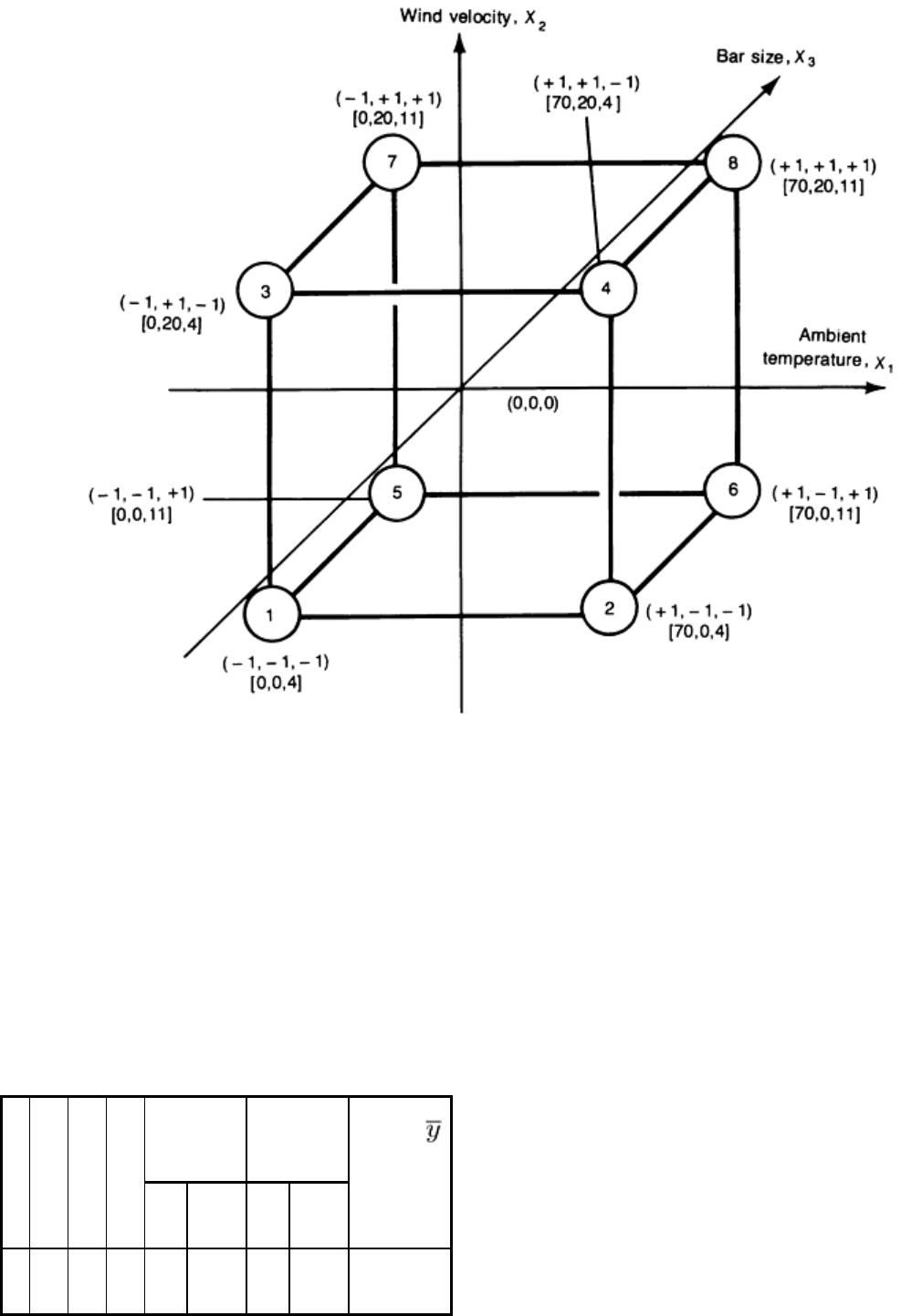
Fig. 40 Geometric representation of the 2
3
factorial design
Test Conduct: Random Order and Replication. In performing experiments, randomization of the test order should
be exercised wherever possible. This is important because the standard order discussed previously is a very systematic
ordering of the tests in terms of the patterns of the levels of the variables from test to test. In this example, there are 8 test
conditions, each of which was replicated once for a total of 16 tests. The main purpose of conducting replicated tests is to
provide an estimate of the experimental error of the test method. The observed responses of these welding experiments
were the ultimate tensile stresses of the welds. Because of replication, 2 responses (y
ai
, y
bi
) were observed at each of the 8
distinct sets of test conditions. Therefore, there were a total of 16 responses (Table 9).
Table 9 Results of the 16 welding experiments for the steel rail bars of Example 8
Because of replication, two responses (y
ai
, y
bi
) were observed for each of the eight distinct sets of test conditions.
Replicate 1
Order of
Replicate 2
Order of
i X
1
X
2
X
3
y
ai
y
ai
y
bi
y
bi
Average,
1
-1 -1 -1 6 84.0 3 91.0
87.5
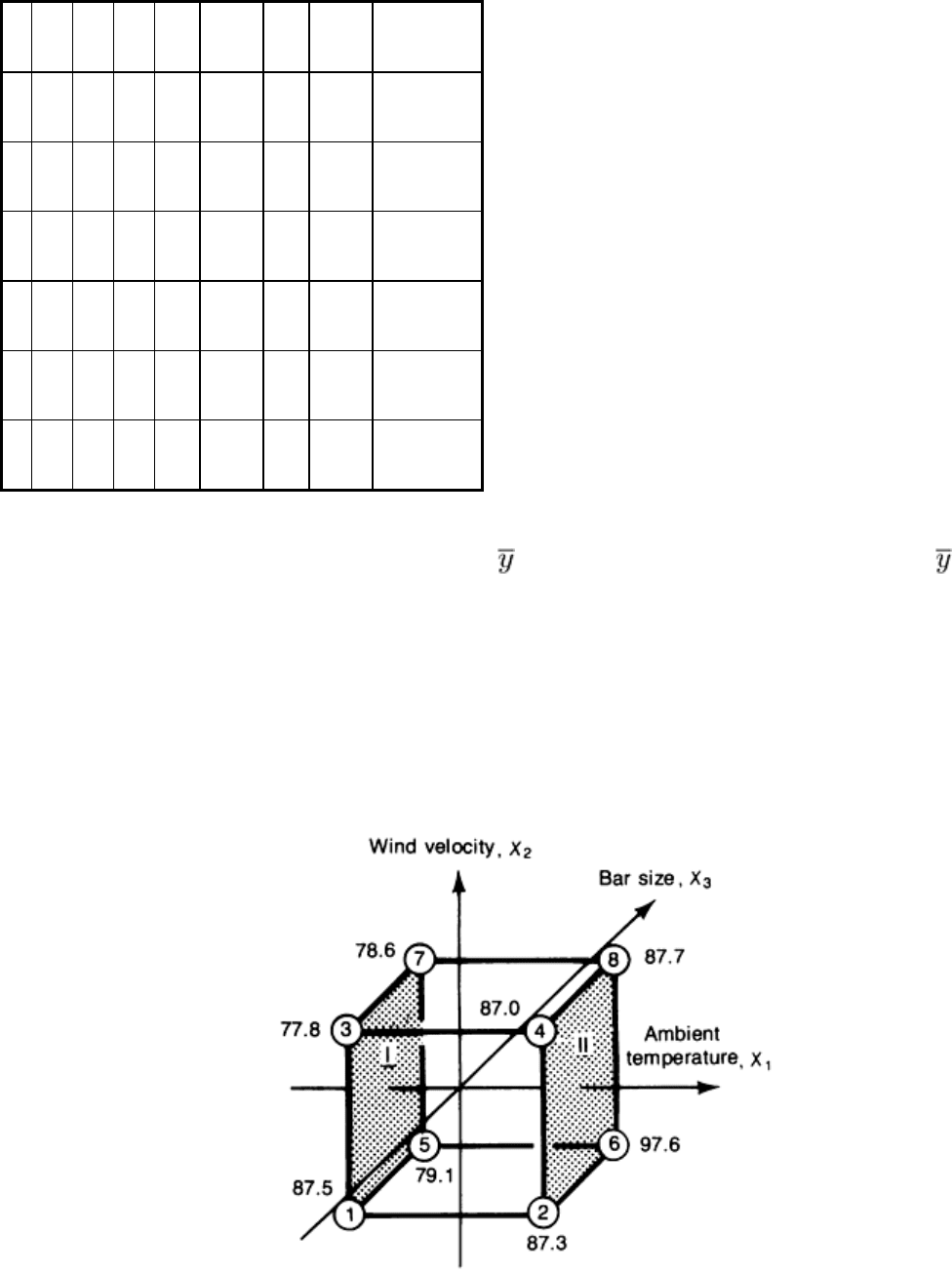
2
+1
-1 -1 8 90.6 7 84.0
87.3
3
-1 +1
-1 1 69.6 5 86.0
77.8
4
+1
+1
-1 2 76.0 4 98.0
87.0
5
-1 -1 +1
5 77.7 8 80.5
79.1
6
+1
-1 +1
3 99.7 1 95.5
97.6
7
-1 +1
+1
4 82.7 2 74.5
78.6
8
+1
+1
+1
7 93.7 6 81.7 87.7
The tests were performed in a random fashion, as indicated by the test order. The average of the 2 responses observed at
each set of test conditions (that is, y
ai
+ y
bi
/2, denoted by
i
) was determined, and the 8 average responses (
i
, where i =
1, 2, . . ., 8) are given in the far right-hand column of Table 9. These average responses will be used to calculate the
average main and average interaction effects for the variables under study.
Calculation of Variable Effects on Weld Strength. Given the results in Table 9, it is possible to evaluate the
individual and joint influences of ambient temperature, wind velocity, and bar size on the ultimate tensile stress of the
weld. To help determine what these variable effects are, what they mean, and how they can be calculated, the geometrical
representation of the experimental design is used. The cube shown in Fig. 41 depicts the 2
3
design geometrically. The
average response (ultimate tensile strength) for each test is given at the corners of the cube.
Fig. 41 Geometric representation of the effect on ultim
ate tensile stress, given at the corners of the cube, of
changes in ambient temperature when wind velocity and bar size are held constant

Calculation of Average Main Effects. As Fig. 41 shows, there are four comparisons of test results or contrasts that
indicate how ultimate tensile stress changes when ambient temperature changes, with wind velocity and bar size being
held constant. The effect of ambient temperature alone can be determined by looking across the cube from left to right.
The differences in the results within each of the 4 pairs of tests reflect the effect of ambient temperature alone on ultimate
tensile stress. The differences in units of ksi are:
• Test No. 1 and 2:
2
-
1
= 87.3 - 87.5 = -0.2
• Test No. 3 and 4:
4
-
3
= 87.0 - 77.8 = 9.2
• Test No. 5 and 6:
6
-
5
= 97.6 - 79.1 = 18.5
• Test No. 7 and 8:
8
-
7
= 87.7 - 78.6 = 9.1
The average effect of ambient temperature, designated by E
1
, is defined as the average of the above four differences. Note
that this average effect is also commonly referred to as a main effect. That is:
E
1
= [(
2
-
1
) + (
4
-
3
) + (
6
-
5
) + (
8
-
7
)]
E
1
= [(-0.2) + (9.2) + (18.5) + (9.1)]
E
1
= 9.15 ksi
Geometrically, the average (main) effect of ambient temperature, E
1
, is the difference between the average test result on
plane II (high level of ambient temperature) and the average test result on plane I (low level of ambient temperature), as
shown in Fig. 41.
The average effect of ambient temperature indicated that, on the average, over the ranges of the variables studied in this
investigation, the effect of changing the ambient temperature from its low level to its high level is to increase the ultimate
tensile stress by 9.150 ksi. However, the individual differences (0.2, 9.2, 18.5, and 9.1 ksi) are actually quite erratic. The
average effect, therefore, must be interpreted with considerable caution because this effect is not particularly consistent
over the four unique combinations of wind velocity and bar size.
Again, referring to Fig. 41, the following pairs of tests can be compared or contrasted to determine the effect of wind
velocity. The average effect of wind velocity, E
2
can be obtained by taking the average of the four individual differences,
which are in units of ksi:
• Test No. 1 and 3:
3
-
1
= 77.8 - 87.5 = -9.7
• Test No. 2 and 4:
4
-
2
= 87.3 - 87.0 = -0.3
• Test No. 5 and 7:
7
-
5
= 78.6 - 79.1 = -0.5
• Test No. 6 and 8:
8
-
6
= 87.7 - 97.6 = -9.9
The value E
2
for tests 1 to 8 is calculated as follows:
E
2
= [(
3
-
1
) + (
4
-
2
) + (
7
-
5
) + (
8
-
6
)]
E
2
= [(-9.7) + (-0.3) + (-0.5) + (-9.9)]
= -5.1 ksi
Similarly, the average effect of bar size, E
3
, is 0.85 ksi.
Interpretation of Average/Main Effects. The average or main effect of a variable has been defined as the amount
of change observed in the response, on the average, when only that variable changes from its low to high value or level. It
is an average effect because within the experimental design there are generally several comparisons or contrasts that can
be made that measure how much the response changes when only a certain variable changes. The sign and the magnitude
of an average/main effect have the following meaning:
• The sign indicates the direction of the effect
• The magnitude indicates the strength of the effect
If the numbers comprising this average are quite similar in magnitude (and of course, sign), the effect of that particular
variable would appear to be independent of the particular level(s) of other variable(s). However, if the numbers
comprising this average are quite different in magnitude (or even sign), the effect of that particular variable depends on
the level(s) that the other variable(s) assumes. In this case, the average/main effect does not hold much significance, and
the response of interest must be examined when two or more variables change simultaneously.
Meaning of Variable Interactions. In calculating the average/main effect of ambient temperature, the amount (and
even direction) of change in weld strength with change in temperature seemed to depend quite heavily on the particular
levels of wind velocity and bar size:
Wind velocity, mph
Bar size, in.
Effect of temperature
on weld strength, ksi
0
-0.2
20
+9.2
0
+18.5
20
+9.1
What is the particular nature of the dependency of the effect of temperature on wind velocity and bar size? The degree of
dependency of the temperature effect on the particular levels of wind velocity and bar size can be appreciated via the
following graphical summaries. Referring to the geometrical representation of the 2
3
factorial in Fig. 41, the interaction
between temperature and wind velocity can be examined by compressing the cube in the bar size direction as shown in
Fig. 42(a). Compressing the cube means that the response values for a given temperature and wind velocity combination--
for example, (-), (-)--are averaged across the high and low levels of bar size. The result is that the cube (Fig. 42a)
becomes a square (Fig. 42b). Similarly, the other two interactions are found to be:
E
13
= [(92.65 - 78.85) - (87.15 - 82.65)]/2
= 4.65 ksi
E
23
= [(83.15 - 82.40) - (88.35 - 87.40)]/2
= -0.10 ksi

Fig. 42 Two-factor interaction between temperature and wind velocity obtained by compressing three-
dimensional cube (a) in the bar size direction to obtain two-dimensional square plane (b)
A Simplified Method for Main and Interaction Effects. Although the geometrical representation of the
experimental design has been quite useful, a simpler and more general method will be needed for calculation of the
variable main and interaction effects. A simplified calculation procedure, which is easily extended for analyzing two-level
factorial designs in any number of variables, is described below.
The mathematical model form associated with a 2
2
factorial is:
Y = b
0
+ b
1
X
1
+ b
2
X
2
+ b
12
X
1
X
2
+ e
where the coefficients b
1
and b
2
correspond to the average/main effects of variables 1 and 2, respectively, and the
coefficient b
12
corresponds to the interaction effect between variables 1 and 2.

Referring to the design matrix for Example 8 (Table 9), estimates of the interaction effects E
12
, E
13
, E
23
, and E
123
can be
obtained by forming the cross-product columns X
1
X
2
, X
1
X
3
, X
2
X
3
, and X
1
X
2
X
3
, as indicated in Table 10. This complete
seven-column matrix will be referred to as the calculation matrix. The cross-product columns of ± signs are simply the
inner-products of the individual columns, for example, X
1
X
2
= (X
1
)(X
2
).
Table 10 Calculation matrix for the data obtained for the steel rail bars of Example 8
Main effects Interactions Test
X
1
X
2
X
3
X
1
X
2
X
1
X
3
X
2
X
3
X
1
X
2
X
3
1 -1 -1 -1 +1 +1 +1 -1
87.5
2 +1
-1 -1 -1 -1 +1 +1
87.3
3 -1 +1
-1 -1 +1 -1 +1
77.8
4 +1
+1
-1 +1 -1 -1 -1
87.0
5 -1 -1 +1
+1 -1 -1 +1
79.1
6 +1
-1 +1
-1 +1 -1 -1
97.6
7 -1 +1
+1
-1 -1 +1 -1
78.6
To calculate any one of the average effects or interactions, merely multiply, element by element, the appropriate column
by the column of average responses, sum algebraically, and divide the sum by 4 (that is, 2
3
/2; in general, for a 2
k
factorial
design, the sum should be divided by 2
k
/2). For example, to calculate the average effect of ambient temperature, E
1
, it is
necessary to proceed as indicated in Table 11. The sum is 36.6 × 10
3
psi or 36.6 ksi, which, when divided by 4, yields
9.150 ksi for the average effect of temperature, the same answer obtained previously.
Table 11 2
k
factorial design calculation of the average effect of ambient temperature on steel rail bar
ultimate tensile strength in Example 8
X
1
i
X
1 i
X
1 i
-1 87.5
(-1) (87.5)
-87.5
+1
87.3
(+1)
(87.3)
+87.3
-1 77.8
(-1) (77.8)
-77.8
+1
87.0
=
(+1)
(87.0)
=
+87.0

-1 79.1
(-1) (79.1)
-79.1
+1
97.6
(+1)
(97.6)
+97.6
-1 78.6
(-1) (78.6)
-78.6
+1
87.7
(+1)
(87.7)
+87.7
Sum
=
+36.6
The two-variable and three-variable interactions can be calculated by the same method (Table 12). For example, to
calculate the interaction between ambient temperature and wind velocity, E
12
, multiply the column X
1
X
2
by the column of
i
, sum algebraically, and then divide the sum by 2
3
/2 = 4. Dividing the sum by 4 yields the answer obtained previously
(namely, 0) for this two-variable interaction.
Table 12 2
k
factorial design calculation of interaction between ambient temperature and wind velocity on
steel rail bar ultimate tensile strength in Example 8
X
1
X
2
i
X
1
X
2
i
X
1
X
2 i
+1 87.5
(+1) (87.5)
+87.5
-1 87.3
(-1) (87.3)
-87.3
-1 77.8
(-1) (77.8)
-77.8
+1 87.0
=
(+1) (87.0)
=
+87.0
+1 79.1
(+1) (79.1)
+79.1
-1 97.6
(-1) (97.6)
-97.6
-1 78.6
(-1) (78.6)
-78.6
+1 87.7
(+1) (87.7)
+87.7
Sum
=
0.0
Judging the Importance of Average Effects. To judge the relative importance of a variable effect based on the
calculated average effects and interactions, it is necessary to make use of the test replications to estimate the error
expected in an effect estimate. In particular, it is necessary to:
• Estimate the experimental error via the variance of an individual observation

• Estimate the error/variance associated
with an average effect and/or interaction effect, either of which is
simply a linear combination (sum) of several individual observations
•
Construct the statistical distribution of effect estimates and examine the range of estimates that could
arise
Figure 43 shows a graphical depiction of what could arise from the above-mentioned test replications. In case 1 (Fig.
43a), the effect estimates could easily arise from a distribution with a mean of zero. In case 2 (Fig. 43b), the implication is
that they could not. The above procedures come under the heading of what is commonly referred to as a statistical test of
significance. The two most common approaches in this regard are the hypothesis-testing method and the confidence
interval method. Additional information is available in Ref 8 and 24.
Fig. 43
Judging the relative importance of a variable effect. (a) Effect not important. (b) Effect important. Open
circles represent effect estimates based on multiple experiment results.
Confidence Interval Method. Each of the 8 tests in Example 8 was replicated once (Table 9), so that there were
actually 16 individual observations on the ultimate tensile stress. The error or variance of each of these 16 observations
will now be estimated. The amount of error in an observation is assumed to be about the same for all observations; that is,
the true variance is the same for all 16 observations, and the observations are independent.
For test 1, the two observations are 84.0 ksi and 91.0 ksi. A sample variance for this test condition, designated as , can
be calculated in the usual way:
In this example, 8 different and completely independent sample variances ( , , . . . ) are calculated, 1 for each
unique test condition. The 8 sample variances are calculated to be:
= 24.50
= 21.78
= 134.48
