ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control

Подождите немного. Документ загружается.

Fig. 16 Revised control charts for Table 2 data with sample 6 and sample 16 data eliminated (both have R

values above UCL in Fig. 15) because they are sources of excess process variability. (a) -chart.(b) R-

chart.

Data now have k = 18, n = 5.

Interpretation of Revised Charts. Again, the R-chart is examined first. No points are now outside the control limits,

and no other unusual patterns of variability appear to be present. The R-chart seems to be in good statistical control.

However, examination of the -chart reveals that there are two points above the upper control limit. The investigation of

these points reveals the fact that these two samples (1 and 11) occurred at 8:00 a.m. and 1:00 p.m., roughly corresponding

to the start-up of the boring machine in the morning and directly after the lunch hour. It was found that the samples were

taken from the first few parts made in each case. Once the machine warmed up (approximately 10 min), the problem

disappeared. It was decided as a standard policy not to initiate production until 10 min after start-up of the machine.

With this special cause identified and the corresponding values removed, the new limits are calculated. The control charts

in Fig. 17 now both show good statistical control. The limits can now be extended, and monitoring of the process can be

continued.

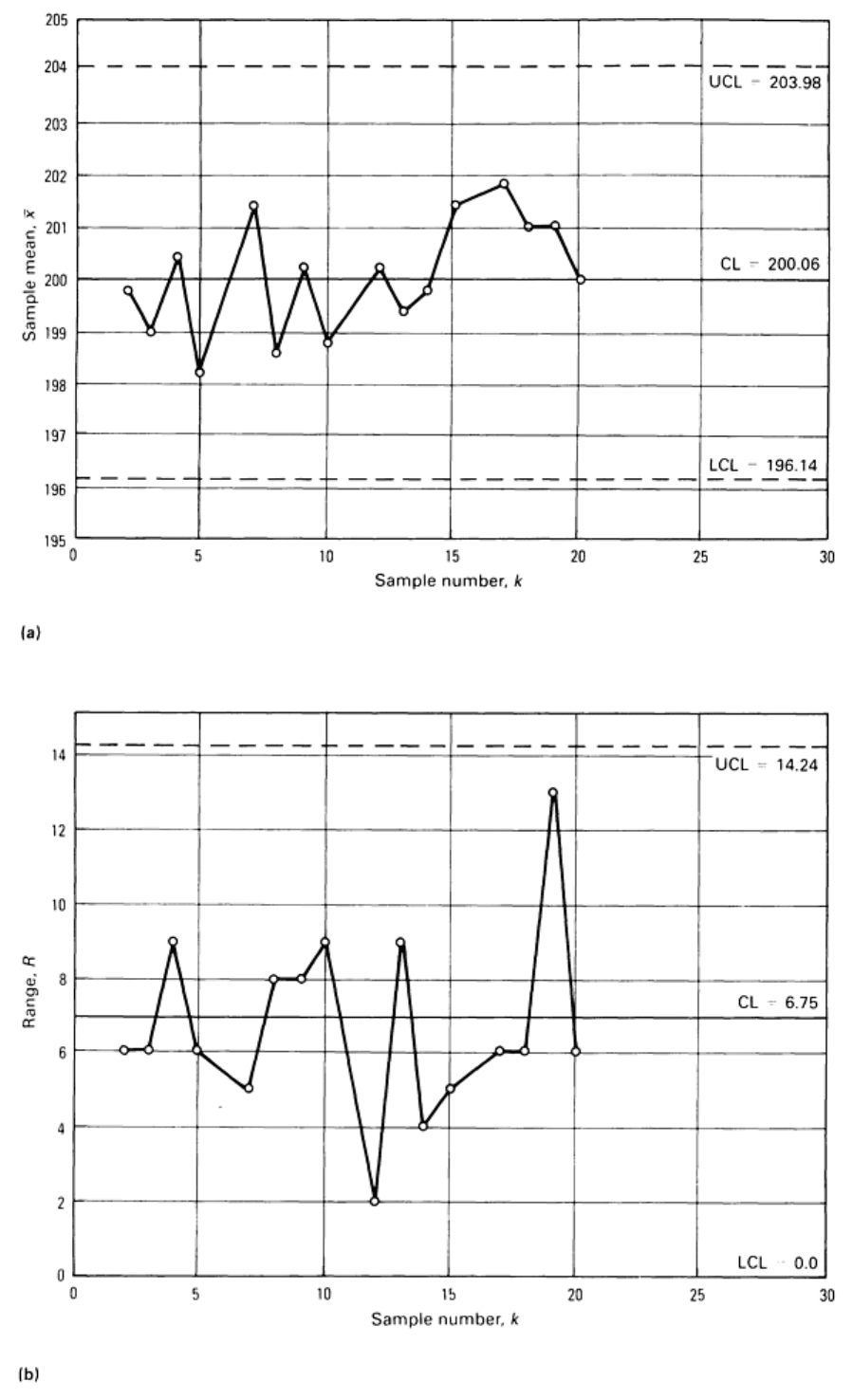
Fig. 17 Second revision control charts for Table 2

data with two more sample deletions (samples 1 and 11,

both of which exceed UCL in Fig. 16

) resulting from workpieces produced prior to machine being properly

warmed up. (a) -chart. (b) R-chart. Data now have k = 16, n = 5.

Importance of Using Both and R Control Charts. This example points to the importance of maintaining both

and R control charts and the significance of first focusing attention on the R-chart and establishing its stability. Initially,

no points fell outside the -chart control limits and one could be led to believe that this indicates that the process mean

exhibits good statistical control. However, the fact that the R-chart was initially not in control caused the limits on the -

chart to be somewhat wider because of two inordinately large R values. Once these special causes of variability were

removed, the limits on the -chart became narrower, and two values now fall outside these new limits. Special causes

were present in the data, but initially were not recognizable because of the excess variability as seen in the R-chart.

This example also points strongly to the need to have 25 or more samples before initiating control charts. In this case,

once special causes were removed, only 16 subgroups remained to construct the charts. This is simply not enough data.

Importance of Rational Sampling

Perhaps the most crucial issue to the successful use of the Shewhart control chart concept is the definition and collection

of the samples or subgroups. This section will discuss the concept of rational sampling, sample size, sampling frequency,

and sample collection methods and will review some classic misapplications of rational sampling. Also, a number of

practical examples of subgroup definition and selection will be presented to aid the reader in understanding and

implementing this central aspect of the control chart concept.

Concept of Rational Sampling. Rational subgroups or samples are collections of individual measurements whose

variation is attributable only to one unique constant system of common causes. In the development and continuing use of

control charts, subgroups or samples should be chosen in a way that provides the maximum opportunity for the

measurements within each subgroup to be alike and the maximum chance for the subgroups to differ from one another if

special causes arise between subgroups. Figure 18 illustrates the notion of a rational sample. Within the sample or

subgroup, only common cause variation should be present. Special causes/sporadic problems should arise between the

selection of one rational sample and another.

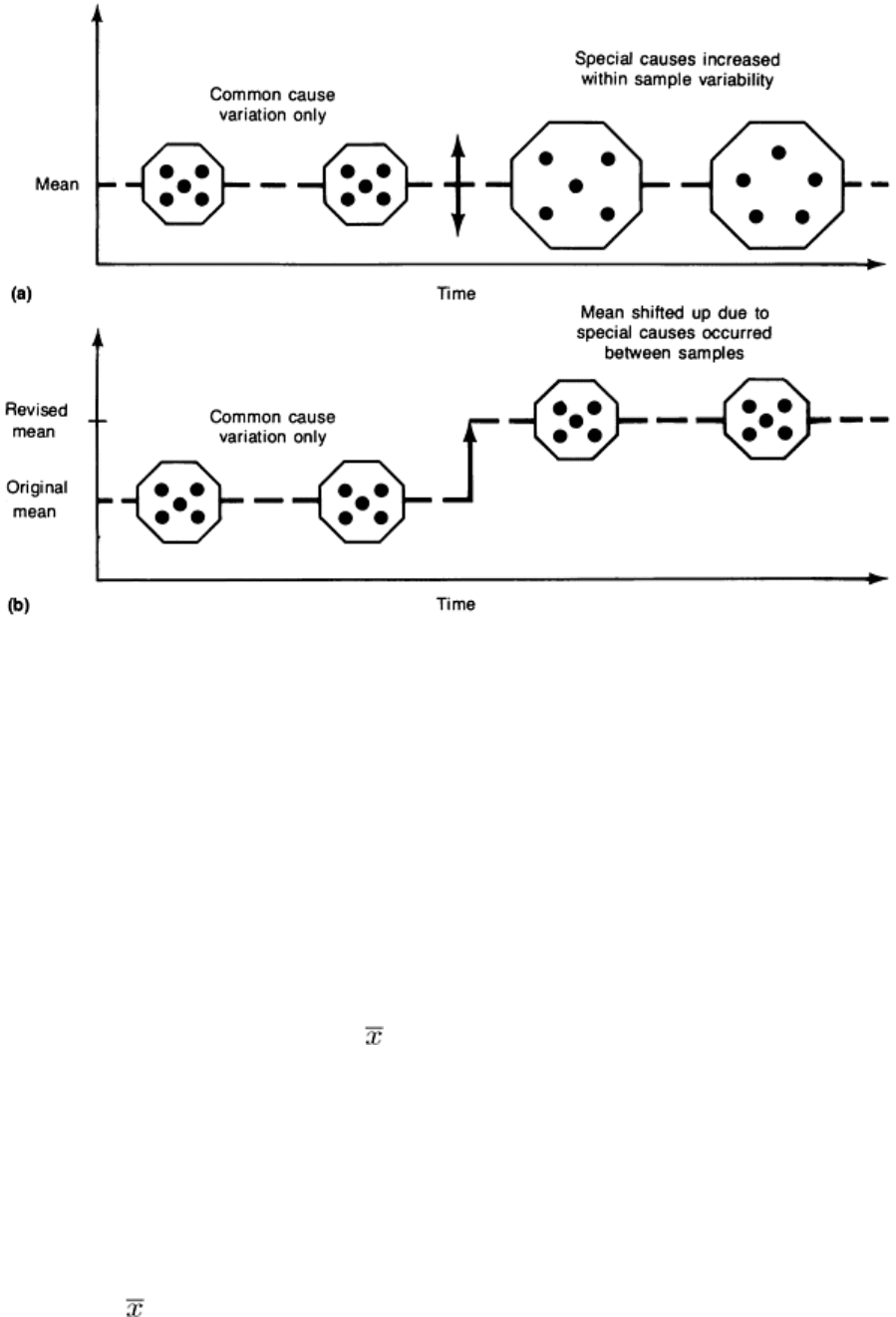
Fig. 18 Graphical depiction of a rational subgroup illustrating effect of special causes on mean.

(a) Unshifted.

(b) Shifted

Sample Size and Sampling Frequency Considerations. The size of the rational sample is governed by the

following considerations:

•

Subgroups should be subject to common cause variation. The sample size should be small to minimize

the chance of mixing data within one sample

from a controlled process and one that is out of control.

This generally means that consecutive sample selection should be used rather than distributing the

sample selection over a period of time. There are, however, certain situations where distributed

sampling may be preferred

•

Subgroups should ensure the presence of a normal distribution for the sample means. In general, the

larger the sample size, the better the

distribution is represented by the normal curve. In practice,

sample sizes of four or more ensure a good approximation to normality

•

Subgroups should ensure good sensitivity to the detection of assignable causes. The larger the sample

size, the more likely that a shift of a given magnitude will be detected

When the above factors are taken into consideration, a sample/subgroup size of four to six is likely to emerge. Five is the

most commonly used number because of the relative ease of further computation.

Sampling Frequency. The question of how frequently samples should be collected is one that requires careful thought.

In many applications of and R control charts, samples are selected too infrequently to be of much use in identifying and

solving problems. Some considerations in sample frequency determination are the following:

• If the process under study has not been charted

before and appears to exhibit somewhat erratic behavior,

samples should be taken quite frequently to increase the opportunity to quickly identify improvement

opportunities. As the process exhibits less and less erratic behavior, the sample interval can be

lengthened

•

It is important to identify and consider the frequency with which occurrences are taking place in the

process. This might include, for example, ambient condition fluctuations, raw material changes, and

process adjustments such as tool changes o

r wheel dressings. If the opportunity for special causes to

occur over a 15-min period is good, sampling twice a shift is likely to be of little value

•

Although it is dangerous to overemphasize the cost of sampling in the short term, clearly it cannot be

neglected

Common Pitfalls in Subgroup Selection. In many situations, it is inviting to combine the output of several parallel

and assumed-to-be-identical machines into a single sample to be used in maintaining a single control chart for the process.

Two variations of this approach can be particularly troublesome: stratification and mixing.

Stratification of the Sample. Here each machine contributes equally to the composition of the sample. For example,

one measurement each from four parallel machines yields a sample/subgroup of n = 4, as seen in Fig. 19. In this case,

there will be a tremendous opportunity for special causes (true differences among the machine) to occur within

subgroups.

Fig. 19 Block diagram depicting a stratified sample selection

When serious problems do arise, for example, for one or more of the machines, they will be very difficult to detect

because of the use of stratified samples. This problem can be detected, however, because of the unusual nature of the -

chart pattern (recall the previous pattern analysis) and can be rectified provided the concepts of rational sampling are

understood.

The R-charts developed from such data will usually show very good control. The corresponding control chart will show

very wide limits relative to the plotted values, and their control will therefore appear almost too good. The wide limits

result from the fact that the variability within subgroups is likely to be subject to more than merely common causes (Fig.

20).

Fig. 20 Typical control charts obtained for a stratified sample selection. (a) -chart. (b) R-chart

Mixing Production From Several Machines. Often it is inviting to combine the output of several parallel

machines/lines into a single stream of well-mixed product that is then sampled for the purposes of maintaining control

charts. This is illustrated in Fig. 21.

Fig. 21 Block diagram of sampling from a mixture

If every sample has exactly one data point from each machine, the result would be the same as that of stratified sampling.

If the sample size is smaller than the number of machines with different means or if most samples do not include data

from all machines, the within-sample variability will be too low, and the between-sample differences in the means tend to

be large. Thus, the -chart would give an appearance that the values are too far away from the centerline.

Statistical Quality Design and Control

Richard E. DeVor, University of Illinois, Urbana-Champaign; Tsong-how Chang, University of Wisconsin, Milwaukee

Zone Rules for Control Chart Analysis

Special causes often produce unnatural patterns that are not as clear cut as points beyond the control limits or obvious

regular patterns. Therefore, a more rigorous pattern analysis should be conducted. Several useful tests for the presence of

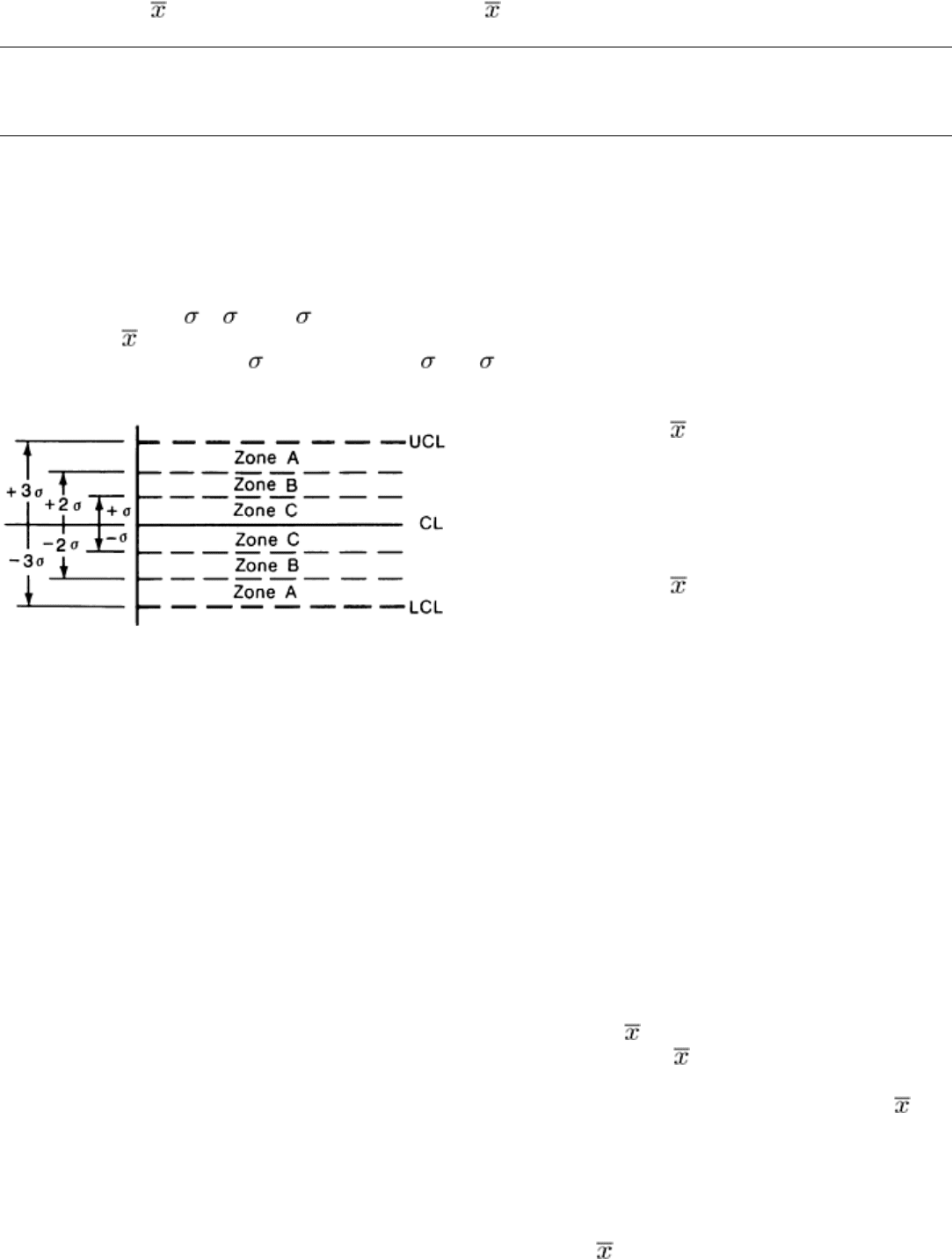
unnatural patterns (special causes) can be performed by dividing the distance between the upper and lower control limits

into zones defined by , 2 , and 3 boundaries, as shown in Fig. 22. Such zones are useful because the statistical

distribution of follows a very predictable pattern--the normal distribution; therefore, certain proportions of the points

are expected to fall within the ± boundary, between and 2 , and so on.

The following sections discuss eight tests that can be applied

to the interpretation of and R control charts. Not all of

these tests follow/use the zones just described, but it is

useful to discuss all of these rules/tests together. These tests

provide the basis for the statistical signals that indicate that

the process has undergone a change in its mean level,

variability level, or both. Some of the tests are based

specifically on the zones defined in Fig. 22 and apply only to

the interpretation of the -chart patterns. Some of the tests

apply to both charts. Unless specifically identified to the

contrary, the tests/rules apply to the consideration of data to

one side of the centerline only.

When a sequence of points on the chart violates one of the

rules, the last point in the sequence is circled. This signifies

that the evidence is now sufficient to suggest that a special cause has occurred. The issue of when that special cause

actually occurred is another matter. A logical estimation of the time of occurrence may be the beginning of the sequence

in question. This is the interpretation that will be used here. It should be noted that some judgment and latitude should be

given. Figure 23 illustrates the following patterns:

• Test 1(extreme points): The existence of a single point beyond zone A signals the presence of an out-of-

control condition (Fig. 23a)

• Test 2 (2 out of 3 points in zone A or beyond):

The existence of 2 out of any 3 successive points in zone

A or beyond signals the presence of an out-of-control condition (Fig. 23b)

• Test 3 (4 out of 5 points in zone B or beyond):

A situation in which there are 4 out of 5 successive points

in zone B or beyond signals the presence of an out-of-control condition (Fig. 23c)

• Test 4 (runs above or below the centerline):

Long runs (7 or more successive points) either strictly

above or strictly below the centerline; this rule applies to both the and R control charts (Fig. 23d)

• Test 5 (trend identification): When 6 successive points on either the or the R co

ntrol chart show a

continuing increase or decrease, a systematic trend in the process is signaled (Fig. 23e)

• Test 6 (trend identification): When 14 successive points oscillate up and down on either the or R

control chart, a systematic trend in the process is signaled (Fig. 23f)

• Test 7 (avoidance of zone C test): When 8 successive points, occurring on either side of the center

line,

avoid zone C, an out-of-

control condition is signaled. This could also be the pattern due to mixed

sampling (discussed earlier), or it could also be signaling the presence of an over-

control situation at the

process (Fig. 23g)

• Test 8 (run in zone C test): When 15 successive points on the -

chart fall in zone C only, to either side

of the centerline, an out-of-

control condition is signaled; such a condition can arise from stratified

Fig. 22 Control chart zones to aid chart interpretation

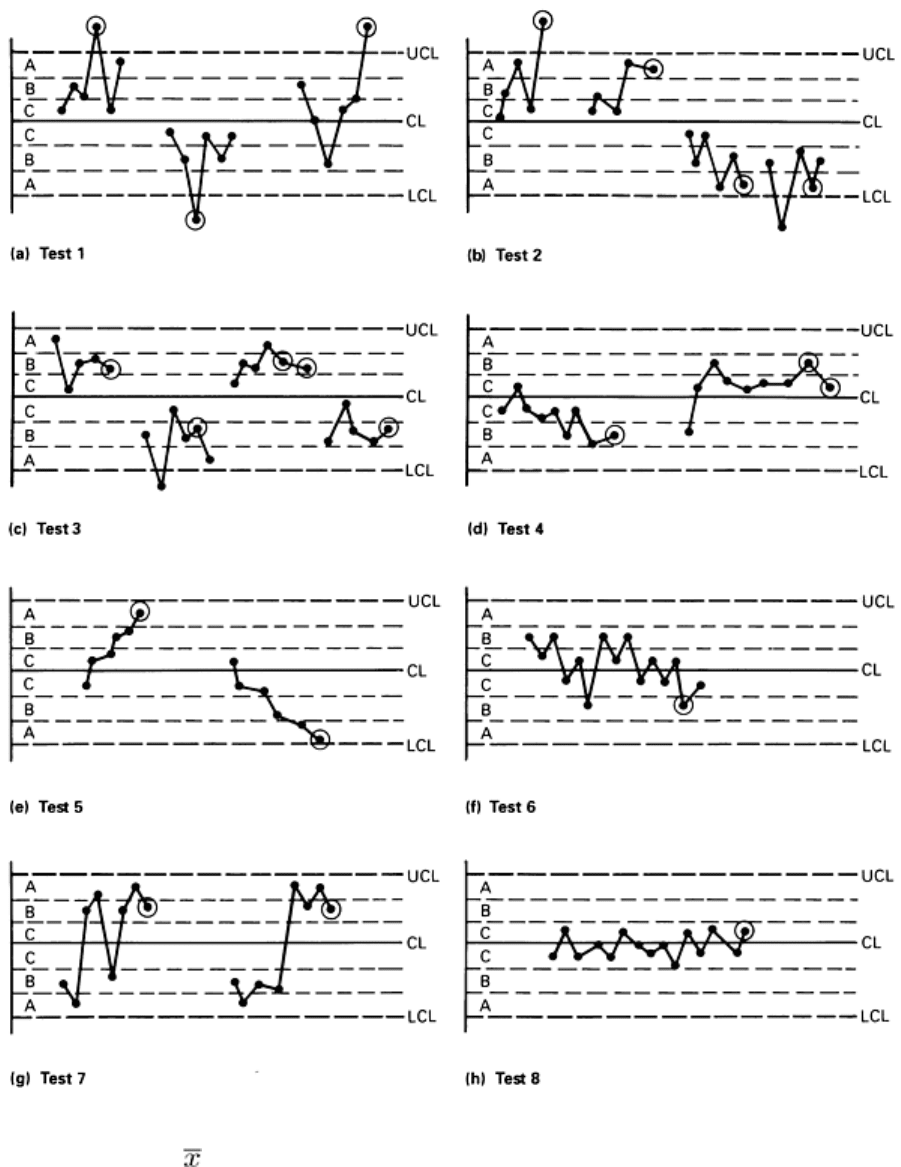
sampling or from a change (decrease) in process variability (Fig. 23h)

The above tests are to be applied jointly in interpreting the charts. Several rules may be simultaneously broken for a given

data point, and that point may therefore be circled more than once, as shown in Fig. 24

Fig. 23 Pattern analysis of -charts. Circ

led points indicate last point in a sequence of points on a chart that

violates a specific rule.

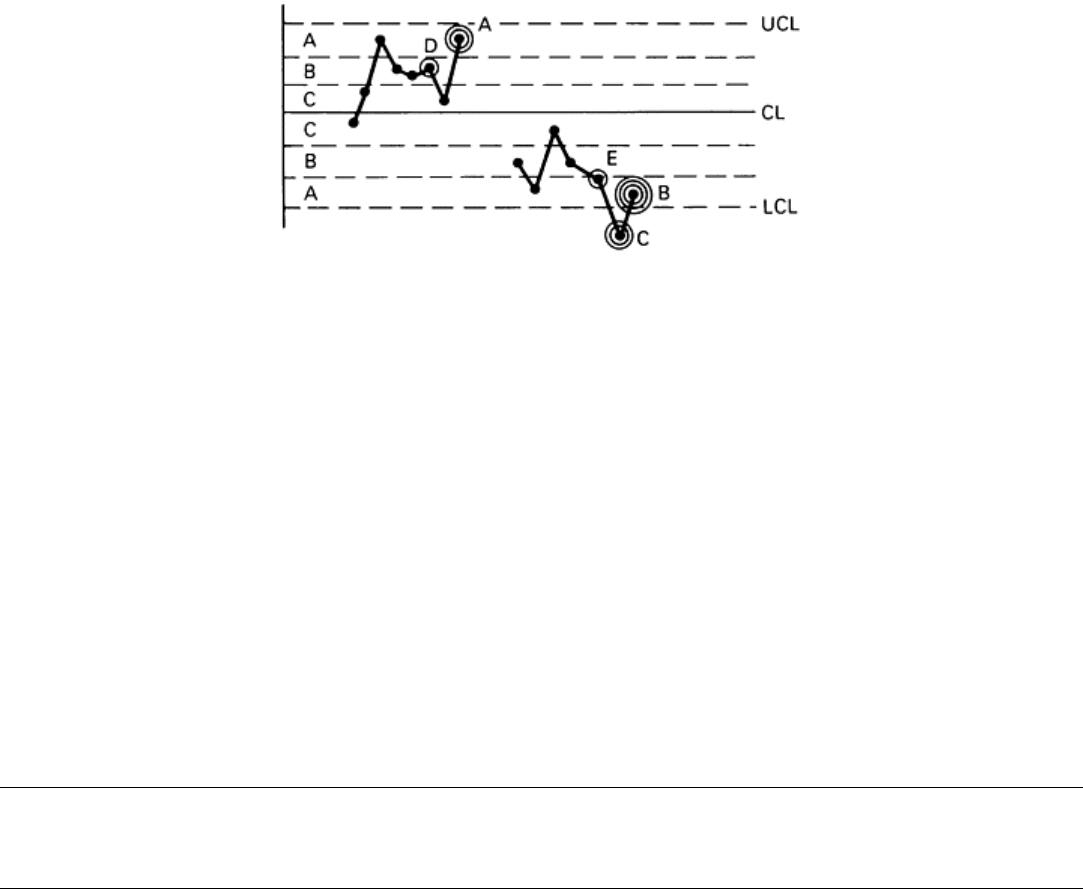
Fig. 24 Example of simultaneous application of more than one test for out-of-

control conditions. Point A is a

violation of tests 3 and 4; point B is a violation of tests 2, 3, and 4; and point C is a violation of tests 1 and 3.

See text for discussion.

In Fig. 24, point A is circled twice because it is the end point of a run of 7 successive points above the centerline and the

end point of 4 of 5 successive points in zone B or beyond. In the second grouping in Fig. 24, point B is circled three times

because it is the end point of:

• A run of 7 successive points below the centerline

• 2 of 3 successive points in zone A or beyond

• 4 of 5 successive points in zone B or beyond

Point C in Fig. 24 is circled twice because it is an extreme point and the end point of a group of five successive points,

four of which are in zone B or beyond. Two other points (D, E) in these groupings are circled only once because they

violate only one rule.

Statistical Quality Design and Control

Richard E. DeVor, University of Illinois, Urbana-Champaign; Tsong-how Chang, University of Wisconsin, Milwaukee

Control Charts for Individual Measurements

In certain situations, the notion of taking several measurements to be formed into a rational sample of size greater than

one simply does not make sense, because only a single measurement is available or meaningful at each sampling. For

example, process characteristics such as oven temperature, suspended air particulates, and machine downtime may vary

during a short period at sampling. Even for those processes in which multiple measurements could be taken, they would

not provide valid within-sample variation for control chart construction. This is so because the variation among several

such measurements would be primarily attributed to variability in the measurement system. In such a case, special control

charts can be used. Commonly used control charts for individual measurements include:

• x, R

control charts

• Exponentially weighted moving average (EWMA) charts

• Cumulative sum charts (CuSum charts)

Both the EWMA (Ref 13, 14, 15, 16) and the CuSum (Ref 17, 18, 19, 20, 21) control charts can be used for charting

sample means and other statistics in addition to their use for charting individual measurements.

x and R

(Moving-Range) Control Charts. This is perhaps the simplest type of control chart that can be used for

the study of individual measurements. The construction of x and R

control charts is similar to that of and R control

charts except that x stands for the value of the individual measurements and R

for the moving range, which is the range

of a group of n consecutive individual measurements artificially combined to form a subgroup of size n (Fig. 25). The

moving range is usually comprised of the largest difference in two or three successive individual measurements. The

moving ranges are calculated as shown in Fig. 25 for the case of three consecutive measurements used to form the

artificial samples of size n = 3.

Fig. 25 Examples of three successive measurements used to determine the moving range

Because the moving range, R

, is calculated primarily for the purpose of estimating common cause variability of the

process, the artificial samples that are formed from successive measurements must be of very small size to minimize the

chance of mixing data from out-of-control conditions. It is noted that x and R

are not independent of each other and that

successive sample R

values are overlapping.

The following example illustrates the construction of x and R

control charts, assuming that x follows at least

approximately a normal distribution. Here, R

is based on two consecutive measurements; that is, the artificial sample

size is n = 2.

Example 2: x and R

Control Chart Construction for the Batch Processing of

White Millbase Component of a Topcoat.

The operators of a paint plant were studying the batch processing of white millbase used in the manufacture of topcoats.

The basic process begins by charging a sandgrinder premix tank with resin and pigment. The premix is agitated until a

homogeneous slurry is obtained and then pumped through the sandgrinder. The grinder output is sampled to check for

fineness and gloss. A batch may require adjustments by adding pigment or resin to achieve acceptable gloss. Through

statistical modeling of the results of some ash tests, a quantitative method was developed for determining the amount of

pigment or resin to be added when necessary, all based on the weight per unit volume (lb/gal.) of the batch. Therefore, it

became important to monitor the weight per unit volume for each batch to achieve millbase uniformity. Table 3 lists

weight per unit volume data for 27 consecutive batches.

Table 3 x and R

control chart data for the batch processing of white millbase topcoat component of

Example 2

Batch

x, lb/gal. R

(a)

1 14.04

2 13.94 0.10 (14.04 - 13.94 = 0.10)

3 13.82 0.12 (13.94 - 13.82 = 0.12)

4 14.11 0.29 (14.11 - 13.82 = 0.29)