ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control
Подождите немного. Документ загружается.


Fig. 12
Impact of having process initially in a state of statistical control versus improvement resulting from a
breakthrough in performance
Fundamental Purposes of Shewhart Control Charts
There are two fundamental purposes that Shewhart control charts can serve:
•
As a tool to provide a sound economic basis for making a decision at the machine regarding whether to
look for trouble, adjust the process, or leave the process alone
• As a mea
ns of assisting in the identification of both improvement opportunities through the detection of
sporadic and chronic faults in the process and to help provide the basis to formulate corrective and
improvement actions
Although these two purposes may appear to be essentially the same, they are not. The former is strictly an on-line activity,
while the latter is an off-line activity. On line, the operator can only recognize and take action against the presence of
special causes of variation. If the process, as monitored on line, is free of special causes, the operator is doing the best that
he can. In short, if the process is in statistical control, the operator should do nothing at all to disturb the routine behavior
of the process.
On the other hand, the fact that the process is in statistical control in no way guarantees that it is a capable process (able to
meet customer expectations as they may be communicated through a specification). However, the operator cannot be
expected to be responsible for this, though he may have some valuable insight into the problem. A lack of process
capability is basically a product/process design and planning problem.
For the techniques of statistical process control (specifically Shewhart control charts) to be successfully employed as an
off-line problem identification and problem-solving tool, it is essential to keep in mind that it is a three-step process, as
follows:
• Use statistical signals to find improvement opportunities through the identification of process faults
• U
se experience, technical expertise, and fault diagnosis methods to find the root cause of the fault that
has been identified
•
Develop an action plan to correct the fault in a manner that will enable any gains that are realized to be
held
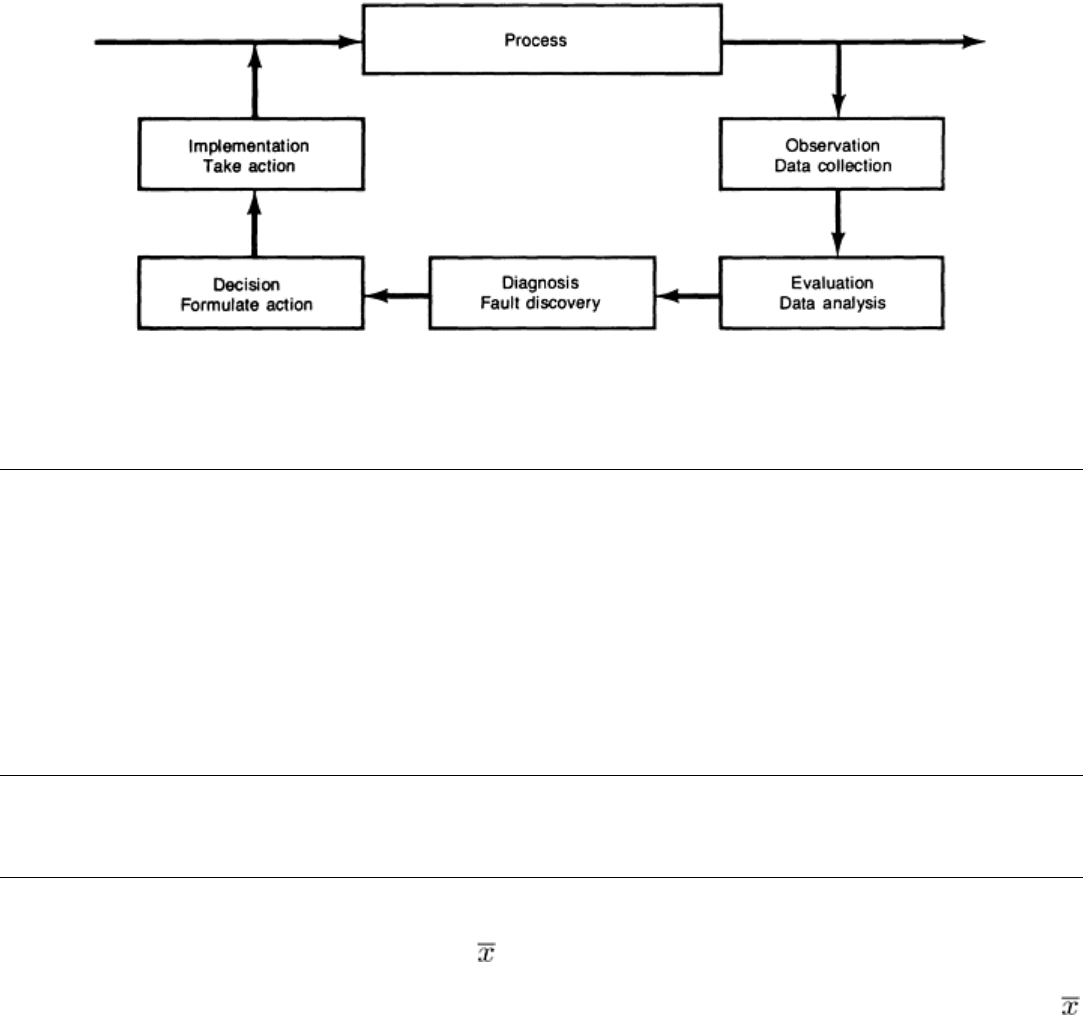
This three-step process can be explained by using the classical feedback control system perspective, as shown in Fig. 13.
There are five distinct stages in the generic control loop shown in Fig. 13. These five stages facilitate the three-step
process in the following way:
• Step 1: Use of statistical signals (observation and evaluation)
• Step 2: Fault diagnosis (diagnosis)
• Step 3: Action plan (decision and implementation)
Fig. 13 Classical feedback control system view of statistical process control implementation
References cited in this section
4. G. Taguchi and Y. Wu, Introduction to Off-Line Quality Control, Central Jap
an Quality Control
Association, 1979
10.
W.A. Shewhart, The Economic Control of Quality of Manufactured Product,
Van Nostrand, 1931 (ASQC,
1980)
11.
W.E. Deming, Quality, Productivity, and Competitive Position,
MIT Center for Advanced Engineering,
1982
12.
J.M. Juran, Quality Problems, Remedies, and Nostrums, Ind. Qual. Con., Vol 22, 1966, p 647-653
Statistical Quality Design and Control
Richard E. DeVor, University of Illinois, Urbana-Champaign; Tsong-how Chang, University of Wisconsin, Milwaukee
Construction and Interpretation of and R Control Charts
This section focuses on the construction and interpretation of Shewhart control charts for variable data, in particular,
and R control charts. All the necessary equations and procedures for the calculation and graphical representation of the
basic elements of the charts are presented. In addition, this section presents some probabilistic rules to aid in the
interpretation of these charts.
Shewhart Control Chart Model

The control chart stands much as a jury in a court of law. The information from each sample is judged in order to
determine whether or not it indicates the presence of a special cause disturbance. Unless the evidence is overwhelmingly
in favor of the occurrence of a special cause disturbance, a verdict of not guilty is entered. In other words, there is no
strong reason to believe that forces other than those of common causes are at work. Such an interpretation is, in fact,
based on and consistent with the hypothesis-testing approach to making statistical inferences about the population/process
based on information contained in the sample.
If a process under surveillance by periodic sampling maintains a state of good statistical control, this means that its mean
level and level of variability remain constant over time. If such is the case, the sample means would have a distribution
that follows the normal distribution, and nearly all the sample means would fall within the band of plus or minus three
standard deviations of , or ±3σ , where σ is the standard deviation of about the established process average. Because
the chance of realizing a point outside the 3σ limits is so small if good statistical control is evident, the occurrence of
such a sample result must be interpreted as signaling some special/sporadic departure from expected behavior; that is,
something other than common cause variation must be present. Figure 14 illustrates the presence of such a special cause.
The 3σ limits about the process average/centerline are referred to as the upper control limit (UCL) and the lower control
limit (LCL).
Fig. 14 Use of probabilistic limits to identify unusual process behavior over a period of time
Suppose a sample mean, , falls above the upper control limit. Because the chance of this occurring is so small (about
of 1%) if the process mean is truly at the centerline, it must be assumed that some special cause is present that shifted the
process mean to a different level. Unfortunately, the fact that all points fall within the 3 limits does not mean that
special causes are not present. Departures from expected process behavior may not always manifest themselves on the
control chart immediately or for that matter at all. Although narrower limits (for example, 2σ limits) would allow easier
and faster detection of special causes, such limits would also increase the chances of false alarms, that is, times when the
process is actually in good statistical control but a sample mean, , falls outside the control limits.
Appropriate placement of the upper and lower control limits is an economic issue. The intent would be to fix the limits in
such a way as to balance the economic consequences of failing to detect a special cause when it does occur and wrongly
identifying the presence of a special cause when it has really not occurred. Experience has led to the use of 3σ limits as
a good balance of these risks.
Generally, chaotic disturbances manifest themselves in two possible ways:
• Shifts or changes in the mean level of the process
• Shifts or changes in the amount of process variability
Figure 14 represents only one side of the coin; thus, a fundamental rule has been violated--that an -chart should not be
shown without the associated range chart. By monitoring the process through sampling, the sample mean, , can be used

to aid in determining when a change in the mean level has occurred. By determining the range, R, for each sample and
tracking its behavior over time, a basis is provided for identifying the presence of changes in process variability.
Establishing a control chart for ranges R comparable to the -chart requires more specific information about the
distribution of the process. In particular, it will be assumed that the individual measurements x are normally distributed.
Doing so establishes the relationship between the standard deviation of ranges R and the standard deviation of individual
process observations or measurements.
For simplicity, ±3
R
limits will be placed about the average range to define the upper and lower control limits for R
even though the frequency distribution of ranges is not a symmetric distribution. Obtaining σ
R
will be discussed later in
this article.
Setting Up and R Control Charts. Once the statistical basis for Shewhart control charts has been established, it
remains to define the necessary elements of the charts mathematically and to establish a standard graphical representation.
This section deals with the construction of and R control charts. All the necessary equations and general procedures for
the calculation and graphical representation of the basic elements of the charts are presented in this section.
The first step in setting up and R control charts is the selection of the samples. It is important that all samples be rational
samples. Rational samples are groups of measurements whose variation is attributable only to one constant system of
common cause. Sampling from different machines, sampling over extended periods of time, and sampling from product
combined from several sources are all nonrational sampling methods and must be avoided. Rational samples will be
discussed in more detail later in this article.
As a rule of thumb, 25 to 50 samples should be selected to provide a solid basis for the initiation of the control charts.
This will help to ensure more precise estimation of the process mean and standard deviation. The sample/subgroup size
should be relatively small (between n = 3 and n = 6).
With k rational samples of n each, the following steps can be used as a guide when constructing , R control charts with
3 limits:
• Calculate the sample mean and sample range for each sample using = x/n and R = x
max
- x
min
• Calculate the grand mean of the n sample means and the average range using = /k and = R/k
• Calculate the control limits for the R-
chart. Although the true distribution of sample ranges is not
normal and not symmetric, the symmetric limits are conventionally used for the R-
charts. With assumed
normal distribution for the individua
l measurements, the following formulas can be used for the
calculation of the control limits: UCL
R
= D
4
and LCL
R
= D
3
• Calculate the control limits for the -chart. Although the
required standard deviation (the standard
deviation of the sample mean, ) for setting the limits is
x
, this value is conveniently estimated by
/(d
2
), where d
2
is a function of n. For 3 limits, one uses a factor called A
2
, which is equal to
3/(d
2
) and can be found in Table 1. Thus, the control limits are calculated by: UCL
x
= + A
2
and
LCL
x
= - A
2
The appropriate values for d
2
, A
2
, D
3
, and D
4
are obtained from Table 1.
Table 1 Factors for and R control chart limits
Factors for control limits
R-chart
Sample
size, n
-chart
A
2
D
3
D
4
Factor for
calculating
σ
x
from
range, R
d
2

2 1.880 0 3.267
1.128
3 1.023 0 2.573
1.693
4 0.729 0 2.282
2.059
5 0.577 0 2.114
2.326
6 0.483 0 2.004
2.534
7 0.419 0.076
1.924
2.704
8 0.373 0.136
1.864
2.847
9 0.337 0.184
1.816
2.970
10 0.308 0.223
1.777
3.078
11 0.285 0.256
1.744
3.173
12 0.266 0.283
1.717
3.258
13 0.249 0.307
1.693
3.336
14 0.235 0.328
1.672
3.407
15 3.472 0.223
0.347
1.653
16 0.212 0.363
1.637
3.532
17 0.203 0.378
1.622
3.588
18 0.194 0.391
1.608
3.640
19 0.187 0.403
1.597
3.699
20 0.180 0.415
1.585
3.735
Example 1: Construction of and R Control Charts of an Engine Block Cylinder Bore.
The inside diameter of the cylinder bore in an engine block was measured after a boring operation. Measurements were
made to 0.0001 in. Samples of size n = 5 were taken to obtain some data to initiate and R control charts for this process.
The samples were taken roughly every h. The sample measurements were all taken on the same number cylinder in the

block. The results of the first 20 samples are given in Table 2. The actual measurements are of the form 3.5205 in., 3.5202
in., and so on. Table 2 provides only the last three digits in the measurement.
Table 2 and R control chart engine block cylinder boring process data of Example 1
Individual measurements, x
(a)(b)
Sample number, k
1 2 3 4 5
(b)
R
(b)
1 205 202 204 209 205 205 7
2 202 196 201 198 202 199.8
6
3 201 202 199 197 196 199 6
4 205 203 196 201 197 200.4
9
5 199 196 201 200 195 198.2
6
6 203 198 192 217 196 201.2
25
7 202 202 198 203 202 201.4
5
8 197 196 196 200 204 198.6
8
9 199 200 204 196 202 200.2
8
10 202 196 204 195 197 198.8
9
11 206 204 202 210 205 205.4
8
12 200 201 199 200 201 200.2
2
13 205 196 201 197 198 199.4
9
14 202 199 200 198 200 199.8
4
15 200 200 201 205 201 201.4
5
16 201 187 209 202 200 199.8
22
17 202 202 204 198 203 201.8
6
18 201 198 204 201 201 201 6
19 207 206 194 197 201 201 13
20 200 204 198 199 199 200 6
(a)
Sample/subgroup size, n = 5.
(b)
Although actual cylinder bore data ranged from 3.5187 to 3.5217 in., only the last three digits in the measurement for x, , and R are
used.
Determination of Trial Control Limits. Based on these first 20 samples, each sample mean and R was calculated
as listed in the last two columns of Table 2. The grand average, , and average range, , are = 200.62 and = 8.5.
For -chart:
UCL = + A
2
= 200.62 + (0.58) (8.5) = 205.55
LCL = - A
2
= 200.62 - (0.58) (8.5)
= 195.69
For R-chart:
UCL = D
4
= 8.5 (2.11) = 17.935
LCL = D
3
= 8.5 (0) = 0.0
With the above calculations completed, the and R control charts can be constructed. It will be important to start with the
R-chart and to get it under statistical control first. This is necessary because the limits of the -chart depend on the
magnitude of the common cause variation of the process measured by . If initially some points on the -chart exceed
the upper control limit (special causes present), the limits in the -chart will be inflated and will need to be recalculated
after such special cause data are removed.
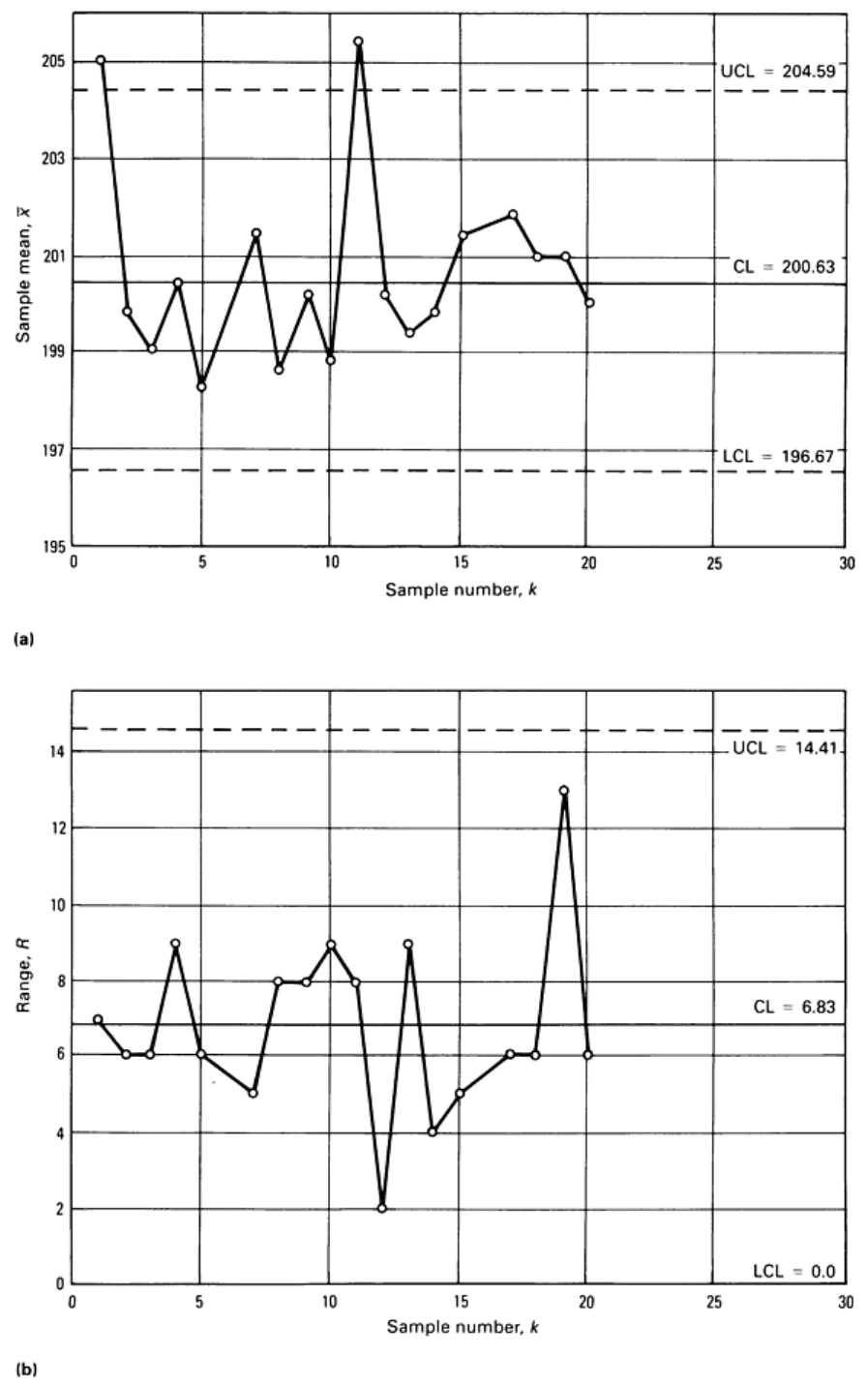
Interpretation of Initial Charts. Figure 15 shows the and R control charts based on the calculations given above.
The R-chart is examined first, and it is found that two points exceed the 3 limit. This indicates that there are special
causes (excess process variability) at least at these points. These points--samples 6 and 16--are then examined to identify
the reasons for these special causes. The records show that at these points the regular operator was absent and a less-
experienced relief operator ran the production for a short time. As a result, samples 6 and 16, taken over the time the relief
operator ran the process, exhibited greater variability, perhaps because of inexperience. Because special causes can be
identified for samples 6 and 16, these sample values (both and R) are removed and new limits are calculated. The
revised centerlines and limits for and R control charts based on the data after samples 6 and 16 have been deleted are
shown in Fig. 16.
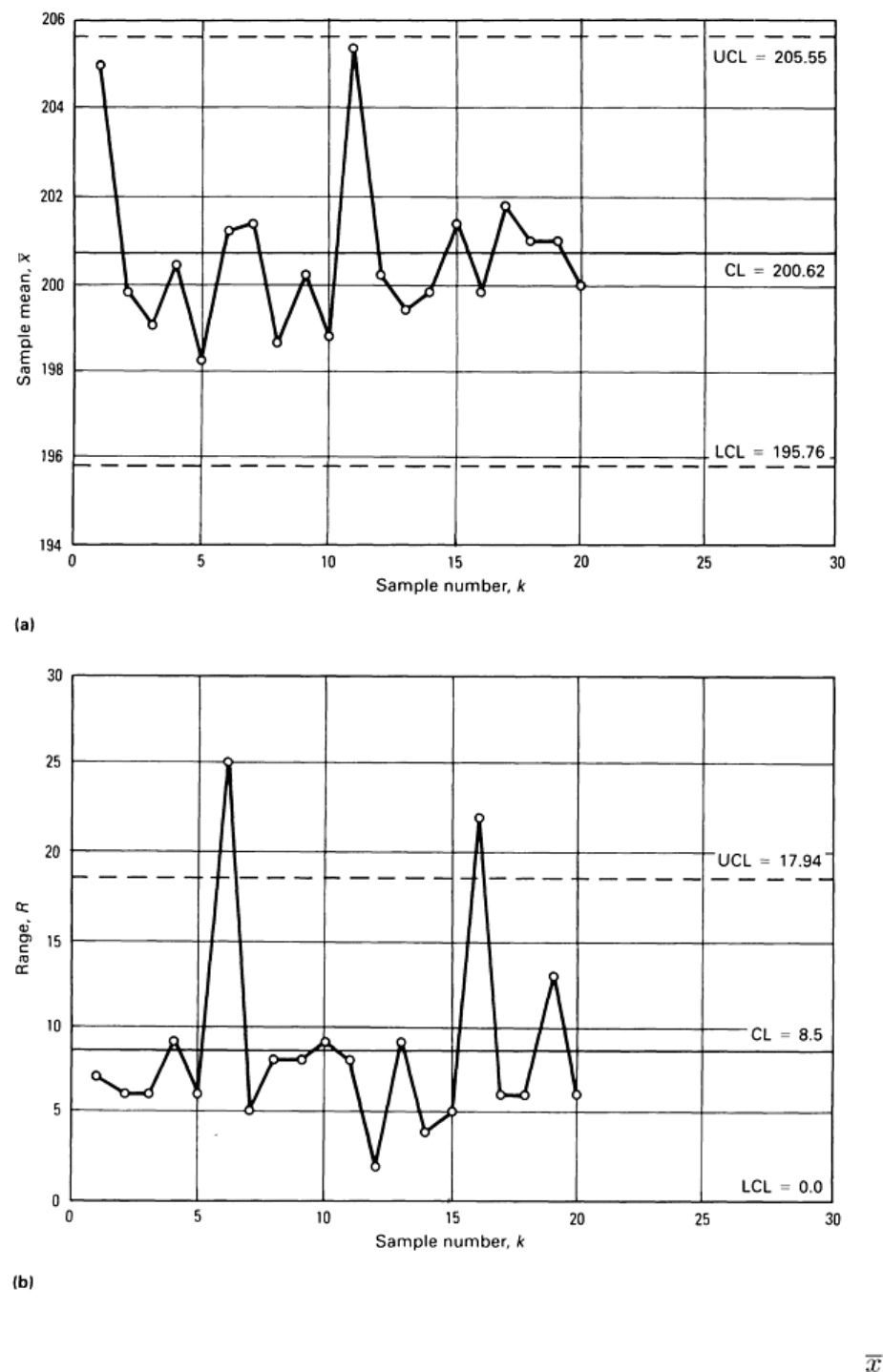
Fig. 15 Control charts for inside diameter measurements of engine block cylinder bores in Table 2. (a) -
chart.
(b) R-chart. Data are for k = 20, n = 5.