ASM Metals HandBook Vol. 14 - Forming and Forging
Подождите немного. Документ загружается.

It follows that the rate of entropy production by the system is given by:
(Eq 45)
where P/T can be thought of as the applied rate of entropy input
app
.
According to the second law of thermodynamics, s should be greater than unity for stable material flow. This implies that
the workpiece should store entropy at least as fast as the entropy production rate of working heat for stable flow.
Therefore, s/ (log ) should also be less than 0 for stable flow if s is treated as a Liapunov function, that is:
V
2
= s (log )
(Eq 46)
These two conditions-- / (log ) < 0 and s/ (log ) < 0--are important and are used for the development of
processing maps.
The processing map provides the necessary conditions for working a material under stable processing conditions. It
represents a conservative estimate of the conditions in terms of T and . However, it is necessary to examine the effective
stress rate path, which is determined by process modeling, to determine whether instability can be caused by such
processes as grain-boundary cavitation or wedge cracking when the processing conditions are marginal. A value of
m
/
of corresponds to a pure tensile state of stress.
Under this condition, any deformation process leading to cavity nucleation would eventually produce ductile fracture.
When
m
/ is equal to - , large amounts of plastic flow are possible. This state of stress corresponds to conditions that
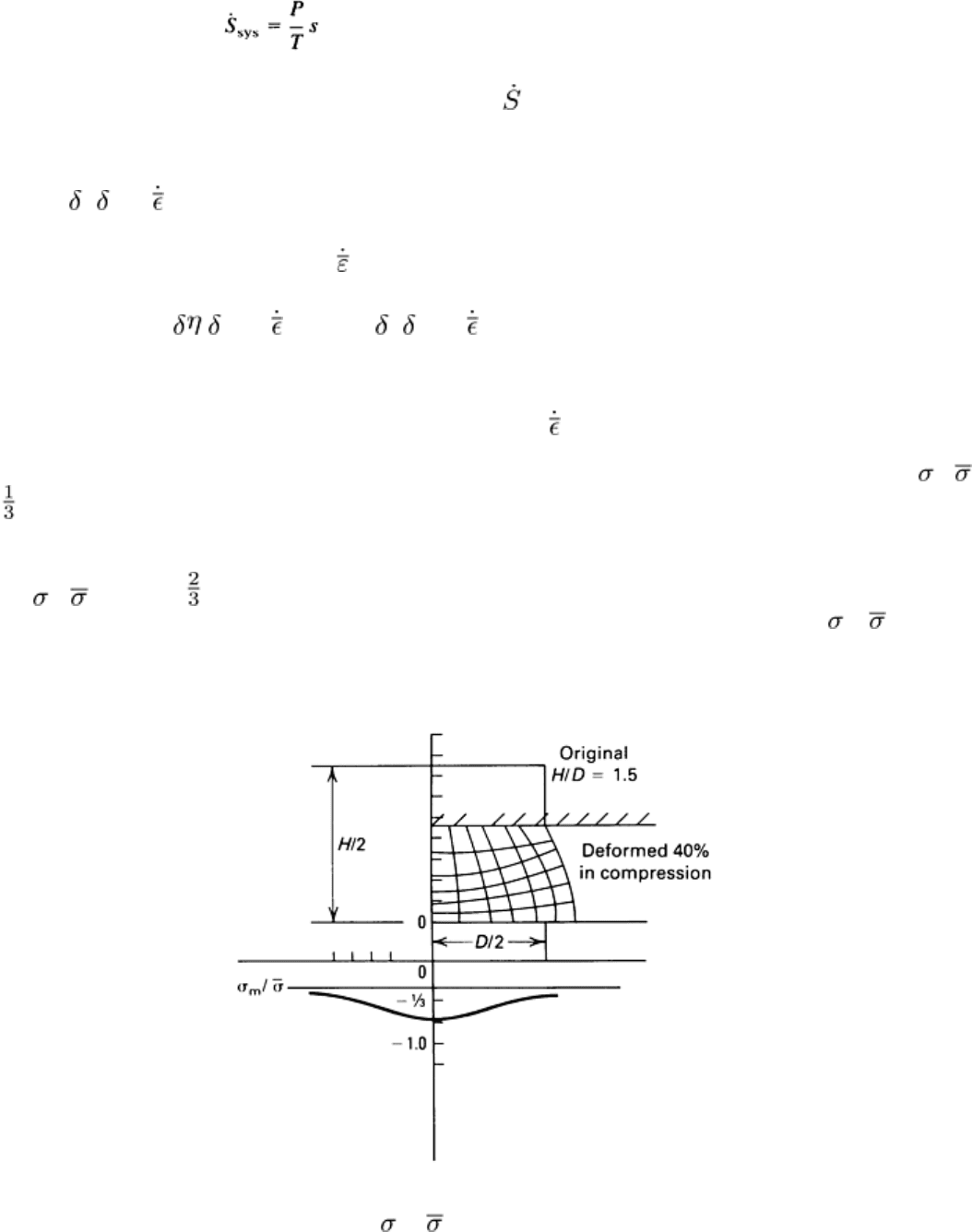
can be associated with ideal streamlined flow during extrusion. Figure 7 shows the distribution of
m
/ during the
uniaxial compression of a cylindrical rod, and Fig. 8 shows plane-strain compression. Both of these are under conditions
of high friction.
Fig. 7 Mesh distortion and distribution of
m
/ during uniaxial compression (from finite-
element method
analysis)
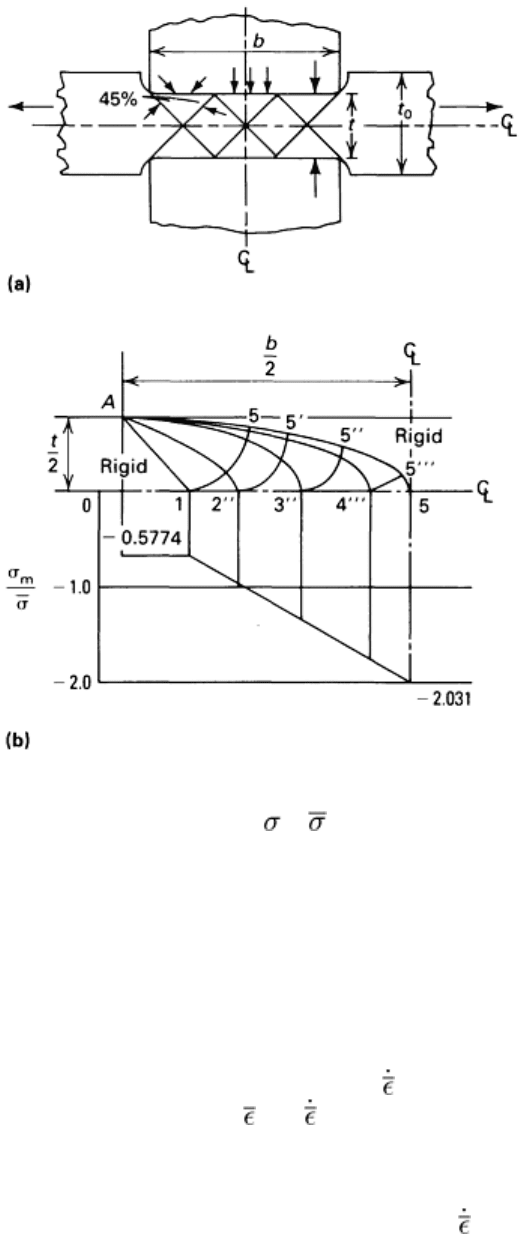
Fig. 8 Slip line field (a) and distribution of
m
/ (b) during plane-strain compression
Intrinsic Workability
Materials being formed (forged) undergo large, nonlinear, irreversible deformation that is made possible by linking
together several atomic processes. This string of processes, in addition to providing the degree of freedom needed for
producing large deformation, is also responsible for the evolution of structure. Each of these processes can be thought of
as a channel for dispersing energy supplied by the forging process, and each can give rise to entropy production. Forging,
as a rule, is a shape-changing process in which the deformation is generally inhomogeneous and transient over a large
volume of the deforming continuum. Steady-state phenomena often represent a limiting condition that can be achieved
only under unique combinations of temperature T and effective strain rate . Therefore, it is highly desirable to be able to
define stable regions in terms of the kinematic variables T, , and .
A solution to this problem would require identification of the limiting conditions. These limiting conditions would be loci
of bifurcation points where two atomic mechanisms are operating simultaneously to produce a maximum in the energy
dispersal rate at a unique combination of temperature T and effective strain rate . Under these unique conditions, the
deformation process would be steady state. One branch of the deformation process would be stable, and the other would
be unstable. Processes such as grain-boundary cavitation, wedge cracking, and cleavage are considered to cause the
deforming continuum to become unstable, because the free surfaces formed increase the free energy of the system rather
than decrease it. Therefore, workability is an intrinsic characteristic of the material; the ability of the material to dissipate
power at any state of stress by favorable metallurgical mechanisms generates entropy at a faster rate than it is applied and
maintains the total energy of the system at the lowest level possible.
Determination of Processing Maps
Using flow stress values calculated at different temperatures and effective strain rates, the parameters and s are
determined as functions of temperature and effective strain rate. From these values, / (log ) and s/ (log ) values
are calculated, and all the values less than or equal to 0 are grouped to determine the stable region. The stable region and
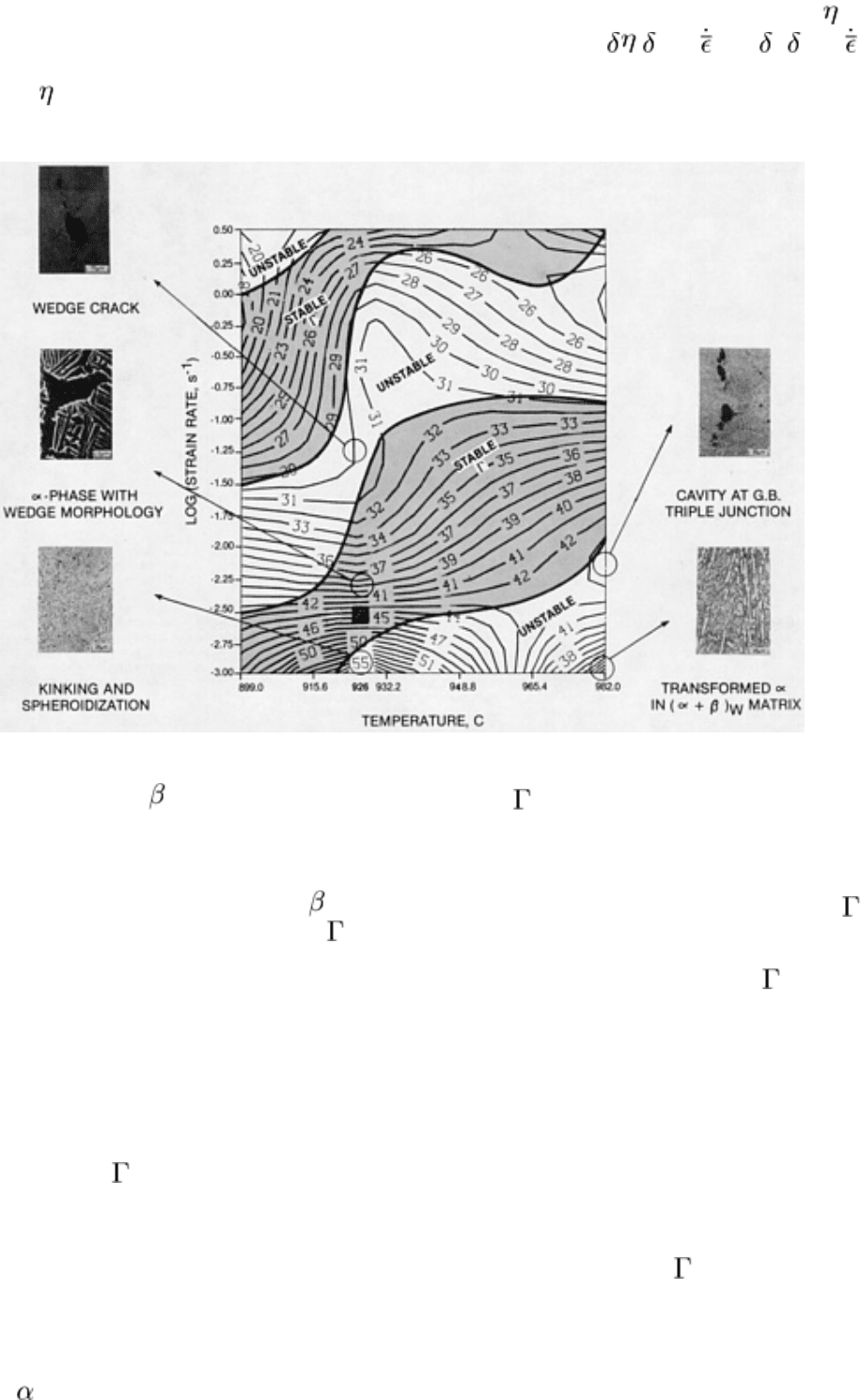
the contours of are presented as a processing map of effective strain rate versus temperature, as shown in Fig. 9.
Fig. 9 Processing map for Ti-6Al-2Sn-4Zr-2Mo alloy with stable ( ) regions and unstable regions identified
Selection of Processing Conditions
According to the processing map developed for Ti-6Al-2Sn-4Zr-2Mo (Fig. 9) using the above procedure, two (stable)
regions can be obtained in the map. There is one region in the high strain rate regime in which the efficiency is of the
order of 26% (upper left portion of Fig. 9). If hammers are to be used for forging, this processing region can be selected.
However, if a press is to be used, then it is highly recommended to select processing conditions in the region in the low
strain rate regime and high-efficiency regime (lower-central portion of Fig. 9). Parts produced by either hammer forging
or press forging have acceptable quality. This confirms the prediction that two stable regions in the Ti-6Al-2Sn-4Zr-2Mo
processing map are valid.
The next obvious question is how to determine the optimum processing conditions from the processing map in order to
obtain maximum intrinsic workability of the workpiece material. It is possible to answer this question to a certain extent
by using the efficiency values, although it is not possible to characterize the metallurgical mechanisms based on
efficiency alone. In the region, where higher efficiency is observed, it is always possible to obtain higher workability
because the rate of dissipation by the favorable stable mechanism is higher. This conclusion requires thorough
experimental and metallurgical studies that are beyond the scope of this article. However, a few microstructures are
included in the Ti-6Al-2Sn-4Zr-2Mo processing map in which peaks in the efficiency surface are observed. Peaks outside
the stable regions clearly show defects in the microstructure, while peaks inside the stable regions show an acceptable
and stable microstructure.
Another interesting point concerns the microstructure observed at 926 °C (1700 °F) and a strain rate of 5.6 × 10
-3
s
-1
.
Although observed in the stable region, this microstructure (center micrograph on the left side of Fig. 9) is not acceptable,
because the -phase formation at the grain-boundary triple junction is a potential initiation site for low-cycle fatigue

cracking. Therefore, additional microstructural studies are required for selecting optimum processing conditions for the
given application. Based on a similar argument, a temperature in the range of 899 to 920 °C (1650 to 1690 °F) and a
strain-rate of the order of 1 to 10 s
-1
are recommended if the use of hammer-forging equipment is preferred.
It is also of interest to include observations made by some forging companies. These companies have tried to forge billets
at temperatures beyond 926 °C (1700 °F) using a low strain rate of 10
-3
s
-1
. These forgings have poor properties when
compared to forgings produced below 926 °C (1700 °F) at the same strain rate. Again, this observation confirms the
prediction of unfavorable material flow under the unstable conditions of low strain rates at temperatures greater than 926
°C (1700 °F). Wedge cracks were observed in these regions.
Therefore, the successful application of Liapunov stability theory for determining optimum processing conditions for Ti-
6Al-2Sn-4Zr-2Mo demonstrates that this is a viable engineering approach for defining safe regions in processing space.
This information can then be incorporated into the finite-element code used for the simulation of metal-forming
operations.
References cited in this section
37.
H.L. Gegel, Material Behavior Modeling--An Overview, in Experimental Verification of Process Models,
Conference proceedings, C.C. Chen, Ed., American Society for Metals, 1983, p 3
38.
Y.V.R.K. Prasad,
H.L. Gegel, S.M. Doraivelu, J.C. Malas, J.T. Morgan, K.A. Lark, and D.R. Barker,
Modeling of Dynamic Material Behaviour in Hot Deformation; Forging of Ti-6242, Metall. Trans. A,
Vol
15A, 1984, p 1883
39.
H. Zeigler, Some Extremum Principles in Irreversibl
e Thermodynamics With Application to Continuum
Mechanics, in Progress in Solid Mechanics, Vol IV, John Wiley & Sons, 1963
40.
D.L. Schultz and J.L. Melsa, State Functions and Linear Control Systems, McGraw-Hill, 1967
Modeling Techniques Used in Forging Process Design
H. L. Gegel and J.C. Malas, Air Force Wright Aeronautical Laboratories/Materials Laboratory; S.M. Doraivelu and V.A. Shende,
Universal Energy Systems, Knowledge Integration Center
Analytical Process Modeling of Forging Operations
Several methods are available for the analytical modeling of the forging process. Generally, they fall into the following
categories:
• The slab method, which restricts the change of stress to only one direction
• The uniform deformation energy method, which neglects r
edundant work involved in internal shearing
due to nonuniform deformation
• The slip-line field solution, which is limited to rigid-plastic materials under plane-strain conditions
• The bounding methods, which can provide fairly good estimates of upper and l
ower limits of the
deformation force but cannot provide details of local stress and strain distributions
• The finite-element method, which provides the information required for die design and process control
All of the above approaches, except the finite-element method, are capable of providing approximate solutions to
processing problems, but are subject to some limitations. Therefore, the following discussion will consider the most
commonly used approximate methods separately from the finite-element method.
Approximate and Closed Form Solutions
In general, the boundary conditions in metal-forming operations are too complicated to be accounted for by analytical
solutions to the plasticity problem. The need to obtain at least approximate solutions has been satisfied by simplifying
assumptions, but each of the analytical approaches has its limitations. The most commonly used approximate methods
will be briefly discussed without attempting a rigorous description of the equations that are solved, because this
information is available in several other sources (Ref 41, 42, 43, 44, 45, 46, 47). These methods are described in detail
with examples in the above references and are presented in increasing order of complexity.
The Sachs (Slab) Method. In this approach, the deformation is assumed to be homogeneous, and the force
equilibrium equations are set up and solved using an appropriate yield criterion. The major deficiencies of this approach
are:
• Redundant work is not accounted for
• Stress and strain gradients are accounted for in only one direction and are assumed to be
uniform in the
perpendicular direction
The slab method is a quick way of obtaining approximate load and strain estimates in axisymmetric and plane-strain
problems and is therefore widely used.
The slip-line field approach was developed for plane-strain problems. It assumes that the material is rigid and ideally
plastic (that is, the material does not strain harden). The theory is based on the fact that any state of stress in plane strain
can be represented as the sum of a hydrostatic stress and a pure shear stress. Given the force and velocity boundary
conditions, this slip-line field is constructed. The main advantage of this method over the slab method is that it can
provide local stress calculations even when the deformation is not homogeneous. The major limitations of the slip-line
field approach are:
• It is usable only for plane-strain problems
• It assumes rigid and ideally plastic materials
• The method is tedious, and solutions are difficult to verify
The upper bound method is based on the limit theorem stating that the power dissipated by the boundary forces at
their prescribed velocities is always less than or equal to the power dissipated by the same forces under any other
kinematically acceptable velocity field. A kinematically acceptable velocity field must satisfy the velocity boundary
conditions and material incompressibility. This method allows kinematically admissible velocity fields to be set up as a
function of an unknown parameter. Power dissipation is then minimized with respect to the unknown parameter to yield a
reasonable estimate of load.
The main disadvantage of this method is that the choice of velocity field is rather arbitrary, and the poorer the selection,
the more the estimated load will exceed the true load. Another limitation is that no local stress field is compared.
The lower bound method is not of great practical significance, because forming loads are underestimated. However,
it does provide an indication of how conservative the upper bound solution is if the lower bound solution is known.
The lower bound approach is based on the limit theorem stating that the power dissipation of the actual surface forces at
their prescribed velocities is always greater than the power dissipation of the surface tractions corresponding to any other
statically admissible stress field. A statically admissible stress field must satisfy force equilibrium and not violate the
yield criterion.
Finite-Element Methods
Because of the rapid advancement of high-speed digital computer technology, numerical methods of analysis have been
developed. These include the finite-element method (FEM) and the finite-difference method (FDM). Due to the
complexity of material flow during metal forming, the finite-element method is the most suitable for analyzing such
problems. Finite-element methods, as applied to metal-forming analysis, can be classified into either elastic-plastic or
rigid-viscoplastic methods, depending on the assumptions made with regard to the material flow behavior.

The elastic-plastic method assumes that the material deformation includes a small, recoverable elastic part and a
much larger, nonrecoverable plastic part. It can give details regarding deformation loads, stresses and strains, and residual
stresses. This method has been applied to a large variety of problems, including upsetting (Ref 48), indentation (Ref 49),
extrusion (Ref 50), and expansion of a hole in a plate (Ref 51). However, because of the large change in the material flow
behavior between elastic and plastic deformation and the need to check the status of each element, the deformation steps
must be small, and this makes the method uneconomical.
The rigid-viscoplastic method assumes that the deformation stresses are primarily dependent on deformation (strain)
rates. Several programs based on the variational approach have been written by various researchers and have been applied
to the same range of problems as the elastic-plastic finite-element method (Ref 52). Although predictions regarding
residual stresses cannot be made with the rigid-viscoplastic finite-element method, the larger steps that can be used in
modeling metal-forming procedures make the method very economical, especially for modeling hot deformation.
References cited in this section
41.
T. Altan, S. Oh, and H. Gegel, Metal Forming: Fundamentals and Applications,
American Society for
Metals, 1983
42.
O. Hoffman and G. Sachs, Introduction to the Theory of Plasticity for Engineers, McGraw-Hill, 1953
43.
S. Kobayashi and E.G. Thomson, Approximate Solutions to a Problem of Press Forging, Trans. ASME,
Ser.
B, Vol 81, 1959, p 217-227
44.
B. Avitzur, Metal Forming: Processes and Analysis, McGraw-Hill, 1968
45.
W. Johnson and H. Kudo, The Mechanics of the Metal Extrusion, Manchester University Press, 1962
46.
K. Lange, Handbook of Metal Forming, McGraw-Hill, 1985
47.
R. Hill and S.J. Tupper, A New Theory of the Plastic Deformation in Wire Drawing, J. Iron Steel Inst.,
Vol
159, 1948, p 353-359
48.
C.H. Lee and S. Kobayashi, Analysis of Axisymmetrical Upsetting and Plane-Strain Side-
Pressing of Solid
Cylinders by Finite Element Method, J. Eng. Ind. (Trans. ASME), Vol 93, 1971, p 445
49.
C.H. Lee and S. Kobayashi, Elastoplastic Analysis of Plane-
Strain and Axisymmetric Flat Punch
Indentation by the Finite Element Method, Int. J. Mech. Sci., Vol 12, 1970, p 349
50.
A. Kumar, Ph.D. thesis, University of Roorkee, 1987
51.
J.S. Gunasekera and J.M. Alexander, Analysis of the Large Deformation of an Elastic-Plastic Axially-
Symmetric Continuum, in International Symposium on Foundations of Plasticity,
Noordhoff International,
1972, p 25-146
52.
S. Kobayashi, Rigid Plastic Finite-
Element Analysis of Axisymmetrical Metal Forming Processes, in
Numerical Modeling of Manufacturing Processes ASME, PVP-PB-025, 1977, p 49-68
Modeling Techniques Used in Forging Process Design
H. L. Gegel and J.C. Malas, Air Force Wright Aeronautical Laboratories/Materials Laboratory; S.M. Doraivelu and V.A. Shende,
Universal Energy Systems, Knowledge Integration Center
Analysis of Large Plastic Incremental Deformation (ALPID)
The computer program ALPID, a rigid-viscoplastic FEM program that uses the approach of Kobayashi et al., was
developed at Battelle Columbus Laboratories under the Air Force Processing Science Program (Ref 53). Important
contributions (Ref 53) to the FEM formulation included the incorporation of convenient features, such as capabilities for
handling arbitrary die geometries and remeshing. Details of this FEM formulation and some of its applications to practical
problems can be found in Ref 53. The features of ALPID are discussed below.
Finite-Element Problem Formulation in ALPID. The Cartesian coordinate is used to derive the minimum
principle. Generalization of this formulation to other coordinate systems can be made without difficulty. With regard to
Eq 47, 48, 49, 50, 51, 52, 53, 54, and 55, a body of volume, V, is considered with the traction, F, prescribed on a part of
the surface, S
F
, and the velocity, V, prescribed on the remainder of the surface, S
U
. The body is composed of a rigid-plastic
material that obeys the von Mises yield criterion and its associated flow rule. Body forces are assumed to be absent. The
actual stress,
ij
, and velocity field, v, satisfy the following relations.
Equilibrium conditions, neglecting body forces, are:
ij, j
= 0
(Eq 47)
where
ij
is the stress tensor and
,j
denotes partial differentiation with respect to j.
The compatibility condition is given by:
ij
= (V
i,j
+ V
j,i
)
(Eq 48)
where
ij
and V
i
are the strain rate and velocity, respectively.
The constitutive relations are given in Eq 49, 50, and 51:
(Eq 49)
where '
ij
is the deviatoric component of the stress tensor:
(Eq 50)
and
(Eq 51)
Equations 49, 50, and 51 are valid for fully dense ingot metallurgy alloys. For powder metallurgy alloys, Eq 49, 50, and
51 must be modified to include hydrostatic stress, as shown in a later section in this article. The flow stress is generally a
function of total strain, strain rate, temperature, relative density, and microstructure.
The boundary conditions are given by:
ij
n
i
= F
j
on S
F
(Eq 52)
and
v
i
= V
i
on S
U
(Eq 53)
and |fs| is the frictional stress with the proper sign, where n
i
is the unit vector normal to the surface.
Equations 51, 52, and 53 can be put into the variational principle as:
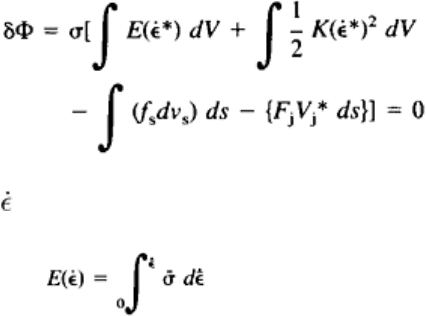
(Eq 54)
where the work function E( ) can be expressed as:
(Eq 55)
In Eq 54, K is a large positive constant that penalizes the dilational strain, and * denotes the restriction of the velocity
fields to the trial space. The standard procedure of discretionization of this function can be found in Ref 54.
Computational Scheme of ALPID. The processing phase of ALPID has two major stages. The first is the guess
generation stage, which generates an initial solution (guess) assuming a linear material relationship. The second is the
solution stage for the actual nonlinear constitutive behavior of the material. These stages will be briefly discussed; Fig. 10
shows a simplified flow chart that outlines the operation of ALPID.
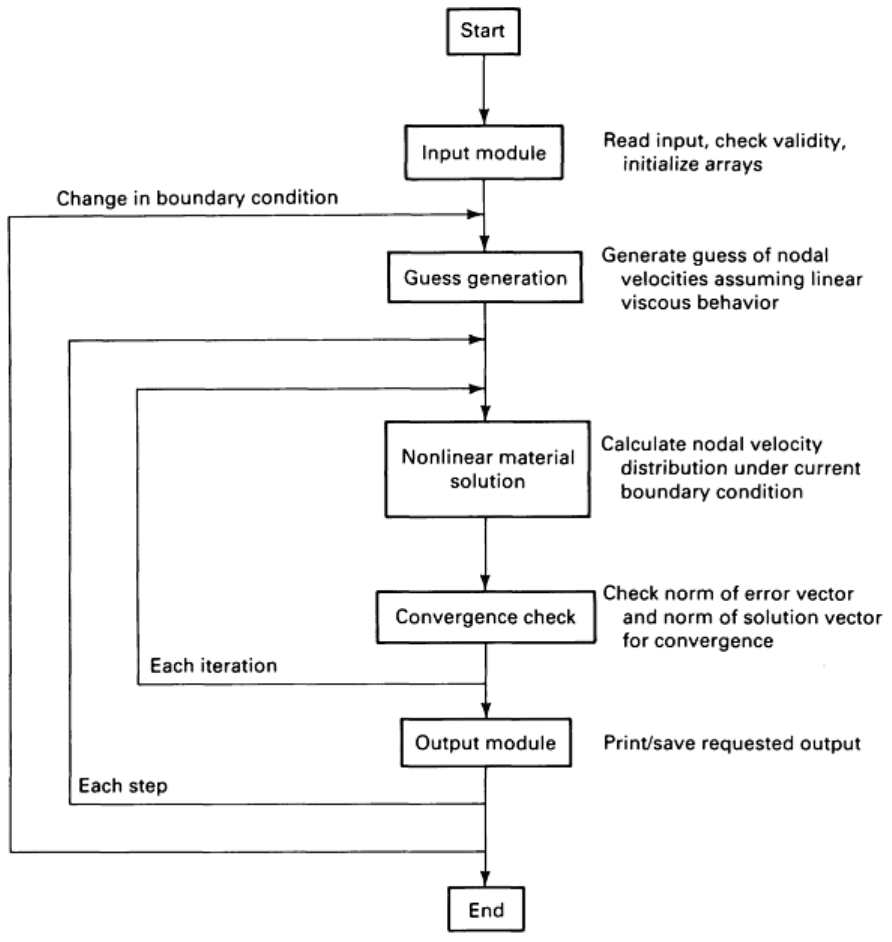
Fig. 10 Simplified flow chart showing steps in the operation of ALPID
Guess generation provides a good guess of the velocities at the nodal points in the finite-element mesh. Because
ALPID uses the Newton-Raphson method to solve the nonlinear system of equations, it is important to have a good initial
guess. This initial guess is necessary when previous solutions are not available or not applicable. A guess of the velocity
distribution is also required each time the boundary conditions change. Boundary conditions change whenever a node
comes into contact with a die or whenever a node in contact with a die becomes a free node. The steps in guess generation
are:
• Generation of the element stiffness matrix assuming linear behavior of the materials
• Application of displacement boundary conditions
• Addition of element stiffness matrices to the global stiffness matrix
• Application of force boundary condition
• Solution of resulting linear equations
Solution Stage for Nonlinear Materials. The guesses of velocities generated in the previous stage of execution are
used to estimate the material properties and to identify rigid and viscoplastic elements. This information is used to
generate the element stiffness matrix. The steps involved in the solution for nonlinear materials are:
• Obtain yield stress of the elements to identify the rigid element
• Generate element stiffness matrix using
1. linear behavior for rigid elements and
2. actual constitutive behavior for viscoplastic elements
• Apply shear friction boundary condition, if applicable
• Add to the global stiffness matrix
• Apply Coulomb friction boundary condition, if applicable
• Determine iteration strategy and step length
• Solve a system of linear equations
• Check for convergence
This process is repeated until convergence is obtained. Execution stops if the solution does not converge in a specified
number of attempts. When convergence is obtained, the nodal coordinates are updated, and all of the post calculations are
completed. If there is no change in the boundary conditions, the solution from each step is used as the initial guess for the
next step.
The stiffness matrix generation involves the following steps:
• Obtain the shape function and shape function derivatives at the Gauss integration points of an element
• Change from natural to global coordinates to obtain the [B] matrix
• Obtain the strain rate hardening parameter
• Calculate [B]
T
[D] [B] matrix at each integration point and multiply by weighting factor
• Repeat for each integration point to obtain the stiffness matrix of each element
• Impose volume constancy constraint on stiffness matrix
Versions of ALPID. Many versions of ALPID are available. ALPID 1.0 was validated for solving two-dimensional (2-
D) plane-strain and axisymmetric problems related to metal forming under isothermal processing conditions. In ALPID
2.0, the rigid-viscoplastic formulation is coupled with a heat-transfer module to solve these problems under hot-working
conditions (Ref 55). A new yield function was developed to enable the analysis of compressible materials (Ref 6). Based
on these criteria and on plasticity theory developed for porous materials, ALPID 1.4 was developed to solve 2-D plane-
strain and axisymmetric problems related to P/M metal-forming operations under isothermal processing conditions (Ref
56).
ALPID-3D was also developed and validated to solve problems involving complex material flow in three directions (Ref
57). These finite-element programs are being used for simulating such metal-forming operations as forging, extrusion,
and rolling and for predicting lap or folding formation in rib-web forging, center burst formation in extrusion, and the
occurrence of plastic instability (such as adiabatic shearing) in rolling. Some industries are using these tools for press
selection, for optimizing process and die design, and for ensuring die filling in 2-D axisymmetric and plane-strain
problems.
Attempts at developing process control algorithms have been successful (Ref 58). Optimal design procedures have been
introduced as nonholonomic constraints for the development of control algorithms to ensure that, during spike forging,
the control elements keep the deforming material within the allowable temperature and strain rate range as specified by
the dynamic material modeling approach. Therefore, the technical feasibility of using analytical techniques to solve
process design and control problems in metal forging has been established.
