ASM Metals HandBook Vol. 14 - Forming and Forging

Подождите немного. Документ загружается.

the mesh, the lower of the

values is accepted as the actual stress. Thus, a tentlike stress distribution is obtained (Fig.

9). Integration of the stresses acting on the plane of contact gives the roll-separating force.

Fig. 8

Stress analysis of the rolling of plates. (a) Top view of the rolled plate. (b) Stresses in the rolling

direction. (c) Stresses in the transverse direction. Source: Ref 16

Fig. 9 The calculated stress (

) distribution in plate rolling shown three-dimensionally. Source: Ref 16.

References cited in this section

16.

G.D. Lahoti, et al., Computer Aided Analysis of Metal Flow and Stresses in Plate Rolling, J. Mech.

Work.

Technol., Vol 4, 1980, p 105

19.

S. Ekelund, in Roll Pass Design, VEB Deutscher Verlag, 1963, p 48 (in German)

20.

Z. Wusatowski, Hot Rolling: A Study of Draught, Spread and Elongation, Iron Steel, Vol 28, 1955, p 69

21.

L.G.M. Sparling, Formula for Spread in Hot Rolling, in

Proceedings of the Institute of Mechanical

Engineers, Vol 175, 1961, p 604

22.

S.-I. Oh and S. Kobayashi, An Approximate Method for Three-Dimensional Analysis of Rolling, Int.

Mech. Sci., Vol 17, 1975, p 293

23.

R. Kummerling and H. Lipmann, On Spread on Rolling, Mech. Res. Commun., Vol 2, 1975, p 113

24.

H. Neumann, Design of Rolls in Shape Rolling, VEB Deutscher Verlag, 1969 (in German)

25.

R. Hill, A General Method of Analysis for Metalworking Processes, Inst. J. Mech. Sci., Vol 16, 1974, p 521

Flat, Bar, and Shape Rolling

G. D. Lahoti, The Timken Company; S.L. Semiatin, Battelle Columbus Division

Shape Rolling

Rolling of shapes, also called caliber rolling, is one of the most complex deformation processes. A round or round-

cornered square bar, billet, or slab is rolled in several passes into relatively simple sections such as rounds, squares, or

rectangles; or complex sections such as L, U, T, H, or other irregular shapes (Ref 26). For this purpose certain

intermediate shapes or passes are used, as shown in Fig. 10 for the rolling of angle sections (Ref 27). The design of these

intermediate shapes, that is, roll pass design, is based on experience and differs from one company to another, even for

the same final rolled section geometry. Relatively few quantitative data on roll pass design are available in the literature.

Good summaries of references on this subject are given in several books (Ref 24, 26, 28, 29, 30, 31) and in a few recent

articles (Ref 32, 33).

Fig. 10 Five possible roll pass designs for the rolling of a steel angle section. Source: Ref 27.

Basically, there are two methods for rolling shapes or sections. The first method is universal rolling (Fig. 11). The second

method is caliber rolling (Fig. 10, 12). In universal rolling, the mill and stand constructions are more complex. However,

in the rolling of I-beams or other similar sections, this method allows more flexibility than does caliber rolling and

requires fewer passes. This is achieved because this method provides appropriate amounts of reductions, separately in

webs and flanges.

Fig. 11 Universal rolling of flanged beams. (a) Universal roll stand. (b) Edging stand. (c) Finishi

ng stand.

Source: Ref 34

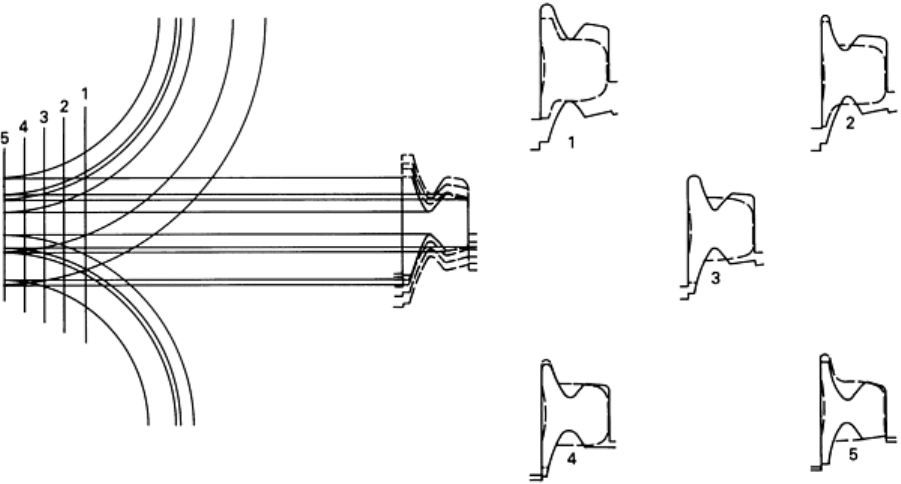
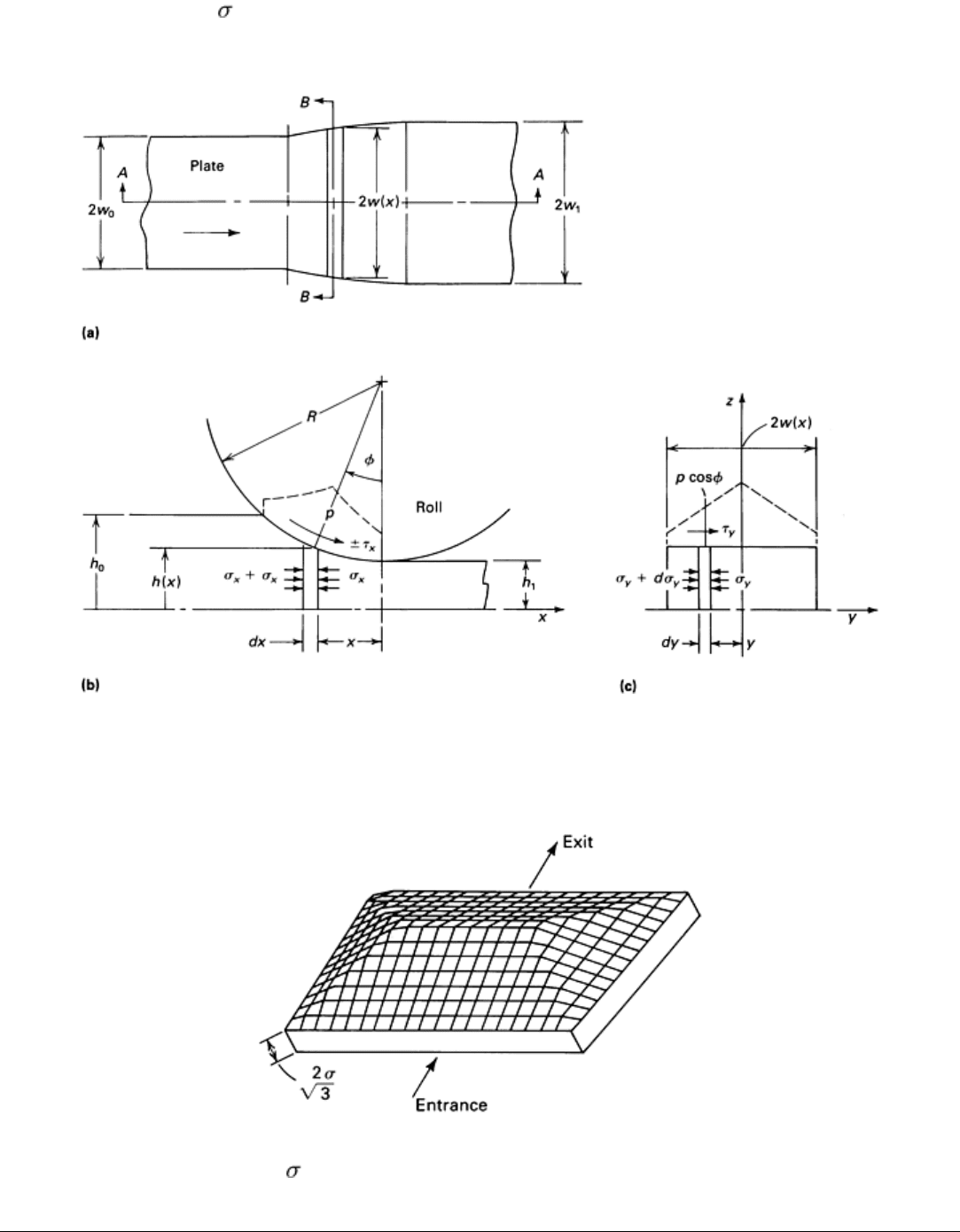
Fig. 12

Analysis of a roll stand used in rolling of rails. Sketches 1 through 5 illustrate the stock in broken lines

and the roll in solid lines at various positions in the deformation zone. Source: Ref 35

For successful rolling of shapes, it is necessary to estimate for each stand: the roll separating force and torque, the spread

and elongation, and the appropriate geometry of the roll cavity or caliber. The force and torque can be estimated either by

using empirical formulas or by approximating the deformation in shape rolling with that occurring in an "equivalent"

plate rolling operation. In this case, the "equivalent" plate has initial and final thicknesses that correspond to the average

initial and final thicknesses of the rolled section. The load and torque calculations can be performed for the "equivalent"

plate, as discussed earlier in this chapter for plate rolling. The results are approximately valid for the rolled shape being

considered.

Estimation of Elongation. During the rolling of a given shape or section, the cross section is not deformed uniformly,

as can easily be seen in Fig. 12. This is illustrated further in Fig. 13 for a relatively simple shape. The reductions in height

for zones A and B are not equal (Fig. 13a). Consequently, if these two zones, A and B, were completely independent of

each other (Fig. 13b), zone B would be much more elongated than zone A. However, the two zones are connected and, as

part of the rolled shape, must have equal elongation at the exit from the rolls. Therefore, during rolling, metal must flow

from zone B into zone A so that a uniform elongation of the overall cross section is obtained (Fig. 13c). This lateral flow

is influenced by the temperature differences that exist in the cross section because of variations in material thickness and

heat flow.

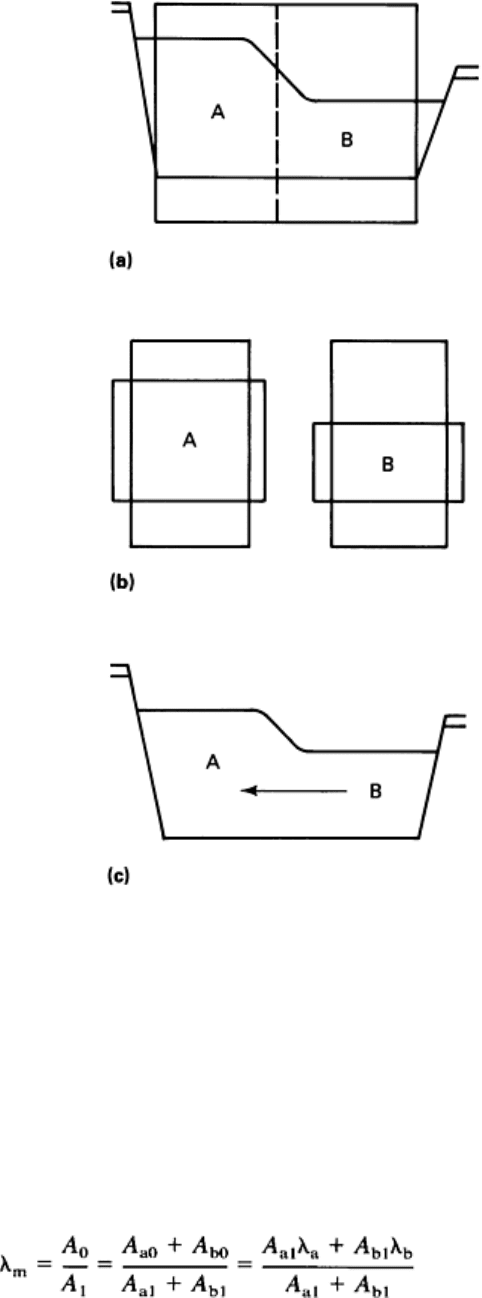
Fig. 13

Nonuniform deformation in the rolling of a shape. (a) Initial and final sections. (b) Two zones of the

section considered as separate plates. (c) Direction of lateral metal flow. Source: Ref 24

To estimate the overall elongation, it is necessary to divide the initial section into a number of "equivalent" plates (A, B,

C, and so forth), as shown in Fig. 13. The elongation for an individual section, without the combined influence of other

portions of the section, can be estimated by using both the plate-rolling analogy and the techniques discussed in this

article. The combined effect can be calculated by taking a "weighted average" of the individual elongations. For example,

if the original section is to be divided into an equivalent system consisting or two plate sections (A and B in Fig. 13), with

individual cross-sectional areas A

and A

, then the following weighted-average formula can be used:

(Eq 21)

where λ is the elongation coefficient (that is, the cross-sectional area at the entrance divided by the cross-sectional area at

the exit); A is the cross-sectional area; m is a subscript denoting average; a and b are subscripts denoting section portions

A and B; and 0 and 1 are subscripts denoting entrance and exit values, respectively.

Computer-Aided Roll Pass Design. Estimation of the number of passes and of the roll geometry for each pass is the

most difficult aspect of shape rolling. Ideally, to accomplish this, certain factors, discussed below, must be considered.

The Characteristics of the Available Installation. These include diameters and lengths of the rolls, bar

dimensions, distance between roll stands, distance from the last stand to the shear, and tolerances that are required and

that can be maintained.

The reduction per pass must be adjusted so that the installation is used at a maximum capacity, the roll stands are not

overloaded, and roll wear is minimized. The maximum value of the reduction per pass is limited by the excessive lateral

metal flow, which results in edge cracking; the power and load capacity of the roll stand; the requirement for the rolls to

bite in the incoming bar; roll wear; and tolerance requirements.

At the present stage of technology, the above factors are considered in roll pass design by using a combination of

empirical knowledge, some calculations, and some educated guesses. A methodical way of designing roll passes requires

not only an estimate of the average elongation, as discussed earlier, but also the variation of this elongation within the

deformation zone. The deformation zone is limited by the entrance, where a prerolled shape enters the rolls, and by the

exit, where the rolled shape leaves the rolls. This is illustrated in Fig. 12. The deformation zone is cross sectioned with

several planes (for example, planes 1 to 5 in Fig. 12; 1 is at the entrance, 5 is at the exit). The roll position and the

deformation of the incoming billet are investigated at each of these planes. Thus, a more detailed analysis of metal flow

and an improved method for designing the configuration of the rolls are possible. It is evident that this process can be

drastically improved and made extremely efficient by the use of computer-aided techniques.

In recent years, most companies that produce shapes have computerized their roll pass design procedures for rolling

rounds (Ref 33, 36, 37, 38, 39, 40) or structural shapes (Ref 36, 40, 41, 42, 43). In most of these applications, the

elongation per pass and the distribution of the elongation within the deformation zone for each pass are predicted by using

an empirical formula. If the elongation per pass is known, it is then possible, by use of computer graphics, to calculate the

cross-sectional area of a section for a given pass, that is, the reduction and the roll geometry. The roll geometry can be

expressed parametrically (in terms of angles, radii, and so forth). These geometric parameters can then be varied to

optimize the area reduction per pass and obtain an acceptable degree of fill of the roll caliber used for that pass.

Computer-Aided Roll Pass Design of Airfoil Sections. To analyze metal flow and predict force and torque in the

rolling of airfoils, two computer programs have been developed in a recent study (Ref 17). The first of these programs,

SHPROL, uses upper bound analysis in a numerical form to predict spread and roll torque. SHPROL is based on the

following simplifying assumptions:

•

The initial contact between the rolls and the entrance section can be approximated as a straight line.

(This is only correct if the upper and lower surfaces of the initial section already have the shape of the

rolls.)

• An airfoil shape can be considered as an aggregate of slabs, as shown in Fig. 14.

• Plane sections perpendicular to the r

olling direction remain plane during rolling. Thus, the axial velocity

(velocity in the rolling, or x,

direction) at any section perpendicular to the rolling direction is uniform

over the entire cross section.

• The velocity components in the transverse, or y, direction and in the thickness, or z,

direction are

functions of x and linear in the y and z coordinates, respectively.

Fig. 14 Configuration of deformation zone in the application of numerical upper-

bound analysis to the rolling of

airfoil shapes. Source: Ref 17

In Fig. 14 each element is considered to be a plate for which it is possible to derive a kinematically admissible velocity

field. The total energy dissipation rate of the process

is:

(Eq 22)

where

is the energy rate of plastic deformation, and is calculated for each element by integrating the product of flow

stress and the strain rate over the element volume;

represents the energy rates associated with velocity discontinuities

and is due to internal shear between the elements; and

is the energy rate due to friction between the rolls and the

deforming material.

The total energy dissipation rate

is a function of unknown spread profiles w

and w

(Fig. 14) and the location of the

neutral plane x

. As in the analysis discussed earlier for plate rolling, the unknown coefficients of w

, w

, and x

are

determined by minimizing the total energy rate.

The computer program SHPROL uses as input data: roll and incoming-shape geometry, friction, flow stress, and roll

speed. SHPROL can predict the energy dissipation rates, the roll torque, and, most important, the amounts of elongation

and spread within one deformation zone, in the rolling of any airfoil shape.

The second program, called ROLPAS, uses interactive graphics and is capable of simulating the metal flow in the rolling

of relatively simple shapes, such as rounds, plates, ovals, and airfoils (Fig. 15). ROLPAS uses as input: the geometry of

the initial section, the geometry of the final section, the flow stress of the rolled material and the friction factor, and the

variations in elongation and spread in the rolling direction, as calculated by the SHPROL program.

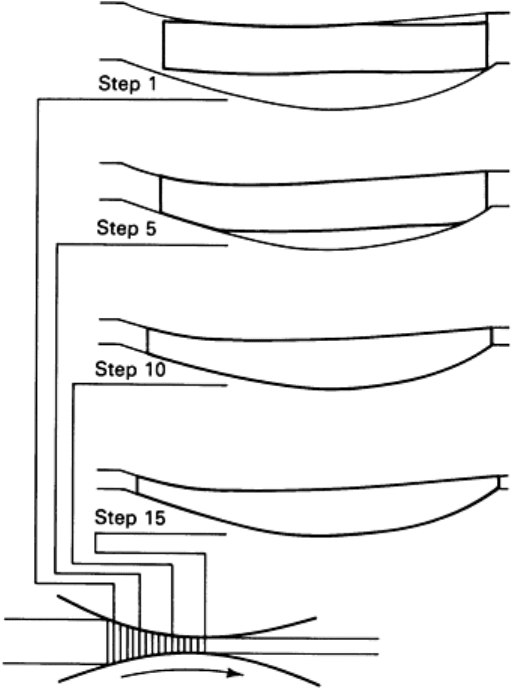
Fig. 15 Selected simulation steps as displayed by ROLPAS for a test airfoil shape cold

rolled from rectangular

steel stock

To simulate the rolling process, ROLPAS divides the deformation zone into a number of cross sections parallel to the roll

axis (Fig. 7, 15). The simulation is initiated by considering the cross-sectional area, stresses present, and the roll-

separating force and torque for the first section. These same analyses can then be performed on any succeeding section.

Computer-Aided Roll Pass Design for Round Sections. Several computer-aided methods for designing caliber

rolls for rod rolling have been discussed in the literature (Ref 33, 36, 37, 38, 39, 40). One of these methods is a computer

program called RPDROD for establishing roll cross sections and pass schedules interacting with a graphics terminal (Ref

33). RPDROD uses an empirical formula for estimating the variation of the spread in the roll bite and parametrically

described alternative roll caliber designs. When using this program, the designer obtains an optimum roll pass schedule by

evaluating a number of alternatives in which individual pass designs are selected from a variety of caliber shapes

commonly used in rod rolling.

The computer program RPDROD consists of four modules, called STOCK, SCHEDULE, GROOVE, and METAL

FLOW. The STOCK design module allows the user to design/specify the entry cross section for the first pass in the

schedule. A square, rectangular, or round stock cross section can be defined. The SCHEDULE design module allows the

user to design the roll pass schedule by providing specific functions:

• Add a new pass to the roll pass schedule, by es

timating alternative roll cross section dimensions from

design data provided by spread/elongation calculations

• Delete pass design data from the schedule in order to investigate alternative pass designs

• Review and/or provide hard copy of existing pass design data

The SCHEDULE design module allows the user to design an optimum roll pass schedule by investigating various

alternative pass design and/or shape combinations. In principle, any roll cross section shape considered by the program

could be used for a given pass in the schedule. However, RPDROD has facilities for checking input data and thus for

preventing the selection of an illogical pass design or the inappropriate selection of roll cross-sectional shape

combinations.

The GROOVE design module can be used to change the initially suggested roll cross section dimensions, as the user

deems appropriate. As in the SCHEDULE module, input checking facilities ensure that specified roll cross-sectional

dimensions are consistent with the chosen roll cross-sectional shape and bar entry cross section.

The METAL FLOW design module provides the user with details of metal flow simulation, including the calculated cross

sections of the deforming bar in the roll bite, stresses in the deforming material, roll separating load, and roll torque. For

this purpose, this module uses the ROLPAS program discussed earlier for the rolling of airfoil shapes.

As an example, a pass schedule calculated with RPDROD is given in Table 1. Comparison of these results with laboratory

experiments indicated that these predictions were reasonably accurate, and RPDROD can be used for practical roll pass

design for rolling of round sections (Ref 33).

Table 1 Summary of pass schedule information for the laboratory experiments as simulated by RPDROD

Pass

number

Groove

shape

Rotation

angle,

degrees

Exit

area,

in.

Exit

speed,

ft/min

Reduction

in area, %

Area

fill,

Roll

force,

tonf

Horse-

power

Roll

speed,

rpm

Stock Square 0.0 1.559

60.0

1 Square 45.0 1.394

55.6 10.6 93.2 5.3 1.3

30.0

2 Square 90.0 1.171

57.5 16.0 96.1 16.3 6.3

30.0

3 Square 90.0 1.042

57.7 11.0 95.7 8.7 2.5

30.0

4 Oval 45.0 0.873

59.4 16.2 98.8 14.1 6.2

30.0

5 Round 90.0 0.780

58.1 10.6 99.3 5.9 1.9

30.0

6 Oval 90.0 0.675

58.3 13.5 101.1

9.1 2.9

30.0

7 Round 90.0 0.595

59.1 11.8 98.9 4.8 1.4 30.0

Computer-Aided Roll Pass Design of Structural and Irregular Sections. Computer graphics is being used by

many companies for the design and manufacture of the caliber shapes for the rolling of structural sections (Ref 36, 40, 41,

42, 43). A publication on this subject gives an excellent summary of the practical use of computer graphics for roll caliber

and roll pass design (Ref 43). In this case, the cross section of a rolled shape is described in general form as a polygon.

Each corner or fillet point of the polygon is identified with the x and y coordinates and with the value of the

corresponding radius (Fig. 16). Thus, any rolled section can be represented by a sequence of lines and circles. This

method of describing a rolled section is very general and can define a large number of sections with a single computer

program. Lines or circles that are irrelevant in a specific case can be set equal to zero. Thus, a simpler section, with a

smaller number of corner and fillet points, can be obtained. For example, in the rolling of the symmetric-angle section

shown in Fig. 10, several intermediate section passes are required. Such an intermediate section is shown in parametric

representation in Fig. 17. In this figure, all the geometric variables can be modified to change the cross-sectional area

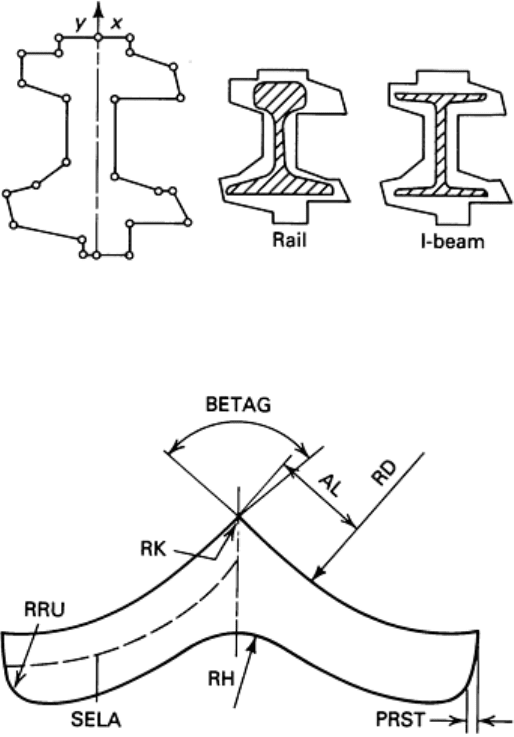
and/or the amount of reduction per pass. These variables, which fully describe this section, are SELA = length (of one

leg) at centerline, BETAG = angle at top corner, RK = radius at top corner, AL = length of straight portion at top, RD =

radius of leg at top, PRST = projection of draft angle, RRU = radius at lower tip of leg, and RH = radius at bottom corner.

Fig. 16 Geometric representation of a rolled section as a polygon. Source: Ref 43

Fig. 17 Parametric representation of an intermediate-shape rolling pass for a symmetric angle section.