ASM Metals HandBook Vol. 14 - Forming and Forging
Подождите немного. Документ загружается.

Some materials that are difficult or impossible to forge cold can be successfully formed at higher temperature, thus
expanding the range of materials used in cold forging. Many materials must be annealed prior to cold forging. For
example, for medium-carbon to high-carbon steels, a long spheroidize anneal may be necessary. In parts requiring
extensive deformation, one or more intermediate anneals may be necessary to counteract the effect of work hardening.
Increasing the forging temperature can eliminate the need for these relatively costly and energy-intensive anneals. Within
limits determined by the metallurgical response of the workpiece material, the process temperature can be adjusted so that
the strength level in the forging is at the desired level. This can help to eliminate the need for heat treatment after forging.
Some geometries that may be difficult to forge cold can be readily accomplished with increased forging temperature. For
example, for a given material, thinner flanges and sharper corners and shoulders could usually be produced at increased
temperatures. A given material can generally accommodate greater deformation before cracking when forged at higher
temperature, and a given geometry can sometimes be forged in fewer stations in comparison with cold forging.
Selection of the process temperature will be based first on the workpiece characteristics to ensure that the metal flow
stress is low enough to allow forging on available equipment and that workability is sufficient to allow the required
deformation without cracking. Unfortunately, in comparison with what is needed, the literature contains limited data on
material flow stress and workability as a function of temperature.
At relatively low temperatures, flow stress is primarily a function of strain. At higher temperatures, strain is less important
than strain rate. At intermediate (warm) temperatures, both strain and strain rate may be important. Flow stress data can
be presented in either graphical or tabular form. In the case of the latter, values of coefficients for a constitutive equation
are tabulated.
Both strain dependent and strain-rate dependent coefficients have been obtained for numerous materials by utilizing the
least-mean-square-fit technique to calculate the coefficients from stress-strain curves. An empirical expression for the
strain dependency of the flow stress, , is:
= K( )
n
(Eq 2)
where is the true or logarithmic strain, and K and n are empirical constants. Strain dependent data for carbon steels are
shown in Table 1 and data for alloy steels in Table 2.
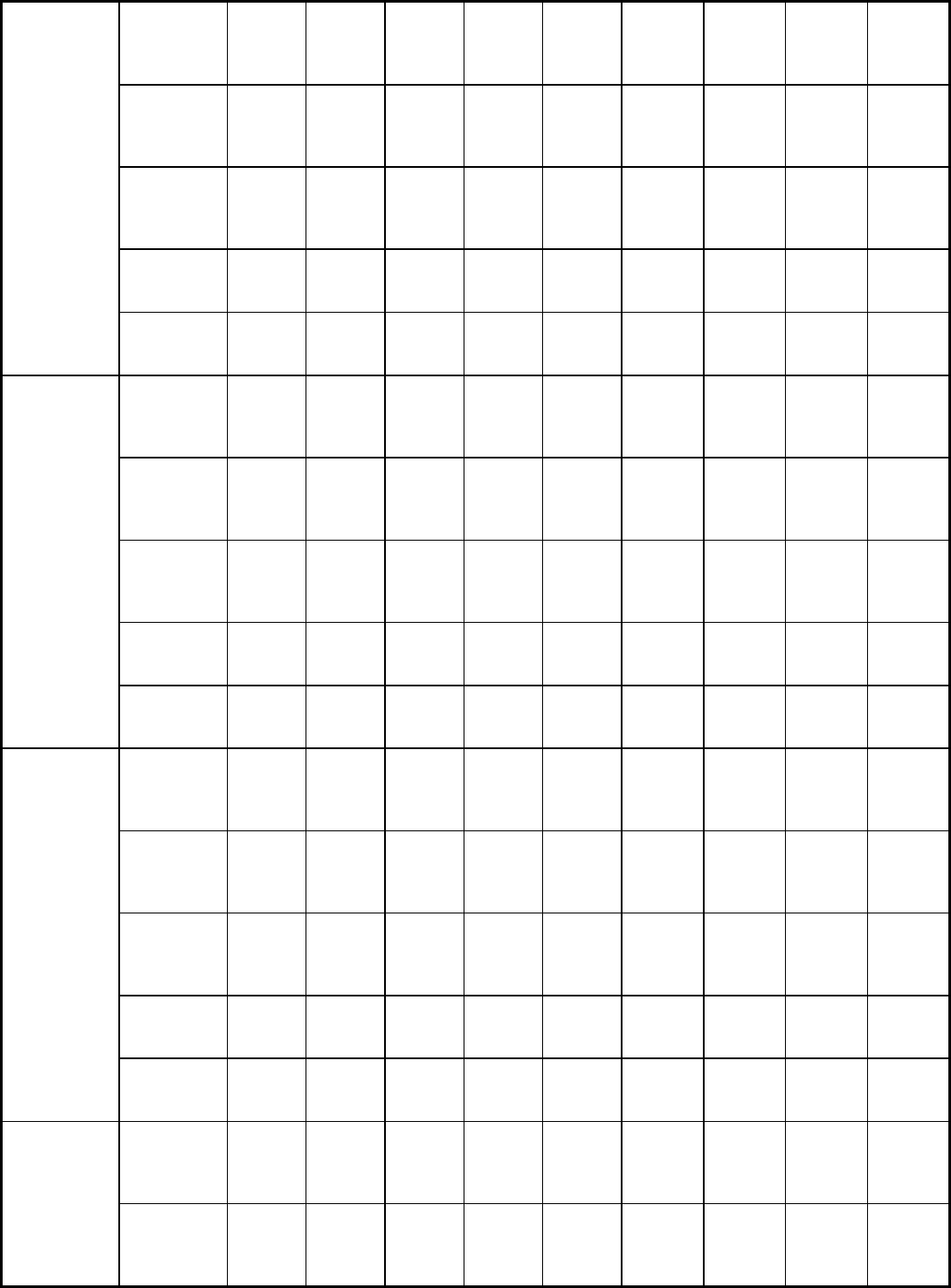
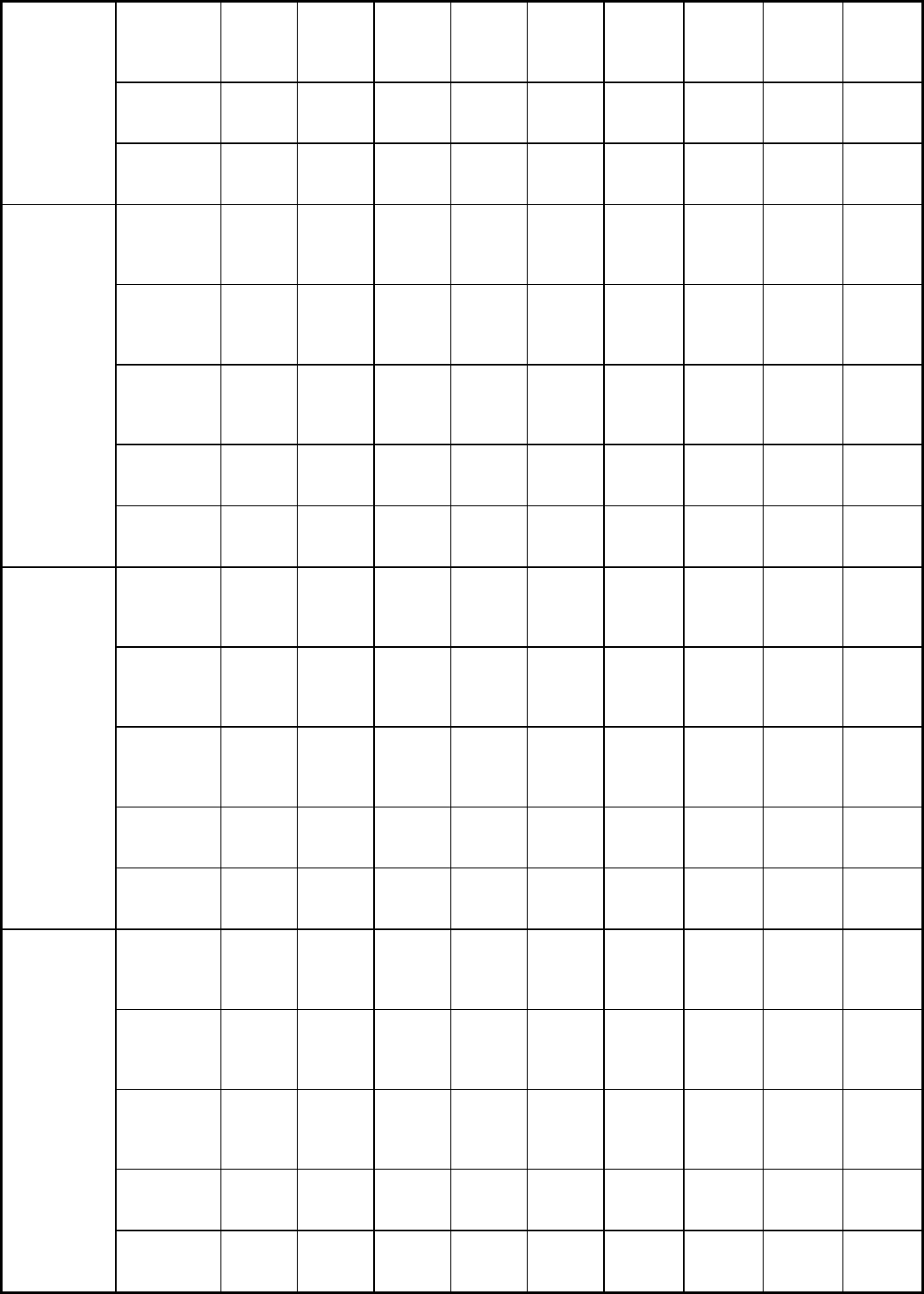
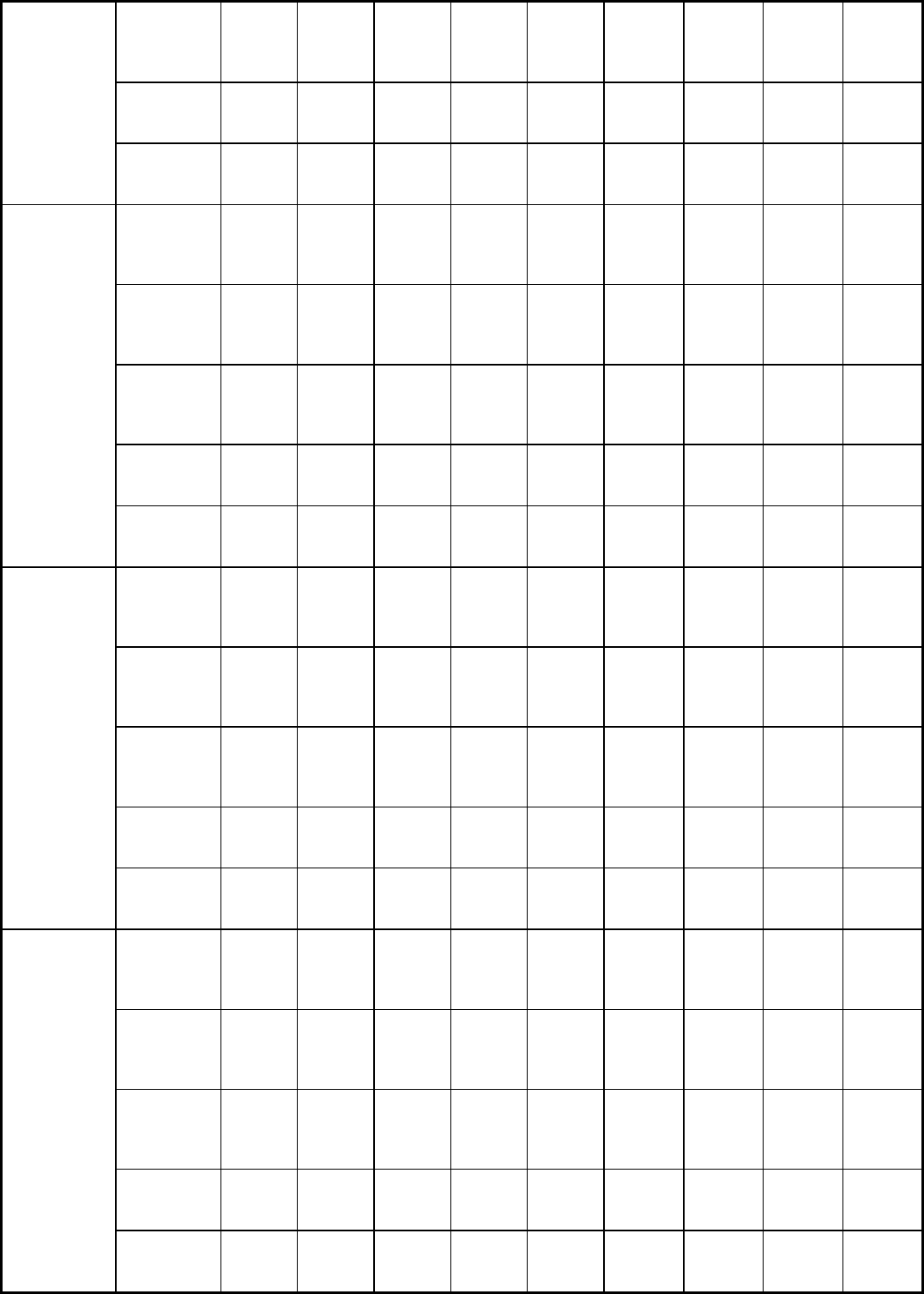
Table 1 Mechanical properties of carbon steels
Average strain rate: 8 mm/mm/s (8 in./in./s). Source: Ref 2
Testing temperature °C (°F)
Steel grade
and
condition
(a)
Property
(b)
25 (75) 205
(400)
400
(750)
455
(850)
510
(950)
565
(1050)
620
(1150)
675
(1250)
815
(1500)
K
f
, MPa
(ksi)
. . . 525 (76)
615 (89)
660 (96)
615 (89)
505 (73) 400 (58) 295 (43)
172 (25)
TS, MPa
(ksi)
370 (54)
275 (40)
310 (45)
340 (49)
330 (48)
290 (42) 250 (36) 205 (30)
110 (16)
YS, MPa
(ksi)
. . . 90 (13) 95 (14) 115 (17)
115 (17)
140 (20) 140 (20) 145 (21)
55 (8.2)
RA, % 80 80 72 70 77 87 93 97
98
1005 HR
n
. . . 0.28 0.30 0.28 0.26 0.21 0.17 0.12
0.18
K
f
, MPa
(ksi)
950
(138)
740
(107)
915
(133)
945
(137)
820
(119)
650 (94) 525 (76) 395 (57)
360 (52)
TS, MPa
(ksi)
520 (75)
405 (59)
500 (71)
510 (74)
460 (67)
415 (60) 340 (49) 260 (38)
180 (26)
YS, MPa
(ksi)
200 (29)
160 (23)
185 (27)
200 (29)
195 (28)
215 (31) 200 (29) 170 (25)
45 (6.9)
RA, % 65 68 49 57 76 87 93 96
95
1018 HR
n
0.25 0.25 0.26 0.25 0.23 0.18 0.15 0.13
0.32
K
f
, MPa
(ksi)
905
(131)
. . . . . . . . . . . . . . . 475 (69) 370 (54)
330 (48)
TS, MPa
(ksi)
495 (72)
. . . . . . . . . . . . . . . 305 (44) 240 (35)
170 (25)
YS, MPa
(ksi)
195 (28)
. . . . . . . . . . . . . . . 180 (26) 180 (26)
60 (8.4)
RA, % 63 . . . . . . . . . . . . . . . 89 92
94
1023 HR
n
0.25 . . . . . . . . . . . . . . . 0.16 0.12
0.28
K
f
, MPa
(ksi)
1220
(177)
945
(137)
1015
(147)
1035
(150)
950
(138)
805
(117)
605 (88) 455 (66)
345 (50)
TS, MPa
(ksi)
690
(100)
545 (79)
595 (86)
595 (86)
595 (82)
505 (73) 400 (58) 317 (46)
190 (27)
YS, MPa
(ksi)
305 (44)
255 (37)
290 (42)
270 (39)
285 (41)
285 (41) 260 (38) 215 (31)
70 (10)
RA, % 53 56 42 47 68 80 81 88
97
1040 HR
n
0.23 0.21 0.20 0.22 0.19 0.17 0.14 0.12
0.26
K
f
, MPa
(ksi)
1400
(203)
1110
(161)
1140
(165)
1220
(177)
1075
(156)
860
(125)
725
(105)
545 (79)
360 (52)
1045 HR
TS, MPa
(ksi)
785
(114)
660 (96)
675 (98)
705
(102)
640 (93)
565 (82) 470 (68) 360 (52)
200 (29)
YS, MPa
(ksi)
350 (51)
315 (46)
345 (50)
325 (47)
330 (48)
325 (47) 260 (38) 235 (34)
75 (11)
RA, % 47 48 33 37 52 57 60 76
95
n
0.22 0.20 0.19 0.22 0.19 0.19 0.18 0.14
0.26
K
f
, MPa
(ksi)
2180
(316)
1650
(239)
1605
(233)
1570
(228)
1450
(210)
1185
(172)
1140
(165)
940
(136)
360 (52)
TS, MPa
(ksi)
1035
(150)
850
(123)
860
(125)
915
(133)
840
(122)
705
(102)
600 (87) 460 (67)
195 (28)
YS, MPa
(ksi)
435 (63)
420 (61)
495 (72)
545 (79)
505 (73)
440 (64) 330 (48) 215 (31)
95 (14)
RA, % 24 31 18 18 25 23 28 30
98
1080 HR
n
0.26 0.22 0.19 0.17 . . . 0.16 0.20 0.24
0.21
K
f
, MPa
(ksi)
910
(132)
. . . . . . . . . . . . . . . 470 (68) 360 (52)
360 (52)
TS, MPa
(ksi)
485 (70)
. . . . . . . . . . . . . . . 295 (43) 240 (35)
170 (25)
YS, MPa
(ksi)
165 (24)
. . . . . . . . . . . . . . . 180 (26) 165 (24)
50 (5.9)
RA, % 68 . . . . . . . . . . . . . . . 89 94
90
1117 N
n
0.27 . . . . . . . . . . . . . . . 0.15 0.12
0.35
K
f
, MPa
(ksi)
1325
(192)
1040
(151)
1055
(153)
1165
(169)
1010
(146)
880
(128)
655 (95) 540 (78)
360 (52)
TS, MPa
(ksi)
765
(111)
625 (91)
635 (92)
675 (98)
625 (91)
545 (79) 435 (63) 330 (48)
190 (27)
YS, MPa
(ksi)
365 (53)
325 (47)
330 (48)
315 (46)
350 (51)
345 (50) 275 (40) 200 (29)
65 (9.2)
RA, % 53 53 41 44 63 78 85 91
94
1137 HR
n
0.21 0.19 0.19 0.21 0.17 0.16 0.15 0.16
0.20

K
f
, MPa
(ksi)
820
(119)
. . . . . . . . . . . . 585 (85) 435 (63) . . .
220 (32)
TS, MPa
(ksi)
455 (66)
. . . . . . . . . . . . 360 (52) 295 (43) 235 (34)
130 (19)
YS, MPa
(ksi)
185 (27)
. . . . . . . . . . . . 185 (27) 195 (28) . . .
65 (9.4)
RA, % 59 . . . . . . . . . . . . 69 79 87
87
1213 N
n
0.24 . . . . . . . . . . . . 0.18 0.13 . . .
0.20
K
f
, MPa
(ksi)
1130
(124)
745
(108)
940
(136)
960
(139)
815
(118)
635 (92) 490 (71) 360 (52)
230 (33)
TS, MPa
(ksi)
460 (67)
395 (57)
475 (69)
485 (70)
435 (63)
370 (54) 310 (45) 250 (36)
140 (20)
YS, MPa
(ksi)
165 (24)
140 (20)
160 (23)
150 (22)
160 (23)
185 (27) 185 (27) 180 (26)
75 (11)
RA, % 63 60 39 38 52 69 77 85
86
12L14 HR
n
0.26 0.27 0.29 0.30 0.26 0.20 0.16 0.13
0.18
K
f
, MPa
(ksi)
1130
(164)
. . . . . . . . . . . . . . . 585 (85) 435 (63)
400 (58)
TS, MPa
(ksi)
605 (88)
. . . . . . . . . . . . . . . 360 (53) 295 (43)
205 (30)
YS, MPa
(ksi)
240 (35)
. . . . . . . . . . . . . . . 215 (31) 220 (32)
62 (9.0)
RA, % 69 . . . . . . . . . . . . . . . 94 95
94
1524 N
n
0.25 . . . . . . . . . . . . . . . 0.16 0.11
0.30
K
f
, MPa
(ksi)
1380
(200)
1100
(159)
1055
(153)
1195
(173)
1050
(152)
965
(140)
785
(114)
600 (87)
365 (53)
1541 HR
TS, MPa
(ksi)
820
(119)
685 (99)
660 (96)
695
(101)
650 (94)
570 (83) 470 (68) 350 (51)
195 (28)

YS, MPa
(ksi)
415 (60)
380 (55)
380 (55)
330 (48)
360 (52)
295 (43) 275 (40) 250 (36)
70 (10)
RA, % 59 59 45 48 77 87 86 93
97
n 0.19 0.17 0.17 0.20 0.16 0.16 0.15 0.14 0.27
(a)
HR, hot rolled; N, normalized.
(b)
K
f
, strength coefficient; TS, tensile strength; YS, yield strength; RA, reduction of area; n, strain-hardening exponent
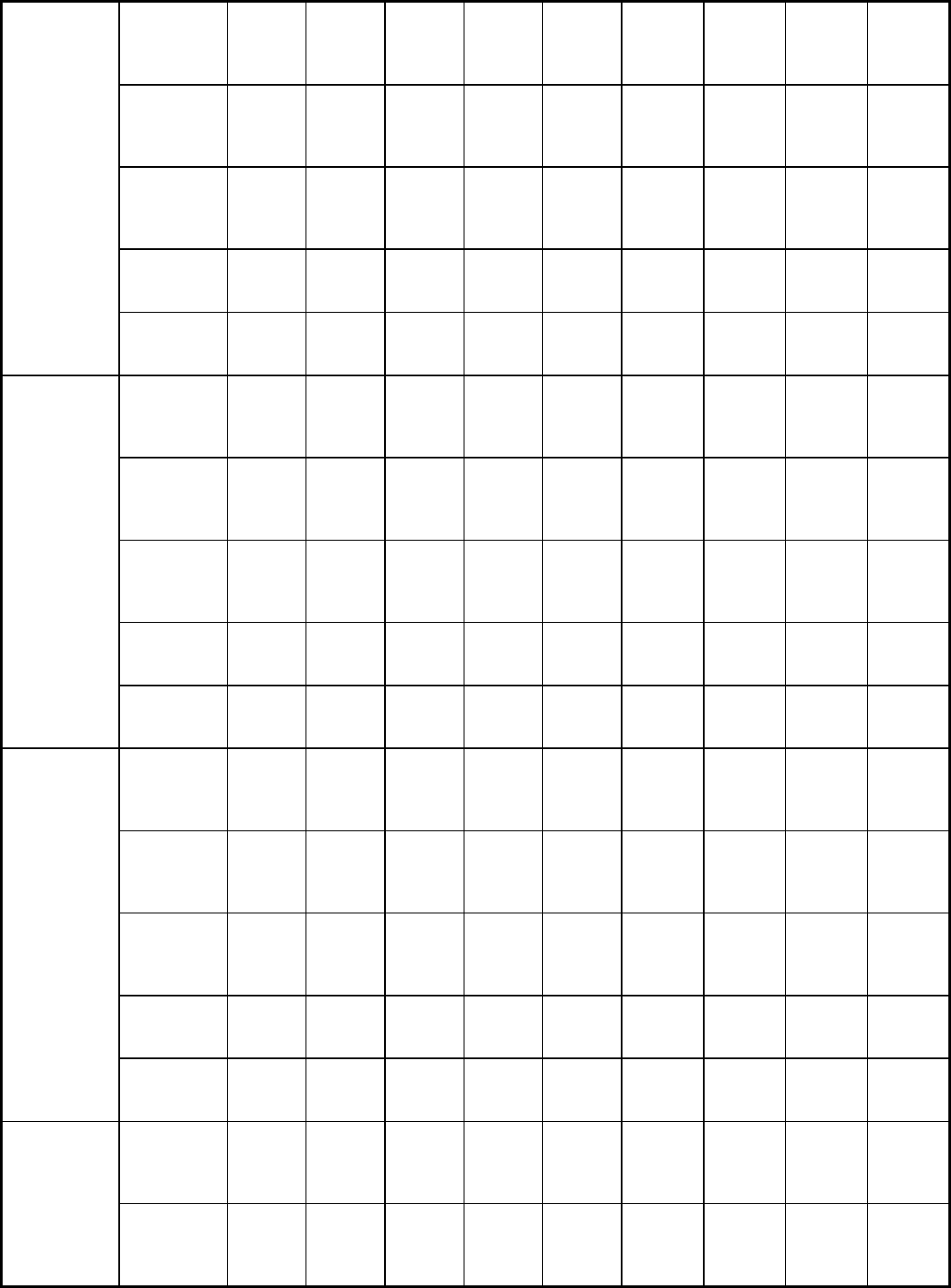
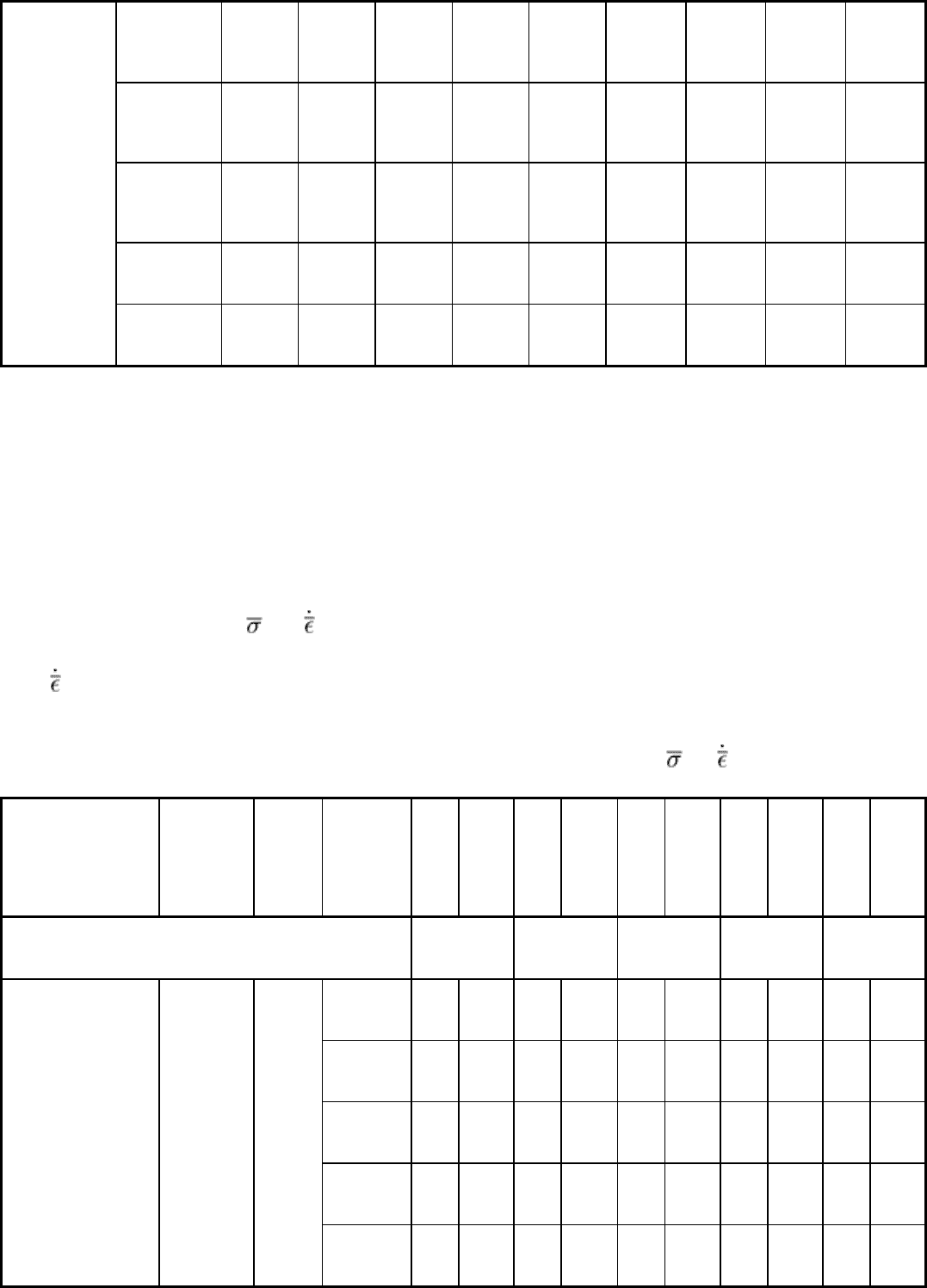
Table 2 Mechanical properties of alloy steels
Average strain rate: 8 mm/mm/s (8 in/in/s). Source: Ref 2
Testing temperature, °C (°F)
Steel grade
and
condition
(a)
Property
(b)
25 (75) 205
(400)
400
(750)
455
(850)
510
(950)
565
(1050)
620
(1150)
675
(1250)
815
(1500)
K
f
, MPa
(ksi)
1140
(165)
. . . . . . . . . . . . 795
(115)
745
(108)
685 (99)
420 (61)
TS, MPa
(ksi)
650 (94)
. . . . . . . . . . . . 485 (70) 405 (59) 330 (48)
205 (30)
YS, MPa
(ksi)
310 (45)
. . . . . . . . . . . . 275 (40) 240 (35) 270 (39)
75 (11)
RA, % 60 . . . . . . . . . . . . 83 88 91
93
4028 HR
n
0.21 . . . . . . . . . . . . 0.17 0.18 0.15
0.28
K
f
, MPa
(ksi)
1825
(265)
. . . . . . . . . . . . . . . 925
(134)
625 (97)
425 (62)
TS, MPa
(ksi)
1040
(151)
. . . . . . . . . . . . . . . 560 (81) 425 (62)
220 (32)
YS, MPa
(ksi)
560 (81)
. . . . . . . . . . . . . . . 325 (47) 260 (38)
65 (9.6)
RA, % 46 . . . . . . . . . . . . . . . 88 93
94
4137 HR
n
0.19 . . . . . . . . . . . . . . . 0.17 0.15
0.30
K
f
, MPa
(ksi)
1070
(155)
820
(119)
740
(107)
765
(111)
780
(113)
725
(105)
635 (92) 495 (72)
400 (58)
TS, MPa
(ksi)
620 (90)
495 (72)
460 (67)
485 (70)
475 (69)
435 (63) 395 (57) 310 (45)
205 (30)
YS, MPa
(ksi)
330 (48)
295 (43)
315 (46)
324 (47)
295 (43)
260 (38) 260 (38) 205 (30)
75 (11)
RA, % 67 70 68 69 73 82 88 93
95
4140 SA
n
0.19 0.17 0.15 0.15 0.16 0.16 0.14 0.14
0.27
K
f
, MPa
(ksi)
1875
(272)
1825
(265)
1985
(288)
1570
(228)
1270
(184)
1145
(166)
995
(144)
650 (94)
385 (56)
TS, MPa
(ksi)
1145
(166)
1070
(155)
965
(140)
915
(133)
820
(119)
705
(102)
600 (87) 440 (64)
200 (29)
YS, MPa
(ksi)
738
(107)
700
(101)
495 (72)
585 (85)
560 (81)
485 (70) 415 (60) 310 (45)
75 (11)
RA, % 52 52 43 57 67 76 87 93
94
4340 HR
n
0.15 0.16 0.22 0.16 0.13 0.14 0.14 0.12
0.26
K
f
, MPa
(ksi)
1165
(169)
. . . . . . . . . . . . . . . 635 (92) 435 (63)
385 (56)
TS, MPa
(ksi)
640 (93)
. . . . . . . . . . . . . . . 395 (57) 305 (44)
200 (29)
YS, MPa
(ksi)
275 (40)
. . . . . . . . . . . . . . . 235 (34) 220 (32)
60 (8.7)
RA, % 62 . . . . . . . . . . . . . . . 82 90
86
4620 HR
n
0.23 . . . . . . . . . . . . . . . 0.16 0.11
0.30
K
f
, MPa
(ksi)
985
(143)
. . . . . . . . . . . . 670 (97) 525 (76) 460 (67)
380 (55)
5120 N
TS, MPa
(ksi)
600 (87)
. . . . . . . . . . . . 435 (63) 370 (54) 305 (44)
193 (28)
YS, MPa
(ksi)
305 (44)
. . . . . . . . . . . . 260 (38) 260 (38) 205 (30)
60 (8.5)
RA, % 67 . . . . . . . . . . . . 83 89 93
92
n
0.19 . . . . . . . . . . . . 0.15 0.11 0.13
0.30
K
f
, MPa
(ksi)
1025
(149)
. . . . . . . . . . . . 670 (97) 595 (86) 460 (67)
365 (53)
TS, MPa
(ksi)
605 (88)
. . . . . . . . . . . . 435 (63) 380 (55) 305 (44)
195 (28)
YS, MPa
(ksi)
295 (43)
. . . . . . . . . . . . 260 (38) 220 (32) 205 (30)
65 (9.3)
RA, % 63 . . . . . . . . . . . . 68 81 87
87
51L20 N
n
0.20 . . . . . . . . . . . . 0.15 0.16 0.13
0.28
K
f
, MPa
(ksi)
1150
(167)
930
(135)
1185
(172)
1150
(167)
905
(131)
800
(116)
660 (96) 485 (70)
360 (52)
TS, MPa
(ksi)
710
(103)
1135
(84)
625 (91)
635 (92)
605 (88)
525 (76) 435 (63) 345 (50)
185 (27)
YS, MPa
(ksi)
400 (58)
635 (47)
270 (39)
295 (43)
395 (57)
340 (49) 295 (43) 260 (38)
65 (9.1)
RA, % 60 62 43 44 56 67 77 84
87
8620 HR
n
0.17 0.17 0.24 0.22 0.14 0.14 0.13 0.10
0.26
K
f
, MPa
(ksi)
1100
(160)
903
(131)
895
(130)
950
(138)
945
(137)
795
(115)
620 (90) 560 (81)
425 (62)
TS, MPa
(ksi)
685 (99)
551 (80)
495 (72)
530 (77)
515 (75)
450 (65) 380 (55) 330 (48)
240 (35)
YS, MPa
(ksi)
435 (63)
340 (49)
270 (39)
305 (44)
270 (39)
235 (34) 215 (31) 220 (32)
120 (17)
RA, % 57 60 60 58 67 76 85 90
92
52100 SA
n
0.15 0.16 0.19 0.19 0.20 0.20 0.17 0.15
0.21
K
f
, MPa
(ksi)
1475
(214)
. . . . . . . . . . . . 915
(133)
670 (97) 475 (69)
400 (58)
TS, MPa
(ksi)
840
(122)
. . . . . . . . . . . . 525 (76) 435 (63) 345 (50)
205 (30)
YS, MPa
(ksi)
240 (35)
. . . . . . . . . . . . 285 (41) 285 (41) 255 (37)
65 (9.6)
RA, % 48 . . . . . . . . . . . . 89 91 93
94
EX-33 HR
n 0.22 . . . . . . . . . . . . 0.19 0.14 0.10 0.29
(a)
HR, hot rolled; N, normalized; SA, spheroidize-annealed.
(b)
K
f
, strength coefficient; TS, tensile strength; YS, yield strength; RA, reduction of area; n, strain-hardening exponent
At higher temperatures, above the recrystallization temperature, the flow stress is influenced mainly by the strain rate, and
can be approximated as:
= C ( )
m
(Eq 3)
where is the strain rate, and C and m are empirical constants. Strain rate dependent data for numerous steels, aluminum
alloys, and titanium alloys are shown in Table 3, Table 4, and Table 5, respectively.
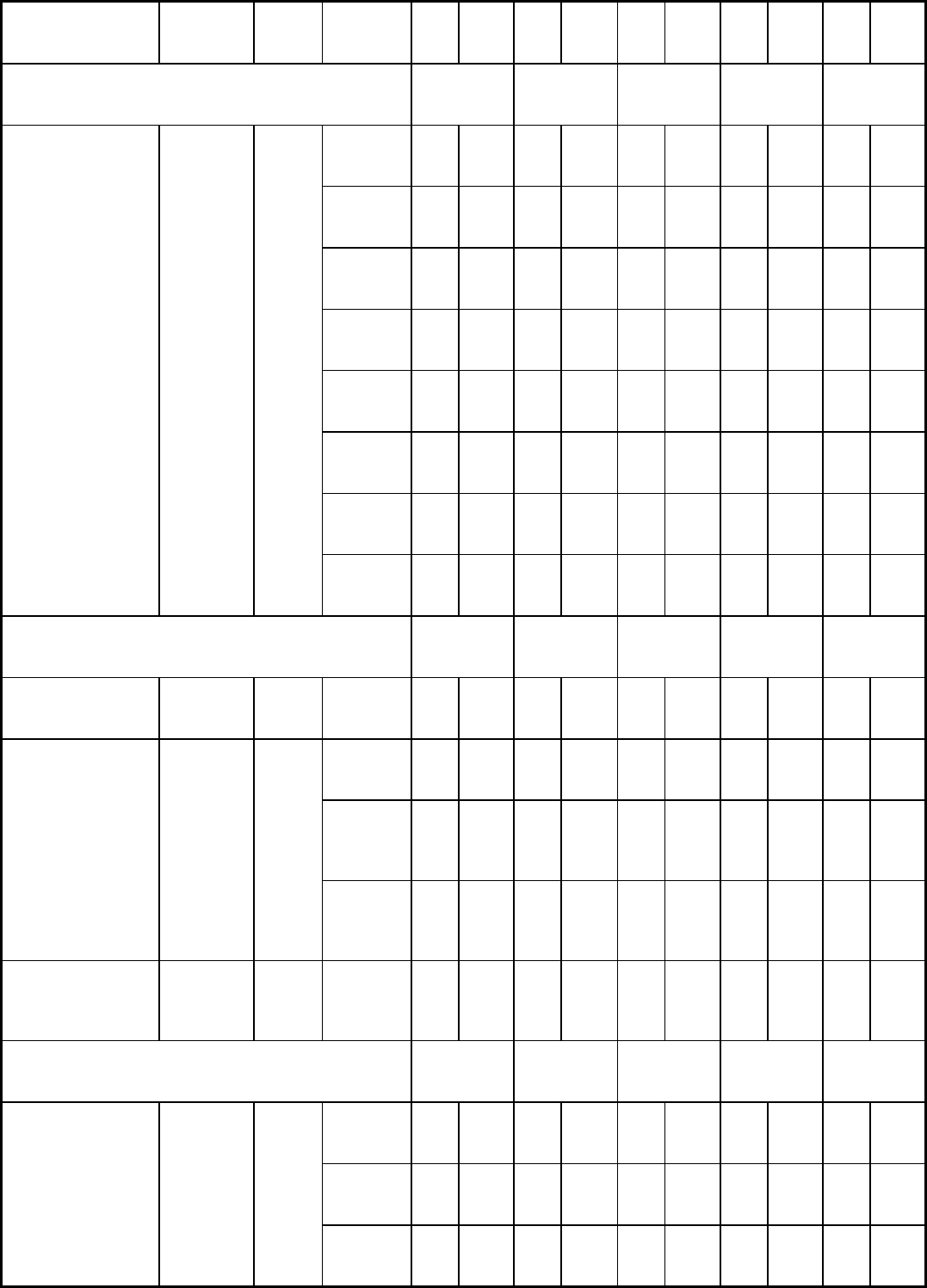
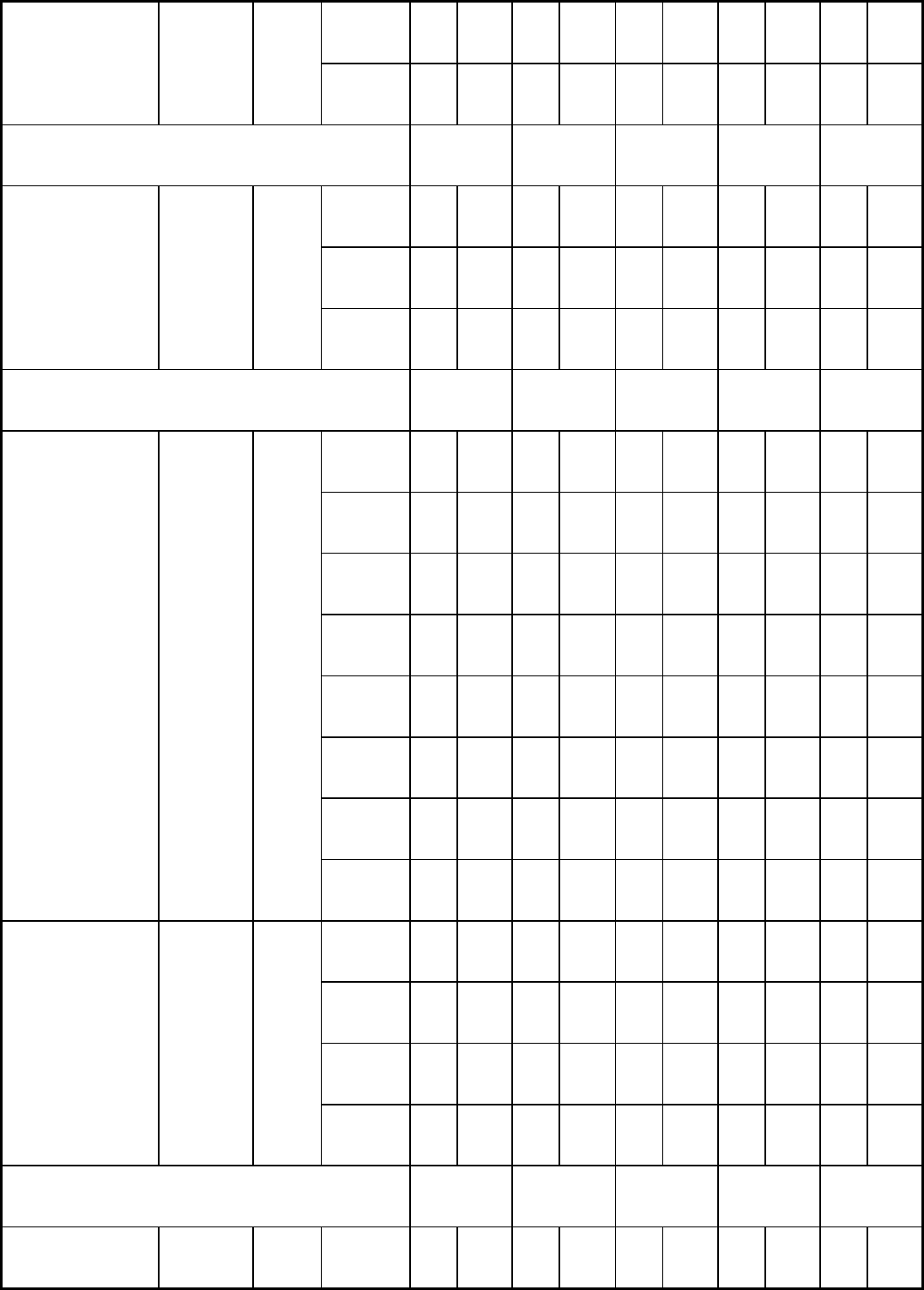
Table 3 Summary of C (ksi) and m values describing the flow stress relation, = C( )
m
, for steels at various
temperatures
Material Material
history
Strain
rate
range,
s
-1
Strain C m C m C m C m C m
Test temperature, °C (°F) 600 (1110) 800 (1470) 1000 (1830) 1200 (2190)
0.2 36.8
0.112
. . . . . . . . . . . . . . . . . . . . .
. . .
0.25 . . . . . . 19.9
0.105
17.0
0.045
7.2 0.137
. . .
. . .
0.4 40.6
0.131
. . . . . . . . . . . . . . . . . . . . .
. . .
0.5 . . . . . . 21.5
0.104
18.8
0.058
6.8 0.169
. . .
. . .
1015 Forged,
annealed
0.2-30
0.6 40.0
0.121
. . . . . . . . . . . . . . . . . . . . .
. . .
0.7 39.5
0.114
21.1
0.109
18.3
0.068
5.7 0.181
. . .
. . .
Test temperature, °C (°F) 900 (1650) 1000 (1830) 1100 (2010) 1200 (2190)
0.05 11.8
0.133
10.7
0.124
9.0 0.117
6.4 0.150
. . .
. . .
0.1 16.5
0.099
13.7
0.099
9.7 0.130
7.1 0.157
. . .
. . .
0.2 20.8
0.082
16.5
0.090
12.1
0.119
9.1 0.140
. . .
. . .
0.3 22.8
0.085
18.2
0.088
13.4
0.109
9.5 0.148
. . .
. . .
0.4 23.0
0.084
18.2
0.098
12.9
0.126
9.1 0.164
. . .
. . .
0.5 23.9
0.088
18.1
0.109
12.5
0.141
8.2 0.189
. . .
. . .
0.6 23.3
0.097
16.9
0.127
12.1
0.156
7.8 0.205
. . .
. . .
1016 Hot rolled,
annealed
. . .
0.7 22.8
0.104
17.1
0.127
12.4
0.151
8.1 0.196
. . .
. . .
Test temperature, °C (°F) 870 (1600) 980 (1800) 1090 (2000) 1205 (2200)
1180 (2150)
1018 . . . . . . . . . 25.2
0.07 15.8
0.152
11.0
0.192
9.2 0.20 . . .
. . .
0.25 . . . . . . 33.7
0.004
16.2
0.075
9.3 0.077
. . .
. . .
0.50 . . . . . . 41.4
-
0.032
17.2
0.080
9.6 0.094
. . .
. . .
1025 Forged,
annealed
3.5-30
0.70 . . . . . . 41.6
-
0.032
17.5
0.082
8.8 0.105
. . .
. . .
1043 Hot rolled,
as-received
0.1-
100
0.3/0.5/0.7
. . . . . . . . . . . . . . . . . . . . . . . . 10.8
0.21
Test temperature, °C (°F) 900 (1650) 1000 (1830) 1100 (2010) 1200 (2190)
0.05 25.4
0.080
15.1
0.089
11.2
0.100
8.0 0.175
. . .
. . .
0.10 28.9
0.082
18.8
0.103
13.5
0.125
9.4 0.168
. . .
. . .
1045 . . . . . .
0.20 33.3
0.086
22.8
0.108
15.4
0.128
10.5
0.167
. . .
. . .
0.30 35.4
0.083
24.6
0.110
15.8
0.162
10.8
0.180
. . .
. . .
0.40 35.4
0.105
24.7
0.134
15.5
0.173
10.8
0.188
. . .
. . .
Test temperature, °C (°F) 600 (1110) 800 (1470) 1000 (1830) 1200 (2190)
. . . . . . . . . 29.4
0.087
14.9
0.126
7.4 0.145
. . .
. . .
. . . . . . . . . 32.5
0.076
13.3
0.191
7.4 0.178
. . .
. . .
1055 Forged,
annealed
3.5-30
. . . . . . . . . 32.7
0.066
11.5
0.237
6.4 0.229
. . .
. . .
Test temperature, °C (°F) 900 (1650) 1000 (1830) 1100 (2010) 1200 (2190)
0.05 16.2
0.128
10.8
0.168
8.7 0.161
6.5 0.190
. . .
. . .
0.10 18.3
0.127
13.2
0.145
10.1
0.149
7.5 0.165
. . .
. . .
0.20 21.8
0.119
16.1
0.125
12.1
0.126
8.5 0.157
. . .
. . .
0.30 23.3
0.114
17.1
0.125
12.8
0.132
8.8 0.164
. . .
. . .
0.40 23.7
0.112
16.8
0.128
12.5
0.146
8.8 0.171
. . .
. . .
0.50 23.6
0.110
16.6
0.133
12.7
0.143
8.7 0.176
. . .
. . .
0.60 22.8
0.129
17.1
0.127
11.7
0.169
8.4 0.189
. . .
. . .
1060 . . . . . .
0.70 21.3
0.129
16.2
0.138
10.7
0.181
7.8 0.204
. . .
. . .
0.10 18.3
0.146
13.9
0.143
9.8 0.159
7.1 0.184
. . .
. . .
0.30 21.9
0.133
16.6
0.132
11.7
0.147
8.0 0.183
. . .
. . .
0.50 21.8
0.130
15.7
0.151
10.6
0.176
7.3 0.209
. . .
. . .
1095 Hot rolled,
annealed
1.5-
100
0.70 21.0
0.128
13.6
0.179
9.7 0.191
6.5 0.232
. . .
. . .
Test temperature, °C (°F) 930 (1705) 1000 (1830) 1060 (1940) 1135 (2075)
1200 (2190)
1115 Hot rolled,
as-received
4.4-
23.1
0.105 16.3
0.088
13.0
0.108
10.9
0.112
9.1 0.123
7.6
0.116
