Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


268 Chapter 4
4.10. We again consider the telegraph partial differential equation over the finite interval
I ={x |0 <x<1}.
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
−ζu(x, t)
with c = 1/4,γ = 1/5,ζ = 1/10, and boundary conditions
u(0,t)= 0 and u
x
(1,t)= 0
The left end of the string is secured and the right end of the string is unsecured. The
initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Use the method of separation of variables to evaluate the eigenvalues and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate
the solution for each of the three sets of initial conditions given:
f 1(x) =
x −
1
2
2
and g1(x) = 0
f 2(x) = x and g2(x) = 1
f 3(x) = x
1 −
x
2
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.11. We again consider the telegraph partial differential equation over the finite interval
I ={x |0 <x<1}.
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
−ζu(x, t)
with c = 1/4,γ = 1/5,ζ = 1/10, and boundary conditions
u(0,t)= 0 and u
x
(1,t)+u(1,t)= 0
The left end of the string is secured, and the right end of the string is attached to an
elastic hinge. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)

The Wave Partial Differential Equation 269
Use the method of separation of variables to evaluate the eigenvalues and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate
the solution for each of the three sets of initial conditions given:
f 1(x) = 1 and g1(x) = 0
f 2(x) = x and g2(x) = 1
f 3(x) = x
1 −
2x
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.12. We again consider the telegraph partial differential equation over the finite interval
I ={x |0 <x<1}. The telegraph equation reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
−ζu(x, t)
with c = 1/4,γ = 1/5,ζ = 1/10, and boundary conditions
u
x
(0,t)−u(0,t)= 0 and u(1,t)= 0
The left end of the string is attached to an elastic hinge, and the right end of the string is
secured. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Use the method of separation of variables to evaluate the eigenvalues and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate
the solution for each of the three sets of initial conditions given:
f 1(x) = 1 and g1(x) = 0
f 2(x) = 1 −x and g2(x) = 1
f 3(x) =−
2x
2
3
+
x
3
+
1
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.13. Here, we consider the transverse wave motion along a taut string over the finite interval
I ={x |0 <x<1}. The damping on the string is negligible, and the string is immersed
in a medium that provides a restoring force that is proportional to the displacement of

270 Chapter 4
the string (Hooke’s law–type of force). The resulting partial differential equation is
called the “Klein-Gordon” equation:
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−ζu(x, t)
with c = 1/4,ζ = 1/10, and boundary conditions
u
x
(0,t)= 0 and u(1,t)= 0
The left end of the string is unsecured and the right end of the string is secured. The
initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Use the method of separation of variables to evaluate the eigenvalues and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate
the solution for each of the three sets of initial conditions given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 and g2(x) = 1
f 3(x) = 1 −x
2
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.14. We again consider the Klein-Gordon equation for transverse wave motion along a taut
string over the finite interval I ={x |0 <x<1}. The Klein-Gordon equation reads
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−ζu(x, t)
with c = 1/4,ζ = 1/10, and boundary conditions
u
x
(0,t)= 0 and u
x
(1,t)+u(1,t)= 0
The left end of the string is unsecured, and the right end of the string is attached to an
elastic hinge. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Use the method of separation of variables to evaluate the eigenvalues and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate

The Wave Partial Differential Equation 271
the solution for each of the three sets of initial conditions given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 and g2(x) = 1
f 3(x) = 1 −
x
2
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.15. We again consider the Klein-Gordon equation for transverse wave motion along a taut
string over the finite interval I ={x |0 <x<1}. The Klein-Gordon equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−ζu(x, t)
with c = 1/4,ζ = 1/10, and boundary conditions
u
x
(0,t)−u(0,t)= 0 and u
x
(1,t)= 0
The left end of the string is attached to an elastic hinge, and the right end of the string is
unsecured. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Use the method of separation of variables to evaluate the eigenvalues, and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate
the solution for each of the three sets of initial conditions given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 and g2(x) = 1
f 3(x) = 1 −
(x −1)
2
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
Exercises in Cylindrical Coordinates
4.16. Consider the transverse vibrations in a thin circularly symmetric membrane over the
finite interval I ={r |0 <r<1 with a slight amount of damping. The homogeneous
partial differential equation reads as
∂
2
∂t
2
u(r, t) =
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
−γ
∂
∂t
u(r, t)

272 Chapter 4
with c = 1/4,γ = 1/5, and boundary conditions
|u(0,t)| < ∞ and u(1,t)= 0
The center of the membrane has a finite amplitude, and the periphery of the membrane
is secure. The initial conditions are
u(r, 0) = f(r) and u
t
(r, 0) = g(r)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for the three sets of initial conditions given:
f 1(r) = r
2
and g1(r) = 0
f 2(r) = 1 and g2(r) = 1
f 3(r) = 1 −r
2
and g3(r) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.17. Consider the transverse vibrations in a thin circularly symmetric membrane over the
finite interval I ={r |0 <r<1} with a slight amount of damping. The homogeneous
partial differential equation reads as
∂
2
∂t
2
u(r, t) =
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
−γ
∂
∂t
u(r, t)
with c = 1/4,γ = 1/5, and boundary conditions
|u(0,t)| < ∞ and u
r
(1,t)= 0
The center of the membrane has a finite amplitude, and the periphery of the membrane
is unsecured. The initial conditions are
u(r, 0) = f(r) and u
t
(r, 0) = g(r)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for the three sets of initial conditions given:
f 1(r) = r
2
and g1(r) = 0
f 2(r) = 1 and g2(r) = 1
f 3(r) = r
2
−
r
4
2
and g3(r) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.

The Wave Partial Differential Equation 273
4.18. Consider the transverse vibrations in a thin circularly symmetric membrane over the
finite interval I ={r |0 <r<1} with a slight amount of damping. The homogeneous
partial differential equation reads as
∂
2
∂t
2
u(r, t) =
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
−γ
∂
∂t
u(r, t)
with c = 1/4,γ = 1/5, and boundary conditions
|u(0,t)| < ∞ and u
r
(1,t)+u(1,t)= 0
The center of the membrane has a finite amplitude, and the periphery of the membrane
is attached to an elastic hinge. The initial conditions are
u(r, 0) = f(r) and u
t
(r, 0) = g(r)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
out the general solution. Evaluate the solution for the three sets of initial conditions
given:
f 1(r) = r
2
and g1(r) = 0
f 2(r) = 1 and g2(r) = 1
f 3(r) = 1 −
r
2
3
and g3(r) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
Significance of Wave Speed
The speed of propagation of the wave in the preceding exercises was indicated by the
factor c. (This speed is not to be confused with the speed of motion of the particles that
make up the medium and whose collective motion constitutes the wave.) In the
preceding exercises, we assumed the medium to be homogeneous and isotropic so that
all terms that evaluate c are treated as constants.
In the case of transverse waves on a taut string, the constant c is given as
c =
To
ρ
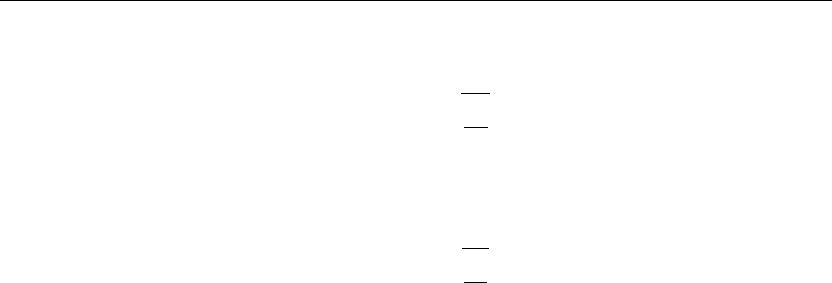
274 Chapter 4
where To is the tension in the string and ρ is the linear density of the string. In the case
of longitudinal waves in a bar, the constant c is given as
c =
Eo
ρ
where Eo is the Young’s modulus of elasticity and ρ is the mass density of the bar. In
the case of transverse waves in a membrane, the constant c is given as
c =
To
ρ
where To is the tension per unit length in the membrane and ρ is the areal density (mass
per unit area) of the membrane. In the MKS system, wave speed has dimensions of
meters per second.
In the following exercises, you are asked to multiply the speed term by a given factor
and to develop the solution for the initial conditions set {f 3(x), g3(x)}. Develop the
animated solution, and take particular note of how the increase in wave speed affects
the vibration frequency of the various modes of vibration of the medium.
4.19. In Exercise 4.2, multiply the speed term c by a factor of 2 and solve.
4.20. In Exercise 4.4, multiply the speed term c by a factor of 4 and solve.
4.21. In Exercise 4.7, multiply the speed term c by a factor of 2 and solve.
4.22. In Exercise 4.9, multiply the speed term c by a factor of 4 and solve.
4.23. In Exercise 4.13, multiply the speed term c by a factor of 2 and solve.
4.24. In Exercise 4.16, multiply the speed term c by a factor of 4 and solve.
4.25. In Exercise 4.17, multiply the speed term c by a factor of 2 and solve.

CHAPTER 5
The Laplace Partial Differential
Equation
5.1 Introduction
The Laplace partial differential equation can be shown to be the steady-state equivalent of
either the wave equation or the diffusion equation. In electrostatics, the Laplace equation
describes the potential in a charge-free region, and, for this reason, it is sometimes called the
“potential” equation.
In Chapter 3, we discussed the diffusion or heat partial differential equation in rectangular
coordinates in one spatial dimension with no internal sources. If we view the spatial derivative
operator as the first term of the Laplacian operator, then an extension of this diffusion
equation from one to two spatial dimensions reads
∂
∂t
u(x, y, t) = k
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
If we consider the steady-state or time-invariant version of this equation, we get
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The preceding partial differential equation is the familiar homogeneous Laplace partial
differential equation in the two-dimensional rectangular coordinate system.
In Chapter 4, we discussed the wave partial differential equation in rectangular coordinates in
one spatial dimension with no damping in the system and no external applied forces. Again, if
we view the spatial derivative operator as the first term of the Laplacian operator, then an
extension of the wave equation from one to two spatial dimensions reads
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
© 2009, 2003, 1999 Elsevier Inc. 275

276 Chapter 5
Again, if we consider the steady-state or time-invariant version of this equation, we get
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
Thus, we see that in the steady-state situation, both the diffusion and the wave partial
differential equation reduce to the familiar Laplace equation.
A typical example steady-state problem is as follows. We seek the steady-state temperature
distribution u(x,y) in a thin plate over the rectangular domain D ={(x,y) |0 <x<1,
0 <y<1}. The lateral surfaces of the plate are insulated so that no heat escapes from the
lateral surfaces. The sides y = 0 and y = 1 are insulated, the side x = 1 has a fixed temperature
of zero, and the side x = 0 has a temperature distribution f(y) given as follows.
The Laplace partial differential equation that describes the steady-state temperature in the
plate is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
Because the sides y = 0 and y = 1 are insulated, the side x = 0 is at a fixed temperature zero,
and the side x = 0 has a given temperature distribution, the boundary conditions on the
problem are
u(0,y)= f(y) and u(1,y)= 0
and
u
y
(x, 0) = 0 and u
y
(x, 1) = 0
We develop the solution for this problem in Section 5.3 later.
5.2 Laplace Equation in the Rectangular Coordinate System
We now focus on the solution to the Laplace equation over the finite two-dimensional domain
D ={(x,y) |0 <x<a,0 <y<b} in rectangular coordinates. From the preceding section,
the relevant partial differential equation can be rewritten to read
∂
2
∂x
2
u(x, y) =−
∂
2
∂y
2
u(x, y)
Based on our success in solving the diffusion equation and the wave equation in Chapters 3
and 4, we use the method of separation of variables to solve this equation. We set
u(x, y) = X(x)Y(y)

The Laplace Par tial Differential Equation 277
Substituting this assumed solution into the partial differential equation, we get
d
2
dx
2
X(x)
Y(y) =−X(x)
d
2
dy
2
Y(y)
Dividing the preceding by the product solution yields
d
2
dx
2
X(x)
X(x)
=−
d
2
dy
2
Y(y)
Y(y)
Because the left-hand side of the equation is an exclusive function of x and the right-hand side
is an exclusive function of y, and x and y are independent, then in order for the equation to
hold for all x and y, we must set each side equal to a constant λ. Doing so gives us the
following two ordinary differential equations:
d
2
dx
2
X(x)+λX(x) = 0
and
d
2
dy
2
Y(y) −λY(y) = 0
Both of these ordinary differential equations are of the Euler type. To proceed further, we now
consider the boundary conditions on the problem. Generally, one seeks a solution to this
problem over the finite two-dimensional domain D ={(x,y) |0 <x<a,0 <y<b} subject to
the regular homogeneous boundary conditions on one of the variables, x or y. We seek that
variable whose boundary conditions are homogeneous.
For example, consider the case where the boundary conditions on u(x,y) are homogeneous
with respect to the x variable:
κ
1
u(0,y)+κ
2
u
x
(0,y)= 0
and
κ
3
u(a, y) +κ
4
u
x
(a, y) = 0 (5.1)
The earlier ordinary differential equation in x, combined with the equivalent homogeneous
boundary conditions, constitutes a Sturm-Liouville problem in the variable x, for which we
already have solutions.
