Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


278 Chapter 5
5.3 Sturm-Liouville Problem for the Laplace Equation in
Rectangular Coordinates
The differential equation in the spatial variable x in the preceding equation must be solved
subject to the equivalent homogeneous spatial boundary conditions over the finite interval. The
Sturm-Liouville problem for the x-dependent equation consists of the ordinary differential
equation
d
2
dx
2
X(x)+λX(x) = 0
along with the equivalent corresponding homogeneous boundary conditions on the x variable
as shown here:
κ
1
X(0) +κ
2
X
x
(0) = 0
and
κ
3
X(a)+κ
4
X
x
(a) = 0
We recognize this problem in the spatial variable x to be a regular Sturm-Liouville eigenvalue
problem whereby the allowed values of λ are called the system “eigenvalues” and the
corresponding solutions are called the “eigenfunctions.” Note that the preceding ordinary
differential equation is of the Euler type with the weight function w(x) = 1.
As before, it can be shown that for regular Sturm-Liouville problems over finite domains, an
infinite number of eigenvalues exists that can be indexed by the integer numbers n. The
indexed eigenvalues and corresponding eigenfunctions are given, respectively, as
λ
n
,X
n
(x)
for n = 0, 1, 2, 3,....
From the stated properties of regular Sturm-Liouville eigenvalue problems in Section 2.1, the
eigenfunctions form a “complete” set with respect to any piecewise smooth function over the
finite x-dependent interval I ={x |0 <x<a}.
From Section 1.4 on second-order linear differential equations, the solution to the
corresponding y-dependent differential equation in terms of the allowed eigenvalues is
Y
n
(y) = A(n) cosh
λ
n
y
+B(n) sinh
λ
n
y
Thus, for each allowed value of the index n, we have a solution
u
n
(x, y) = X
n
(x)
A(n) cosh
λ
n
y
+B(n) sinh
λ
n
y
for n = 0, 1, 2, 3,....
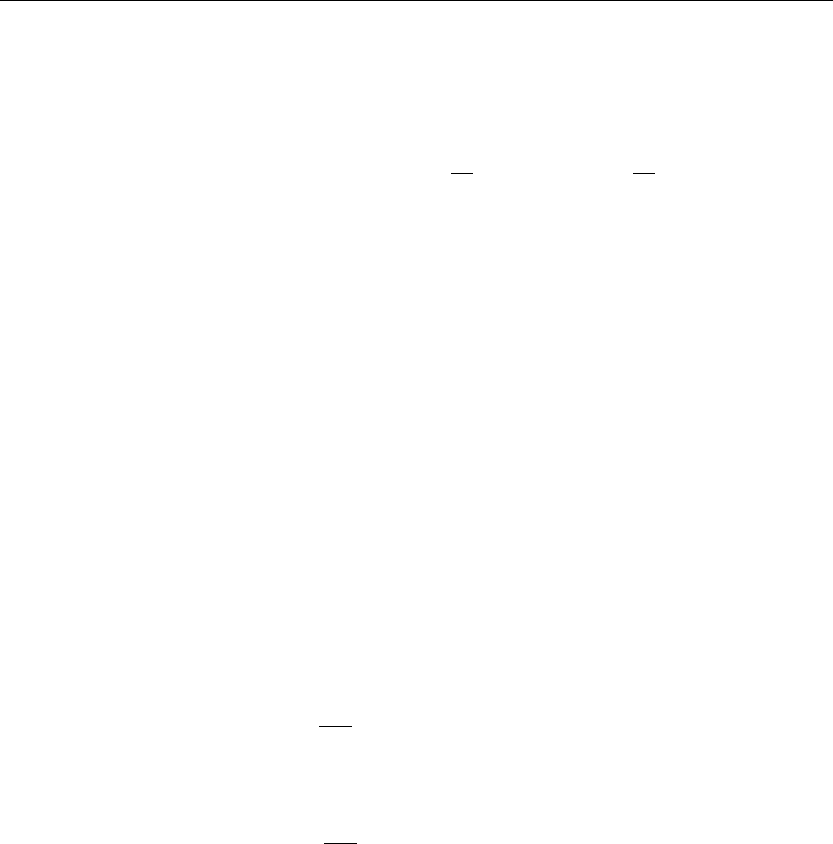
The Laplace Par tial Differential Equation 279
These functions form a set of basis vectors for the solution space of the partial differential
equation. Using the same concepts of the superposition principle as in Chapters 3 and 4, the
general solution to the homogeneous partial differential equation can now be written as an
infinite sum over all basis vectors as follows:
u(x, y) =
∞
n=0
X
n
(x)
A(n) cosh
λ
n
y
+B(n) sinh
λ
n
y
The arbitrary constants A(n) and B(n) are evaluated by taking advantage of the orthonormality
of the x-dependent eigenfunctions over the finite interval I ={x |0 <x<a}, with respect to
the weight function w(x) = 1. The statement of orthonormality reads
a
0
X
n
(x)X
m
(x)dx = δ(n, m)
for n, m = 0, 1, 2, 3,....
We mentioned earlier that in using the method of separation of variables successfully, we must
seek out that variable, x or y, that experiences the homogeneous boundary conditions. In the
preceding, conditions on x forced it to be that variable.
We now consider the alternative possibility. If the homogeneous boundary conditions on
u(x,y) are on the variable y instead of x, then we rewrite the two earlier ordinary differential
equations as
d
2
dx
2
X(x)−λX(x) = 0
and
d
2
dy
2
Y(y) +λY(y) = 0
The homogeneous boundary conditions on u(x,y) with respect to the variable y are as shown:
κ
1
u(x, 0) +κ
2
u
y
(x, 0) = 0
and
κ
3
u(x, b) +κ
4
u
y
(x, b) = 0
The given ordinary differential equation on y, combined with the preceding equivalent regular
homogeneous boundary conditions, again constitutes a Sturm-Liouville problem, in terms of
the variable y, for which we already have solutions.

280 Chapter 5
The differential equation in the spatial variable y must be solved subject to the homogeneous
spatial boundary conditions over the finite interval. The Sturm-Liouville problem for the
y-dependent equation consists of the ordinary differential equation
d
2
dy
2
Y(y) +λY(y) = 0
along with the equivalent corresponding homogeneous boundary conditions on y shown:
κ
1
Y(0) +κ
2
Y
y
(0) = 0
and
κ
3
Y(b) +κ
4
Y
y
(b) = 0
Again, we see this problem in the spatial variable y to be a regular Sturm-Liouville eigenvalue
problem whereby the allowed values of λ are called the system “eigenvalues” and the
corresponding solutions are called the “eigenfunctions.” Note that the preceding ordinary
differential equation is of the Euler type and the weight function is w(y) = 1.
As before, we can show that for regular Sturm-Liouville problems over finite domains, an
infinite number of eigenvalues exist that can be indexed by the positive integers n. The indexed
eigenvalues and corresponding eigenfunctions are given, respectively, as
λ
n
,Y
n
(y)
for n = 0, 1, 2, 3,....
Again, from the stated properties of regular Sturm-Liouville eigenvalue problems in
Section 2.1, the eigenfunctions form a “complete” set with respect to any piecewise smooth
function over the finite y-dependent interval I ={y |0 <y<b}.
From Section 1.4 on second-order linear differential equations, the solution to the
corresponding x-dependent differential equation in terms of the allowed eigenvalues is
X
n
(x) = A(n) cosh
λ
n
x
+B(n) sinh
λ
n
x
(5.2)
Thus, for each allowed value of the index n, we have a solution
u
n
(x, y) = Y
n
(y)
A(n) cosh
√
λx
+B(n) sinh
√
λx
for n = 0, 1, 2, 3,....
Using the concept of the superposition principle as in Chapters 3 and 4, the general solution to
the homogeneous partial differential equation can again be written as the infinite sum of the
preceding basis vectors in terms of the eigenfunctions with respect to the variable y as follows:
u(x, y) =
∞
n=0
Y
n
(y)
A(n) cosh
λ
n
x
+B(n) sinh
λ
n
x
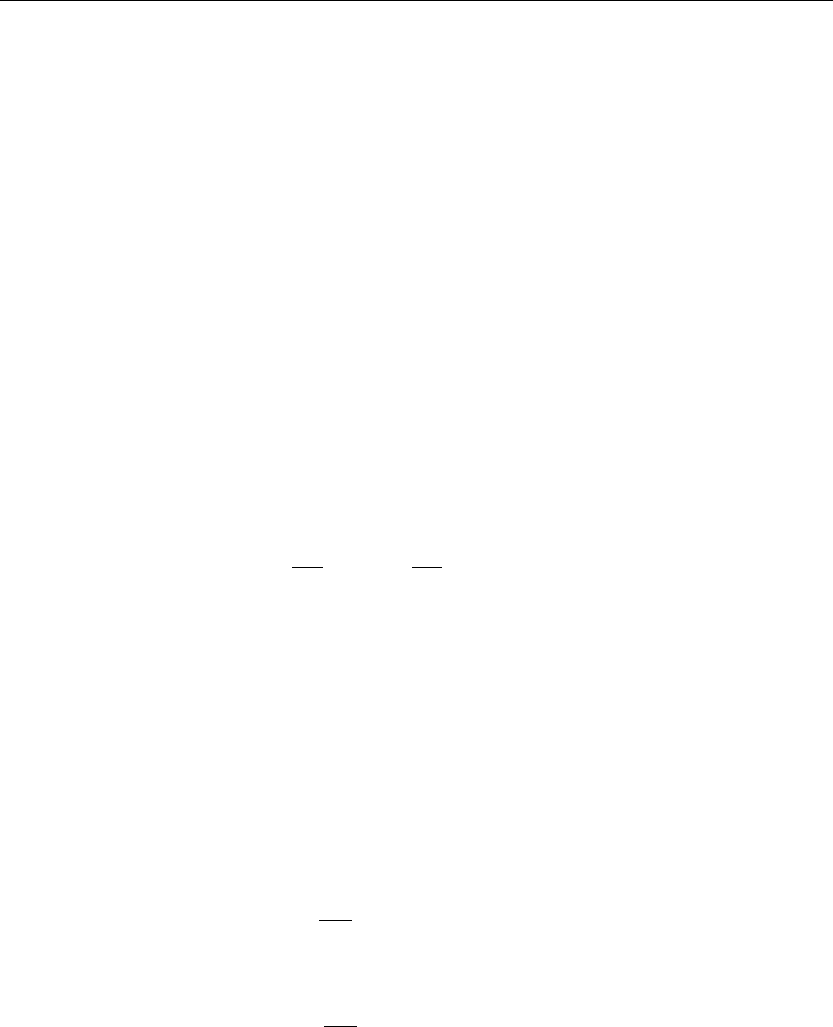
The Laplace Par tial Differential Equation 281
Again, the arbitrary constants A(n) and B(n) can be evaluated by taking advantage of the
orthonormality of the y-dependent eigenfunctions, with respect to the weight function
w(y) = 1 over the interval I ={y |0 <y<b}. The statement of orthonormality reads
b
0
Y
n
(y)Y
m
(y)dy = δ(n, m) (5.3)
for n, m = 0, 1, 2, 3,....
The boundary conditions on the problem determine whether the solution is written in terms of
the eigenfunctions with respect to x or y. Remember that the decision comes from our seeking
that particular variable that experiences the homogeneous boundary conditions.
DEMONSTRATION: We seek the steady-state temperature distribution in a thin rectangular
plate over the rectangular domain D ={(x,y) |0 <x<1, 0 <y<1}. The lateral surfaces of
the plate are insulated. The sides y = 0 and y = 1 are insulated. The side x = 1 has a fixed
temperature of zero, and the side x = 0 has a temperature distribution f(y) given as follows.
SOLUTION: The Laplace partial differential equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The boundary conditions are
u(0,y)= f(y) and u(1,y)= 0
and
u
y
(x, 0) = 0 and u
y
(x, 1) = 0
We seek that variable whose boundary conditions are homogeneous. Here, we see that the
homogeneous boundary conditions are with respect to the y variable. Thus, by the method of
separation of variables, we write the two ordinary differential equations as
d
2
dx
2
X(x)−λX(x) = 0
and
d
2
dy
2
Y(y) +λY(y) = 0
Because both ends along the y-axis are insulated, the corresponding homogeneous boundary
conditions on the y equation are type 2 at y = 0 and type 2 at y = 1.
Y
y
(0) = 0 and Y
y
(1) = 0

282 Chapter 5
The allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Example 2.5.3 in Chapter 2. For λ
0
= 0, we got
Y
0
(y) = 1
and for λ
n
= n
2
π
2
,wegot
Y
n
(y) =
√
2 cos(nπy)
for n = 1, 2, 3,....
The statement of orthonormality with respect to the weight function w(y) = 1 reads
1
0
2 cos(nπy) cos(mπy) dy = δ(n, m)
for n, m = 1, 2, 3,....
A set of basis vectors for the x-dependent equation for λ
n
= n
2
π
2
reads
x1(x) = sinh(nπ(1 −x))
and
x2(x) = cosh(nπ(1 −x))
and the general solution to the x equation is
X
n
(x) = A(n) cosh(nπ(1 −x)) +B(n) sinh(nπ(1 −x))
Substitution of the boundary condition at x = 1 yields A(n) = 0. Thus, the solution for the
x-dependent equation is
X
n
(x) = B(n) sinh(nπ(1 −x))
for n = 1, 2, 3,....
Similarly, for λ
0
= 0, a set of basis vectors is
x1(x) = 1
and
x2(x) = x
and a solution that satisfies the boundary condition at x = 1 reads
X
0
(x) = B(0)(1 −x)
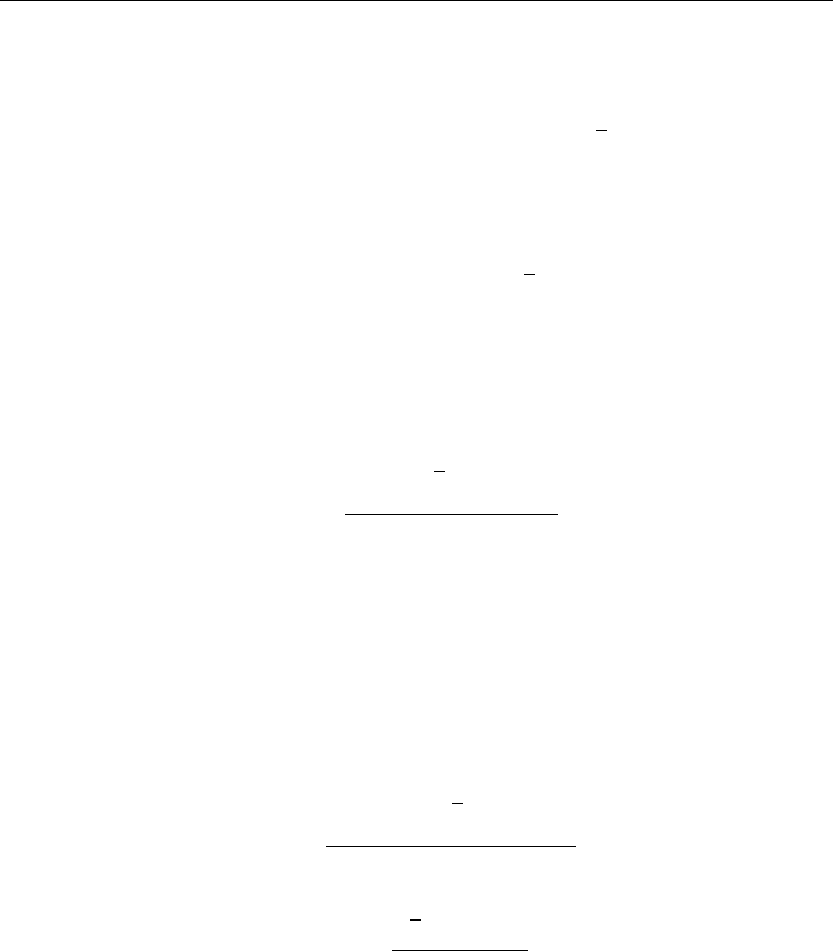
The Laplace Par tial Differential Equation 283
The generalized eigenfunction expansion of the solution is constructed from the sum of the
product of the x-dependent solutions and the preceding orthonormal y-dependent
eigenfunctions. This yields
u(x, y) = B(0)(1 −x) +
∞
n=1
B(n) sinh(nπ(1 −x))
√
2 cos(nπy)
The Fourier coefficients B(n) are determined from the remaining boundary condition.
Substitution of the boundary condition u(0,y)= f(y) at x = 0 yields
f(y) = B(0) +
∞
n=1
B(n) sinh(nπ)
√
2 cos(nπy)
This equation is the Fourier series expansion of f(y) in terms of the orthonormal y-dependent
Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier coefficients B(n),we
take the inner product of both sides with respect to the orthonormal eigenfunctions, and taking
advantage of the statement of orthonormality, we get
B(n) =
1
0
f(y)
√
2 cos(nπy) dy
sinh(nπ)
for n = 1, 2, 3,..., and
B(0) =
1
0
f(y) dy
for n = 0.
We consider the special case for the boundary condition along x = 0tobef(y) = y(1 −y). The
integral for B(n) reads
B(n) =
1
0
y(1 −y)
√
2 cos(nπy) dy
sinh(nπ)
Evaluation of this integral yields
B(n) =−
√
2
(−1)
n
+1
sinh(nπ)n
2
π
2
for n = 1, 2, 3,....
Similarly, for n = 0, the integral for B(0) reads
B(0) =
1
0
y(1 −y) dy

284 Chapter 5
Evaluation of this integral yields
B(0) =
1
6
Finally, the solution for the steady-state temperature of the system is
u(x, y) =
1 −x
6
+
∞
n=1
−
2
(−1)
n
+1
sinh(nπ(1 −x)) cos(nπy)
sinh(nπ)n
2
π
2
The detailed development of this solution and the graphics are given later in one of the Maple
worksheet examples.
5.4 Example Laplace Problems in the Rectangular
Coordinate System
We look at steady-state solutions to wave and diffusion phenomena in the two-dimensional,
rectangular coordinate (x,y) plane. We assume conditions such that there is no dependence of
the solution on the z coordinate.
EXAMPLE 5.4.1: We seek the electrostatic potential in a charge-free rectangular domain
D ={(x,y) |0 <x<1, 0 <y<1}. The sides x = 0,x= 1, and y = 1 are held at a fixed
potential zero, and the side y = 0 has a potential distribution u(x, 0) = f(x) given below.
SOLUTION: The homogeneous Laplace equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The boundary conditions are
u(0,y)= 0 and u(1,y)= 0
and
u(x, 0) = x(1 −x) and u(x, 1) = 0
Here, we see that the boundary conditions are homogeneous with respect to the x variable.
Ordinary differential equations from the method of separation of variables are
d
2
dx
2
X(x)+λX(x) = 0
and
d
2
dy
2
Y(y) −λY(y) = 0

The Laplace Par tial Differential Equation 285
Homogeneous boundary conditions on the x equation are type 1 at x = 0 and type 1 at x = 1
X(0) = 0 and X(1) = 0
Assignment of system parameters
> restart:with(plots):a:=1:b:=1:
Allowed eigenvalues and corresponding orthonormal eigenfunctions for the x equation are
obtained from Example 2.5.1.
> lambda[n]:=(n*Pi/a)ˆ2;
λ
n
:= n
2
π
2
(5.4)
for n = 1, 2, 3,....
Orthonormal eigenfunctions
> X[n](x):=sqrt(2/a)*sin(n*Pi/a*x);X[n](s):=subs(x=s,X[n](x)):X[m](x):=subs(n=m,X[n](x)):
X
n
(x) :=
√
2 sin(nπx) (5.5)
Statement of orthonormality with respect to the weight function w(x) = 1
> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=0..a)=delta(n,m);
1
0
2 sin(nπx) sin(mπx) dx = δ(n, m) (5.6)
Basis vectors for the y equation
> y1(y):=sinh(sqrt(lambda)*(b−y));y2(y):=cosh(sqrt(lambda)*(b−y));
y1(y) := sinh
√
λ(1 −y)
y2(y) := cosh
√
λ(1 −y)
(5.7)
General solution to the y equation
> Y[n](y):=A(n)*cosh(n*Pi/a*(b−y))+B(n)*sinh(n*Pi/a*(b−y));
Y
n
(y) := A(n) cosh(nπ(1 −y)) +B(n) sinh(nπ(1 −y)) (5.8)
Substituting into the y-dependent boundary condition yields
> eval(subs(y=b,Y[n](y)))=0;
A(n) = 0 (5.9)

286 Chapter 5
The y-dependent solution
> Y[n](y):=B(n)*sinh(n*Pi/a*(b−y));
Y
n
(y) := B(n) sinh(nπ(1 −y)) (5.10)
Generalized series terms
> u[n](x,y):=X[n](x)*Y[n](y);
u
n
(x, y) :=
√
2 sin(nπx)B(n) sinh(nπ(1 −y)) (5.11)
Eigenfunction expansion
> u(x,y):=Sum(u[n](x,y),n=1..infinity);
u(x, y) :=
∞
n=1
√
2 sin(nπx)B(n) sinh(nπ(1 −y)) (5.12)
Evaluation of Fourier coefficients from the specific remaining boundary condition
u(x, 0) = f(x) where
> f(x):=x*(1−x);
f(x) := x(1 −x) (5.13)
Substituting this condition into the earlier solution yields
> f(x)=subs(y=0,u(x,y));
x(1 −x) =
∞
n=1
√
2 sin(nπx)B(n) sinh(nπ) (5.14)
The preceding equation is the Fourier series expansion of f(x) in terms of the orthonormal
Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier cofficients, we take the
inner product of both sides with respect to the orthonormal eigenfunctions, and, taking
advantage of the previous statement of orthonormality, we get
> B(n):=(1/sinh(n*Pi*b/a))*Int(f(x)*X[n](x)*w(x),x=0..a);B(n):=expand(value(%)):
B(n) :=
1
0
x(1 −x)
√
2 sin(nπx) dx
sinh(nπ)
(5.15)
Evaluation of this integral yields
> B(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},B(n)));
B(n) := −
2
√
2
−1 +(−1)
n
sinh(nπ)n
3
π
3
(5.16)

The Laplace Par tial Differential Equation 287
Generalized series terms
> u[n](x,y):=eval(X[n](x)*Y[n](y));
u
n
(x, y) := −
4 sin(nπx)
−1 +(−1)
n
sinh(nπ(1 −y))
sinh(nπ)n
3
π
3
(5.17)
Series solution
> u(x,y):=Sum(u[n](x,y),n=1..infinity);
u(x, y) :=
∞
n=1
−
4 sin(nπx)(−1 +(−1)
n
) sinh(nπ(1 −y))
sinh(nπ)n
3
π
3
(5.18)
First few terms of expansion
> u(x,y):=sum(u[n](x,y),n=1..5):
> plot3d(u(x,y),x=0..a,y=0..b,axes=framed,thickness=1);
0.25
0.15
0.1
0.05
0.2
0
0
0.2
0.4
0.6
0.8
1
1
0.8
0.6
0.4
x
y
0.2
0
Figure 5.1
The three-dimensional surface shown in Figure 5.1 depicts the electrostatic potential
distribution u(x, y) over the rectangular region. Note how the edges of the surface adhere to the
given boundary conditions. The equipotential lines can be obtained from Maple by clicking on
the figure and then choosing the special option “Render the plot using the polygon patch and
contour style” in the graphics bar and then clicking the “redraw” button.
EXAMPLE 5.4.2: We seek the steady-state temperature distribution in a thin rectangular plate
over the domain D ={(x, y) |0 <x<1, 0 <y<1} whose lateral surface is insulated. The
sides y = 0 and y = 1 are insulated, the side x = 1 has a fixed temperature of zero, and the side
x = 0 follows the temperature distribution u(0,y)= f(y) given as follows.
SOLUTION: The homogeneous Laplace equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
