Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.

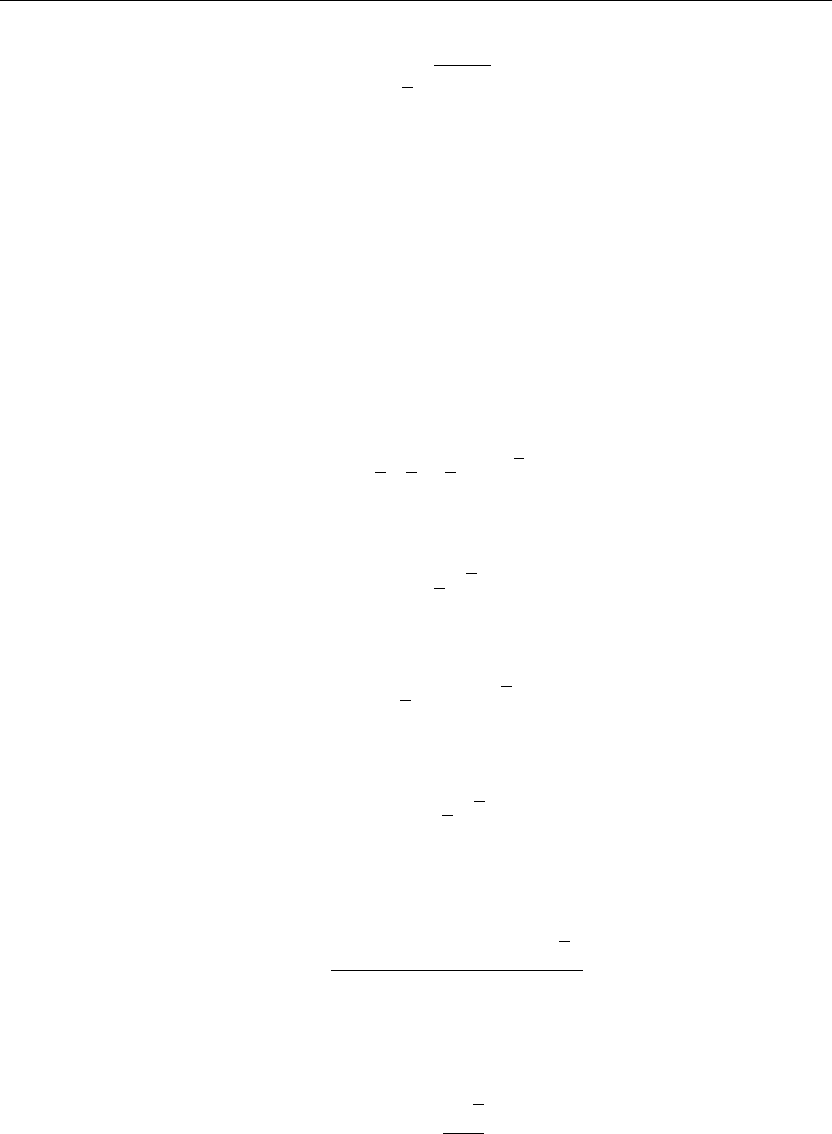
258 Chapter 4
> omega[n]:=sqrt(lambda[n]ˆ2*cˆ2−gammaˆ2/4);
ω
n
:=
1
5
λ
2
n
−1 (4.100)
From Section 4.8, the coefficients A(n) and B(n) are to be determined from the inner product
of the eigenfunctions and the initial condition functions u(r, 0) = f(r) and u
t
(r, 0) = g(r).
> f(r):=1−rˆ2;
f(r) := 1 −r
2
(4.101)
> g(r):=1−rˆ2;
g(r) := 1 −r
2
(4.102)
For n = 0,
> A(0):=Int((f(r)*gamma+g(r))/gamma*R[0](r)*w(r),r=a..b);
A(0) :=
1
0
5
2
7
5
−
7
5
r
2
√
2 r dr (4.103)
> A(0):=value(%);
A(0) :=
7
8
√
2 (4.104)
> B(0):=Int((−1/gamma)*g(r)*R[0](r)*w(r),r=a..b);
B(0) :=
1
0
−
5
2
(1 −r
2
)
√
2 r
dr (4.105)
> B(0):=value(%);
B(0) := −
5
8
√
2 (4.106)
For n = 1, 2, 3,...,
> A(n):=Int(f(r)*R[n](r)*w(r),r=a..b);
A(n) :=
1
0
(1 −r
2
) BesselJ(0,λ
n
r)
√
2 r
BesselJ(0,λ
n
)
dr (4.107)
Substitution of the eigenvalue equation simplifies the preceding equation
> A(n):=subs(BesselJ(1,lambda[n]*b)=0,value(%));
A(n) := −
2
√
2
λ
2
n
(4.108)

The Wave Partial Differential Equation 259
> B(n):=(Int((f(r)*gamma/2+g(r))*R[n](r)*w(r),r=a..b))/omega[n];
B(n) :=
5
⎛
⎝
1
0
6
5
−
6
5
r
2
BesselJ(0,λ
n
r)
√
2r
BesselJ(0,λ
n
)
dr
⎞
⎠
λ
2
n
−1
(4.109)
Substitution of the eigenvalue equation simplifies the preceding equation
> B(n):=subs(BesselJ(1,lambda[n]*b)=0,value(%));
B(n) := −
12
√
2
λ
2
n
λ
2
n
−1
(4.110)
Generalized series terms
> u[0](r,t):=simplify(eval(T[0](t)*R[0](r))):u[n](r,t):=simplify(eval(T[n](t)*R[n](r))):
Series solution
> u(r,t):=u[0](r,t)+Sum(u[n](r,t),n=1..infinity);
u(r, t) :=
7
4
−
5
4
e
−
2
5
t
(4.111)
+
∞
n=1
⎛
⎜
⎜
⎝
−
4e
−
1
5
t
BesselJ(0,λ
n
r)
cos
1
5
λ
2
n
−1 t
λ
2
n
−1 +6 sin
1
5
λ
2
n
−1 t
BesselJ
(
0,λ
n
)
λ
2
n
λ
2
n
−1
⎞
⎟
⎟
⎠
Evaluation of the eigenvalues from the roots of the eigenvalue equation yields
> BesselJ(1,lambda[n]*b)=0;
BesselJ(1,λ
n
) = 0 (4.112)
> plot(BesselJ(1,v),v=0..20,thickness=10);
If we set v = λb, then the eigenvalues are found from the intersection points of the curve with
the v-axis shown in Figure 4.9. Evaluation of a few of these eigenvalues using the Maple fsolve
command yields
> lambda[1]:=(1/b)*fsolve(BesselJ(1,v)=0,v=1..4);
λ
1
:= 3.831705970 (4.113)
260 Chapter 4
v
51520
20.3
20.2
20.1
0
0.1
0.2
0.3
0.4
0.5
10
Figure 4.9
> lambda[2]:=(1/b)*fsolve(BesselJ(1,v)=0,v=4..8);
λ
2
:= 7.015586670 (4.114)
> lambda[3]:=(1/b)*fsolve(BesselJ(1,v)=0,v=8..12);
λ
3
:= 10.17346814 (4.115)
First few terms in sum
> u(r,t):=u[0](r,t)+eval(sum(u[n](r,t),n=1..1)):
ANIMATION
> animate(u(r,t),r=a..b,t=0..5,thickness=3);
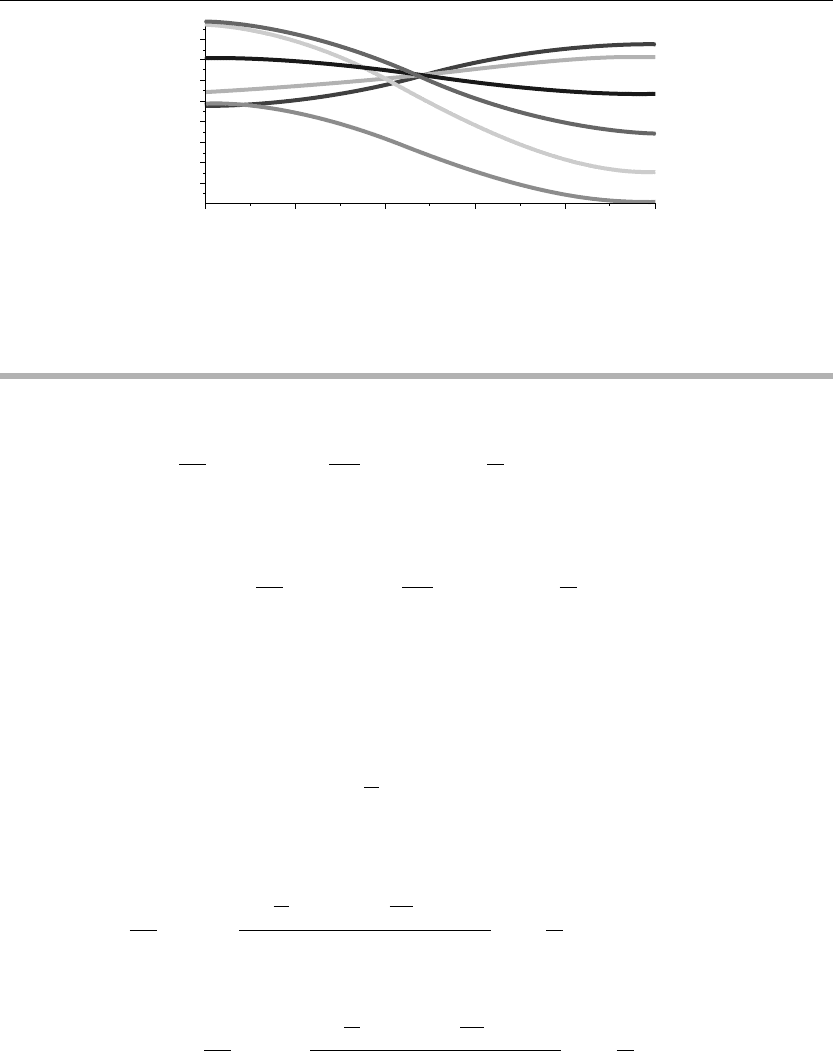
The preceding animation command illustrates the spatial-time-dependent solution for u(r, t).
The following animation sequence in Figure 4.10 shows snapshots of the animation at times
t = 0, 1, 2, 3, 4, and 5.
ANIMATION SEQUENCE
> u(r,0):=subs(t=0,u(r,t)):u(r,1):=subs(t=1,u(r,t)):
> u(r,2):=subs(t=2,u(r,t)):u(r,3):=subs(t=3,u(r,t)):
> u(r,4):=subs(t=4,u(r,t)):u(r,5):=subs(t=5,u(r,t)):
> plot({u(r,0),u(r,1),u(r,2),u(r,3),u(r,4),u(r,5)},r=a..b,thickness=10);
THREE-DIMENSIONAL ANIMATION
> u(x,y,t):=eval(subs(r=sqrt(xˆ2+yˆ2),u(r,t))):
> u(x,y,t):=u(x,y,t)*Heaviside(1−sqrt(xˆ2+yˆ2)):
> animate3d(u(x,y,t),x=−b..b,y=−b..b,t=0..10,axes=framed,thickness=1);
The Wave Partial Differential Equation 261
r
0.0 0.2 0.4 0.6 0.8 1
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Figure 4.10
Chapter Summary
Nonhomogeneous wave equation of dimension one in rectangular coordinates
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
+h(x, t)
Linear wave operator in rectangular coordinates of dimension one
L(u) =
∂
2
∂t
2
u(x, t) −c
2
∂
2
∂x
2
u(x, t)
+γ
∂
∂t
u(x, t)
Method of separation of variables solution
u(x, t) = X(x)T(t)
Eigenfunction expansion solution
u(x, t) =
∞
n=0
X
n
(x)e
−
γt
2
(
A(n) cos
(
ω
n
t
)
+B(n) sin
(
ω
n
t
))
Nonhomogeneous wave equation of dimension one in cylindrical coordinates
∂
2
∂t
2
u(r, t) =
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
−γ
∂
∂t
u(r, t)
+h(r, t)
Linear wave operator in cylindrical coordinates of dimension one
L(u) =
∂
2
∂t
2
u(r, t) −
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
+γ
∂
∂t
u(r, t)
Method of separation of variables solution
u(r, t) = R(r)T(t)

262 Chapter 4
Eigenfunction expansion solution
u(r, t) =
∞
n=0
R
n
(r)e
−
γt
2
(
A(n) cos
(
ω
n
t
)
+B(n) sin
(
ω
n
t
))
We have examined solutions to the wave partial differential equation in a single spatial
dimension for both the rectangular and the polar-cylindrical coordinate systems. We will
examine these same partial differential equations in steady-state and higher-dimensional
systems later.
Exercises
We now consider wave equations with homogeneous boundary conditions in both the
rectangular and cylindrical coordinate systems. Use the method of separation of variables and
eigenfunction expansions to evaluate the solutions to the following exercises.
Exercises in Rectangular Coordinates
4.1. Consider the transverse wave motion on a taut string over the finite interval
I ={x |0 <x<1} in a slightly damped medium. The homogeneous partial differential
equation reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/4,γ = 1/5, and boundary conditions
u(0,t)= 0 and u(1,t)= 0
The left end and the right end are held fixed. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the four sets of initial conditions
given:
f 1(x) = 1 and g1(x) = 0
f 2(x) = x and g2(x) = 1
f 3(x) = x(1 −x) and g3(x) = 0
The plucked string. For 0 <x<1/2,
f 4(x) = x and g4(x) = 0

The Wave Partial Differential Equation 263
For 1/2 <x<1,
f 4(x) = 1 −x and g4(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.2. Consider longitudinal wave motion in a bar over the finite interval I ={x |0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation
reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/5,γ = 1/5, and boundary conditions
u(0,t)= 0 and u
x
(1,t)= 0
The left end is secured and the right end is unsecured. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) =
x −
1
2
2
and g1(x) = 0
f 2(x) = x and g2(x) = 1
f 3(x) = x
1 −
x
2
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.3. Consider longitudinal wave motion in a bar over the finite interval I ={x|0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/4,γ = 1/5, and boundary conditions
u
x
(0,t)= 0 and u(1,t)= 0
The left end is unsecured and the right end is secured. The initial conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)

264 Chapter 4
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 and g2(x) = 1
f 3(x) = 1 −x
2
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.4. Consider longitudinal wave motion in a bar over the finite interval I ={x |0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/4,γ = 1/5, and boundary conditions
u
x
(0,t)= 0 and u
x
(1,t)= 0
The left end and the right end are unsecured. The initial conditions are
u(x, 0) = f(x), u
t
(x, 0) = g(x)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 −x
2
and g2(x) = 1
f 3(x) = x
2
1 −
2x
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.5. Consider longitudinal wave motion in a bar over the finite interval I ={x |0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation
reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)

The Wave Partial Differential Equation 265
with c = 1/4,γ = 1/5, and boundary conditions
u(0,t)= 0 and u
x
(1,t)+u(1,t)= 0
The left end is secured and the right end is attached to an elastic hinge. The initial
conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) = 1 and g1(x) = 0
f 2(x) = x and g2(x) = 1
f 3(x) = x
1 −
2x
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.6. Consider longitudinal wave motion in a bar over the finite interval I ={x |0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation
reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/4,γ = 1/5, and boundary conditions
u
x
(0,t)−u(0,t)= 0 and u(1,t)= 0
The left end is attached to an elastic hinge and the right end is secured. The initial
conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) = 1 and g1(x) = 0
f 2(x) = 1 −x and g2(x) = 1
f 3(x) =−
2x
2
3
+
x
3
+
1
3
and g3(x) = 0

266 Chapter 4
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.7. Consider longitudinal wave motion in a bar over the finite interval I ={x |0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation
reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/4,γ = 1/5, and boundary conditions
u
x
(0,t)= 0 and u
x
(1,t)+u(1,t)= 0
The left end is unsecured and the right end is attached to an elastic hinge. The initial
conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 and g2(x) = 1
f 3(x) = 1 −
x
2
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.8. Consider longitudinal wave motion in a bar over the finite interval I ={x |0 <x<1}
with a slight amount of damping. The homogeneous partial differential equation
reads as
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
with c = 1/4,γ = 1/5, and boundary conditions
u
x
(0,t)−u(0,t)= 0 and u
x
(1,t)= 0
The left end is attached to an elastic hinge and the right end is unsecured. The initial
conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)

The Wave Partial Differential Equation 267
Evaluate the eigenvalues and corresponding orthonormalized eigenfunctions, and write
the general solution. Evaluate the solution for each of the three sets of initial conditions
given:
f 1(x) = x and g1(x) = 0
f 2(x) = 1 and g2(x) = 1
f 3(x) = 1 −
(x −1)
2
3
and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
4.9. We consider the transverse wave motion along a taut string over the finite interval
I ={x |0 <x<1}. In addition to slight damping, the string is immersed in a medium
that provides a restoring force that is proportional to the displacement of the string
(Hooke’s law–type of force). The resulting partial differential equation is called the
“telegraph” equation:
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
−ζu(x, t)
with c = 1/4,γ = 1/5,ζ = 1/10, and boundary conditions
u(0,t)= 0 and u(1,t)= 0
The left end of the string and the right end of the string are secured. The initial
conditions are
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
Use the method of separation of variables to evaluate the eigenvalues and
corresponding orthonormalized eigenfunctions, and write the general solution. Evaluate
the solution for each of the three sets of initial conditions given:
f 1(x) = 1 and g1(x) = 0
f 2(x) = x and g2(x) = 1
f 3(x) = x(x −1) and g3(x) = 0
Generate the animated solution for each case, and plot the animated sequence for
0 <t<5.
