Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


238 Chapter 4
> A(0):=value(%);
A(0) := 0 (4.43)
> B(0):=Int((−1/gamma)*g(x)*X[0](x)*w(x),x=a..b);
B(0) :=
1
0
0dx (4.44)
> B(0):=value(%);
B(0) := 0 (4.45)
For n = 1, 2, 3,...,
> A(n):=eval(Int(f(x)*X[n](x)*w(x),x=a..b));A(n):=expand(value(%)):
A(n) :=
1
0
(4x
3
−6x
2
+1)
√
2 cos(nπx) dx (4.46)
> A(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn}, A(n)));
A(n) := −
24
√
2 (−1 +(−1)
n
)
n
4
π
4
(4.47)
> B(n):=eval(Int((f(x)*gamma/2+g(x))*X[n](x)*w(x),x=a..b)/omega[n]);
B(n):=expand(value(%)):
B(n) :=
20
1
0
2
5
x
3
−
3
5
x
2
+
1
10
√
2 cos(nπx) dx
25n
2
π
2
−4
(4.48)
> B(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},B(n)));
B(n) := −
48
√
2 (−1 +(−1)
n
)
n
4
π
4
25n
2
π
2
−4
(4.49)
Generalized series terms
> u[0](x,t):=eval(T[0](t)*X[0](x)):u[n](x,t):=eval(T[n](t)*X[n](x)):
The Wave Partial Differential Equation 239
Series solution
> u(x,t):=u[0](x,t)+Sum(u[n](x,t),n=1..infinity);
u(x, t) :=
∞
n=1
e
−
1
10
t
⎛
⎝
−
24
√
2(−1 +(−1)
n
) cos
1
20
25n
2
π
2
−4 t
n
4
π
4
(4.50)
−
48
√
2(−1 +(−1)
n
) sin
1
20
25n
2
π
2
−4 t
n
4
π
4
25n
2
π
2
−4
⎞
⎠
√
2 cos(nπx)
First few terms of sum
> u(x,t):=u[0](x,t)+sum(u[n](x,t),n=1..3):
ANIMATION
> animate(u(x,t),x=a..b,t=0..20,thickness=3);
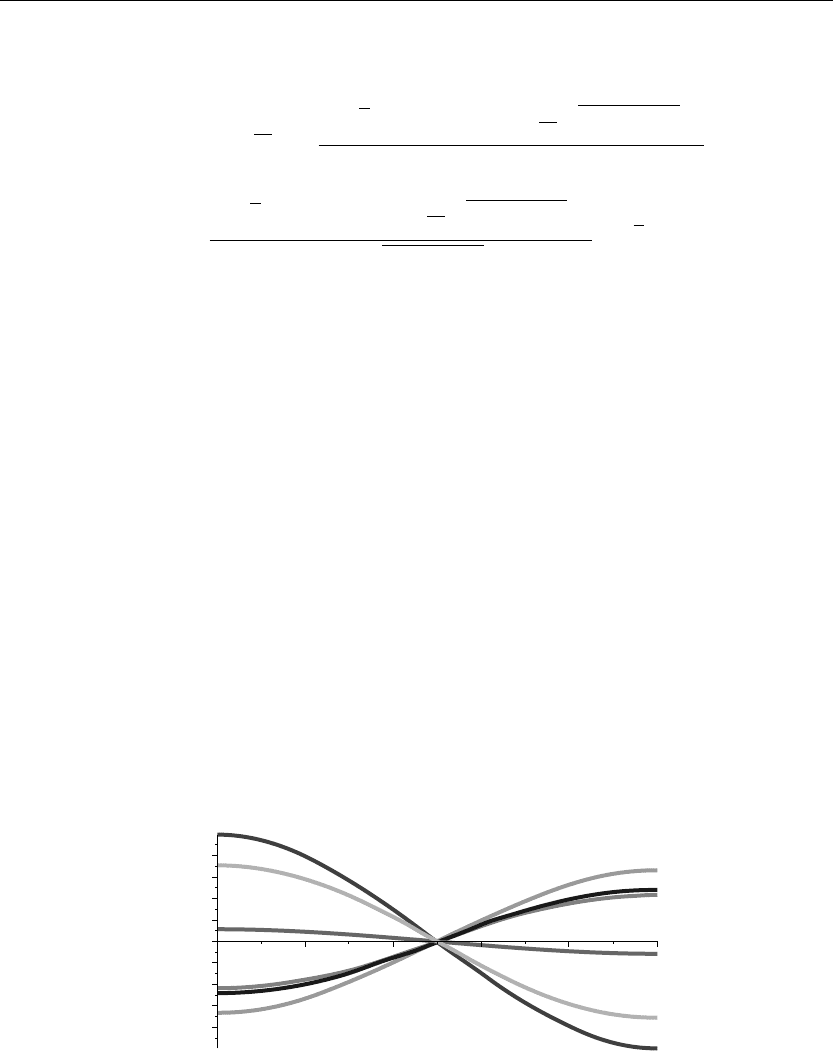
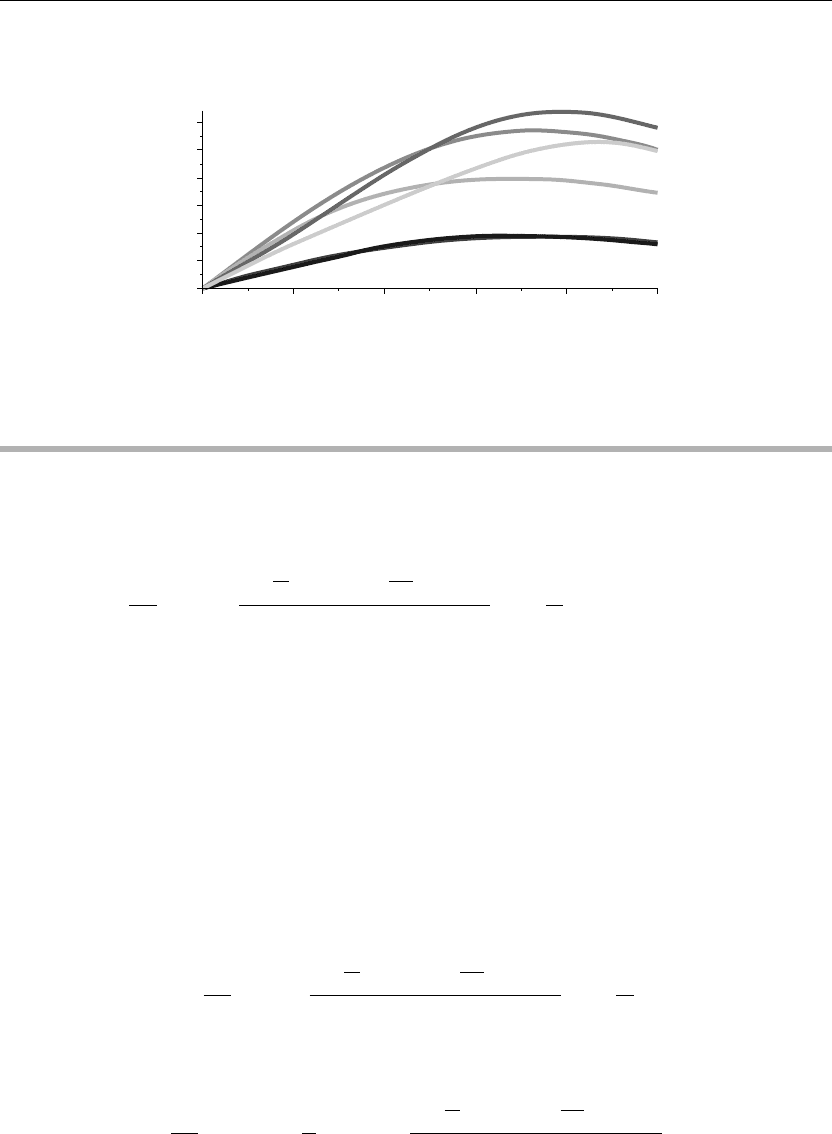
The preceding animation command illustrates the spatial-time-dependent solution for u(x, t).
Of particular note is that since the bar is initially extended symmetrically and both ends of the
bar are unsecured, the subsequent vibrations indicate a symmetric longitudinal oscillation of
the bar about its center. The following animation sequence in Figure 4.4 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, and 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=a..b,thickness=10);
x
0.2
20.8
20.6
20.4
20.2
0
0.2
0.4
0.6
0.8
0.4 0.6 0.8 1
Figure 4.4
EXAMPLE 4.6.4: We seek the wave distribution u(x, t) for longitudinal vibrations in a rigid
bar over the finite interval I ={x |0 <x<1}. The left end of the bar is secure, and the right
240 Chapter 4
end is attached to an elastic hinge. The damping is small, and the bar has an initial
displacement distribution f(x) and an initial speed distribution g(x) given as follows. The
wave speed is c = 1/4, and the damping factor is γ = 1/5.
SOLUTION: The homogeneous wave equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
The boundary conditions are type 1 at x = 0 and type 3 at x = 1
u(0,t)= 0 and u
x
(1,t)+u(1,t)= 0
The initial conditions are
u(x, 0) = x −
2x
2
3
and u
t
(x, 0) = x
The ordinary differential equations from the method of separation of variables are
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t) = 0
and
d
2
dx
2
X(x)+λX(x) = 0 (4.51)
The boundary conditions on the spatial equation are
X(0) = 0 and X
x
(1) +X(1) = 0
Assignment of system parameters
> restart:with(plots):a:=0:b:=1:c:=1/4:unprotect(gamma):gamma:=1/5:
Allowed eigenvalues and orthonormalized eigenfunctions are obtained from Example 2.5.4.
The eigenvalues are the roots of the eigenvalue equation
> tan(sqrt(lambda[n]*b))=−sqrt(lambda[n]);
tan
λ
n
=−
λ
n
(4.52)
For n = 1, 2, 3,...,
> X[n](x):=sqrt(2)*(1/sqrt((cos(sqrt(lambda[n]*b))ˆ2+b)))*sin(sqrt(lambda[n])*x);
X[m](x):=subs(n=m,X[n](x)):
X
n
(x) :=
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
(4.53)

The Wave Partial Differential Equation 241
Statement of orthonormality with respect to the weight function w(x) = 1
> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=a..b)=delta(n,m);
1
0
2 sin
√
λ
n
x
sin
√
λ
m
x
cos
√
λ
n
2
+1
cos
√
λ
m
2
+1
dx = δ(n, m) (4.54)
Time-dependent solution
> T[n](t):=exp((−gamma/2)*t)*(A(n)*cos(omega[n]*t)+B(n)*sin(omega[n]*t));
T
n
(t) := e
−
1
10
t
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t)) (4.55)
Generalized series terms
> u[n](x,t):=T[n](t)*X[n](x):
Eigenfunction expansion
> u(x,t):=Sum(u[n](x,t),n=1..infinity);
u(x, t) :=
∞
n=1
e
−
1
10
t
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t))
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
(4.56)
> omega[n]:=sqrt(lambda[n]*cˆ2−gammaˆ2/4);
ω
n
:=
1
20
25λ
n
−4 (4.57)
From Section 4.5, the coefficients A(n) and B(n) are to be determined from the inner
product of the eigenfunctions and the initial condition functions u(x, 0) = f(x) and
u
t
(x, 0) = g(x).
> f(x):=x−2/3*xˆ2;
f(x) := x −
2
3
x
2
(4.58)
> g(x):=x;
g(x) := x (4.59)
For n = 1, 2, 3,...,
> A(n):=eval(Int(f(x)*X[n](x)*w(x),x=a..b));A(n):=expand(value(%)):
A(n) :=
1
0
x −
2
3
x
2
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
dx (4.60)
242 Chapter 4
Substitution of the eigenvalue equation simplifies the preceding equation
> A(n):=simplify(subs(sin(sqrt(lambda[n])*b)=−sqrt(lambda[n])*cos(sqrt(lambda[n])*b),
A(n)));
A(n) := −
4
3
√
2
−1 +cos
√
λ
n
λ
(3/2)
n
cos
√
λ
n
2
+1
(4.61)
> B(n):=eval(Int((f(x)*gamma/2+g(x))*X[n](x)*w(x),x=a..b)/omega[n]);
B(n):=expand(value(%)):
B(n) :=
20
⎛
⎜
⎝
1
0
11
10
x −
1
15
x
2
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
dx
⎞
⎟
⎠
√
25λ
n
−4
(4.62)
Substitution of the eigenvalue equation simplifies this equation
> B(n):=simplify(subs(sin(sqrt(lambda[n])*b)=−sqrt(lambda[n])*cos(sqrt(lambda[n])*b),
B(n)));
B(n) := −
8
3
√
2
−1 +15 cos
√
λ
n
λ
n
+cos
√
λ
n
λ
(3/2)
n
cos
√
λ
n
2
+1
√
25λ
n
−4
(4.63)
Generalized series terms
> u[n](x,t):=eval(T[n](t)*X[n](x)):
Series solution
> u(x,t):=Sum(u[n](x,t),n=1..infinity);
u(x, t) :=
∞
n=1
1
cos
√
λ
n
2
+1
⎛
⎜
⎝
e
−
1
10
t
⎛
⎜
⎝
−
4
3
√
2
−1 +cos
√
λ
n
cos
1
20
√
25λ
n
−4 t
λ
(3/2)
n
cos
√
λ
n
2
+1
(4.64)
−
8
3
√
2
−1 +15 cos
√
λ
n
λ
n
+cos
√
λ
n
sin
1
20
√
25λ
n
−4 t
λ
(3/2)
n
cos
√
λ
n
2
+1
√
25λ
n
−4
⎞
⎟
⎠
√
2 sin
λ
n
x
⎞
⎟
⎠
Evaluation of the eigenvalues from the roots of the eigenvalue equation yields
> tan(sqrt(lambda[n])*b)=−sqrt(lambda[n]);
tan
λ
n
=−
λ
n
(4.65)
The Wave Partial Differential Equation 243
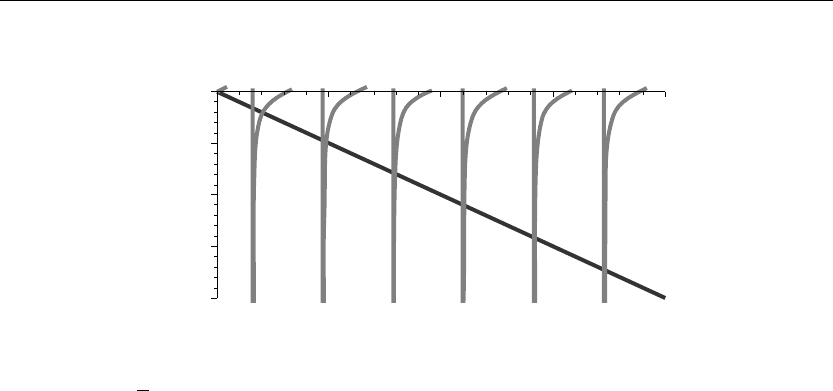
> plot({tan(v),−v},v=0..20,y=−20..0,thickness=10);
10
v
20
220
215
210
25
0
515
y
Figure 4.5
If we set v =
√
λb, then the eigenvalues are determined from the squares of the values of v at
the intersection points of the curves in Figure 4.5. Evaluation of the first few eigenvalues using
the Maple fsolve command yields:
> lambda[1]:=(1/bˆ2)*(fsolve((tan(v)+v),v=1..3)ˆ2);
λ
1
:= 4.115858365 (4.66)
> lambda[2]:=(1/bˆ2)*(fsolve((tan(v)+v),v=3..6)ˆ2);
λ
2
:= 24.13934203 (4.67)
> lambda[3]:=(l/bˆ2)*(fsolve((tan(v)+v),v=6..9)ˆ2);
λ
3
:= 63.65910654 (4.68)
First few terms of sum
> u(x,t):=eval(sum(u[n](x,t),n=1..3)):
ANIMATION
> animate(u(x,t),x=a..b,t=0..20,thickness=3);
The preceding animation command illustrates the spatial-time-dependent solution for u(x, t).
The following animation sequence in Figure 4.6 shows snapshots of the animation at times
t = 0, 1, 2, 3, 4, and 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
244 Chapter 4
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=a..b,thickness=10);
x
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
1.2
Figure 4.6
4.7 Wave Equation in the Cylindrical Coordinate System
The partial differential equation for wave phenomena in the cylindrical coordinate system for
a circularly symmetric system is given below. Here, u(r, t) is the spatial-time-dependent
solution
∂
2
∂t
2
u(r, t) =
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
−γ
∂
∂t
u(r, t)
+h(r, t)
and r is the coordinate radius of the system. See the references for the equivalency of the
wave equation from the rectangular cartesian system to the cylindrical coordinate system.
There is no angle dependence here because we have assumed circular symmetry, and there is
no z dependence because we will be considering regions with no extension along the z-axis.
As for the rectangular coordinate system, we can write the preceding in terms of the linear
operator for the wave equation in cylindrical coordinates as
L(u) = h(r, t)
where the wave operator in cylindrical coordinates reads as
L(u) =
∂
2
∂t
2
u(r, t) −
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
+γ
∂
∂t
u(r, t)
We now consider the homogeneous version of the partial differential equation:
∂
2
∂t
2
u(r, t) +γ
∂
∂t
u(r, t)
=
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r
The Wave Partial Differential Equation 245
We seek solutions to this partial differential equation over the finite interval I ={r |a<r<b}
subject to the nonregular homogeneous boundary conditions
|u(a, t)| < ∞
and
κ
1
u(b, t) +κ
2
u
r
(b, t) = 0
with the initial conditions
u(r, 0) = f(r)
and
u
t
(r, 0) = g(r)
Similar to the procedure for rectangular coordinates, we solve the partial differential equation
using the method of separation of variables. We set
u(r, t) = R(r)T(t)
Substituting this into the preceding homogeneous partial differential equation yields
R(r)
d
2
dt
2
T(t) +γ
d
dt
T(t)
=
c
2
T(t)
d
dr
R(r) +r
d
2
dr
2
R(r)
r
Dividing both sides by the product solution, we get
d
2
dt
2
T(t) +γ
d
dt
T(t)
c
2
T(t)
=
d
dr
R(r) +r
d
2
dr
2
R(r)
R(r)r
Because the left-hand side of this equation is an exclusive function of t and the right-hand side
an exclusive function of r, and t and r are independent, then the only way we can ensure
equality of the preceding for all r and t is to set each side equal to a constant.
Doing so, we arrive at the following two ordinary differential equations in terms of the
separation constant λ
2
:
d
2
dt
2
T(t) +γ
∂
∂t
T(r, t)
+λ
2
c
2
T(t) = 0
and
d
2
dr
2
R(r) +
d
dr
R(r)
r
+λ
2
R(r) = 0
The preceding differential equation in t is an ordinary second-order linear differential equation
for which we already have the solution from Chapter 1.

246 Chapter 4
The second differential equation in the variable r is recognized from Section 1.11 as being an
ordinary Bessel differential equation. The solution of this equation is the Bessel function of the
first kind of order zero.
We noted in Section 2.6 that, for the Bessel differential equation, the point r = 0 is a regular
singular point of the differential equation. With appropriate boundary conditions over an
interval that includes the origin, we arrive at a “nonregular” (singular) type Sturm-Liouville
eigenvalue problem whose eigenfunctions form an orthogonal set.
Similar to regular Sturm-Liouville problems over finite intervals, an infinite number of
eigenvalues exist that can be indexed by the positive integers n. The indexed eigenvalues and
corresponding eigenfunctions are given, respectively, as
λ
n
,R
n
(r)
for n = 0, 1, 2, 3,....
The eigenfunctions form a “complete” set with respect to any piecewise smooth function over
the finite interval I ={r |a<r<b}. In Section 2.6, we examined the nature of the
orthogonality of the Bessel functions, and we showed the eigenfunctions to be orthogonal with
respect to the weight function w(r) = r over the finite interval I. Further, the eigenfunctions
can be normalized, and the corresponding statement of orthonormality reads
b
a
R
n
(r)R
m
(r)r dr =δ(n, m)
where the term on the right is the familiar Kronecker delta function.
Using arguments similar to that used for the regular Sturm-Liouville problem, we can write
our general solution to the partial differential equation as the superposition of the products of
the solutions to each of the ordinary differential equations given earlier.
We now consider the time-dependent differential equation, which reads
d
2
dt
2
T(t) +γ
∂
∂t
T(r, t)
+λ
2
c
2
T(t) = 0
For the indexed values of λ, the solution to this equation is
T
n
(t) = e
−
γt
2
(
A(n) cos
(
ω
n
t
)
+B(n) sin
(
ω
n
t
))
where the n-th term damped angular frequency ω
n
is given in terms of the indexed λ
n
as
ω
n
=
4λ
2
n
c
2
−γ
2
2

The Wave Partial Differential Equation 247
for n = 0, 1, 2, 3,.... In the preceding equation, the coefficients A(n) and B(n) are unknown
arbitrary constants and we have assumed small damping in the system—that is,
γ
2
< 4λ
2
n
c
2
Thus, by the method of separation of variables, we arrive at an infinite number of indexed
solutions u
n
(r,t)(n= 0, 1, 2, 3,...) for the homogeneous wave partial differential equation,
over a finite interval, given as
u
n
(r, t) = R
n
(r)e
−
γt
2
(
A(n) cos
(
ω
n
t
)
+B(n) sin
(
ω
n
t
))
Because the differential operator is linear, then any superposition of solutions to the
homogeneous equation is also a solution to the problem. Thus, we can write the general
solution to the homogeneous partial differential equation as the infinite sum
u(r, t) =
∞
n=0
R
n
(r)e
−
γt
2
(
A(n) cos
(
ω
n
t
)
+B(n) sin
(
ω
n
t
))
We demonstrate the preceding concepts with an example wave problem in cylindrical
coordinates.
DEMONSTRATION: We seek the wave distribution u(r, t) for transverse vibrations in a
thin circularly symmetric membrane over the interval I ={r |0 <r<1}, which is secure
at the periphery. The membrane vibrates in a medium with a small amount of damping.
The membrane has an initial displacement distribution f(r) and an initial speed distribution
g(r) given as follows. The wave speed is c = 1/5, and the damping factor is γ = 2/5.
SOLUTION: The homogeneous wave equation is
∂
2
∂t
2
u(r, t) +
2
∂
∂t
u(r, t)
5
=
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
25r
The boundary conditions are type 1 at r = 1, and we require a finite solution at the origin
|u(0,t)| < ∞ and u(1,t)= 0
The initial conditions are
u(r, 0) = f(r) and u
t
(r, 0) = g(r)
From the method of separation of variables, the ordinary differential equations are
d
2
dt
2
T(t) +
2
d
dt
T(t)
5
+
λ
2
T(t)
25
= 0
