Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


218 Chapter 4
We can write the preceding nonhomogeneous equation in terms of the linear wave operator as
L(u) = h(x, t)
where the wave operator in rectangular coordinates is
L(u) =
∂
2
∂t
2
u(x, t) −c
2
∂
2
∂x
2
u(x, t)
+γ
∂
∂t
u(x, t)
If h(x, t) = 0, then there are no external applied forces acting on the system, and the preceding
nonhomogeneous partial differential equation reduces to the corresponding homogeneous
equation
L(u) = 0
For the case of no source terms and no damping in the system, the wave equation can be
written in the more familiar form
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
This partial differential equation for wave phenomena is characterized by the fact that it relates
the second partial derivative with respect to the time variable with the second partial derivative
with respect to the spatial variable.
Similar to what we did for the diffusion equation, some motivation for the derivation of the
wave equation can be provided in terms of some simple concepts from introductory calculus.
Recall that the slope of a curve of a function is found from the first derivative, and the
concavity of the curve is found from the second derivative with respect to the spatial variable x.
In addition, the speed or time rate of change of a function is given as the first derivative, and its
acceleration is given as the second derivative with respect to the time variable t.
We imagine the sideview profile of a taut string that is secured at both end points. We assume
small-amplitude vibrations of the string so the tension can be assumed to be invariant with
respect to time and position along the string. At those points along the string where the profile
is most bent, as indicated by large values of concavity, we expect the string to want to resist
further bending and to provide a large return force. From Newton’s second law, large forces
provide large accelerations; thus, at regions of large concavity, the string should experience
large return accelerations. For a string whose local profile is concave down, we expect a
negative return acceleration, which forces the string back to its unstretched position. Thus, the
acceleration of the local profile is proportional to the spatial concavity of the profile: the exact
behavior as described by the preceding partial differential equation.
A typical example wave problem follows. We consider the waves describing the longitudinal
vibrations in a rigid bar over the finite interval I ={x |0 <x<1}. The left end of the bar is
secure, and the right end is attached to an elastic hinge. The wave speed is c, and the damping

The Wave Partial Differential Equation 219
term γ is very small. The initial displacement distribution is f(x), and the initial speed
distribution is g(x).
The partial differential equation that describes the wave distribution u(x, t) for longitudinal
vibrations in the bar is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
Since the bar is secured at the left end and hinged at the right end, the boundary conditions are
of type 1 at x = 0 and type 3 at x = 1.
u(0,t)= 0
and
u
x
(1,t)+u(1,t)= 0
The initial displacement condition on the bar is
u(x, 0) = f(x)
and the initial speed distribution is
u
t
(x, 0) = g(x)
We solve this particular problem later. For now, we develop generalized procedures for the
solution to this homogeneous partial differential equation over a finite domain with
homogeneous boundary conditions using the method of separation of variables.
4.3 Method of Separation of Variables for the
Wave Equation
The homogeneous wave equation for a uniform system in one dimension in rectangular
coordinates can be written as
∂
2
∂t
2
u(x, t) −c
2
∂
2
∂x
2
u(x, t)
+γ
∂
∂t
u(x, t)
= 0
This can be rewritten in the more familiar form as
∂
2
∂t
2
u(x, t) +γ
∂
∂t
u(x, t)
= c
2
∂
2
∂x
2
u(x, t)
Generally, one seeks a solution to this problem over the finite one-dimensional domain
I ={x |a<x<b}, subject to the regular homogeneous boundary conditions
κ
1
u(a, t) +κ
2
u
x
(a, t) = 0

220 Chapter 4
and
κ
3
u(b, t) +κ
4
u
x
(b, t) = 0
and the two initial conditions
u(x, 0) = f(x)
and
u
t
(x, 0) = g(x)
Here, f(x) denotes the initial displacement of the wave, and g(x) denotes the initial speed of
the amplitude of the wave.
In the method of separation of variables, the character of the equation is such that we can
assume a solution in the form of a product as follows:
u(x, t) = X(x)T(t)
As in the case of the diffusion equation, because the two independent variables in the partial
differential equation are the spatial variable x and the time variable t, then the preceding
assumed solution is written as a product of two functions; one is exclusively a function of x
and the other an exclusive function of t.
Substituting this assumed solution into the partial differential equation yields
X(x)
d
2
dt
2
T(t)
+γX(x)
d
dt
T(t)
= c
2
d
2
dx
2
X(x)
T(t)
Dividing both sides of the preceding equation by the product solution gives us
d
2
dt
2
T(t) +γ
d
dt
T(t)
c
2
T(t)
=
d
2
dx
2
X(x)
X(x)
Since the left-hand side of the preceding is an exclusive function of t and the right-hand side an
exclusive function of x, and t and x are independent, then the only way the preceding can hold
for all values of t and x is to set each side equal to a constant. Doing so, we get the following
two ordinary differential equations in terms of the separation constant λ:
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t)= 0
and
d
2
dx
2
X(x)+λX(x) = 0

The Wave Partial Differential Equation 221
This differential equation in t is an ordinary second-order linear homogeneous differential
equation for which we already have the solution from Section 1.4. Similarly, the second
differential equation in x is also an ordinary second-order linear homogeneous differential
equation for which we already have the solution from Section 1.4. We easily recognize this
differential equation as being of the Sturm-Liouville type.
4.4 Sturm-Liouville Problem for the Wave Equation
The second differential equation in the spatial variable x in the last section must be solved
subject to the homogeneous spatial boundary conditions over the finite interval. The
Sturm-Liouville problem for the wave equation consists of the ordinary differential equation
d
2
dx
2
X(x)+λX(x) = 0
along with the corresponding homogeneous boundary conditions
κ
1
X(a)+κ
2
X
x
(a) = 0
and
κ
3
X(b)+κ
4
X
x
(b) = 0
We see the preceding problem in the spatial variable x to be a regular Sturm-Liouville
eigenvalue problem where the allowed values of λ are called the system “eigenvalues” and the
corresponding solutions are called the “eigenfunctions.” Note that the ordinary differential
equation is of the Euler type and the weight function w(x) = 1.
It can be shown that for regular Sturm-Liouville problems over finite domains, an infinite
number of eigenvalues exist that can be indexed by the integers n. The indexed eigenvalues
and corresponding eigenfunctions are given, respectively, as
λ
n
,X
n
(x)
for n = 0, 1, 2, 3,....
The eigenfunctions form a “complete” set with respect to any piecewise smooth function over
the finite interval I ={x |a<x<b}. Further, the eigenfunctions can be normalized and the
corresponding statement of orthonormality reads
b
a
X
n
(x)X
m
(x) dx = δ(n, m)
where the term on the right is the familiar Kronecker delta function defined in Section 2.2.
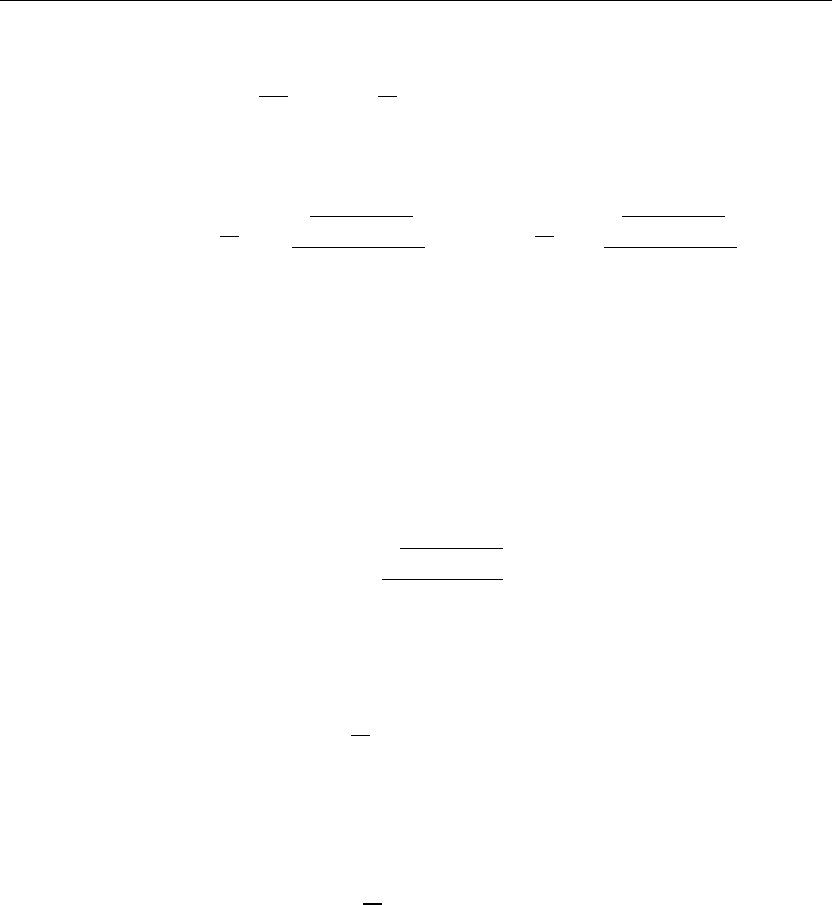
222 Chapter 4
We now consider the time-dependent differential equation, which reads
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t) = 0
From Section 1.4 on second-order linear differential equations, the solution to the preceding
time-dependent differential equation in terms of the allowed eigenvalues is
T
n
(t) = A(n)e
−
γt
2
cos
4 λ
n
c
2
−γ
2
t
2
+B(n)e
−
γt
2
sin
4 λ
n
c
2
−γ
2
t
2
The coefficients A(n) and B(n) are unknown arbitrary constants. Throughout most of our
example problems, we make the assumption that the damping in the system is small—that is,
γ
2
< 4 λ
n
c
2
This assumption gives rise to time-dependent solutions that are oscillatory. The argument of
the preceding sinusoidal sine and cosine expressions denotes ω
n
, which is the damped angular
frequency of oscillation of the n-th term in the system. The damped angular frequency of
oscillation of the n-th term or mode is
ω
n
=
4 λ
n
c
2
−γ
2
2
Thus, by the method of separation of variables, we arrive at an infinite number of indexed
solutions u
n
(x,t)(n= 0, 1, 2, 3,...) for the homogeneous wave partial differential equation,
over a finite interval, given as
u
n
(x, t) = X
n
(x)e
−
γt
2
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t))
Because the differential operator is linear, any superposition of solutions to the homogeneous
equation is also a solution to the problem. Thus, we can write the general solution to the
homogeneous partial differential equation as the infinite sum
u(x, t) =
∞
n=0
X
n
(x)e
−
γt
2
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t))
This equation is the eigenfunction expansion form of the solution to the wave partial differential
equation. The terms of the preceding sum form the “basis vectors” of the solution space of the
partial differential equation. Thus, for the wave partial differential equation, there are an
infinite number of basis vectors in the solution space, and we say the dimension of the solution
space is infinite. This compares dramatically with an ordinary differential equation where the
dimension of the solution space is finite and equal to the order of the equation. We demonstrate
the preceding concepts with the solution of an illustrative problem given earlier in Section 4.2.

The Wave Partial Differential Equation 223
DEMONSTRATION: We seek the wave distribution u(x, t) for the longitudinal vibrations in
a rigid bar over the finite interval I ={x |0 <x<1}. The left end of the bar is secure, and the
right end is attached to an elastic hinge. The wave speed is c and the damping term γ is very
small. The initial displacement distribution is f(x), and the initial speed distribution is g(x).
SOLUTION: The partial differential equation that describes the longitudinal vibrations in the
bar is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
−γ
∂
∂t
u(x, t)
Since the bar is secured at the left end and hinged at the right end, the boundary conditions are
of type 1 at x = 0 and type 3 at x = 1.
u(0,t)= 0
and
u
x
(1,t)+u(1,t)= 0
The initial conditions on the bar are
u(x, 0) = f(x)
and
u
t
(x, 0) = g(x)
From the method of separation of variables, we get the two ordinary differential equations
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t) = 0
and
d
2
dx
2
X(x)+λX(x) = 0
We consider the solution to the spatial equation first. Again, the reason for this is that the
spatial differential equation and the spatial boundary conditions determine the system
eigenvalues, and these eigenvalues must be determined before we consider the solution to the
time-dependent differential equation. Here, we have an Euler-type differential equation with a
type 1 condition at the left and a type 3 condition at the right—that is,
X(0) = 0
and
X
x
(1) +X(1) = 0
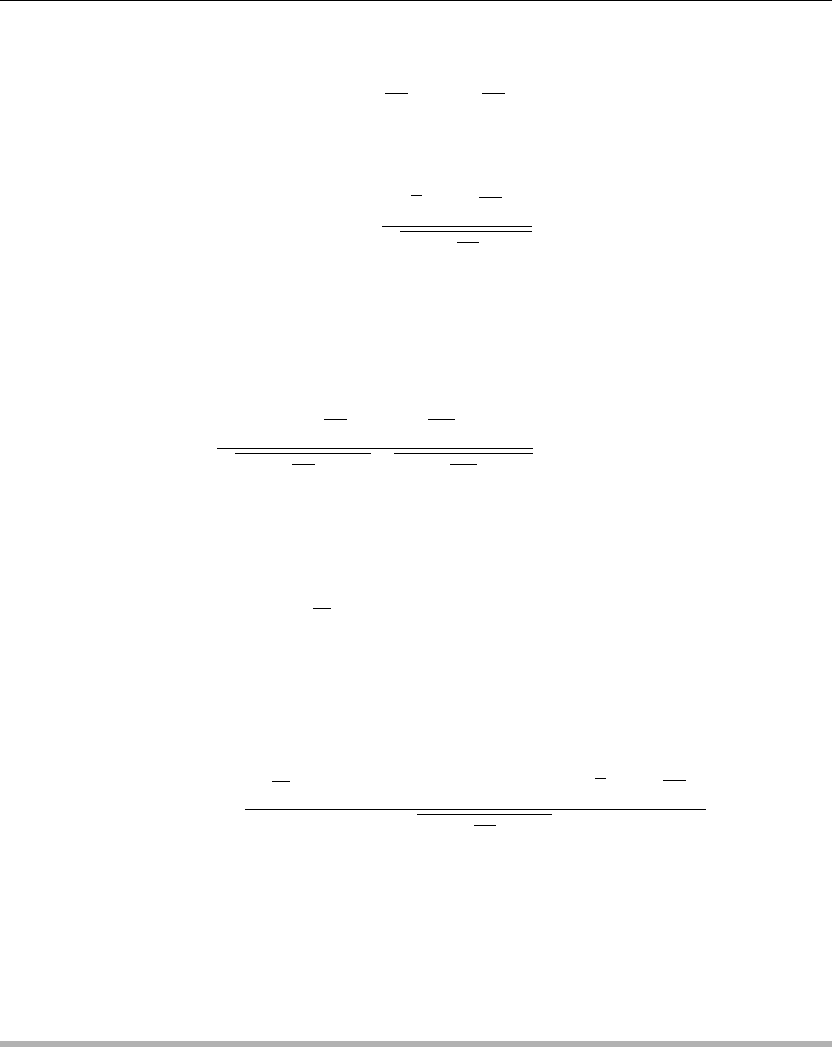
224 Chapter 4
We previously solved this problem in Example 2.5.4 in Chapter 2. The allowed eigenvalues are
the roots of the eigenvalue equation
tan
λ
n
=−
λ
n
and the corresponding orthonormalized eigenfunctions are
X
n
(x) =
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
for n = 1, 2, 3,....
The statement of orthonormality for the spatial eigenfunctions, with respect to the weight
function w(x) = 1, is
1
0
2
sin
√
λ
n
x
sin
√
λ
m
x
cos
√
λ
n
2
+1
cos
√
λ
m
2
+1
dx = δ(n, m)
for n, m = 1, 2, 3,....
The corresponding solution for the time-dependent differential equation is
T
n
(t) = e
−
γt
2
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t))
for n = 1, 2, 3,....
The final eigenfunction expansion solution to the problem is constructed from the superposition
of the products of the preceding spatial and time-dependent solutions, and this reads
u(x, t) =
∞
n=1
e
−
γt
2
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t))
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
The unknown coefficients A(n) and B(n) are to be determined from the initial conditions given
in the problem.
4.5 Initial Conditions for the Wave Equation in
Rectangular Coordinates
We now consider the initial conditions on the problem. At time t = 0, we have the initial
displacement
u(x, 0) = f(x)

The Wave Partial Differential Equation 225
and the initial amplitude speed
u
t
(x, 0) = g(x)
Substituting the first condition into the general solution
u(x, t) =
∞
n=0
X
n
(x)e
−
γt
2
(A(n) cos(ω
n
t) +B(n) sin(ω
n
t))
at time t = 0 yields
f(x) =
∞
n=0
X
n
(x)A(n)
Substituting the second condition into the time derivative of the general solution at time t = 0
yields
g(x) =
∞
n=0
X
n
(x)
ω
n
B(n) −
A(n)γ
2
Recall that the eigenfunctions of the regular Sturm-Liouville problem form a complete set with
respect to piecewise smooth functions over the finite interval I ={x |a<x<b}. Thus, both of
the preceding equations are the generalized Fourier series expansions of the functions f(x) and
g(x), respectively, in terms of the spatial eigenfunctions of the system. The terms A(n) and
B(n) are the corresponding Fourier coefficients. We now evaluate these coefficients.
As we did in Section 2.3 for the generalized Fourier series expansion, we take the inner product
of both sides of the preceding equations, with respect to the weight function w(x) = 1.
Operating on the first equation, we get
b
a
f(x)X
m
(x) dx =
∞
n=0
A(n)
⎛
⎝
b
a
X
m
(x)X
n
(x)dx
⎞
⎠
From the statement of orthonormality, this reduces to
b
a
f(x)X
m
(x) dx =
∞
n=0
A(n)δ(n, m)
From the definition of the Kronecker delta function, only one term (n = m) survives in the
sum, and we are able to extract the value
A(m) =
b
a
f(x)X
m
(x) dx

226 Chapter 4
In a similar manner, operating on the second equation and taking the inner product of both
sides, we get
b
a
g(x)X
m
(x) dx =
∞
n=0
ω
n
B(n) −
A(n)γ
2
⎛
⎝
b
a
X
m
(x)X
n
(x) dx
⎞
⎠
Again, taking advantage of the statement of orthonormality, the preceding equation reduces to
b
a
g(x)X
m
(x) dx =
∞
n=0
ω
n
B(n) −
A(n)γ
2
δ(n, m)
Evaluating the sum (only the n = m term survives) and inserting the known value for A(m)
yields
B(m) =
b
a
f(x)γ
2
+g(x)
X
m
(x) dx
ω
m
Thus, we can write the final generalized solution to the wave equation in one dimension,
subject to the earlier homogeneous boundary conditions and initial conditions, as
u(x, t) =
∞
n=0
X
n
(x)e
−
γt
2
⎛
⎜
⎜
⎜
⎝
b
a
f(x)X
n
(x) dx
cos
(
ω
n
t
)
+
b
a
f(x)γ
2
+g(x)
X
n
(x) dx
sin
(
w
n
t
)
ω
n
⎞
⎟
⎟
⎟
⎠
All of the operations given are based on the assumption that the infinite series is uniformly
convergent and the formal interchange between the operator and the summation is legitimate.
It can be shown that if the functions f(x) and g(x) satisfy the same boundary conditions as the
eigenfunctions, then both of the preceding series are uniformly convergent. We demonstrate
the evaluation of the coefficients A(n) and B(n) for the illustrative problem in Section 4.4.
DEMONSTRATION: Consider the case where the wave speed c = 1/4 and the damping
factor γ = 1/5. The initial displacement distribution is
f(x) = x −
2 x
2
3
and the initial speed distribution is
g(x) = x

The Wave Partial Differential Equation 227
SOLUTION: The calculated value of ω
n
is
ω
n
=
√
25 λ
n
−4
20
To evaluate A(n) and B(n), we take the inner products of the initial condition functions f(x)
and g(x), over the interval I ={x |0 <x<1}, with the corresponding eigenfunctions. Doing
so, we get
A(n) =
1
0
−
2 x
2
3
+x
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
dx
which evaluates to
A(n) =−
4
√
2
cos
√
λ
n
−1
3λ
3
2
n
cos
√
λ
n
2
+1
and
B(n) =
1
0
−
x
2
15
+
11x
10
√
2 sin
√
λ
n
x
cos
√
λ
n
2
+1
dx
ω
n
which evaluates to
B(n) =−
8
√
2
15 cos
√
λ
n
λ
n
+cos
√
λ
n
−1
3
√
25 λ
n
−4 λ
3
2
n
cos
√
λ
n
2
+1
for n = 1, 2, 3,....
For λ>0, the eigenvalues λ
n
are determined from the roots of the eigenvalue equation
tan
λ
n
=−
λ
n
(4.1)
Figure 4.1 shows curves of the two functions tan(v) and −v plotted on the same set of axes. If
we set v =
√
λ, then the eigenvalues are the squares of the values of v at the intersection points
of these curves.
The first three eigenvalues are
λ
1
= 4.115858365
λ
2
= 24.13934203
λ
3
= 63.65910654
