Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

288 Chapter 5

The boundary conditions are

u(0,y)= y(1 −y) and u(1,y)= 0

and

(x, 0) = 0 and u

(x, 1) = 0

Here, we see that the boundary conditions are homogeneous with respect to the y variable.

Ordinary differential equations from the method of separation of variables are

X(x)−λX(x) = 0

and

Y(y) +λY(y) = 0

Homogeneous boundary conditions on the y equation are type 2 at y = 0 and type 2 at y = 1

(0) = 0 and Y

(1) = 0

Assignment of system parameters

> restart:with(plots):a:=1:b:=1:

Allowed eigenvalues and corresponding orthonormal eigenfunctions for the y equation are

obtained from Example 2.5.3. For n = 0,

> lambda[0]:=0;

:= 0 (5.19)

Orthonormal eigenfunction

> Y[0](y):=1/sqrt(b);

(y) := 1 (5.20)

For n = 1, 2, 3,...,

> lambda[n]:=(n*Pi/b)ˆ2;

:= n

(5.21)

Orthonormal eigenfunctions

> Y[n](y):=sqrt(2/b)*cos(n*Pi/b*y);Y[n](s):=subs(y=s,Y[n](y)):Y[m](y):=subs(n=m,Y[n](y)):

(y) :=

√

2 cos(nπy) (5.22)

The Laplace Par tial Differential Equation 289

Statement of orthonormality with respect to the weight function w(y) = 1

> w(y):=1:Int(Y[n](y)*Y[m](y)*w(y),y=0..b)=delta(n,m);



2 cos(nπy) cos(mπy) dy = δ(n, m) (5.23)

Basis vectors for the x equation

> x1(x):=sinh(sqrt(lambda)*(a−x));x2(x):=cosh(sqrt(lambda)*(a−x));

x1(x) := sinh



√

λ(1 −x)



x2(x) := cosh



√

λ(1 −x)



(5.24)

General solution to the x equation for n = 1, 2, 3,...

> X[n](x):=A(n)*cosh(n*Pi/b*(a−x))+B(n)*sinh(n*Pi/b*(a−x));

(x) := A(n) cosh(nπ(1 −x)) +B(n) sinh(nπ(1 −x)) (5.25)

Substituting into the x-dependent boundary condition yields

> eval(subs(x=a,X[n](x)))=0;

A(n) = 0 (5.26)

For n = 1, 2, 3,..., we have for the x-dependent solution

> X[n](x):=B(n)*sinh(n*Pi/b*(a−x));

(x) := B(n) sinh(nπ(1 −x)) (5.27)

Similarly, for n = 0, the x-dependent solution is

> X[0](x):=B(0)*(a−x);

(x) := B(0)(1 −x) (5.28)

Generalized series terms

> u[0](x,y):=X[0](x)*Y[0](y);u[n](x,y):=X[n](x)*Y[n](y);

(x, y) := B(0)(1 −x)

(x, y) := B(n) sinh(nπ(1 −x))

√

2 cos(nπy) (5.29)

290 Chapter 5

Eigenfunction expansion

> u(x,y):=u[0](x,y)+Sum(u[n](x,y),n=1..inﬁnity);

u(x, y) := B(0)(1 −x) +

∞



n=1

B(n) sinh(nπ(1 −x))

√

2 cos(nπy) (5.30)

Evaluation of Fourier coefﬁcients from the speciﬁc remaining boundary condition

u(0,y)= f(y)

> f(y):=y*(1−y);

f(y) := y(1 −y) (5.31)

Substituting this condition into the preceding solution yields

> f(y)=subs(x=0,u(x,y));

y(1 −y) = B(0) +

∞



n=1

B(n) sinh(nπ)

√

2 cos(nπy) (5.32)

This equation is the Fourier series expansion of f(y) in terms of the orthonormal

Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier cofﬁcients, we take the

inner product of both sides with respect to the orthonormal eigenfunctions, and, taking

advantage of the previous statement of orthonormality, we get

> B(n):=(1/sinh(n*Pi*a/b))*Int(f(y)*Y[n](y)*w(y),y=0..b);B(n):=expand(value(%)):

B(n) :=



y(1 −y)

√

2 cos(nπy) dy

sinh(nπ)

(5.33)

> B(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},B(n)));

B(n) := −

√

2(1 +(−1)

)

sinh(nπ)n

(5.34)

for n = 1, 2, 3,.... Similarly, for n = 0, we get

> B(0):=eval((1/a)*Int(f(y)*Y[0](y)*w(y),y=0..b));B(0):=value(%):

B(0) :=



y(1 −y) dy (5.35)

> B(0):=subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},B(0));

B(0) :=

(5.36)

The Laplace Par tial Differential Equation 291

Generalized series terms

> u[0](x,y):=eval(X[0](x)*Y[0](y));u[n](x,y):=eval(X[n](x)*Y[n](y));

(x, y) :=

−

(x, y) := −

2(1 +(−1)

) sinh(nπ(1 −x)) cos(nπy)

sinh(nπ)n

(5.37)

Series solution

> u(x,y):=u[0](x,y)+Sum(u[n](x,y),n=1..inﬁnity);

u(x, y) :=

−

x +

∞



n=1



−

2(1 +(−1)

) sinh(nπ(1 −x)) cos(nπy)

sinh(nπ)n



(5.38)

First few terms of expansion

> u(x,y):=sum(u[0](x,y)+u[n](x,y),n=1..5):

> plot3d(u(x,y),x=0..a,y=0..b,axes=framed,thickness=1);

0.8

0.6

0.4

0.2

0.4

0.6

0.8

0.6

0.4

0.2

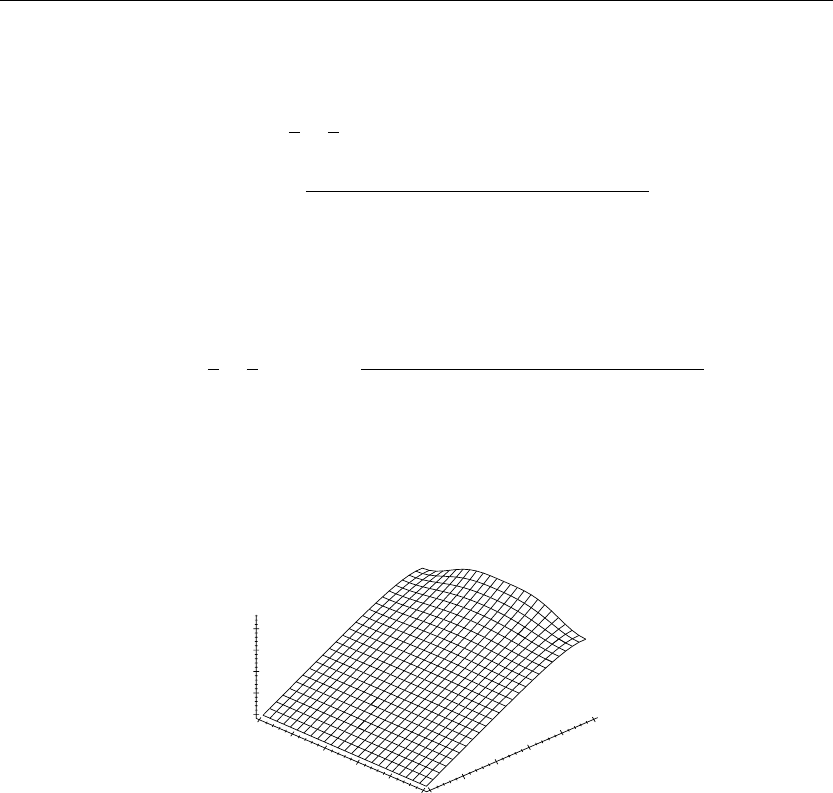
Figure 5.2

The three-dimensional surface shown in Figure 5.2 depicts the steady-state temperature

distribution u(x, y) over the rectangular region. Note how the edges of the surface adhere to

the given boundary conditions. The temperature isotherms can be obtained from Maple by

clicking on the ﬁgure, choosing the special option “Render the plot using the polygon patch

and contour style” in the graphics bar, and then clicking the “redraw” button.

EXAMPLE 5.4.3: We seek the steady-state temperature distribution in a thin rectangular plate

over the domain D ={(x, y) |0 <x<1, 0 <y<1} whose lateral surface is insulated. The side

y = 1 is insulated, the sides x = 1 and y = 0 are held at a ﬁxed temperature of zero, and the

side x = 0 follows the temperature distribution u(0,y)= f(y) given as follows.

292 Chapter 5

SOLUTION: The homogeneous Laplace equation is

∂

∂x

u(x, y) +

∂

∂y

u(x, y) = 0

The boundary conditions are

u(0,y)= y(1 −y) and u(1,y)= 0

and

u(x, 0) = 0 and u

(x, 1) = 0

Here, we see that the boundary conditions are homogeneous with respect to the y variable.

Ordinary differential equations from the method of separation of variables are

X(x)−λX(x)= 0

and

Y(y) +λY(y) = 0

Homogeneous boundary conditions on the y equation are type 1 at y = 0 and type 2 at y = 1

Y(0) = 0 and Y

(1) = 0

Assignment of system parameters

> restart:with(plots):a:=1:b:=1:

Allowed eigenvalues and corresponding orthonormal eigenfunctions for the y equation are

obtained from Example 2.5.2.

> lambda[n]:=((2*n−1)*Pi/(2*b))ˆ2;

(2n −1)

(5.39)

for n = 1, 2, 3,....

Orthonormal eigenfunctions

> Y[n](y):=sqrt(2/b)*sin((2*n−1)*Pi/(2*b)*y);Y[m](y):=subs(n=m,Y[n](y)):

(y) :=

√

2 sin



(2n −1)πy



(5.40)

Statement of orthonormality with respect to the weight function w(y) = 1

The Laplace Par tial Differential Equation 293

> w(y):=1:Int(Y[n](y)*Y[m](y)*w(y),y=0..b)=delta(n,m);



2 sin



(2n −1)πy



sin



(2m −1)πy



dy = δ(n, m) (5.41)

Basis vectors for the x equation

> x1(x):=sinh(sqrt(lambda)*(a−x));x2(x):=cosh(sqrt(lambda)*(a−x));

x1(x) := sinh



√

λ(1 −x)



x2(x) := cosh



√

λ(1 −x)



(5.42)

General solution to the x equation

> X[n](x):=A(n)*cosh((2*n−1)*Pi/(2*b)*(a−x))+B(n)*sinh((2*n−1)*Pi/(2*b)*(a−x));

(x) := A(n) cosh



(2n −1)π(1 −x)



+B(n) sinh



(2n −1)π(1 −x)



(5.43)

Substituting into the x-dependent boundary condition yields

> eval(subs(x=a,X[n](x)))=0;

A(n) = 0 (5.44)

The x-dependent solution

> X[n](x):=B(n)*sinh((2*n−1)*Pi/(2*b)*(a−x));

(x) := B(n) sinh



(2n −1)π(1 −x)



(5.45)

Generalized series terms

> u[n](x,y):=X[n](x)*Y[n](y);

(x, y) := B(n) sinh



(2n −1)π(1 −x)



√

2 sin



(2n −1)πy



(5.46)

Eigenfunction expansion

> u(x,y):=Sum(u[n](x,y),n=1..inﬁnity);

u(x, y) :=

∞



n=1

B(n) sinh



(2n −1)π(1 −x)



√

2 sin



(2n −1)πy



(5.47)

Evaluation of Fourier coefﬁcients from the speciﬁc remaining boundary condition

u(0,y)= f(y)

294 Chapter 5

> f(y):=y*(1−y);

f(y) := y(1 −y) (5.48)

Substituting this condition into the preceding solution yields

> f(y)=subs(x=0,u(x,y));

y(1 −y) =

∞



n=1

B(n) sinh



(2n −1)π



√

2 sin



(2n −1)πy



(5.49)

The preceding equation is the Fourier series expansion of f(y) in terms of the orthonormalized

Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier cofﬁcients, we take the

inner product of both sides with respect to the orthonormalized eigenfunctions, and, taking

advantage of the previous statement of orthonormality, we get, for n = 1, 2, 3,...,

> B(n):=(1/sinh((2*n−1)*Pi*a/(2*b)))*Int(f(y)*Y[n](y)*w(y),y=0..b);B(n):=value(%):

B(n) :=



y(1 −y)

√

2 sin



(2n −1)πy



sinh



(2n −1)π



(5.50)

> B(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn,sin((2*n+1)*Pi/2)=(−1)ˆn,

cos((2*n+1)*Pi/2)=0},B(n)));

B(n) :=

√

2(4 +2πn(−1)

−π(−1)

)

sinh



(2n −1)π



(8n

−12n

+6n −1)

(5.51)

Generalized series terms

> u[n](x,y):=eval(X[n](x)*Y[n](y));

(x, y) :=

8(4 +2πn(−1)

−π(−1)

) sinh



(2n −1)π(1 −x)



sin



(2n −1)πy



sinh



(2n −1)π



(8n

−12n

+6n −1)

(5.52)

Series solution

> u(x,y):=Sum(u[n](x,y),n=1..inﬁnity);

u(x, y) :=

∞



n=1

8(4 +2πn(−1)

−π(−1)

) sinh



(2n −1)π(1 −x)



sin



(2n −1)πy



sinh



(2n −1)π



(8n

−12n

+6n −1)

(5.53)

First few terms of expansion

> u(x,y):=sum(u[n](x,y),n=1..5):

> plot3d(u(x,y),x=0..a,y=0..b,axes=framed,thickness=1);

The Laplace Par tial Differential Equation 295

0.2

0.15

0.1

0.2

0.4

0.6

0.8

0.6

0.4

0.2

0.8

0.05

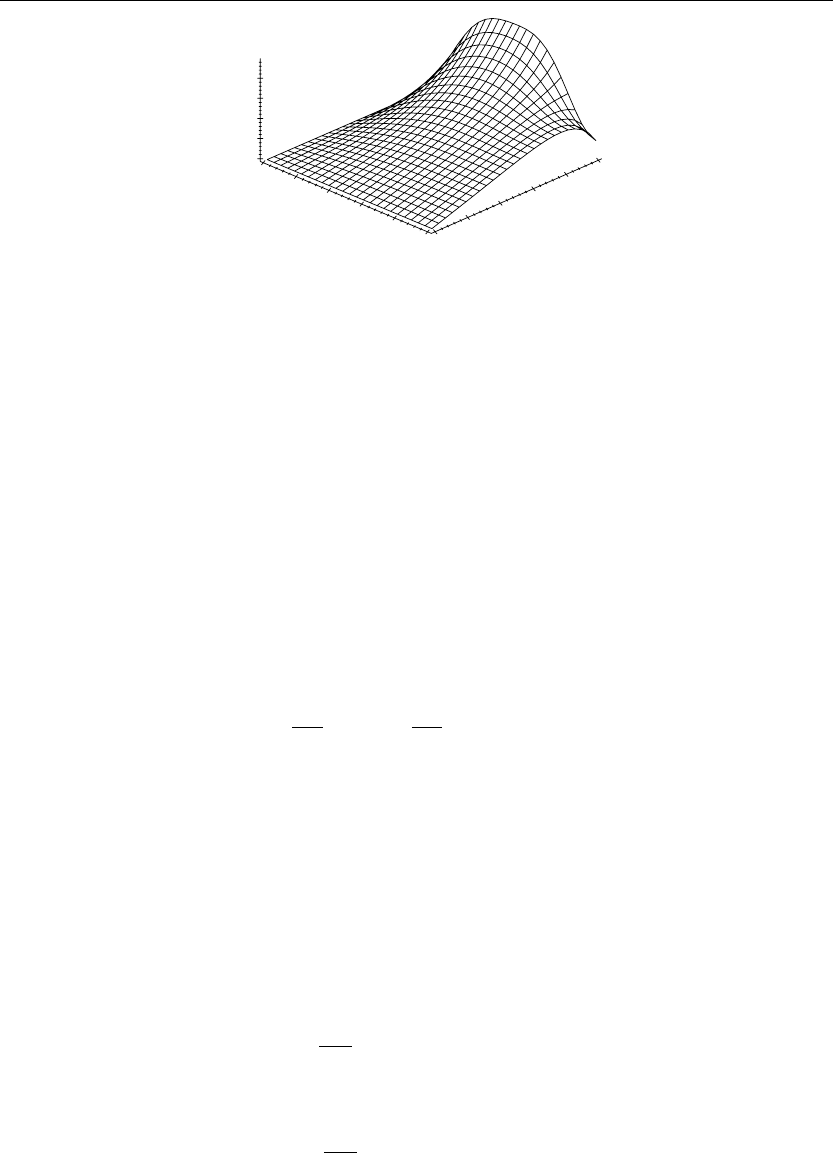
Figure 5.3

The three-dimensional surface shown in Figure 5.3 depicts the steady-state temperature

distribution u(x, y) over the rectangular region. Note how the edges of the surface adhere to

the given boundary conditions. The temperature isotherms can be obtained from Maple by

clicking on the ﬁgure, choosing the special option “Render the plot using the polygon patch

and contour style” in the graphics bar, and then clicking the “redraw” button.

EXAMPLE 5.4.4: We seek the steady-state temperature distribution in a thin rectangular plate

over the domain D ={(x, y) |0 <x<1, 0 <y<1} whose lateral surface is insulated. The side

x = 0 is insulated, the side y = 1 has a ﬁxed temperature of zero, the side y = 0 follows the

temperature distribution f(x), and the side x = 1 is experiencing a convection heat loss into a

zero temperature surrounding.

SOLUTION: The homogeneous Laplace equation is

∂

∂x

u(x, y) +

∂

∂y

u(x, y) = 0

The boundary conditions are

(0,y)= 0 and u(1,y)+u

(1,y)= 0

and

u(x, 0) = 1 −x

and u(x, 1) = 0

Here, we see that the boundary conditions are homogeneous with respect to the x variable.

Ordinary differential equations from the method of separation of variables are

X(x)+λX(x) = 0

and

Y(y) −λY(y) = 0

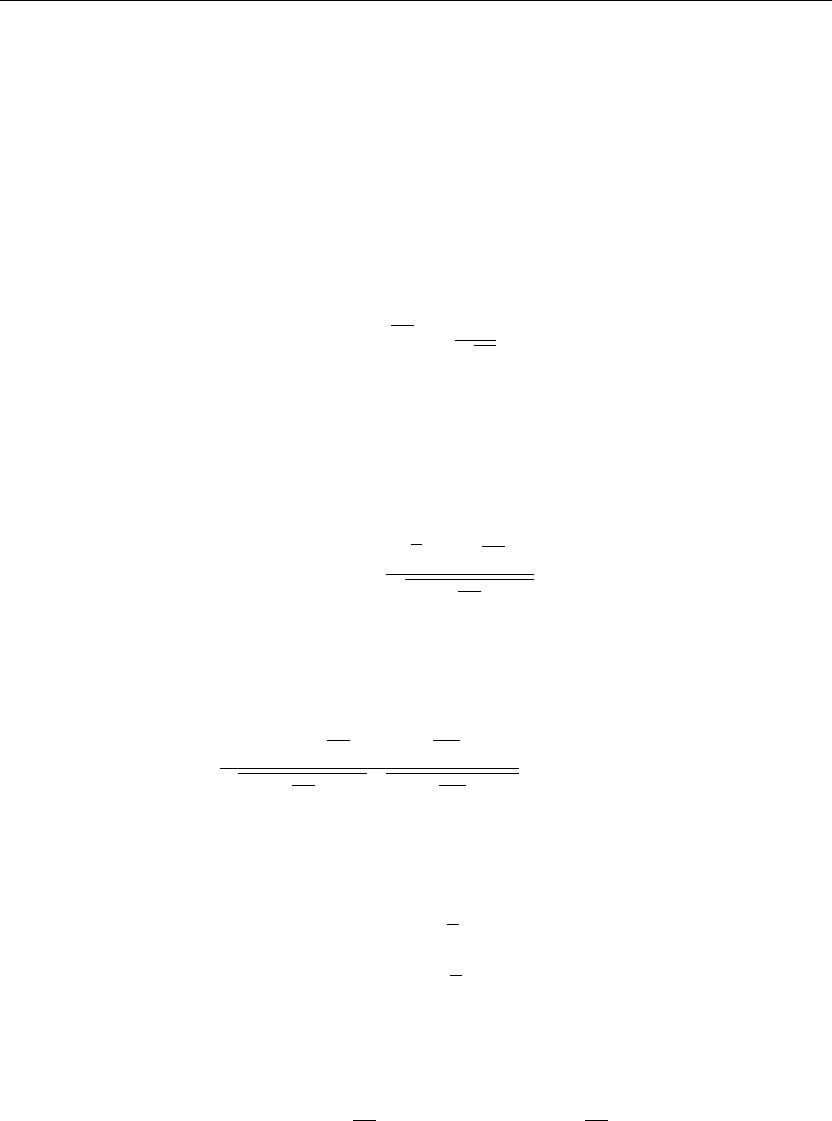
296 Chapter 5

Homogeneous boundary conditions on the x equation are type 2 at x = 0 and type 3 at x = 1:

(0) = 0 and X

(1) +X(1) = 0

Assignment of system parameters

> restart:with(plots):a:=1:b:=1:

Allowed eigenvalues and corresponding orthonormal eigenfunctions for the x equation are

obtained from Example 2.5.5. The eigenvalues are the roots of the eigenvalue equation

> tan(sqrt(lambda[n])*a)=1/sqrt(lambda[n]);

tan







√

(5.54)

for n = 1, 2, 3,....

Orthonormal eigenfunctions

> X[n](x):=sqrt(2)*cos(sqrt(lambda[n])*x)/sqrt(((sin(sqrt(lambda[n])*a))ˆ2+a));X[m](x):=

subs(n=m,X[n](x)):

(x) :=

√

2 cos



√





sin



√



(5.55)

Statement of orthonormality with respect to the weight function w(x) = 1

> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=0..a)=delta(n,m);



2 cos



√



cos



√





sin



√





sin



√



dx = δ(n, m) (5.56)

Basis vectors for the y equation

> y1(y):=sinh(sqrt(lambda)*(b−y));y2(y):=cosh(sqrt(lambda)*(b−y));

y1(y) := sinh



√

λ(1 −y)



y2(y) := cosh



√

λ(1 −y)



(5.57)

General solution to the y equation

> Y[n](y):=A(n)*cosh(sqrt(lambda[n])*(b−y))+B(n)*sinh(sqrt(lambda[n])*(b−y));

(y) := A(n) cosh





(1 −y)



+B(n) sinh





(1 −y)



(5.58)

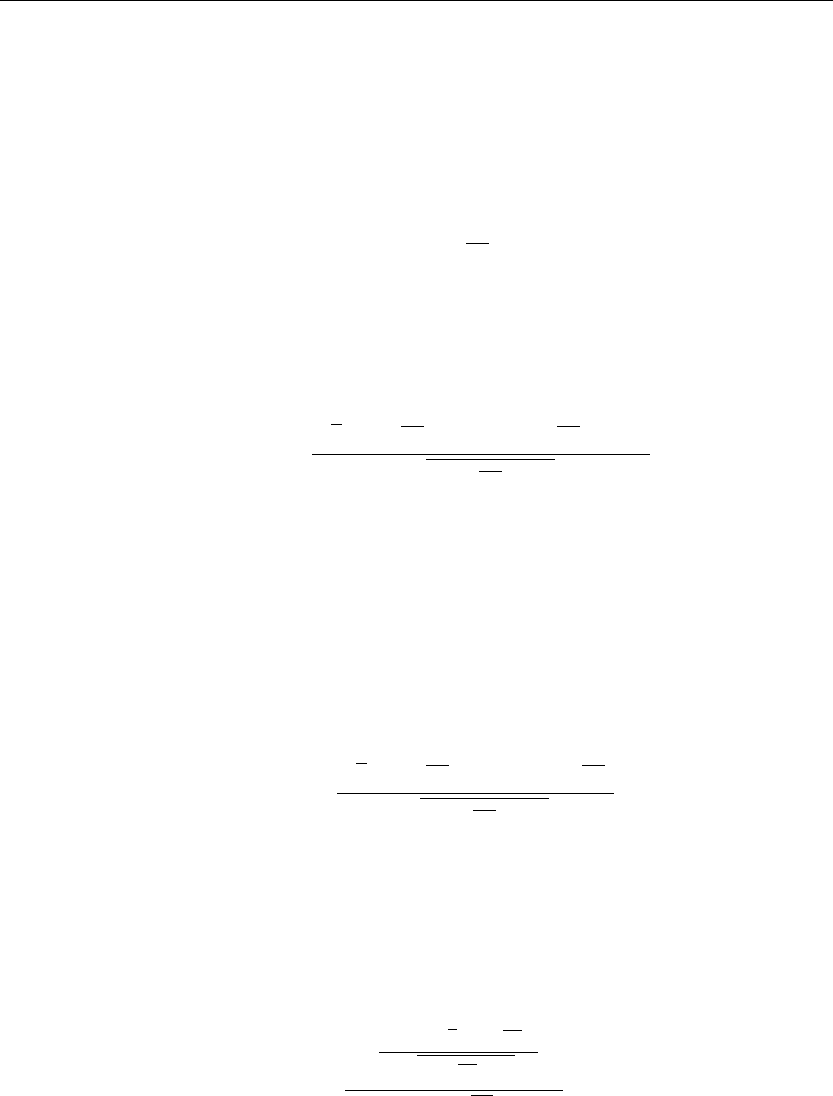
The Laplace Par tial Differential Equation 297

Substituting into the y-dependent boundary condition yields

> eval(subs(y=b,Y[n](y)))=0;

A(n) = 0 (5.59)

The y-dependent solution

> Y[n](y):=B(n)*sinh(sqrt(lambda[n])*(b−y));

(y) := B(n) sinh





(1 −y)



(5.60)

> u[n](x,y):=X(n)(x)*Y[n](y):

Eigenfunction expansion

> u(x,y):=Sum(u[n](x,y),n=1..inﬁnity);

u(x, y) :=

∞



n=1

√

2 cos



√



B(n) sinh



√

(1 −y)





sin



√



(5.61)

Evaluation of Fourier coefﬁcients from the speciﬁc remaining boundary condition

u(x, 0) = f(x)

> f(x):=1−xˆ2;

f(x) := 1 −x

(5.62)

Substituting this condition into the preceding solution yields

> f(x)=subs(y=0,u(x,y));

1 −x

∞



n=1

√

2 cos



√



B(n) sinh



√





sin



√



(5.63)

This equation is the Fourier series expansion of f(x) in terms of the orthonormal

Sturm-Liouville eigenfunctions found earlier. To evaluate the Fourier coefﬁcients, we take the

inner product of both sides with respect to the orthonormal eigenfunctions, and, taking

advantage of the previous statement of orthonormality, we get, for n = 1, 2, 3,...,

> B(n):=(1/sinh(sqrt(lambda[n])*b))*Int(f(x)*X[n](x)*w(x),x=0..a);B(n):=value(%):

B(n) :=



(1−x

)

√

2 cos



√





sin



√



sinh



√



(5.64)

Substitution of the eigenvalue equation simpliﬁes the preceding equation