Архіпова О.С. Вища математика
Подождите немного. Документ загружается.

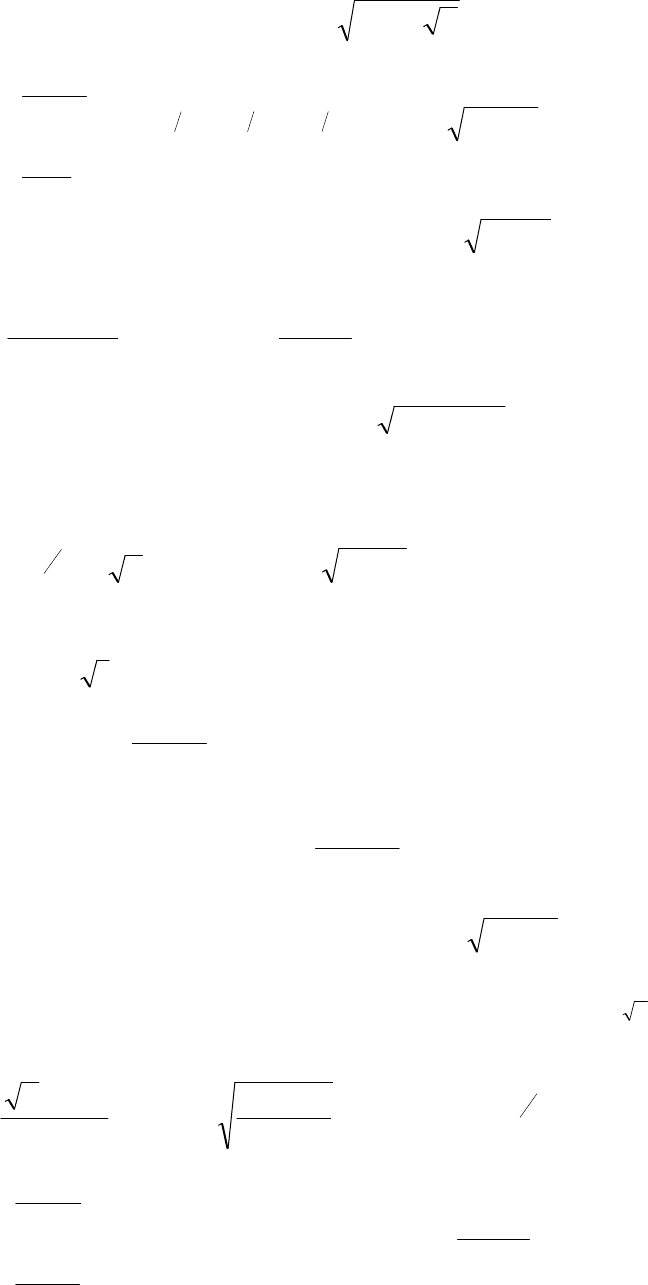
111
5.1.15.
( )
1 3 3 2 3 2
4
1
1
5 6 9 4 01
3 2
3
2
2
3
2 3 2 3 2 3 2
) ln arccos ; ) ln ; ) sin ;
)
,
;
) ; ) , , .
y e x x y tg x y x
x
t
t
y
t
t
x y a y x x
x
ctg x
= − = =
=
−
=
+
+ = = + =
7)
Написати рівняння нормалі до кривої
y x
= +
1
2
у
точці
з
абсцисою
x
0
=0.
5.1.16.
( )
1
7 3
4
2
2
3 5
4
3
3
5 6 3 0 01
2
5
5
3
)
cos
ln
; ) sin ; ) sin ;
)
cos ,
sin ;
) ; ) cos , , .
cos
y
x
x
y
x x
x
y x
x t
y t
tgy atgx y x x x
x
t
t
=
+
+
=
−
−
=
=
=
= = + =
7)
До
кривої
y=xsin2x
написати
рівняння
дотичної
,
паралельної
прямій
y+
π
x+9=0.
5.1.17
(
)
( )
1 4 1 2 1 3 5
4
1
5 6 0 97
3
2
4
3
3
3
5
3
2 2
) ; ) sin ; ) ;
)
ln ,
;
) ( ); ) , , .
y x x x y x y x
x t t
y t t
y tg y x y arctgx x
ctg x
= + − = + = +
=
= −
= − = =
−
7)
До
кривої
y
x
x
=
+
+
3
2
1
4
написати
рівняння
дотичної
і
нормалі
у
точці
з
абсцисою
x
0
=-1.
5.1.18.
( )
( )
1 2 2 5 3 2
3
3 3
4
1
5 6 2 4 97
3
5
3
2
2
3
) cos ; )
ln
cos
; ) cos ;
)
cos ,
sin ;
) arcsin ; ) , , .
sin
y x tg x y
x
x
y x
x t t
y t t
e x y x x
x
x
xy
= ⋅ − = =
=
= −
= = + =
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y e
x
=
−1
у
точці
з
ординатою
y
0
=e.
5.1.19
( )
1
3
1 4
2
2
2
3 5
4
3
2
1
5 6
2
1
107
3
3
2
3 2 3
3
2
3
)
cos
; )
sin
sin
; ) ;
)
,
ln
;
) ; ) , , .
y
x tg x
x
y
x
x
y ctg x
x
t
t
y
t
t
x ax y y a y
x
x
x
x
=
⋅
+
=
−
+
=
=
−
=
+
+ + = =
−
+
=
7)
До
кривої
y=cosx
написати
рівняння
дотичної
,
паралельної
до
прямої
y+x+3=0.
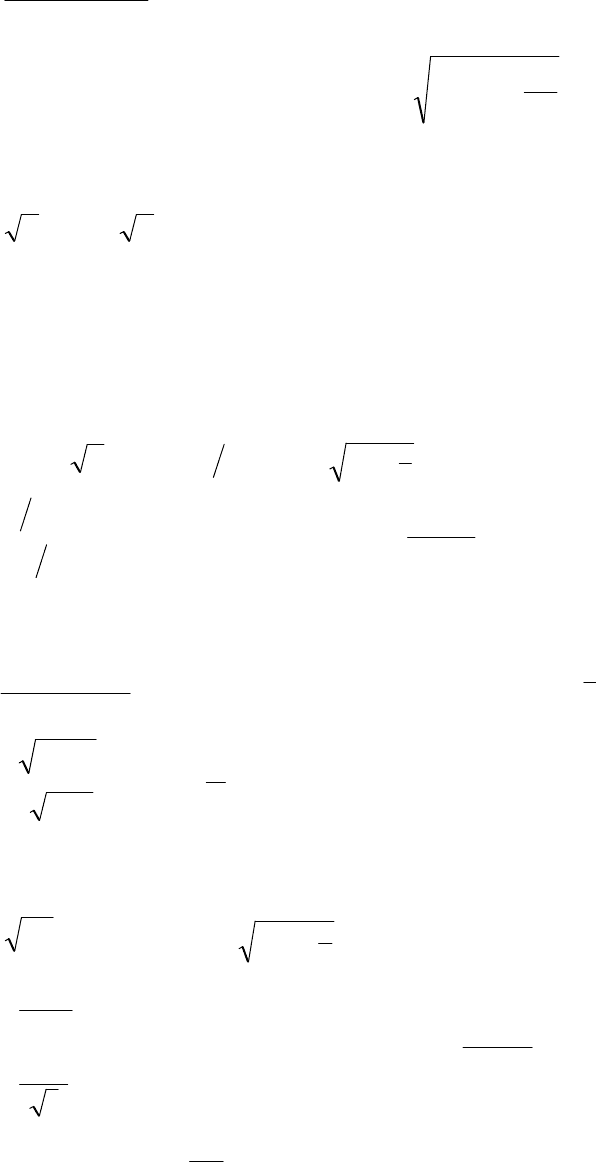
112
5.1.20.
(
)
( )
1
2
3 3
2 3 3
4 5 6 2
2
103
3
3
3
4
)
arcsin
; ) arcsin cos ; ) arcsin ;
)
cos ,
sin ;
)cos( ) ; ) sin , , .
y
x x
x arctg x
y x y x
x t
y t
xy e y x
x
x
x
x y
=
+
+
= =
=
=
= = − =
+
π
7)
До
лінії
y=x
3
-3x
2
-5
скласти
рівняння
дотичної
,
перпендикулярної
прямій
2x-6y+1=0.
5.1.21.
(
)
(
)
(
)
( )
( )
1 3 6 2 3 3
4
1
5 2 6 1 2 2 03
3
2 2
3
2
3
) ; ) arccos sin ; ) ;
)
sin ,
cos ;
) ln ; ) , , .
y x x x y x y arctg x
x t t
y t
y y e y x x x
x
x
= − + = =
= −
= −
= = − + =
+
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y=xln(1+x2)
у
точці
з
абсцисою
x
0
=1.
5.1.22.
(
)
.93,0,
1
1
)6);ln(2)5
;)1(
,)1(
)4
;5)3;ln)2;)5)1(()1
2
22
2
7
4
3
32
−=
−
+
=+=
−=
−=
==−+=
+
+
x
x
x
yyx
tty
ttx
xarctgytgyxxtgxxy
yx
x
x
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y=sinx+cosx
у
точці
з
абсцисою
x
0
=π/4.
5.1.23.
( ) ( )
.,x,xarcsiny);yln
y
x
arctg)
;tty
,tx
)
;xsiny);xctglnxlny);
xcos
xarctge
y)
x
x
2490265
1
1
4
3332
4
3
1
3
5
3
2
===
+=
+=
=+==
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y
x x
=
−
4
2
у
точці
з
абсцисою
х
0
=1.
5.1.24.
( )
1 3 2 3 5
4
2
1
5 3 2 0 6
1
1
102
3
4
2
2
3
7
3
2
2
) ; ) lnsin ; ) arccos ;
)
,
;
) ln ; ) , , .
y x y y x
x
t
t
y
t
t
y y a x y
x
x
x
x
x
x
= + = =
=
−
=
−
− + = =
−
+
=
−
+
7)
До
кривої
2
x
1
1y −=
написати
рівняння
дотичної
,
паралельної
до
прямої
2y+32x+7=0.
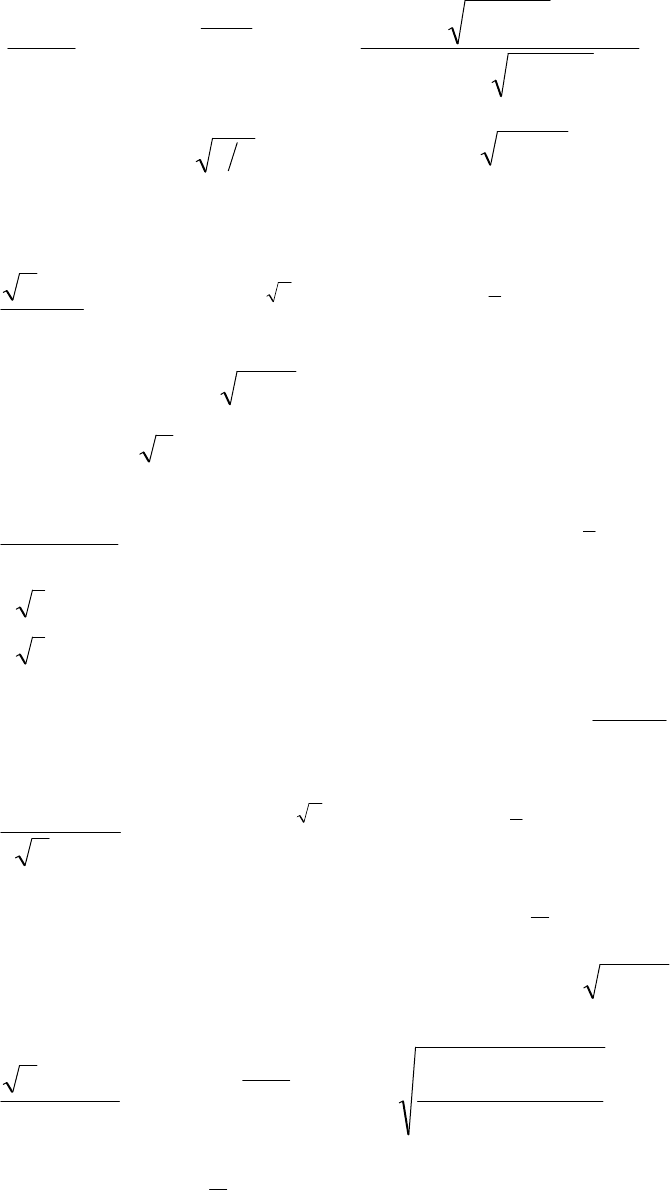
113
5.1.25.
( ) ( ) ( )
( )
( )
1
2
2 4 3
1 1 3
1 1
4
1
5 6 5 0 98
2
2
2 5
3
3
2
5
3
5
2
)
sin
; ) ; ) ;
)
,
cos ;
) sin ln ; ) , , .
cos
y
xe
x
y y
x x x
x x
x t
y t
arctg x y y a y x x
x
x
x
= = =
− + −
+ −
=
= −
+ = = − =
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y=x-arctgx
у
точці
з
абсцисою
х
0
=1.
5.1.26.
( )
( )
1
2
3
2 5 3 5
4 5 6 2 014
3
7
2
3
2
)
sin
; ) ; ) ;
)
sin ln ,
cos ln ;
)sin ln ; ) , , .
ln
y
x
x
y y ctg x
x t t
y t t
x y tgy y e x
x
ctg x
x
x x
=
⋅
= =
= +
= +
+ = = =
−
7)
До
кривої
y x x= −
написати
рівняння
нормалі
,
перпендикулярної
до
прямої
4y-3x+5=0.
5.1.27.
( ) ( )
( ) ( )
1
4
2 3 2
4 5 2 6 3 1 1 101
2
3
3
2
)
ln
; ) ln ln ln ; ) cos ;
)
,
;
)arcsin ; ) , , .
y
x arctg x
x
y x x y x
x t
y t
xy y x x x
x
x
=
⋅
= + =
=
=
= = − + =
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y
x
x
=
−
−
3
2
2
4
у
точці
з
абсцисою
х
0
=3.
5.1.28.
( )
( )
1
3
2 3 3 4
4 5 6
2
2 031
2
4
2
6
2
)
sin
; ) ; ) ;
)
cos sin ,
sin cos ;
) ln( ) ; ) , , .
ln
y
e x
x x
y y tg x
x t t t
y t t t
x x y a y arctg
x
x
x
tg x
x
=
⋅
+
= =
= +
= −
+ = = =
7)
Написати
рівняння
дотичної
і
нормалі
до
кривої
y x= −
2
3
1
у
точці
з
абсцисою
х
0
=1.
5.1.29.
(
)
1
5
2 5 3
1 2
2
4
1
5 2 6 2 5 2 03
2
3
2 3
2
3
3
4 2
)
cos
; ) ; )
sin
;
)
sin ,
;
)arccos ; ) , , .
sin
y
x x
e
y y
x x x
x
x t
y t
x
y
y x x x
x
x
x
a
=
⋅
= =
+
−
=
= +
= = − + =
7)
Написати рівняння дотичної і нормалі до кривої y xe
x
=
−
2
у точці з
абсцисою х
0
=1.
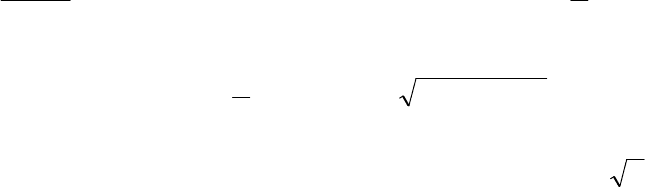
114
5.1.30.
( )
( )
( )
1
1
1
2 2 2 3
5
4
1
1
5 6 1 0 02
2
2
3
3
3
2
) arcsin ; ) cos sin ; ) cos ;
)
;
;
)ln ; ) sin ; , .
y
x
x
x y x y
x
x e t
y e t
tg
y
x
a y x x x
x
t
t
=
−
+
= =
= +
= −
= = + + =
7)
Написати рівняння дотичної і нормалі до кривої y x x= +
3
3
у точці з
абсцисою х
0
=-1.

115
РОЗДІЛ 6
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ, МЕТОДИ ІНТЕГРУВАННЯ
6.1. Первісна, властивості невизначеного інтеграла
Функція F(x) є первісна для функції f(x) на інтервалі (a, b), якщо F(x)
диференційовна
(
)
b,ax
∈
∀
й
(
)
(
)
xfxF
=
′
.
1
о.
Якщо F(x) є первісною на інтервалі (a,b), то F(x)+С, де С – довільна
постійна, також є первісною.
2
о.
Якщо
(
)
xF
1
й
(
)
xF
2
– будь-які дві первісні, то
(
)
(
)
CxFxF
=
−
21
,
звідки
(
)
(
)
CxFxF
+
=
21
.
Сукупність первісних F(x)+С називається невизначеним інтегралом і
позначається
(
)
(
)
∫
+= CxFdxxf .
Властивості невизначеного інтеграла
( )
(
)
( )
( )
( )
( )
( ) ( )
( ) ( )
( )
∫ ∫∫
∫∫
∫
∫
∫
±=±
=
+=
=
=
′
.vdxudxdxvu.
.dxxfCdxxCf.
.CxFxdF.
.dxxfdxxfd.
.xfdxxf.
o
o
o
o
o
5
4
3
2
1
Таблиця основних невизначених інтегралів
( )
.nC
n
x
dxx.
.Cxdx.
n
n
1
1
2
1
1
−≠+
+
=
+=
+
∫
∫
13.
2 2
2 2
ln
dx
x x a C
x a
= + ± +
±
∫
.
14.
tg ln cos .
xdx x C
= − +
∫
( )
( )
.aC
a
ln
a
dxa.
.xCxln
x
dx
.
x
x
104
03
≠<+=
≠+=
∫
∫
15.
ctg ln sin .
xdx x C
= +
∫
16.
2 2
1 1
arctg .
dx x x
c arcctg c
x a a a a a
= + = − +
+
∫
5.
.
x x
e dx e C
= +
∫
6.
cos sin .
xdx x C
= +
∫
17.
2 2
arcsin arccos
dx x x
c c
a a
a x
= + = − +
−
∫
.
7.
sin cos
xdx x C
= − +
∫
. 18.
ln tg
sin 2
dx x
C
x
= +
∫
.
8.
2
tg
cos
dx
x C
x
= +
∫
. 19.
ln tg .
cos 2 4
dx x
C
x
π
= + +
∫
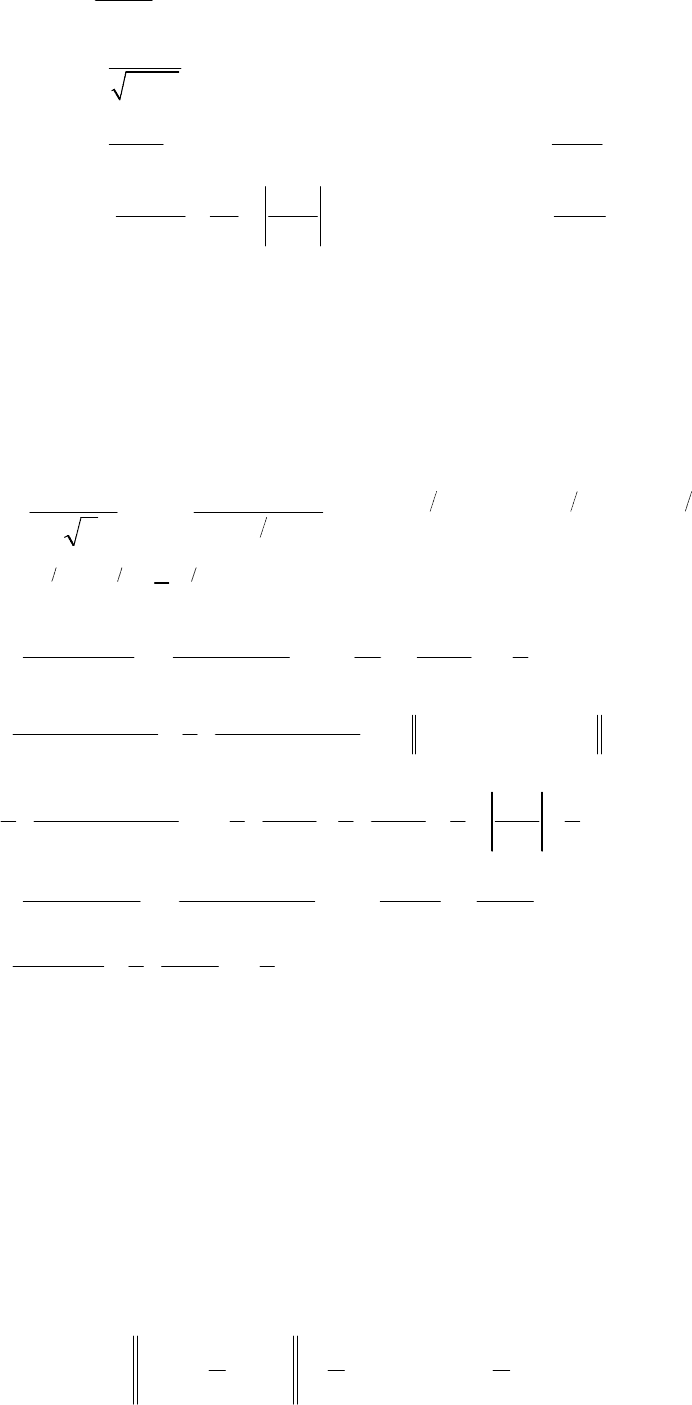
116
9.
2
ctg
sin
dx
x C
x
= − +
∫
. 20.
.
shx dx chx C
= +
∫
10.
2
arcsin
arccos
1
x C
dx
x C
x
+
=
− +
−
∫
. 21.
ch sh
xdx x C
= +
∫
.
11.
2
arctg .
arcctg .
1
x C
dx
x C
x
+
=
− +
+
∫
22.
2
cth .
sh
dx
x C
x
= − +
∫
12.
2 2
1 -
ln .
2
dx x a
c
x a a x a
= +
− +
∫
23.
2
th
ch
dx
x C
x
= +
∫
.
При інтегруванні функцій можливість безпосередньо використати основні
формули буває вкрай рідкою. Як правило, підінтегральну функцію
доводиться так чи інакше перетворювати для того, щоб інтеграл звести до
табличного. Нижче наведені приклади таких перетворень.
Приклади.
(
)
=++=
++
=
+
∫∫∫∫∫
−−
dxxdxxdxxdx
x
xx
dx
xx
x
.
212123
23
2
2
2
211
1
( )
( )
( )
( )
( )( ) ( )( )
( )
( )
( )( )
1 2 1 2 3 2
2 2 2
2 2
2 2 2 2
2 2
2 2 2 2
2 2
2 2
2 2
2
2
2 4 .
3
1 2 1
1
2. .
1
1 1
1 2
3. 1 1 2
2
1 1 1 1
1 1
1 1 1 1 1 1
ln .
2 2 1 2 1 4 1 2
1 1
4.
sin co
x x x C
x dx x x
dx dx
dx arctgx C
x x x
x x x x
dx
dx x x
x x x x
x x
dx dx x
dx arctgx C
x x x
x x
dx
x
−
= − + + +
+ + +
= = + = − + +
+
+ +
= = + − − ≡ =
− + − +
+ − −
−
= = − = − +
− + +
− +
∫ ∫ ∫ ∫
∫ ∫
∫ ∫ ∫
2 2
2 2 2 2 2
2
sin cos
.
s sin cos cos sin
1 1
5.
1 cos2 2 sin 2
x x dx dx
dx tgx ctgx C
x x x x x
dx dx
ctgx C
x x
+
= = + = − +
= = − +
−
∫ ∫ ∫ ∫
∫ ∫
Зауваження. При інтегруванні однієї й тієї ж функції результати
можуть бути по своєму зовнішньому вигляду різними. У дійсності ж вони
або тотожні, або відрізняються між собою тільки на постійну величину.
Теорема (про інваріантость формул інтегрування). Вид формули
інтегрування залишається незмінним незалежно від того, чи є змінна
інтегрування незалежною змінною чи деякою диференційовною функцією;
тобто, якщо
(
)
(
)
CxFdxxf +=
∫
, то
(
)
(
)
(
)
(
)
CxF)x(dxf +=
∫
ϕϕϕ
.
Наведена теорема дозволяє багато інтегралів приводити до табличних.
Приклади.
1.
(
)
(
)
Cexdexdxdxdxxe
xxx
+====
∫∫
222
2
1
2
1
2
1
22
.
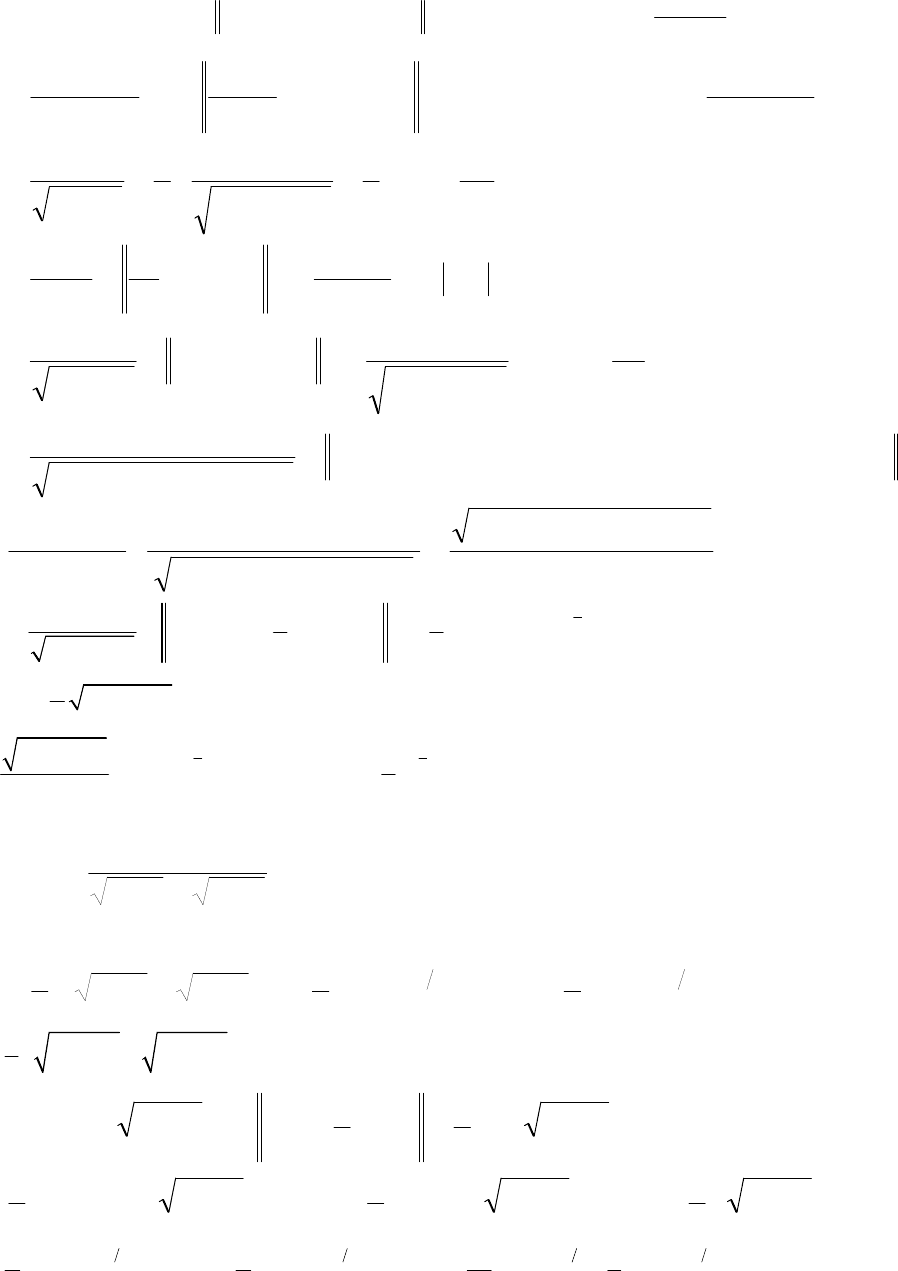
117
2.
( ) ( )
.C
xsin
xsinxdsinxsindxdxcosxdxcosxsin +====
∫∫
6
6
55
3.
(
)
( ) ( ) ( )
(
)
.C
arctgx
arctgxdarctgxarctgxd
x
dx
dx
x
arctgx
+===
+
=
+
∫∫
3
11
3
2
22
2
4.
(
)
( )
.C
x
arcsin
x
xd
x
xdx
+=
−
=
−
∫∫
22
1
2
2
1
4
2
2
22
2
4
5.
( )
(
)
.Cxlnln
xln
xlnd
xlnd
x
dx
xlnx
dx
+====
∫∫
6.
(
)
(
)
( )
.C
e
arcsin
e
ed
eddxe
e
dxe
x
x
x
xx
x
x
+=
−
===
−
∫∫
2
2
4
2
2
2
7.
(
)
(
)
=+=−=
+
∫
xcosbxsinadxdxcosxsinba
xcosbxsina
xdxcosxsin
222222
2222
2
( )
(
)
( )
C
ba
xcosbxsina
xcosbxsina
xcosbxsinad
ba
+
−
+
=
+
+
−
=
∫
22
2222
2222
2222
22
2
1
,
b
a
≠
.
8.
( )
1
2
cos5 1 1
cos5 sin5 (3 sin5 ) (3 sin5 )
5 5
3 sin5
2
3 sin5 .
5
xdx
xdx d x x d x
x
x c
−
= = = − − −
−
= − − +
∫ ∫
2 2 5
3
3 3
ln (1 )
3
ln (1 ) ln(1 ) ln (1 )
1 5
x
dx x d x x C
x
+
= + + = + +
+
∫ ∫
9.
.
10.
∫
−++
=
1x1x
dx
J
.
Якщо позбавитися від ірраціональності в знаменнику, одержимо:
(
)
( ) ( ) ( ) ( )
=−−−++=−−+=
∫∫ ∫
1xd1x
2
1
1xd1x
2
1
dx1x1x
2
1
J
2121
( ) ( )
3 3
1
1 1
3
x x C
= + − − +
.
11.
(
)
(
)
=+===+=
∫∫
2
3
222
3
23
1
2
1
2
1
1
xdxxxdxdxdxxxI
(
)
(
)
(
)
(
)
(
)
=++−+++=++−+=
∫∫∫
11
2
1
111
2
1
1111
2
1
2
3
22
3
222
3
22
xdxxdxxxdxx
( ) ( ) ( ) ( ) ( ) ( )
4 3 1 3 7 3 4 3
2 2 2 2 2 2
1 1 3 3
1 1 1 1 1 1
2 2 14 8
x d x x d x x x C
= + + − + + = + − + +
∫ ∫
.

118
12.
2
В чисельнику запишемо похідну знаменник
а
і виконаємо перетворення таким чином,
3 1
щоб одержаний вираз в чисельнику
4 4 17
був рівним початковому
x
I dx
x x
−
=
− +
∫
=
2
2 2
2
3 3
(8 4) 1
3 (4 4 17) 1
8 2
17
4 4 17 8 4 4 17 8
4
x
d x x dx
dx
x x x x
x x
− + −
− +
= +
− + − +
− +
∫ ∫ ∫
.
Виділимо повний квадрат:
2
2
17 1
4
4 2
x x x
− + = − +
;
( )
2 2
2
2
1
3 1 3 1 2 1
2
ln 4 4 17 ln(4 4 17)
8 8 8 16 4
1
2
2
d x
x
I x x x x arctg c
x
−
−
= − + + = − + + +
− +
∫
.
13.
1
2 2
2
2 2 2
2 5 (2 6) 1 ( 3)
( 6 2) ( 6 2)
6 2 6 2 ( 3) 7
x x d x
I dx dx x x d x x
x x x x x
−
+ + − +
= = = + + + + −
+ + + + + −
∫ ∫ ∫ ∫
=
2 2
2 6 2 ln 3 6 2
x x x x x c
+ + − + + + + +
.
6.2. Методи інтегрування
6.2.1. Метод заміни змінної
Одним з основних методів обчислення інтегралів є метод заміни
змінної, суть якого полягає в тому, що якщо
(
)
x t
ϕ
=
– неперервно
диференційовна монотонна функція, то
(
)
(
)
(
)
(
)
∫∫
′
= dtttfdxxf
ϕϕ
.
Нижче цей метод проілюстрований на ряді прикладів.
Приклади.
1.
2
2 2
2
1 ,
( 1) 1
1 ,
( 1)
1 1 1
1 1
2 2 ,
x t
xdx tdt t dt
x t
dt dt dt d t
t t t
x
xdx tdt
xdx tdt
+ =
+ −
+ =
= = = − = +
+ + +
+ +
=
=
∫ ∫ ∫ ∫ ∫
2 2
ln(1 ) 1 ln(1 1 )
t t c x x c
− + + = + − + + +
.
2.
4 3 3 2
,
( 1) 1 ( 1)( 1)
1 1 1 1 1
x
x
x
x
e t
e t t t t t dt
dx dt dt dt
e t t t t
e dx dt
=
− + − + +
= = = +
− − − − −
=
∫ ∫ ∫ ∫ ∫
=
3 2 3 2
ln 1 ln 1
3 2 3 2
x x
x x
t t e e
t t c e e c
+ + + − + = + + + − +
.
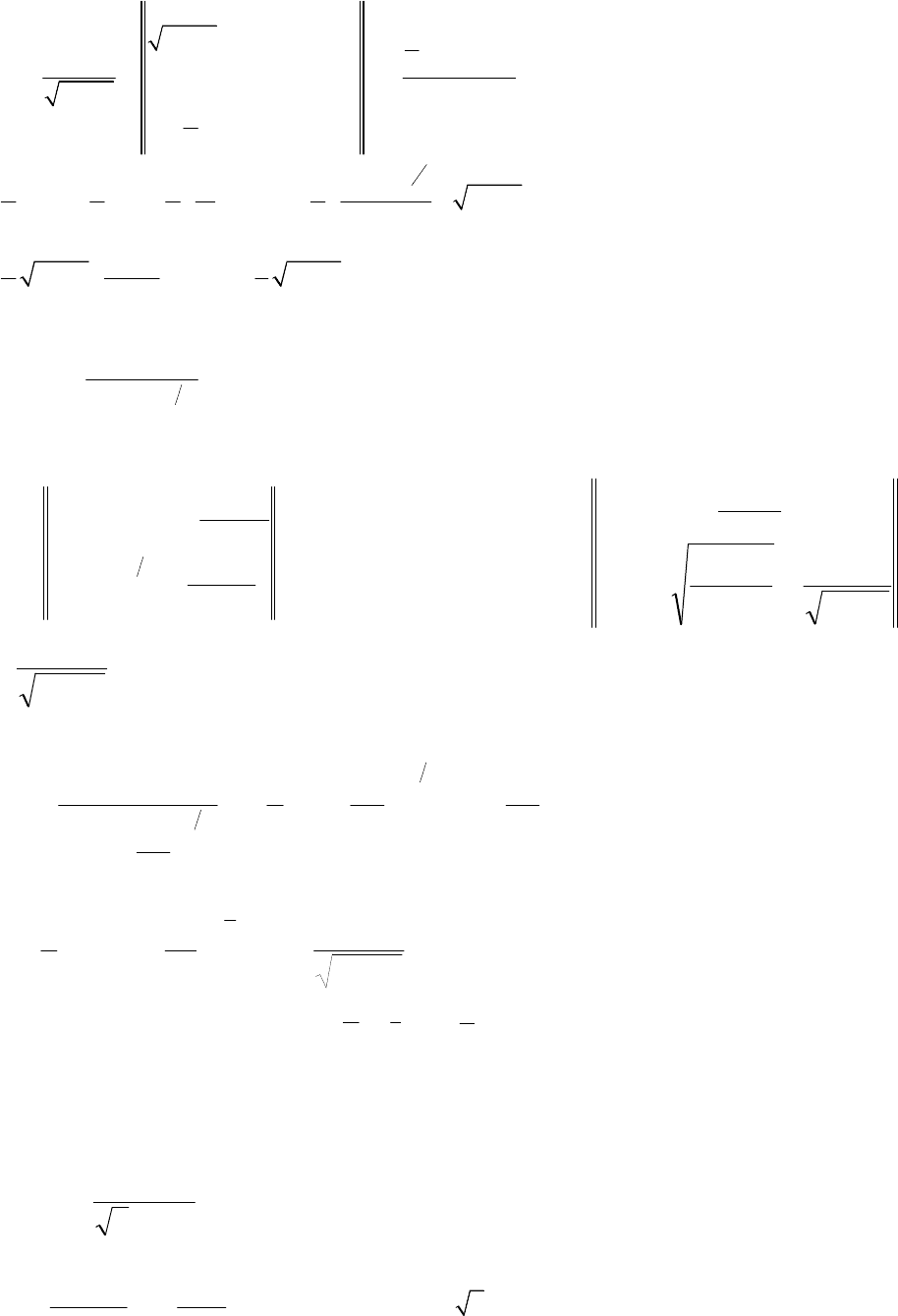
119
3.
( )
( )
2
2
2
1
2 1 , 2 1 ,
1 1
1
2
2 2 , ,
2 1
1
1
2
x t x t
t
x
dx dx tdt dx tdt tdt
t
x
x t
− = − =
+ −
−
= = = =
−
= +
∫ ∫
3
3
2
2
1 1 1 1 (2 1)
2 1
2 2 2 3 2 3
t x
t dt dt t c x c
−
− = − + = − − +
∫ ∫
=
1 2 1 1
2 1 1 2 1( 2)
2 3 3
x
x c x x c
−
− − + = − − +
.
4.
(
)
∫
+
=
23
2
1x
dx
I
.
1-й спосіб (заміна змінної).
( )
tcos
x
tcos
dt
dxtgtx
I
3
23
2
2
1
1
=+
==
=
;
∫
=+== CtsintdtcosI =
2
2
2
2
2
1
1
1
1
x
x
ttg
ttg
tsin
tsin
tctg
+
=
+
=
=+
=
C
x1
x
2
+
+
.
2-й спосіб (безпосереднє обчислення).
∫ ∫
=
+
+−=
+
=
−
2
23
223
2
3
1
1
1
1
2
1
1
1
x
d
x
x
x
dx
I
( )
.C
x1
x
C
x
1
12
2
1
2
2
1
2
+
+
=+
+−−=
−
Інтеграли виду: ,dxx,...,x,xR
r
p
s
l
n
m
∫
де R – раціональна функція
своїх аргументів, обчислюються заміною
k
t
x
= (k – загальний знаменник
дробів), що дозволяє позбутися від ірраціональностей.
5.
( )
.
xx
dx
I
∫
+
=
1
У даному прикладі k=2, тому слід зробити заміну
2
x t
=
. Тоді
( )
2
2
2
2 2
1
1
tdt dt
I arctgt C
t
t t
= = = +
+
+
∫ ∫
2
arctg x C
= +
.
Цей інтеграл можна обчислити й безпосередньо.
Другий спосіб.
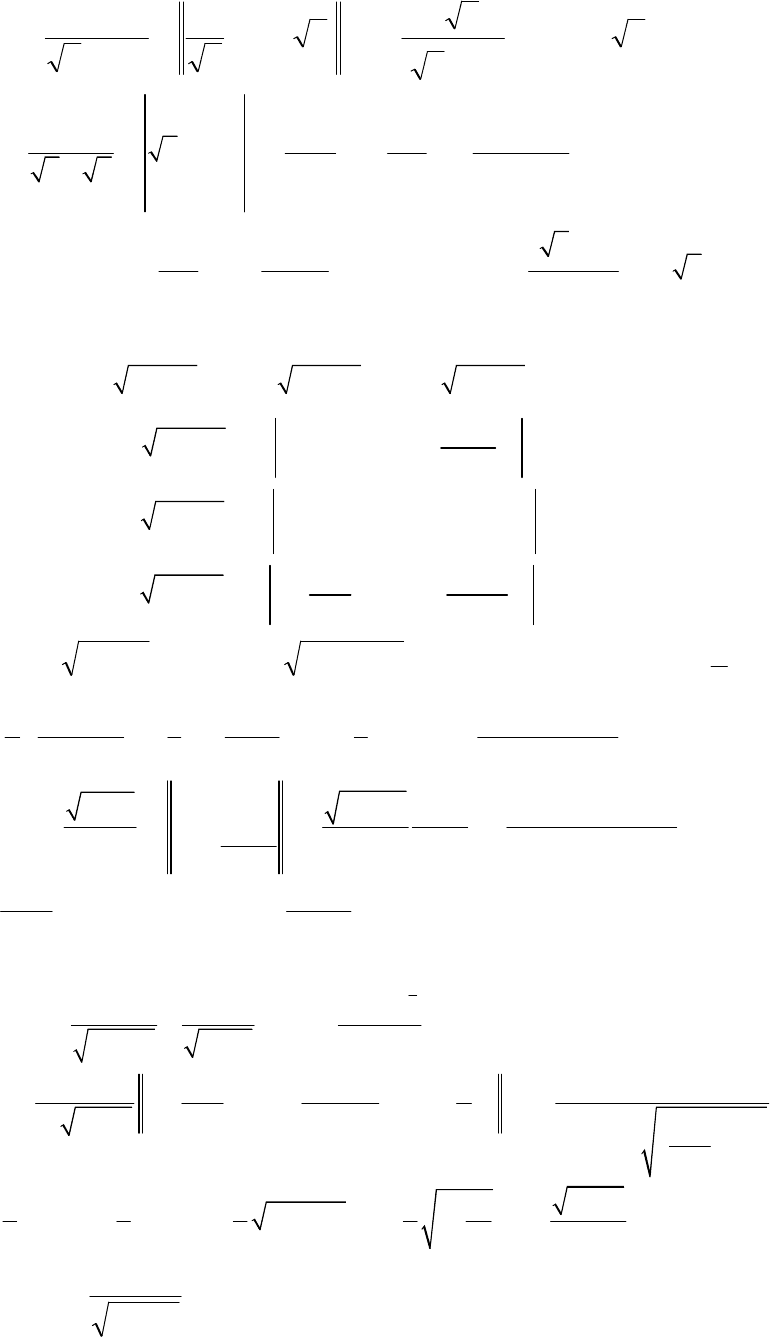
120
( )
( )
(
)
( )
Cxarctg
x
xd
xd
x
dx
xx
dx
I +=
+
===
+
=
∫∫
2
1
22
1
2
.
6.
( )
4
2
3 2
4
2
4
3
1 1
4
4 4
1 1
4
x t
t
dx t dt t dt
x t dt
t t t t
x x
dx t dt
=
− +
= = = = =
+ + +
+
=
∫ ∫ ∫ ∫
( )
( )
( )
(
)
( )
2
2 4
4
1
1
4 1 4 ln 1 4 ln 1
1 2 2
x
t
dt
t dt t C x
t
−
−
= − + = + + + = + + +
+
∫ ∫
С
При інтегруванні виразів виду:
(
)
2 2
,
R x x a
+
,
(
)
2 2
,
R x a x
−
,
(
)
2 2
,
R x x a
−
використовують заміни:
(
)
(
)
( )
2 2
2
2 2
2 2
2
) , ;
cos
sin ; cos
) ,
cos ; sin
cos
) , ; .
sin sin
a
a R x a x dx x a tgt dx dt
t
x a t dx a tdt
b R x a x dx
x a t dx a tdt
a a t
c R x x a dt x dx dt
t t
+ = ⋅ =
= =
−
= = −
− = = −
∫
∫
∫
7.
∫ ∫ ∫ ∫
===−=− tdtsintdtcostsintdtcostsintsindxxx 2
4
1
11
2222222
(
)
sin 4arcsin
1 1 cos4 1 sin 4 1
arcsin .
4 2 8 4 8 4
x
t t
dt t C x C
−
= = − + = − +
∫
8.
2
2 4
4 4 2 4 2
2
1
1 cos
cos cos sin cos
cos
x tgt
tg t
x dt tdt
I dx
dt
x tg t t t t t
dx
t
=
+
+
= = = =
⋅ ⋅
=
∫ ∫ ∫
4
4 3
cos 1
sin sin
sin 3sin
t
dt t d t c
t t
−
= = − +
∫ ∫
.
Зробимо зворотну заміну, тобто виразимо sint через
x:
3
2
2
3
2 2
(1 )
sin ;
3
1 1
tgt x x
t I c
x
tg t x
+
= = = − +
+ +
.
9.
2
2
2 2 2
2
3 3cos 3 3cos sin
, , sin
sin sin
9
3
sin 9 9
sin
dx tdt t tdt
x dx t
t t x
x x
t
t
⋅
= = − = = −
−
⋅ ⋅ −
∫ ∫
=
2
2
2
1 1 1 1 9 9
sin cos 1 sin 1
9 9 9 9 9
x
tdt t c t c c c
x x
−
− = + = − + = − + = +
∫
.
10.
∫
−
=
2
5
1 x
dxx
J
1-й спосіб (заміна змінної):
