Архіпова О.С. Вища математика
Подождите немного. Документ загружается.


11
=+++
=+++
=+++
nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
...
..........................................
...
...
2211
22222121
11212111
(1.4.)
2)
де
(
)
iij
bnjnia ,,1,,1 ==
– коефіцієнти,
i
x
– невідомі.
Системи рівнянь називаються еквівалентними, якщо будь-який розв’язок
однієї з них є розв’язком іншої.
Ввівши в розгляд матриці-стовпці
1 1
2 2
,
... ...
n n
x b
x b
X B
x b
= =
систему рівнянь можна переписати в матричному виді
B
AX
=
.
Якщо
(
)
njb
j
,1=
дорівнюють нулю, система називається однорідною,
інакше система називається неоднорідною.
1.4. 2. Правило Крамера
Нехай
,0det
≠
∆
=
A
тоді розв’язок системи рівнянь (1.4) має вигляд
( )
,,1 njx
j
j
=
∆
∆
=
де
j
∆
– визначник, отриманий із визначника
∆
системи
заміною j-го стовпця при невідомому
j
x
стовпцем правих частин В.
Якщо
0
=
∆
, а хоча б один з
,0≠∆
j
то система несумісна, тобто
розв’язків не має.
Якщо
,0...
21
=∆==∆=∆=∆
n
то система рівнянь або несумісна, або
невизначена, тобто має нескінченну множину розв’язків.
Приклад 1. Розв’язати систему рівнянь за формулами Крамера.
2 4,
3 5 3 1,
2 7 8.
x y z
x y z
x y z
+ + =
− + =
+ − =
Розв’язання.
Визначник системи
;33
172
353
121
=
−
−=∆
знаходимо
;33
872
153
421
;33
182
313
141
;33
178
351
124
321
=−=∆=
−
=∆=
−
−=∆

12
тоді
.1
33
33
,1
33
33
,1
33
33
3
3
2
2
1
1
==
∆
∆
===
∆
∆
===
∆
∆
= xxx
1.4. 3. Розв’язування систем рівнянь матричним способом (за
допомогою оберненої матриці)
Лінійна система рівнянь у матричному виді
B
AX
=
. Домножимо на
1
−
A
матричне рівняння, одержимо розв’язок
.
1
BAX
−
=
Приклад 1. Розв’язати систему рівнянь матричним способом (за
допомогою оберненої матриці):
2 4,
3 5 3 1,
2 7 8.
x y z
x y z
x y z
+ + =
− + =
+ − =
Розв’язання.
Нехай
,,
8
1
4
,
172
353
121
=
=
−
−=
z
y
x
XBA
тоді система рівнянь прийме вид
B
AX
=
й її розв’язок
.
1
BAX
−
=
Обернена матриця, обчислена раніше, дорівнює
−−
−
−
=
−
3
1
11
1
33
31
0
11
1
11
3
3
1
11
3
33
16
1
A
, звідси:
,
1
1
1
8
1
4
3
1
11
1
33
31
0
11
1
11
3
3
1
11
3
33
16
=
=
−−
−
−
=
z
y
x
X
де
16 3 1
4 1 8 1,
33 11 3
3 1
4 1 0 8 1,
11 11
31 1 1
4 1 8 1.
33 11 3
x
y
z
−
= ⋅ + ⋅ + ⋅ =
= ⋅ − ⋅ + ⋅ =
= ⋅ − ⋅ − ⋅ =
1.4.4. Системи m лінійних рівнянь із n невідомими
Теорема Кронекера - Капеллі.
Теорема 1. Для того щоб система лінійних рівнянь

13
=+++
=+++
=+++
mnmnmm
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa
...
.............................................
...
...
2211
22222121
11212111
була сумісною, необхідно й достатньо, щоб ранг розширеної матриці системи
був рівний рангу її основної матриці, тобто
(
)
(
)
.
розш
r A r A
=
Тут
11 12 1 1 11 12 1
21 22 2 2 21 22 2
.
1 2 1 2
... ...
... ...
,
... ... ... ... ... ... ... ... ...
... ...
n n
n n
ðî çø
m m mn m m m mn
a a a b a a a
a a a b a a a
A A
a a a b a a a
= =
.
Системи лінійних однорідних рівнянь
(
)
mib
i
,1;0
==
.
Система лінійних однорідних рівнянь завжди сумісна, має очевидний
нульовий (тривіальний) розв’язок
(
)
0 1
i
розш
x ; i ,n; r( A) r A= = =
, оскільки
додавання нульового стовпця не збільшує рангу матриці.
Теорема 2. Для того, щоб однорідна система лінійних рівнянь мала
ненульовий розв’язок, необхідно й достатньо, щоб ранг r матриці її
коефіцієнтів був менше числа невідомих n.
Наслідок. Будь-яка система m лінійних однорідних рівнянь, число
рівнянь у якій менше числа невідомих, має нетривіальний розв’язок.
Теорема 3. Для того, щоб однорідна система n рівнянь із n
невідомими мала ненульовий розв’язок, необхідно й достатньо, щоб її
визначник був рівний нулю.
Означення. Рядки e
1
, e
2
,…,e
m
називаються лінійно залежними, якщо
знайдуться такі числа
m
ααα
...,,,
21
, з яких хоча б одне не дорівнює нулю, що
0...
2211
=+++
mm
eee
ααα
, інакше рядки називаються лінійно незалежними.
Теорема 4(про базисний мінор). Якщо ранг матриці дорівнює r, то в
цій матриці можна знайти r лінійно незалежних рядків, через які лінійно
виражаються всі інші рядки. Зазначені r рядків називаються базисними.
1.4.5. Правило розв’язування довільної системи m лінійних рівнянь
із n невідомими
Загальним розв’язком системи лінійних рівнянь називається такий
розв’язок, у якому базисні невідомі виражені через інші невідомі, які
називаються вільними.
Частинним розв’язком називається розв’язок, отриманий із загального
розв’язку при деяких числових значеннях вільних невідомих.
Базисним розв’язком називається частинний розв’язок, вільні невідомі
якого дорівнюють нулю.

14
1. Обчислюючи ранги основної й розширеної матриці системи, з'ясовують
питання про її сумісність. Якщо система сумісна, то знаходять який-
небудь базисний мінор порядку r.
2. Береться r рівнянь, з коефіцієнтів яких складений базисний мінор; інші
рівняння відкидають. Невідомі, коефіцієнти яких входять у базисний
мінор, називають головними й залишають ліворуч, а інші n-r невідомих
називають вільними й переносять у праві частини рівнянь.
3. За правилом Крамера знаходять вирази головних невідомих через вільні.
Отримані рівності будуть загальним розв’язком системи.
4. Надаючи вільним невідомим будь-які числові значення, знаходять
відповідні значення головних невідомих. Тим самим знаходять
частинний розв’язок вихідної системи рівнянь.
Приклад 1. Знайти загальний розв’язок системи рівнянь.
1 2 3 4
1 2 3 4
1 2 3 4
2 3 5 7 1,
4 6 2 3 2,
2 3 11 15 1.
x x x x
x x x x
x x x x
− + + =
− + + =
− − − =
Розв’язання.
Досліджуємо систему на сумісність.
( )
( )
2 1 2
.
3 1 3
2 3 5 7 1 2 3 5 7 1
2
4 6 2 3 2 ~ ~ 0 0 8 11 0 ~
1
2 3 11 15 1 0 0 16 22 0
розш
a a a
A
a a a
− −
+ ⋅ − →
= − − −
+ ⋅ − →
− − − − −
( )
( )
3 2 3
2 2
2 3 5 7 1
2
~ ~ 0 0 8 11 0 ~
1
0 0 0 0 0
a a a
a a
−
+ ⋅ − →
⋅ − →
2 3 5 7 1
0 0 8 11 0
−
.
Відкидання нульового рядка не міняє рангу матриці. Оскільки мінор
2
5 7
55 56 1 0,
8 11
∆ = = − = − ≠
тобто
(
)
(
)
.
розш
r A r A=
, система сумісна.
Оскільки перетворення відносилися тільки до рядків, система рівнянь
рівносильна наступній системі:
=+
=++−
0118
17532
43
4321
xx
xxxx
Це базисна система рівнянь. Знайдемо головні невідомі
3
x
й
4
x
, виразивши їх
через вільні невідомі
1
x
й
2
x
.
=+
+−=+
0118
32175
43
2143
xx
xxxx

15
Застосуємо формули Крамера, що дає загальний розв’язок системи
1 2
3 1 2
1 2
4 1 2
3
4
3 1 2 4 1 2
5 7 1 2x 3x 7
1; 22x 33x 11;
8 11 0 11
5 1 2x 3x
16x 24x 8 ;
8 0
x 22x 33x 11; x 16x 24x 8,
− +
∆ = = − ∆ = = − + +
− +
∆ = = − −
∆
∆
= = − − = = − + +
∆ ∆
де базисні
3
x
й
4
x
невідомі виражені через вільні змінні
1
x
й
2
x
.
Отримано загальний розв’язок системи
++−
−−
=
82416
113322
21
21
2
1
xx
xx
x
x
X
Візьмемо частинний розв’язок, вважаючи
1
1
=x
,
1
2
=x
, тоді
22
3
−=x
;
16
4
=x
,
тобто
(
)
16;22;1;1 −=
T
r
X
.
Перевіримо розв’язок, підставивши частинний розв’язок у вихідну систему
рівнянь:
( )
=⋅−−⋅−−
=⋅+⋅−−
=⋅+⋅−−
11615221132
216322264
116752232
Всі рівняння системи перетворюються в тотожності. Розв’язок знайдено.
Контрольні завдання до розділу 1
Завдання 1. Обчислити визначники
1.1.1.
3242
4123
2343
2134
1.1.2.
5317
3175
1753
7531
1.1.3.
2423
4321
4213
4132 −
1.1.4.
2434
3245
4523
5342
−
−
−
1.1.5.
1012
2101
3210
4321
−−
−
1.1.6.
2104
3321
1123
3011
−
−
−
1.1.7.
1403
3234
1013
2421
−
−
−−
1.1.8.
3242
4123
2343
1334
1.1.9.
3111
1311
1131
1113
1.1.10.
201041
10631
4321
1111
1.1.11.
3214
2143
1432
4321
1.1.12.
642781
16941
4321
1111

16
1.1.13.
5432
4213
7364
4215
1.1.14.
1234
2143
3412
4321
−−
−−
−−
1.1.15.
2121
1124
1113
1112
−
−
−
1.1.16.
4322
2131
3641
1254
−
1.1.17.
1321
2112
1213
2131
−
−−
−
−−
1.1.18.
1234
2113
3212
4321
1.1.19.
1334
2343
4123
3242
1.1.20.
3121
3101
0123
2012
−
−
1.1.21.
3471
5121
1121
1121
−
−
−−
−
1.1.22.
3242
4721
4563
2321
−
−
−
−
1.1.23.
6210
2213
2121
4311
−
−−
−−
−
1.1.24.
15532
13011
8301
4321
−−
−−−
1.1.25.
3204
1523
0412
0101
−
1.1.26.
1321
3021
4301
4321
−−−
−−
−
1.1.27.
1201
4152
2363
4512
−
1.1.28.
5321
0400
2120
0471
−
1.1.29.
4121
0321
0928
7651
−
1.1.30.
5210
3002
1130
1212
−
−

17
РОЗДІЛ 2
ВЕКТОРНА АЛГЕБРА
2.1. Основні поняття
Багато фізичних величин (сила, швидкість, прискорення й ін.)
характеризуються не тільки числовим значенням, але й напрямом. Такі
величини називаються векторними.
Векторну величину геометрично зображують за допомогою відрізка
певної довжини й певного напряму.
Вектором будемо називати напрямлений відрізок (рис. 2.1). Напрям
вектора вказується стрілкою. Точка А називається початком, а точка В –
кінцем. Вектори позначаються буквами
, , ,...,
a b c
r r r
a також
AB
uuur
,
CD
uuur
,... (на
першому місці ставиться початок вектора).
Відстань між початком і кінцем вектора називається довжиною або
модулем вектора. Довжина вектора
a
r
позначається |
a
r
|.
Вектори, розташовані на одній прямій або на паралельних прямих,
називаються колінеарними.
Два вектори називаються рівними, якщо вони збігаються при
паралельному переносі. Паралельний перенос переводить початок і кінець
одного вектора відповідно в початок і кінець іншого вектора, тобто
1 1
AB AB
=
uuur uuuur
(рис. 2.2).
Два вектори називаються однаково напрямленими (протилежно
напрямленими), якщо вони колінеарні й у рівних їм векторів, що мають
загальний початок, кінці розташовуються по одну сторону від початку
(відповідно по різні сторони від початку).
Рівні вектори однаково напрямлені й мають рівні довжини. І обернено,
якщо вектори однаково напрямлені й мають рівні довжини, то вони рівні. Від
будь-якої точки можна відкласти вектор, рівний даному, і притому тільки
один.
До векторів будемо відносити й нульовий вектор, початок і кінець якого
збігаються.
A B
a
r
A
B
A
1
B
1
Рис. 2.1 Рис. 2.2
18
Нульовий вектор позначається
0
r
. Його довжина дорівнює нулю.
Нульовий вектор вважається колінеарним будь-якому вектору, тому що він
не має певного напряму. Всі нульові вектори рівні.
2.2. Лінійні операції над векторами
Означення. Сумою вектора
AB
uuur
й вектора
BC
uuur
називається вектор
AC
uuur
:
AC
uuur
=
AB
uuur
+
BC
uuur
. Сумою вектора
AB
uuur
й довільного вектора
PQ
uuur
називається
сума вектора
AB
uuur
й вектора
BC
uuur
, рівного
PQ
uuur
(рис. 2.3) (правило трикутника).
За означенням для будь-якого вектора
a
r
й нульового вектора
0
r
a
r
+
0
r
=
0
r
+
a
r
=
a
r
.
Якщо
a
r
=
1
a
r
,
b
r
=
1
b
r
то
a
r
+
b
r
=
1
a
r
+
1
b
r
. Це випливає з означення суми
векторів і рівності векторів.
Властивості додавання векторів.
1) Сполучна властивість: (
a
r
+
b
r
) +
c
r
=
a
r
+(
b
r
+
c
r
).
2) Переставна властивість:
a
r
+
b
r
=
b
r
+
a
r
.
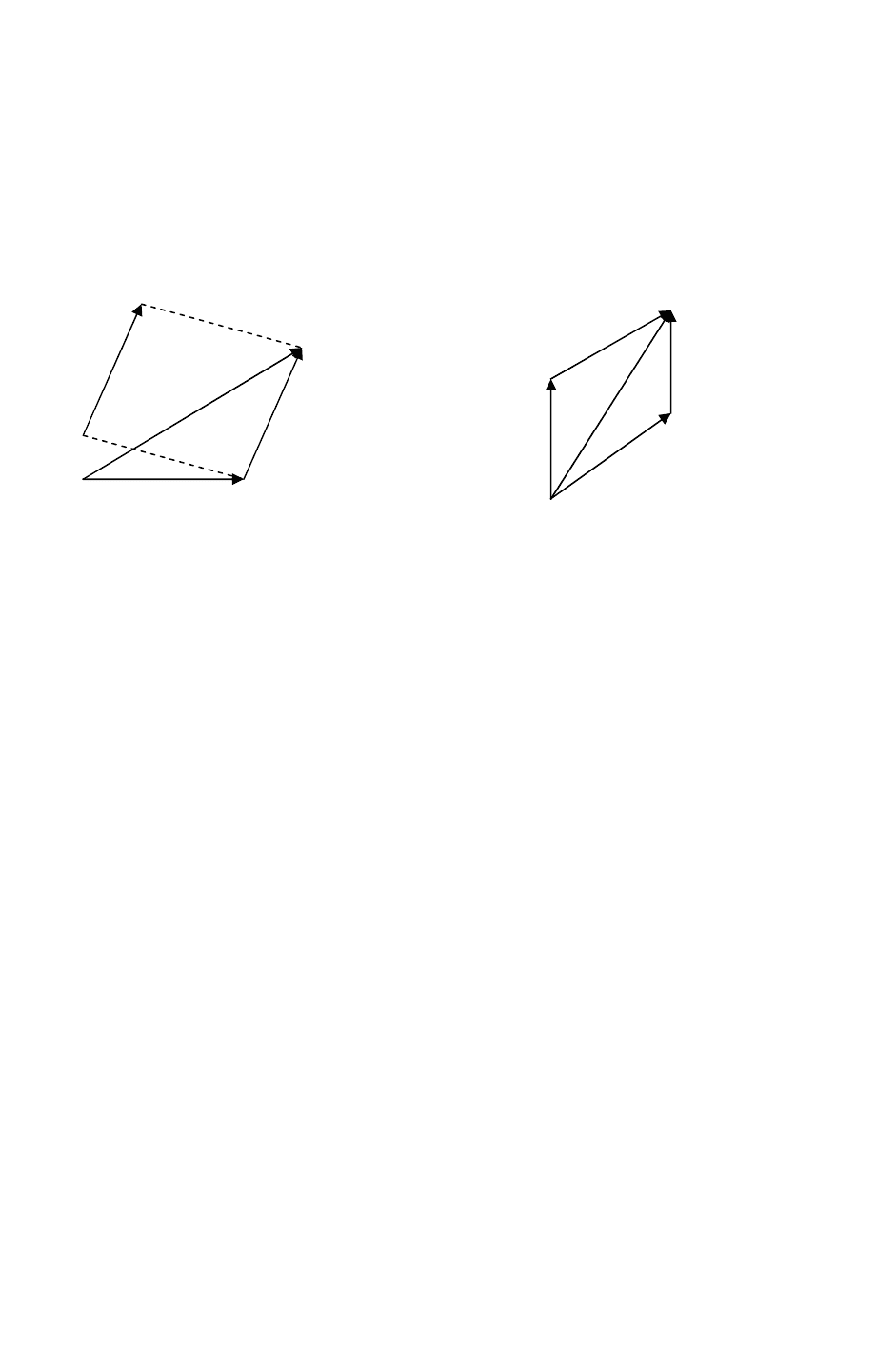
Додавання двох неколінеарних векторів
a
r
і
b
r
можна виконувати за
правилом паралелограма: вектори
a
r
й
b
r
відкладаються від однієї точки А
(рис. 2.4) і будується паралелограм зі сторонами
AB
uuur
й
AC
uuur
.Тоді
AD
uuur
=
a
r
+
b
r
. .
Правило для побудови вектора суми: «з початку одного вектора в
кінець іншого».
Вектором, протилежним вектору
AB
uuur
, називається вектор
BA
uuur
:
BA
uuur
= -
AB
uuur
.
За означенням вектор, протилежний нульовому вектору, є нульовий вектор.
Очевидно,
a
r
+ (-
a
r
) =
0
r
.
Різницею векторів
a
r
й
b
r
(позначається
a
r
-
b
r
) називається сума вектора
a
r
й вектора -
b
r
, протилежного
b
r
:
a
r
-
b
r
=
a
r
+( -
b
r
).
Кутом між ненульовими векторами
AB
uuur
й
AC
uuur
називається кут ВАС.
Кутом між будь-якими двома векторами
a
r
й
b
r
називається кут між
рівними їм векторами із загальним початком. Кут між однаково
напрямленими векторами вважається рівним нулю.
Таким чином, якщо φ – градусна міра кута між векторами
a
r
й
b
r
, 0
0
≤φ≤ 180
0
.
Означення. Добутком ненульового вектора
a
r
на дійсне число λ ≠ 0
називається вектор, довжина якого дорівнює добутку довжини вектора
a
r
A
B
C
D
b
r
a
r
c a b
= +
r r r
c
r
Рис. 2.4
A
B
C
P
Q
Рис. 2.3

19
на модуль числа λ, а напрям збігається з напрямом вектора
a
r
при λ > 0 і
протилежно напряму
a
r
при λ < 0.
Добуток вектора
a
r
на число λ позначається λ
a
r
(числовий множник
пишеться ліворуч). За означенням
|
a
λ
r
| =|
λ
|.|
a
r
|.
Якщо вектор
a
r
– нульовий або число λ дорівнює нулю, то покладають
λ·
0
r
=
0
r
для будь-якого числа λ,
0·
a
r
=
0
r
для будь-якого вектора
a
r
.
Властивості множення вектора на число.
1) Сполучна властивість: (λµ)
a
r
= λ( µ
a
r
).
2) Перша розподільна властивість: λ
a
r
+ µ
a
r
= (λ+µ)
a
r
.
3) Друга розподільна властивість: λ
a
r
+λ
b
r
= λ(
a
r
+
b
r
).
Теорема. Ненульові вектори
a
r
й
b
r
колінеарні тоді й тільки тоді, коли
існує таке число λ, що
b
r
=λ
a
r
.
2.3. Координати вектора
Вектор, довжина якого прийнята за одиницю виміру довжини, називають
одиничним. Позначимо через
i
r
,
j
r
,
k
r
одиничні вектори, відкладені від точки
О в додатних напрямах на осях Ох, Оу,Oz прямокутної системи координат.
Одиничні вектори
i
r
,
j
r
,
k
r
, де
i j k
⊥ ⊥
r r r
й (
i
r
=
j
r
=
k
r
= 1), що мають
напрями додатних координатних півосей, називаються координатними
векторами або ортами.
Теорема 1 (про розкладання вектора по осях координат).
Кожен вектор
a
r
можна представити у вигляді:
(2.3.1)
і притім єдиним чином.
Z
Y
X
O
i
r
M
B
M
1
A
i
r
k
r
r
C
j
r
Рис. 2.5
x y z
a a i a j a k
= + +
r r r r

20
Якщо вектор
a
r
представлений у вигляді (2.3. 1), то говорять, що вектор
a
r
розкладений по векторах
i
r
,
j
r
,
k
r
. Вектори a
x
i
r
, a
y
j
r
і
z
a k
r
називають
складовими вектора
a
r
по осях Ох , Оу й Oz . Коефіцієнти a
x
, a
y
, a
z
–
розкладання вектора
a
r
по одиничних векторах
i
r
,
j
r
і
k
r
називають
координатами вектора
a
r
в даній системі координат Оху й записують
a
r
(a
x
;
a
y
; a
z
) . Тоді
2 2 2
x y z
a a a a
= + +
r
.
З єдиності розкладання випливає, що рівні вектори мають рівні
відповідні координати, і, обернено, якщо у векторів відповідні координати
рівні, то вектори рівні.
Нехай дана точка М(х; y;z). (рис.2.5) Тоді
,
r OM xi y j zk
= = + +
r uuuur r r r
-це радіус-вектор точки М (2.3. 2)
де х, у, z – координати точки М, тобто
2 2 2
( , , ), , (1,0,0), (0,1,0), (0,0,1)
r r x y z r x y z i j k= = + + = = =
r r r r r r
.
Формула (2.3.2) представляє собою розкладання вектора
OM
uuuur
по векторах
i
r
,
j
r
,
k
r
. Числа x, y, z , що є проекціями вектора
OM
uuuur
, називаються
координатами вектора
r
r
:
,
ох
x
пр
r
=
r
,
о
y
y
пр r
=
r
,
о
z
z
пр
r
=
r
Теорема 2. Кожна координата суми векторів
1 2 3
a a i a j a k
= + +
r r r r
і
1 2 3
b b i b j b k
= + +
r r r r
дорівнює сумі відповідних координат цих векторів; кожна
координата добутку вектора
a
r
на число λ дорівнює добутку відповідної
координати цього вектора на число λ.
c
r
=λ
a
r
+µ
b
r
↔
1 1 2 2 3 3
( ) ( ) ( )
c a b i a b j a b k
λ µ λ µ λ µ
= + + + + +
r r r r
Теорема 3. У колінеарних векторів відповідні координати пропорційні.
І обернено, якщо у двох векторів відповідні координати пропорційні, то
вектори колінеарні.
a
r
׀׀
b
r
↔
b
r
=λ
a
r
↔
3
1 2
1 2 3
b
b b
a a a
λ
= = =
.
Якщо λ>0,
a
r
↑↑
b
r
– вектори однаково напрямлені; якщо λ<0,
a
r
↑↓
b
r
–
вектори протилежно напрямлені.
З
означення колінеарних векторів випливає, що два вектори колінеарні в
тім і тільки тім випадку, якщо один з них може бути отриманий множенням
іншого на деяке число λ, тобто
a b
λ
=
r
r
. (2.3. 3)
Нехай вектори
a
r
й
b
r
задані своїми координатами, тобто
(
)
1 1 1
, ,
a x y z
=
r
,
(
)
2 2 2
, ,
b x y z
=
r
, тоді векторна рівність (2.3. 3) еквівалентна трьом числовим:
1 2 1 2 1 2
, ,
x x y y z z
λ λ λ
= = =
,
з яких випливає
1 1 1
2 2 2
x y z
x y z
= =
. (2.3. 4)
Таким чином, вектори колінеарні, якщо їхні координати пропорційні.
