Архіпова О.С. Вища математика
Подождите немного. Документ загружается.

131
( )
( )
∫ ∫ ∫ ∫
⋅+
⋅+
+
+⋅
−
;dx
x
xlnarctg
.4;dxe4x3.3;dx
xsin2x
xcosx
.2;dx
1xx
x1
.1
x3
2
( ) ( )
∫ ∫ ∫
+⋅+
+++
−−+
+
;dx
2x1x
7x11x6x
.7;dx
x9
x
.6;dx
5x6x9
4x3
.5
3
23
2
2
2
(
)
( )
∫ ∫ ∫
+
+⋅+⋅
−⋅+
.dxe1e.10;dx
12xcos11xsin3
1
.9;dx
1x4x
1
.8
xx2
2
6.1.6.
(
)
( )
(
)
∫ ∫ ∫
+
⋅−⋅
⋅+⋅
−
−
;dx4xln.3;dx
xcos3xsin2
xsin3xcos2
.2;dx
x1
1xarccos
.1
2
3
2
3
( ) ( )
∫ ∫ ∫∫
−⋅+
−+−−
+−
−
⋅
−
;dx
2x2x
10x11x6x
.7;dx
x
1x
.6;dx
2xx
x41
.5;dxex.4
3
23
4
2
2
x3
2
( )
(
)
( )
∫ ∫∫
−
+
−
+−⋅
+⋅+
.dx
x1
x1
2x.10;dx
17xsinxcos18
1
.9;dx
1x1x
1
.8
2
6.1.7.
( )
∫ ∫ ∫ ∫
⋅
⋅−
+
−
⋅ ;dx
x
cos
xsinx
.4;dxex61.3;dx
x
4
1
x2arctgx8
.2;xdxcoslnxtg.1
3
x2
2
( )
( ) ( )
∫ ∫ ∫
+⋅−
+++
−
+−
−
;dx
1x1x
1x7x6x2
.7;dx
x1
x
.6;dx
1x8x4
x52
.5
3
22
3
2
4
2
( )
( )
∫ ∫ ∫
+
++
++
.xdx2cosx2sinxcos1.10;dx
9xsinxcos8
1
.9;dx
2x1x
1
.8
2
2
6.1.8.
( )
( )
( )
( )
( )
∫ ∫ ∫ ∫
⋅−
+
+
+
;dx
x
x
1
arctg
.4;xdx2cos2x4.3;dx
xx
x21
.2;dx
1xcos
1xtg
.1
222
( )
( ) ( )
∫ ∫ ∫
+⋅−
+++
−
+−−
−
;dx
2x1x
10x10x6x
.7;dx
x4
1
.6;dx
3x2x
1x4
.5
3
23
3
2
2
∫ ∫ ∫
−
+⋅−⋅
−
.dx1e.10;dx
7xsin5xcos5
1
.9;dx
x16
1
.8
x
4
6.1.9.
( )
( )
∫ ∫ ∫ ∫
⋅−
⋅
+
+
;dx
x
xarccos
.4;xdx2sinx42.3;dx
ecos
ex
.2;dx
1x
xx
.1
2
2
x2
x
2
2
3
(
)
( )
∫ ∫ ∫
+⋅
+++
−
+−
−
;dx
1xx
2x7x6x2
.7;dx
x4
x
.6;dx
4x4x2
3x5
.5
3
23
23
2
4
2
( )
( )
∫ ∫ ∫
⋅+⋅+⋅
+⋅+⋅
.dx
xcosxsin
xtgln
.10;dx
23xsin2xcos25
1
.9;dx
1x1xx
1
.8
2
6.1.10.
132
( )
∫ ∫ ∫ ∫
⋅⋅−
+−
−
;xdxcoslnxsin.4;dxe2x5.3;dx
1x
x
.2;dx
)xsinx(
xcos1
.1
x3
42
( )
∫ ∫ ∫
−⋅
−+−
−++−
+
;dx
2xx
8x13x6x
.7;dx
x16
x
.6;dx
4xx
2x3
.5
3
23
2
2
2
( )
( )
(
)
∫ ∫∫
−
+⋅+⋅
+⋅−
.dx
4x
x
.10;dx
3xsin3xcos5
1
.9;dx
1x1x
1
.8
2
2
5
2
6.1.11.
∫ ∫ ∫ ∫
−
−
−
+
−
;dxxarcsinx.4;dx1x6arctg.3;dx
x1
1x
.2;dx
)xsinx(cos
xcosxsin
.1
23
2
5
( ) ( )
∫ ∫∫
−⋅+
−+−
−
−+
+
;dx
2x1x
7x13x6x
.7;dxx4.6;dx
2x4x4
4x2
.5
3
23
2
2
(
)
∫ ∫ ∫
+
−
+⋅−⋅
⋅+
.dx
x1
x1
.10;dx
1xsin3xcos2
1
.9;dx
x2x
1
.8
2
6.1.12.
( )
( )
∫ ∫ ∫ ∫
−
+
+
⋅
+
⋅
−
;dx
x
xlnarcctg
.4;dx3x4e.3;dx
x1
xxarctg
.2;dx
xsinx
xsinxcosx
.1
x2
22
(
)
( ) ( )
∫ ∫ ∫
−⋅+
−+−
+
−+−
+−
;dx
2x1x
6x14x6x
.7;dx
x16
1
.6;dx
1x3x
1x3
.5
3
23
23
2
2
( )
(
)
∫ ∫ ∫
+−⋅
⋅+⋅−
.dx
xsin
xcos
.10;dx
5xsinxcos7
1
.9;dx
x2xx1
1
.8
8
2
2
6.1.13.
(
)
∫ ∫ ∫ ∫
⋅
+
−
+
+
;dxex4sin.4;dx
x
cos
x
.3;dx
x
1
xarctgx
.2;dx
1
x
xx
.1
x2cos
22
4
4
3
( ) ( )
∫ ∫ ∫
−⋅+
−+−
−
−−
+−
;dx
2x1x
10x10x6x
.7;dxx16x.6;dx
7x2x6
6x3
.5
3
23
22
2
( )
(
)
∫ ∫ ∫
+
−
+⋅+⋅
+⋅+
.dx
xtg1
xtg1
.10;dx
13xsin8xcos11
1
.9;dx
1x1x
x
.8
2
6.1.14.
(
)
( )
∫ ∫ ∫∫
−
⋅
−
−
+
;dxx2sinlnx4sin.4;dx1x2arctg.3;dx
xcosx
xsinxxcos
.2;dx
x1x
x1
.1
3
( )
∫ ∫ ∫
⋅+
++
−−−−
−
;dx
x2x
2xx
.7;dx
x25
x
.6;dx
2x3x
2x3
.5
3
3
2
2
2
(
)
∫ ∫ ∫
+
+⋅+
+⋅
.dx
xsin
xcos1
.10;dx
2xsin2xcos
1
.9;dx
2xx
x
.8
22
6.1.15.
( )
( )
∫ ∫ ∫ ∫
+
−
+
−
;dx
x
x
1
arcctg
.4;dx1x4ln.3;dx
x1
1xarcsin
.2;dx
1x
x
.1
2
2
2
2
3
133
( ) ( )
∫ ∫ ∫
+⋅−
+++
−
++
−
;dx
1x1x
2x10x9x3
.7;dxx25x.6;dx
3x8x
x4
.5
3
23
22
2
( )
( )
∫ ∫ ∫
−+
++
⋅
−⋅−⋅
+⋅−
.dx
11x
11x
x.10;dx
17xcos19xsin7
1
.9;dx
4x1x
x
.8
2
6.1.16.
(
)
( )
( )
∫ ∫ ∫
⋅+
+⋅
−
−
−+
;xdx2cos6x5.3;dx
1xx
x1
.2;dx
1x
1xln1
.1
( )
∫ ∫ ∫∫
⋅+
++
−
+−−
−
;dx
x1x
1xx2
.7;dxx16.6;dx
5xx
4x3
.5;dxearcsine.4
3
3
2
2
xx2
( )
(
)
∫ ∫ ∫
+−⋅−
+⋅−
.dx
xsin1
xsin
.10;dx
1xcos3xsin
1
.9;dx
1x2x
1
.8
2
6.1.17.
(
)
(
)
( )
∫ ∫ ∫
−
+
++
+
;xdx4cos5x2.3;dx
xtg1xcos
1
.2;dx
1x3x
1x
.1
25
3
2
( )
∫ ∫∫
−
−−
−
;dx
x16
1
.6;dx
8x2x
x1
.5;dx
x
xarctg
.4
3
2
2
( ) ( )
( )
∫ ∫ ∫∫
−
++
+
+⋅+
+++
.dxxax.10;dx
xsinxcos2
1
.9;dx
x1x
1
.8;dx
1x2x
4x7x6x2
.7
23
23
6.1.18.
∫ ∫ ∫ ∫
⋅⋅−
+
+
−
;xdxsinlnxcos.4;xdx5cos)2x3(.3;dx
x
xln1
.2;dx
x
1
xxarctg
.1
2
( ) ( )
∫ ∫ ∫
+⋅+
++−
++−
+
;dx
1x2x
x5x6x2
.7;dx
x
x4
.6;dx
1x2x
5x2
.5
3
23
4
2
2
∫ ∫ ∫
⋅+⋅−⋅−
−
.dx
xcosxsin1
x2cos
.10;dx
xsin12xcos35
1
.9;dx
1x
1
.8
4
6.1.19.
( )
∫ ∫ ∫ ∫
⋅−⋅
−
+
;dx
x
xlnarcsin
.4;xdx2cos32x.3;dx
x
cos
xsinxsin
.2;dx
4
x
x
.1
4
2
2
3
(
)
( ) ( )
∫ ∫ ∫
+⋅−
++
−⋅−++
+
;dx
1x2x
x7x6x2
.7;dx
x16x16
x
.6;dx
1x12x4
3x
.5
3
23
22
4
2
(
)
(
)
∫ ∫ ∫
⋅−⋅−
+⋅+
.dx
xcos
xsin
.10;dx
xcos2xsin46
1
.9;dx
1xxx
1
.8
3
22
6.1.20.
( )
∫ ∫ ∫ ∫
⋅
⋅+
+
⋅+
+
;dx
xsin
xcosx
.4;xdx3cos7x4.3;dx
x
xlnx
.2;dx
xsin2x
xcosx
.1
2
22
2
( ) ( )
∫ ∫ ∫
+⋅−
+++
−
+−−
+
;dx
1x2x
4x5x6x2
.7;dxx9x.6;dx
4x3x
3x2
.5
3
23
22
2
134
(
)
( )
∫ ∫ ∫
−
+
+⋅+⋅
+⋅+
.dx
xsin1
xsin1
.10;dx
2xcos3xsin2
1
.9;dx
1x1x
1
.8
2
6.1.21.
( )
∫ ∫ ∫ ∫
⋅
−
+
;dxx)x(sin.4;dx
xsin
x
.3;dx
x2
ecose
.2;dx
xcos3xsin2
xsin3xcos2
.1
32
2
xx
3
( )
( ) ( )
∫ ∫ ∫
+⋅−
+++
+
++
−
;dx
2x2x
24x4x6x
.7;dx
x1
1
.6;dx
9xx
x51
.5
3
23
3
2
2
( )
( )
∫ ∫ ∫
−+
+⋅−
+⋅−
.dx
1xx
1
.10;dx
xcosxsin22
1
.9;dx
4x1x
1
.8
2
2
2
6.1.22.
(
)
( )
∫ ∫ ∫ ∫
⋅−
+
+
−
;dx
x
x
1
arccos
.4;xdx5cosx38.3;dx
1x
x
.2;dx
x41
x2arctgx8
.1
23
2
3
2
( )
( ) ( )
∫ ∫ ∫
+⋅−
+++
−
+−−
−
;dx
2x2x
4x14x6x
.7;dx
x16
1
.6;dx
4x3x
x21
.5
3
23
3
2
2
( )
( )
( )
∫ ∫ ∫
+⋅+
+⋅−⋅
+⋅+
.dx
x1x2
1
.10;dx
13xsin3xcos12
1
.9;dx
1x2x
1
.8
2
6.1.23.
(
)
( )
∫ ∫ ∫ ∫
−⋅
+
+
;dxearctge.4;dx1x5arctg.3;xdxcoslnxtg.2;dx
xx
1x21
.1
xx2
2
( )
( ) ( )
∫ ∫ ∫
+⋅−
−++
−
++
+
;dx
2x2x
4x18x6x
.7;dx
x1
x
.6;dx
24x12x6
2x3
.5
3
23
3
2
4
2
∫ ∫ ∫
+⋅
+⋅+⋅
−
.dxx3x.10;dx
3xcos4xsin3
1
.9;dx
16x
1
.8
4
6.1.24.
(
)
( )
( )
∫ ∫ ∫ ∫
⋅⋅−
+
+
+
+
;dxex4sin.4;xdx2sinx32.3;dx
1xcos
1xtg
.2;dx
1x
xx
.1
x2sin
24
3
( ) ( )
∫ ∫ ∫
+⋅−
+++−
−+−
−
.dx
2x2x
12x10x6x
.7;dx
x
x9
.6;dx
6x10x
x23
.5
3
23
4
2
2
( )
( )
∫ ∫ ∫
⋅+−
+⋅⋅+
.dx
xcosxsin
xctg
.10;dx
xcos18xsin19
1
.9;dx
1xx1x
1
.8
3
2
6.1.25.
(
)
( )
∫ ∫ ∫
⋅+
−
−
−
+ ;xdx5sin3x4.3;dx
x1
1xarccos
.2;dx
x1
1
x
xln
x
1
.1
2
3
( ) ( )
∫ ∫ ∫ ∫
−⋅+
−+−
−
++
+
;dx
2x2x
4x14x6x
.7;dxx4.6;dx
3x8x4
6x4
.5;dx
x
xarcctg
.4
3
23
2
2
135
(
)
( )
∫ ∫ ∫
−
+
+⋅+⋅
−⋅+
.dx
1xtg
1xtg
.10;dx
1xcos3xsin2
1
.9;dx
1x1x
1
.8
2
6.1.26.
( )
( )
∫ ∫ ∫ ∫
−
−
−
+
+ ;dx
x
xlnarccos
.4;xdx4sin10x7.3;dx
xsinx
xcos1
.2;dx
x1
x1
x
e
.1
2
x
( ) ( )
∫ ∫ ∫
+⋅−
+++−
−+−
−
;dx
2x2x
2x15x6x
.7;dx
x
x4
.6;dx
5x6x
x25
.5
3
23
4
2
2
(
)
∫ ∫ ∫
+⋅+⋅
+⋅
.dx
xcos
xsin
.10;dx
3xsin3xcos5
1
.9;dx
2xx
1
.8
8
2
2
6.1.27.
( )
(
)
∫ ∫ ∫ ∫
−
+
−
+
+
;dxxe.4;xdx3sinx82.3;dx
xsinxcos
xcosxsin
.2;dx
x1
xxarctg
.1
3x2
52
2
(
)
( ) ( )
∫ ∫ ∫
−⋅−
−+−
+⋅+++
+
;dx
1x2x
4x7x6x2
.7;dx
x4x4
1
.6;dx
8x6x
2x3
.5
3
23
222
( )
( )
( )
∫ ∫ ∫
+
−
+
+⋅+⋅
−+⋅
.dx
x1
x1
3x.10;dx
13xcos11xsin8
1
.9;dx
1x2xx
1
.8
2
6.1.28.
(
)
( )
( )
∫ ∫ ∫ ∫
−
⋅
+
+
−
−
;dxxarccosx.4;dxx92e.3;dx
xsinx
xsinxcosx
.2;dx
x1
arctgxx
.1
23x3
22
4
(
)
( ) ( )
∫ ∫ ∫
−⋅+
+−
−
−+−
+
;dx
1x2x
x7x6x2
.7;dx
x4
x
.6;dx
1x6x
x3
.5
3
23
23
2
4
2
( )
( )
∫ ∫ ∫
−−
−⋅+
+⋅+
.dx
1xx
1
.10;dx
xsinxcos1817
1
.9;dx
1x1x
x
.8
2
2
2
6.1.29.
∫ ∫ ∫ ∫
⋅−
+
+
+
;dxxsinx.4;dx1x3arctg.3;dx
x
sin
xcosxcos
.2;dx
1
x
xx
.1
23
4
2
4
3
(
)
( ) ( )
∫ ∫ ∫
+⋅−
+−+
−⋅−++
−
;dx
2x2x
52x10x6x
.7;dx
x1x1
1
.6;dx
1x6x
3x2
.5
3
23
222
( )
( )
∫ ∫ ∫
−⋅−⋅
⋅+
.dx
xcos
xsin
.10;dx
17xcos19xsin7
1
.9;dx
x2x
x
.8
25
3
22
6.1.30.
(
)
∫ ∫ ∫ ∫
⋅⋅
−
−
−
;xdxsinlnxcos.4;xdxsinx.3;dx
1x
x
.2;dx
x1
1xarcsin
.1
2
3
2
2
( ) ( )
∫ ∫ ∫
−⋅+
−+−
−++−
−
;dx
2x2x
6x13x6x
.7;dx
x4
x
.6;dx
1x10x
5x
.5
3
23
2
2
2
(
)
( )
∫ ∫ ∫
+
−
⋅++
−⋅+
.dx
xsin1
xsin1
.10;dx
xcos8xsin9
1
.9;dx
1x4x
x
.8
2
136
РОЗДІЛ 7
ВИЗНАЧЕНИЙ ІНТЕГРАЛ
7.1. Означення, властивості, геометричний зміст визначеного
інтеграла
До поняття визначеного інтеграла приводять задачі обчислення площ,
об'ємів тіл, довжини дуги кривої, фізичні задачі.
Нехай на відрізку
[
]
b,a визначена функція y=f(x). Розіб'ємо відрізок на
n частин точками
0 1 1i i n
a x x x x x b
−
= < < < < < < =
L L
.
На кожному з відрізків
[
]
1
,
i i
x x
−
візьмемо довільну точку
i
ξ
й складемо
суму
( )
1
n
n i i
i
S f x
ξ
=
= ∆
∑
, що називається інтегральною сумою.
Якщо існує скінченна границя інтегральної суми S
n
при
{
}
1
max 0
i
i n
x
λ
≤ ≤
= ∆ →
, що не залежить від способу розбивки області на елементарні
ділянки й вибору точок
ξ
i
, то вона називається визначеним інтегралом
функції f(x) на відрізку
[
]
,
a b
й позначається
( ) ( )
∑
∫
=
→
∆=
n
i
ii
b
a
xflimdxxf
1
0
ξ
λ
.
Функція f(x) у цьому випадку називається інтегровною на відрізку
[
]
,
a b
.
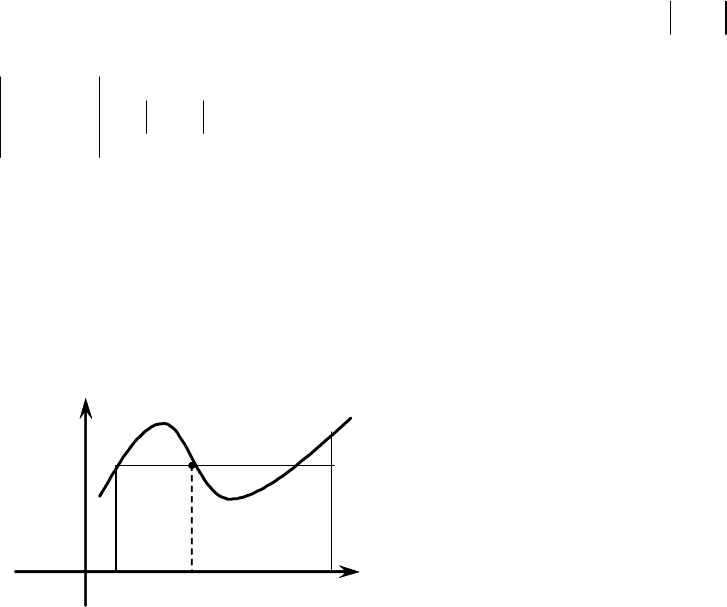
Геометричний зміст
визначеного інтеграла:
якщо
(
)
0
f x
≥
[ , ]
x a b
∀ ∈
, то
( )
b
a
f x dx
∫
чисельно
дорівнює площі
криволінійної трапеції з
основою [a,b], обмеженої
прямими x=a, x=b і
кривою y=f(x) (рис. 7.1).
Властивості визначеного інтеграла.
1.
( ) ( )
b a
a b
f x dx f x dx
= −
∫ ∫
.
2.
( ) 0
a
a
f x dx
=
∫
.
3.
Лінійність інтеграла. Якщо
(
)
f x
й
(
)
g x
– функції, інтегровні на
[
]
,
a b
, то
S
y=f(x)
a
b
y
x
Рис. 7.1
137
а)
( ) ( ) ( )
,
b b
a a
cf x dx c f x dx c const
= =
∫ ∫
; б)
( ) ( )( ) ( ) ( )
.dxxgdxxfdxxgxf
b
a
b
a
b
a
∫∫∫
±=±
Поєднуючи властивості а) і б), можна записати властивість лінійності
визначеного інтеграла:
( ) ( )
( )
( ) ( )
1 2 1 2
.
b b b
a a a
c f x c g x dx c f x dx c g x dx
+ = +
∫ ∫ ∫
4.
Адитивность інтеграла. Якщо
(
)
f x
– функція інтегровна на
[
]
,
a c
й
[
]
,
c b
, де
(
)
,
c a b
∈
, то вона інтегровна на [a,b] й
∫ ∫ ∫
+=
b
a
c
a
b
c
.dx)x(fdx)x(fdx)x(f
5. Якщо
a b
<
й
(
)
0
f x
≥
, те
( )
0
b
a
f x dx
≥
∫
, причому рівність нулю можлива
тільки в тому випадку, коли
(
)
0
f x
≡
,
(
)
b,ax
∈
∀
.
6.
Якщо
a b
<
й
(
)
(
)
f x g x
≥
, то
( ) ( )
b b
a a
f x dx g x dx
≥
∫ ∫
– теорема про
інтегрування нерівностей.
7.
Якщо
(
)
f x
– функція, інтегровна на [a,b], то
(
)
f x
– інтегровна на
[a,b] і справедлива нерівність:
( ) ( )
∫∫
≤
b
a
b
a
dxxfdxxf – теорема про модуль визначеного інтеграла.
8. Теорема про оцінку визначеного інтеграла. Якщо
(
)
m f x M
≤ ≤
, m–
найменше, М – найбільше значення функції f(x) на відрізку [a; b],то
( ) ( ) ( ).
в
а
m
в а f x dx М в а
− ≤ ≤ −
∫
9.
Теорема про середнє значення. Якщо
(
)
f x
неперервна
[
]
,
x a b
∀ ∈
, то
(
)
,
a b
ξ
∃ ∈
, що
( ) ( )( )
abfdxxf
b
a
−=
∫
ξ
.
Геометричний зміст теореми:
нехай
(
)
0
f x
≥
[ , ]
x a b
∀ ∈
, тоді існує
принаймні одна точка
(
)
,
a b
ξ
∈
, що
площа криволінійної трапеції,
обмеженої зверху неперервною
кривою
)
x
(
f
y
=
буде рівна площі
прямокутника з тією ж основою й
висотою, рівною
(
)
f
ξ
(рис. 7.2). Значення
(
)
f
ξ
називається середнім
значенням функції на відрізку [a, b].
10.
Якщо функції
(
)
xf й
(
)
x
ϕ
– неперервні на [a, b], а
(
)
x
ϕ
зберігає
знак на цьому відрізку, то (узагальнена теорема про середнє):
y
a
ξ
b x
Рис
. 7.2
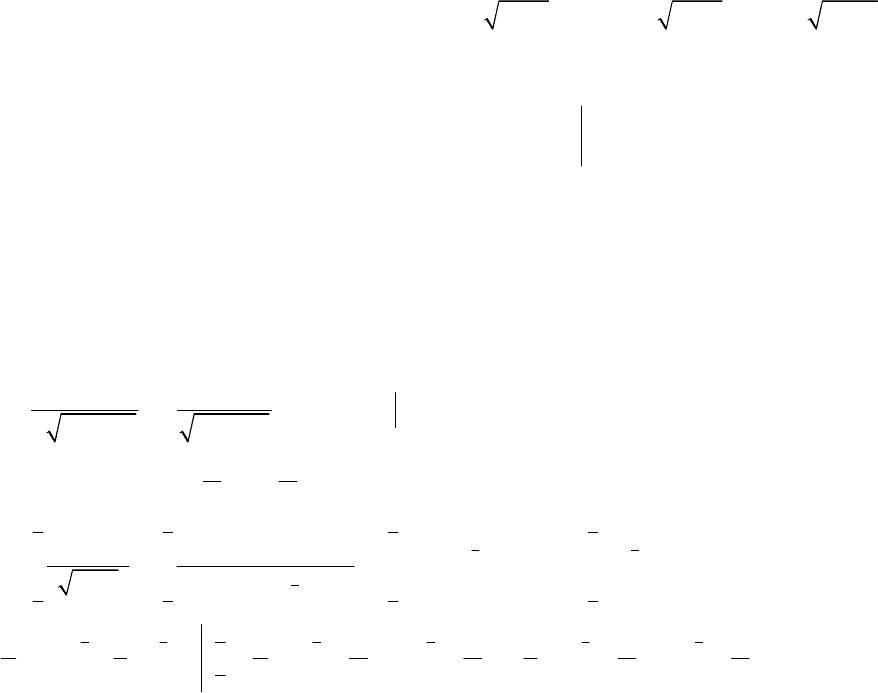
138
( ) ( ) ( ) ( )
,
b b
a a
f x x dx f x dx a b
ξ ξ
ϕ = ϕ < <
∫ ∫
11. Якщо неперервна функція
(
)
xf ,
[
]
llx ,
−
∈
– парна, то
( ) ( )
∫∫
=
−
l
0
l
l
dxxf2dxxf .
Якщо
(
)
xf – непарна, то
( )
0=
∫
−
l
l
dxxf .
7.2. Методи обчислення визначеного інтеграла
Фундаментальним результатом математичного аналізу й поворотним
моментом у розвитку інтегрального числення з'явилося відкриття зв'язку між
визначеним і невизначеним інтегралами. Це дозволило визначені інтеграли
обчислювати не як границі інтегральних сум, а через невизначені інтеграли.
Теорема. Похідна визначеного інтеграла від неперервної
функції по його верхній межі існує й дорівнює значенню
підінтегральної функції у верхній межі, тобто
( ) ( )
x
a
x
f t dt f x
′
=
∫
.
Наприклад, а)
2 2
0
x
t x
x
e dt e
− −
′
=
∫
; б)
0
3
sin
x
x
tdt
′
∫
=
3 3
0
sin sin
x
x
tdt x
′
− = −
∫
.
Формула Ньютона-Лейбніца:
( ) ( ) ( ) ( )
aFbF
a
b
xFdxxf
b
a
−==
∫
– основна
формула інтегрального числення, що встановлює зв'язок між визначеним і
невизначеним інтегралами й дозволяє знаходити значення визначеного
інтеграла як різницю значень первісної на верхній і нижній межах
визначеного інтеграла.
Приклади.
Обчислити визначені інтеграли:
1.
1
2 2
1 1
(ln )
arcsinln arcsinln arcsinln1
1 ln 1 ln
arcsin1 arcsin0 0 .
2 2
e e
e
dx d x
x e
x x x
π π
= = = − =
− −
− = − =
∫ ∫
2.
1 5
3 2
4 4 4 4
3 3
1
3
3
2 2 2 2
cos (1 sin ) (sin )
(sin ) (sin ) sin (sin )
sin
(sin )
xdx x d x
x d x xd x
x
x
π π π π
π π π π
− − − −
−
− − − −
−
= = −
∫ ∫ ∫ ∫
=
2 8 2 2 8 8
3 3 3 3 3 3
4
2
3 3 3 3
(sin ) sin sin ( ) sin ( ) sin ( ) sin ( )
2 8 2 4 2 8 4 2
x x
π
π
π π π π
−
−
− = − − − − − − −
=
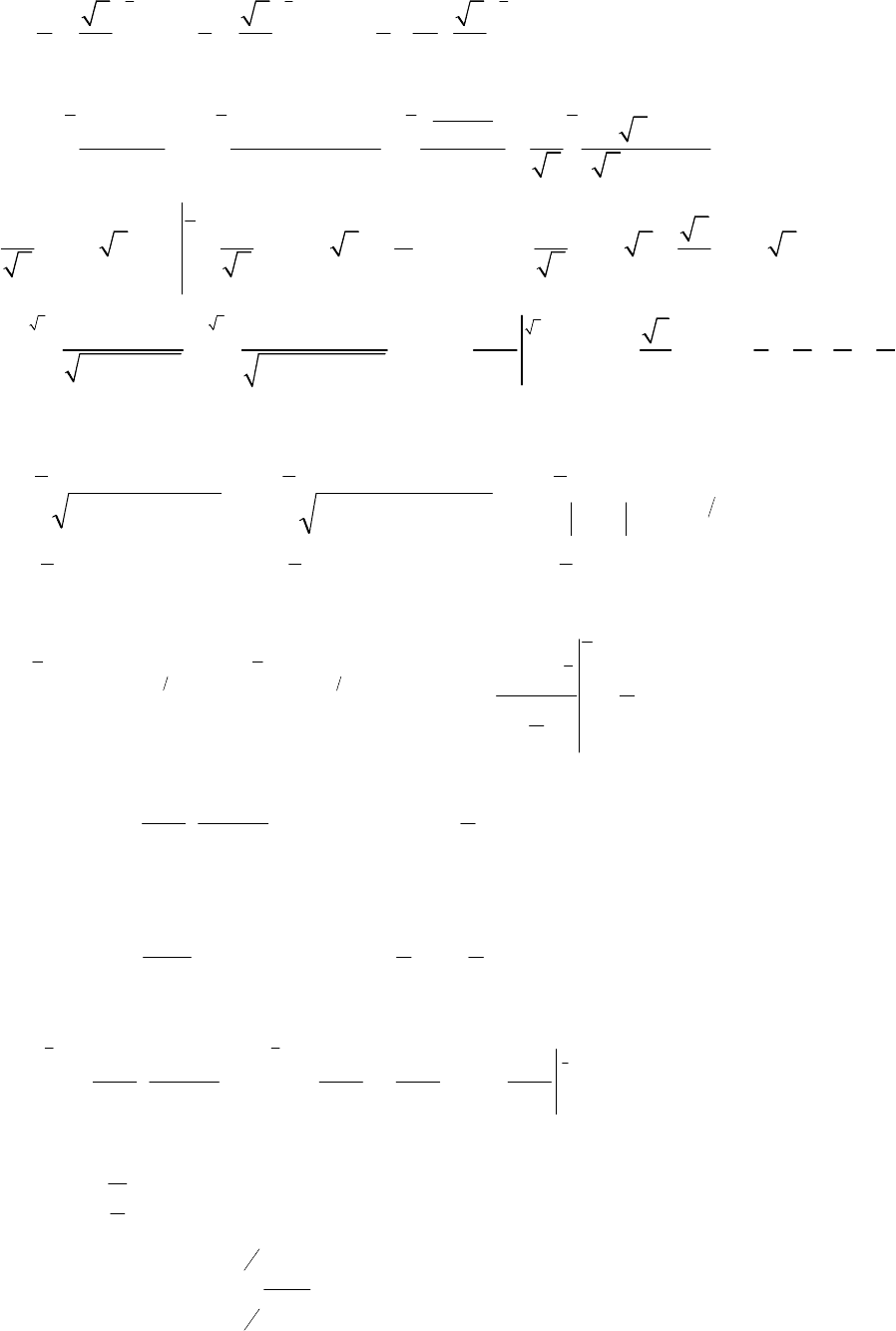
139
2 8 2
3 3 3
3 2 3 2 9 21 2
1 1
2 2 8 2 8 16 2
− − − = − +
.
3.
4 4 4 4
2
2 2 2 2
2
0 0 0 9
1 1 ( 2 )
cos
1 sin 2sin cos 2 1
2 ( 2 ) 1
dx
dx d tgx
x
I dx
x x x tg x
tgx
π π π π
⋅
= = = =
+ + +
⋅ +
∫ ∫ ∫ ∫
=
4
0
1 1 1 2
( 2 ) ( 2 0 2 2
4 2
2 2 2
arctg tgx arctg tg arctg arctg arctg
π
π
⋅ = ⋅ − = =
.
4.
3 1 3 1
3 1
2 2 2
0
0 0
( 1) 1 3 1
arcsin arcsin arcsin
2 2 2 3 6 6
3 2 ( 1) 2
dx d x x
x x x
π π π
− −
−
+ +
= = = − = − =
− − − + +
∫ ∫
.
5.
( )
( )
==−=−
∫∫∫
π
π
−
π
π
−
π
π
−
2
2
21
2
2
2
2
2
3
1 dxxcosxsindxxcosxcosdxxcosxcos
Скористаємося парністю підінтегральної функції.
( )
2
1 2
0
2 sin cos
x x dx
π
= =
∫
-
( )
2
1 2
0
2 cos (cos )
x d x
π
=
∫
( )
2
3
2
0
cos
4
2
3
3
2
x
π
− ⋅ =
.
6.
Обчислити середнє значення функції
2
1
( ) cos
1 (1 )
f x
x x
π
= ⋅
− −
на відрізку
1
0;
2
.
Розв’язання. Середнє значення функції за теоремою про середнє
дорівнює:
1 1 1
( ) ( ) , ãäå 0
2 2
b
a
f f x dx b a
b a
ξ
= − = − =
−
∫
.
1
2
0
1 1
2 2
2
0 0
1 1
cos cos sin sin 2 sin 0
1 (1 ) 1 1 1
dx d
x x x x x
π π π
π π
⋅ = = = − =
− − − − −
∫ ∫
.
Отже, середнє значення функції дорівнює
1
( ) 0 0
1
2
f
ξ
= ⋅ =
.
7.
Оцінити інтеграл
2
4
sin
x
dx
x
π
π
∫
.
Точне значення інтеграла в цьому випадку знайти не можна, тому що
первісна не виражається через елементарні функції.
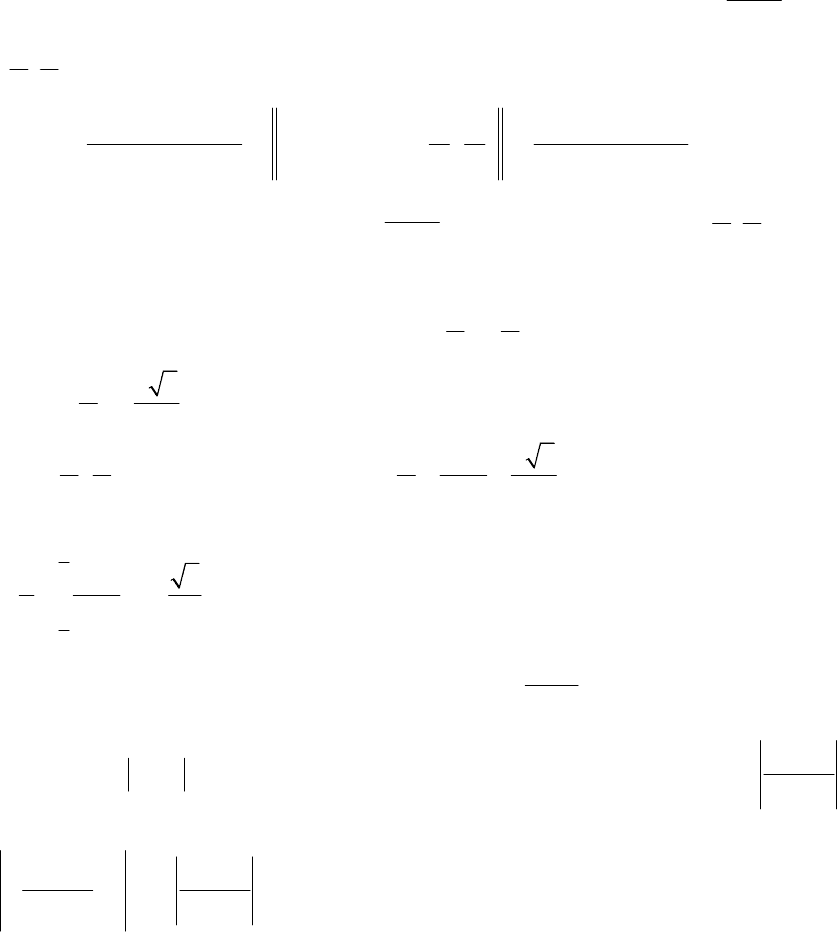
140
Для дослідження поведінки підінтегральної функції
( )
x
xsin
xf =
на відрізку
;
4 2
π π
знаходимо її похідну:
( )
(
)
0
x
xcostgxx
3
;
4
x,tgxx
x
xsinxcosx
xf
22
<
−
=
∈<=
−
=
′
ππ
Підінтегральна функція
( )
x
xsin
xf =
спадає на відрізку
;
4 2
π π
, тому що її
похідна
(
)
0.
f x
′
<
.
Найменше значення функції
2
2
m f
π
π
= =
, а найбільше значення функції
2 2
4
M f
π
π
= =
.
;
4 2
x
π π
∀ ∈
має місце нерівність:
2 sin 2 2
x
x
π π
≤ ≤
.
Скориставшись теоремою про оцінку інтеграла, одержимо:
2
4
1 sin 2
2 2
x
dx
x
π
π
≤ ≤
∫
.
8. Оцінити абсолютну величину інтеграла
19
8
10
sin
1
x
dx
x+
∫
.
Оскільки 1xsin
≤
, то при
10
x
>
виконується нерівність
8
8
10
x1
xsin
−
≤
+
.
Використовуючи властивість 7, одержимо :
( )
78
19
10
8
19
10
8
10101019dx
x1
xsin
dx
x1
xsin
−−
<−<
+
<
+
∫∫
.
Заміна змінної в визначеному інтегралі
Нехай функція
(
)
f x
неперервна на
[
]
,
a b
, а функція х=
(
)
t
ϕ
– монотонна
й має неперервну похідну на відрізку
[
]
,
α β
, де
(
)
a
ϕ α
=
,
(
)
b
ϕ β
=
, тоді має
місце формула заміни змінної в визначеному інтегралі
( ) ( )( ) ( )
∫∫
′
=
β
α
ϕϕ
dtttfdxxf
b
a
.
Зауваження. Заміну змінної інтегрування звичайно роблять за
допомогою монотонних неперервних функцій, тому що монотонність
гарантує однозначність як прямої, так і оберненої функції. При цьому, якщо
змінна t змінюється в проміжку
[α
;
β]
, значення функції
(
)
t
ϕ
не повинні
виходити за межі проміжку [a, b].
