Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1

Подождите немного. Документ загружается.

291

Некоторое снижение потерь в стали при увеличении не-

сущей частоты ШИР ПЧ, показанное в табл.6.2, связано с

уменьшением тока от гармоник выходного напряжения,

имеющих частоты близкие к

нес

Низкочастотные составляющие напряжения на выходе

ПЧ задаются суммарным углом проводимости транзисторов



и остаются практически неизменными при указанном

способе регулирования напряжения ПЧ.

Вихревые токи в стали статора и ротора оказывают влия-

ние на величину электромагнитного момента ВД. Завышение

величины момента, подсчитанного без учета действия вихре-

вых токов, может достигать 20%. Например, на расчетной

осциллограмме (рис.6.14) в конце одного из интервалов (при







с) модуляционного выключения транзисторов (на

таких интервалах вихревые токи особенно сильно выражены)

минимум электромагнитного момента составит 16,37 Нм

вместо 19,62 Нм при неучете действия вихревых токов.

Выводы

1. Предложена электрическая схема замещения магнито-

электрического синхронного двигателя и способ определения

ее параметров, позволяющая оценить влияние вихревых то-

ков в стали статора и ротора на величину потерь и электро-

магнитный момент двигателя при его питании от ПЧ.

2. Математическая модель ВД учитывает основные физи-

ческие особенности режима его питания и допускает вариа-

цию алгоритмов управления вентилями ПЧ.

3. Вихревые токи в стали статора и ротора оказывают

влияние на величину электромагнитного момента ВД. Завы-

шение величины момента, подсчитанного без учета действия

вихревых токов, может достигать 20%.

4. Для увеличения момента двигателя при заданном уров-

не перегрева обмотки статора, упрощения технологии его

изготовления целесообразно полюсные сердечники ротора

выполнять шихтованными.

292

6.3. Математическая модель вентильной машины

с электромагнитным возбуждением в фазных координатах

6.3.1. Общие замечания

Теория вентильных электрических машин базируется на мате-

матических моделях, характеризуемых иерархическим уровнем ис-

ходных допущений. Содержание принятых допущений диктуется

прежде всего назначением модели и временем реализации ее вы-

числительных алгоритмов. К моделям наиболее низкого уровня

следует отнести те, в которых не учитываются дискретные и нели-

нейные свойства электрической машины и преобразователя часто-

ты. Модели этого уровня и близкие к ним, требующие минималь-

ного времени для численной реализации на ЭВМ, широко исполь-

зуются в расчетах функциональных режимов электромеханических

систем с вентильными электрическими машинами (автономных

источников электроэнергии, автоматизированных электроприводов

и др.). В моделях высокого уровня обычно учитываются такие осо-

бенности, как нелинейность стальных участков магнитной цепи

машины, дискретность расположения проводников и работы вен-

тилей преобразователя частоты [277, 226], двухсторонняя зубчатость

стальных сердечников [167], эффект вытеснения тока в проводни-

ках обмоток индуктора [208] и др. Эти модели используются как

для анализа и оптимизации работы самих машин, так и в практике

их проектирования.

В настоящем разделе рассматривается математическая

модель в фазных координатах, в которой сделана попытка

достаточно корректного учета вышеназванных специфиче-

ских свойств вентильной машины (ВМ).

6.3.2. Исходные допущения, принципиальные особенности

модели

Основные допущения следующие:

1) магнитное поле (МП) ВМ плоскопараллельно;

2) МП рассеяния не зависит от главного МП;

3) расчетная область воздушного зазора (ВЗ) одномерная

— средняя окружность;

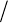
293

4) вентильные элементы представлены кусочно-линейны-

ми резисторами, шунтированными

r — C

ветвями.

Магнитное напряжение в счетной точке ВЗ определяется

зависимостью:

F B

 

 

, (6.68)

где



— радиальная составляющая магнитной индукции ВЗ;

  







; (6.69)



— минимальный ВЗ,



— дополнительные составляющие длины ВЗ, обуслов-

ленные четырьмя типовыми зубчатыми структурами: по-

люсами индуктора (



); зубцами якоря (



); зубцами на

поверхности полюсного наконечника индуктора (



); не-

равномерностью ВЗ между гладкими поверхностями яко-

ря и полюсного наконечника (



Каждая составляющая



находится раздельно при ра-

венстве нулю остальных. Методика их расчета изложена в

параграфах 1.3 и 2.2.

Нахождение



для средней окружности ВЗ, а не для

окружности гладкого сердечника, как это принято в класси-

ческом методе удельной проводимости, обеспечивает лучшее

приближение к результатам точного расчета МП при двух-

сторонней зубчатости ВЗ, особенно при относительно боль-

шом значении 

. В массиве исходных данных модели ис-

пользуются периодические зависимости вида





 ,

(

 1 3 4, , );





  , полученные путем сплайновой аппрокси-

мации на периоде их изменения. Здесь



— координаты

счетной точки ВЗ в системах координат, жестко привязан-

ных соответственно к индуктору и якорю, начальные точки

которых совпадают с осями

индуктора и фазы

якоря.

Таким образом магнитная проводимость области ВЗ (на рис.

6.15 она выделена жирными линиями) определяется по ис-

ходным данным, полученным полевым методом на предва-

рительной стадии расчета.

294

Рис. 6.15. К расчету магнитного поля явнополюсной синхрон-

ной машины

Особенности идентификации счетных точек и методика рас-

чета значений магнитной индукции в них изложены в пара-

графе 2.2.

Проводники всех

обмоток ВМ (одной независимого

(

н ) и двух последовательного возбуждения (

fd fq

c; c ), трех

фаз якоря (

A B C

; ; ) и демпферной ( ДО ) с

контурами),

электрическая схема которой изображена на рис. 6.4, пред-

полагаются углубленными в пазы [150]. При заданных на-

чальных значениях вектора с независимыми токами обмоток:





п н Д1 Д2



i i i i i i i

А B fd Дr

... , (6.70)

где

п1

— ток звена постоянного тока преобразователя часто-

ты (ПЧ), протекающий через сглаживающий дроссель и

последовательные обмотки возбуждения ВМ;

, (

k r

= 1,2,... ) — контурный ток

-го участка ДО, со-

стоящего из двух соседних стержней и перемычек между

ними,

и углового положения ротора



вычисляются (в результате

решения системы нелинейных уравнений (2.13)—(2.15)) маг-

295

нитная индукция







 и по формуле (3.41) коэффициенты

насыщения магнитной цепи







 в 2

1 1

Q n Z





счетных точ-

ках воздушного зазора с локально учитываемой зубчатостью.

С помощью формул (3.49), (3.50) находятся статические ин-

дуктивности само- и взаимоиндукции и потокосцепления обмо-

ток, обусловленные магнитным потоком воздушного зазора.

После вычисления двух типов производных (частной и

полной) от индуктивностей обмоток путем численного диф-

ференцирования выражения (3.49) — по угловой координате

ротора  

 

L L





и по времени

d dtL



— имеем возмож-

ность определить по формулам (3.51) и (3.52) электромагнит-

ный момент и ЭДС обмоток. Производная первого типа на-

ходится при постоянстве вектора тока (6.70) и фиксирован-

ном приращении угловой координаты



, производная вто-

рого типа — путем вычисления приращений индуктивностей

обмоток (3.44) на каждом шаге интегрирования дифференци-

альных уравнений ВМ.

По обмоткам ВМ протекают принципиально несинусои-

дальные токи, которые вызывают помимо основных также и

добавочные потери, обусловленные вихревыми токами как в

самих проводниках, так и в прилегающих к ним частях маг-

нитопровода. Для учета частотных свойств проводников об-

моток в собственном поле рассеяния целесообразно послед-

ние представить как пассивные двухполюсники, схемные

функции которых удовлетворяют заданным частотным харак-

теристикам, найденным из опыта или расчета. Схемные

функции таких двухполюсников, относящиеся к классу по-

ложительных вещественных функций [269], могут быть реа-

лизованы методами синтеза электрических цепей, на основе

которого определяются топология, набор и значения частот-

но-независимых параметров

r, L, C

. Применительно к об-

моткам электрических машин, обладающих активным сопро-

тивлением и индуктивностью рассеяния, можно задаться то-

пологией синтезируемой цепи, выбрав ее в виде параллель-

но-включенных ветвей, состоящих из резистора

и индук-

тивности

(

j n

 1 2, ,... ), значения которых подлежат рас-

296

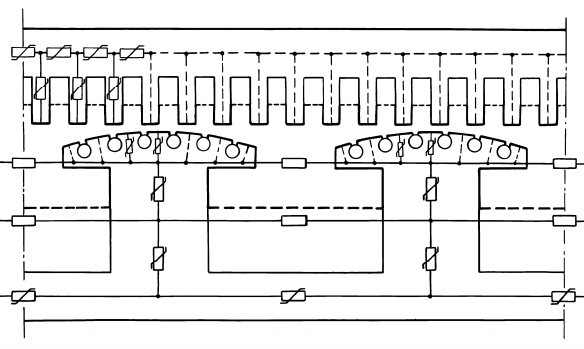
чету. Наиболее значительно эффект вытеснения тока прояв-

ляется в проводниках обмоток индуктора. Фрагмент (контур

с номером

) схемы ДО, каждый стержень и коротко-

замыкающие перемычки которого представлены набором

частотно-независимых параметров, изображен на рис. 6.16, а.

Рис. 6.16. К расчету токов обмоток ротора

297

Дифференциальное уравнение равновесия напряжения для

этого контура имеет вид:

   

d dt L di dt L di dt

k k





  

 

1 1

   

    

 

L d i dt r i r i r i

k k k k

k k

п с

с с

п п

1 1 1

, (

k r

= 1,2,... ).

(6.71)

Для нахождения токов ветвей

-й перемычки (

i n

1 2, ,...

) к уравнению (6.71) следует добавить (

1) диф-

ференциальных уравнений, соответствующих электрическому

равновесию (

 1 ) независимых контуров из ветвей ука-

занной перемычки

L i r i

п п п п

k k k k

  , (6.72)

где

п п

k k

L L



















1 2

2 3

0 0 0

...

... ... ... ... ... ...

...

, (6.73)

п п

k k

r r



















1 2

2 3

0 0 0

...

... ... ... ... ... ...

...

— (6.74)

прямоугольные матрицы размером (

 1 )



;

и n

- числа параллельно включенных ветвей в схемах

замещения соответственно стержня и перемычки. На рис.

6.16, а имеем: n n n

c п

 

298





п п

k k

i i i



1 2

...

. (6.75)

Равновесие напряжений (

 1 ) независимых контуров

из

ветвей

-го стержня описывается дифференциальными

уравнениями:

L i r i

c c c

k k k

  , (6.76)





L di dt L di dt r i r i

с с с с с с с с

   

   

1 1 1 1

, (6.77)

где

c c

k k

L L

















 

1 2

2 3

2 1

0 0 0

...

... ... ... ... ... ...

...

, (6.78)

c c

k k

r r

















 

1 2

2 3

2 1

0 0 0

...

... ... ... ... ... ...

...

— (6.79)

прямоугольные матрицы размером (

 2 )



(

 1 ),





c c c c

k k k k

i i i





1 2

... . (6.80)

Для токов стержней и перемычек имеем:

i i

k k

c c





;

i i

k k

п п





. (6.81)

Принимая во внимание данные рис. 6.16, а,

299

i i i

k k k

п c п( -1)

  ;

i i

k k

п Д

 , (6.82)

получим с учетом первого равенства (6.81):

 

i i i i

с п

  









. (6.83)

Дифференциальное уравнение (6.77) с использованием

формулы (6.83) преобразуется к виду:

   

L i L i L i r i r i r i

с с с

с п с с с

с п

k k

d dt d dt d dt

     

 1 1

(6.84)

где









с с с с

с с с

L L L

 



1 1 1 1

... , (6.85)









с с с

r r r





11 1 1

... — (6.86)

векторы-строки с размером (

 1 );





с с

 1 1 1... , (6.87)





с с

 1 1 1... — (6.88)

векторы-строки с размером

Дифференциальные уравнения (6.71), (6.72), (6.76), (6.84)

определяют (

n n

п c

  1 ) независимых токов ветвей

-го кон-

тура ДО.

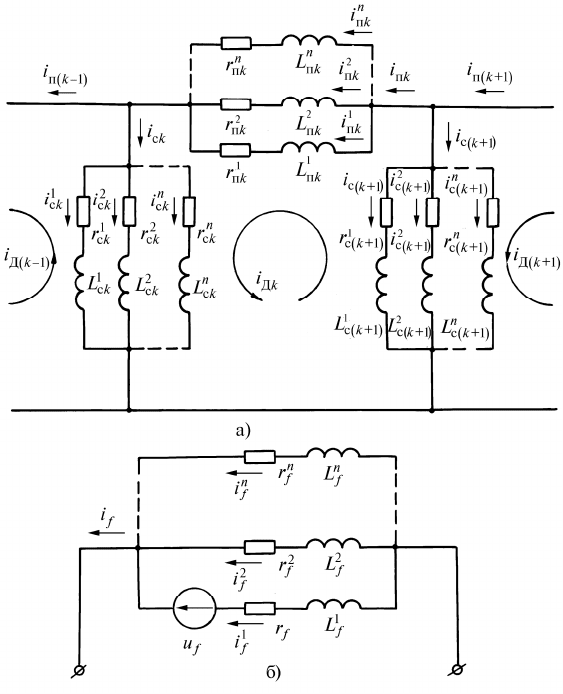
Применительно к обмотке возбуждения (рис. 6.16, б) бу-

дем иметь

Сопротивление

выбирается равным сопротивлению обмотки

возбуждения на постоянном токе

300

d dt L di dt r i u

f f f f f





   

1 1 1 1

;

i i

f f





, (6.89)

причем для вектора тока





f f f

i i i



1 2

...

справедливо диф-

ференциальное уравнение

L i r i u

f f f f f

   , (6.90)

где матрицы

совпадают с матрицами (6.73), (6.74),

если в последних принять п 

n n

 и опустить ин-

декс

;





f f

 0 0 0...

Система дифференциальных уравнений трехфазной ВМ,

имеющая размерность

h n n n r

    20 1( )

п c

, может быть

разрешена относительно производных переменных состоя-

ния и представлена в нормальной форме Коши:

A x fd dt

 , (6.91)

где





x i i i i u



i i i

А B f

п п с

  ;





~ ~



i i

a b

— вектор токов двух фаз питающей сети;

i i

п с

, — векторы токов перемычек и стержней демпфер-

ной обмотки с размерами соответственно

n r





n r

 1 ;





c c c c

u u u



1 2 13

...

— вектор напряжений емкостей защит-

ных цепочек вентилей преобразователя частоты (двух

его мостов и дополнительного тиристора в звене по-

стоянного тока);