Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1
Подождите немного. Документ загружается.

111
Âыводы
1. Предложена методика расчета магнитного поля
СДПМ, позволяющая учесть основные физические факторы:
зубчатость BЗ, дискретность распределения проводников и
насыщение магнитной цепи.
2. Решение исходных нелинейных уравнений предлагае-
мого метода может быть реализовано численным способом
на основе метода продолжения решения по параметру.
3. Изготовленные и рассчитанные по этой методике об-
разцы СДПМ с роторами «коллекторного» типа показывают,
что при оптимальном проектировании такие двигатели даже
на оксидно-бариевых магнитах не менее чем в 1,5 раза пре-
восходят АД по развиваемому моменту в одном и том же га-
барите, т.е. могут быть выполнены на габарит меньше, чем
АД при одном и том же моменте на валу, и перспективны
для применения в современном станочном электроприводе.
2.4. Магнитоэлектрические машины с аксиальным прин-
ципом концентрации магнитного потока
В электроприводах механизмов подачи металлорежущих
станков на диапазон моментов 0,35...35 Нм получают рас-
пространение высокомоментные вентильные двигатели с по-
стоянными магнитами (ферритовыми, самарий-
кобальтовыми и др.), преобразователь которых представляет
транзисторный инвертор напряжения, регулируемый широт-
но-импульсным способом [214, 235]. При больших значениях
моментов (47Нм и выше) на передний план выступают во-
просы рекуперации энергии при торможении двигателя, ко-
торые в транзисторных электроприводах решаются сравни-
тельно сложно. В этом случае целесообразно использовать
тиристорный непосредственный преобразователь частоты
(НПЧ) с двухфазным выходом, обеспечивающий двухсто-
ронний обмен энергией с сетью. В таком варианте электро-
привод на основе двухфазного синхронного двигателя даже с
ферритовыми магнитами (СДПМ) имеет лучшие технико-
экономические показатели, чем аналогичные системы элек-
тропривода с асинхронными двигателями и высокомомент-
ными двигателями постоянного тока.
112
Номинальные значения скорости вращения двигателя
(1500 об/мин) и выходной частоты НПЧ (50 Гц) определяют
четырехполюсное исполнение СДПМ. В этой ситуации при-
менение ферритовых магнитов, имеющих низкий уровень
остаточной индукции, исключает использование конструк-
ции индуктора «коллекторного» типа (с тангенциальным на-
магничиванием магнитов), которая обеспечивала бы необхо-
димую концентрацию магнитного потока в воздушном зазоре
двигателя только при достаточно большом числе полюсов (не
ниже шести).
Эффект концентрации магнитного потока может дости-
гаться также и при малополюсном индукторе путем увеличе-
ния полезной площади магнитов за счет их зигзагообразного
расположения на полюсах [22, 296]. Однако опытное макети-
рование СДПМ на высоте оси вращения 132 мм показало,
что четырехполюсный индуктор такого типа обладает срав-
нительно низкой устойчивостью к размагничиванию (малой
кратностью тока перегрузки, равной 2...3. Еще более низкий
ток перегрузки был зафиксирован на макете СДПМ с высо-
той оси вращения 160 мм. Тенденция к снижению перегру-
зочной способности двигателя с увеличением его высоты оси
вращения объясняется относительно замедленным ростом
рабочей толщины магнитов по сравнению с ростом МДС
обмотки якоря, пропорциональной произведению A/2.
Наиболее целесообразным способом увеличения индук-
ции магнитного поля в рабочем зазоре СДПМ с сердечником
статора заданной длины является применение аксиального
принципа концентрации магнитного потока, при котором
длина ротора выбирается в 1,5...2 раза больше длины сердеч-
ника статора.
2.4.1. Особенности конструкции СДПМ с аксиальным спосо-
бом концентрации магнитного потока
Двухфазный четырехполюсный синхронный двигатель с
постоянными феррито-стронциевыми магнитами на момент
47 Нм (в стопорном режиме, без наружного обдува) был
спроектирован и изготовлен на базе статорного сердечника,
станины и щитов асинхронной машины типа 4А132М6, раз-
вивающей в аналогичном режиме момент 41 Нм. Выбор шес-
113
типолюсной базовой машины продиктован ожидаемым по-
нижением магнитной индукции в воздушном зазоре СДПМ
из-за низкой остаточной индукции магнитов (0,35 Тл) и, как
следствие, уменьшением индукции в ярме статора. Шести-
полюсная машина по сравнению с четырехполюсной имеет
при заданном внешнем диаметре сердечника статора, опре-
деляемом высотой оси вращения ротора, меньшее сечение
ярма и больший диаметр расточки статора. Последнее об-
стоятельство позволяет повысить значение электромагнитно-
го момента СДПМ при прочих равных условиях.
Осевая длина ротора увеличена в 1,78 раза по сравнению
с длиной сердечника статора. Для проведения магнитного
потока по лобовым участкам полюсов в осевом направлении
необходимы полюсные наконечники с соответствующим по-
перечным сечением массивного типа или со специальной
аксиально-радиальной шихтовкой. Для макетного образца
были выбраны массивные наконечники с равномерным воз-
душным зазором 0,5 мм. Ярмо ротора может быть массив-
ным или набранным из листов стали с обычной радиальной
шихтовкой. В опытном образце ярмо массивное, изготовлен-
ное заодно с валом из стали 45.
Магниты закреплены с помощью клея и полюсных нако-
нечников, привинченных к четырехгранному ярму немаг-
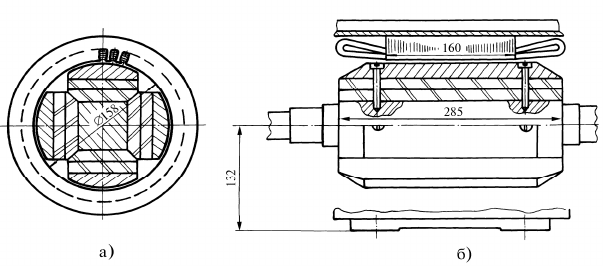
нитными болтами (рис. 2.9).
Рис. 2.9. Конструктивная схема двигателя: поперечный (а), и про-
дольный (б) разрезы
114
Для уменьшения потерь от вихревых токов наружная по-
верхность полюсных наконечников подвергнута рифлению
кольцевыми канавками [218] глубиной 1,5 мм, шириной 0,5
мм и с шагом 2,5 мм. Это мероприятие позволило увеличить
электромагнитный момент стопорного режима с номиналь-
ной токовой нагрузкой на 7,5 %. Тепловые испытания пока-
зали, что на квалификационных частотах вращения 10 и 375
об/мин двигатель развивает электромагнитный момент соот-
ветственно в 51 и 47 Нм.
Предложенный аксиальный способ концентрации маг-
нитного потока позволил поднять уровень индукции в воз-
душном зазоре СДПМ до значения 0,58 Тл, составляющего
79% от ее величины у базовой асинхронной машины. При
этом удалось сохранить массу ротора синхронной машины
такой же как и у базового двигателя, во-первых, за счет бо-
лее низкой удельной массы материала магнитов по сравне-
нию с электротехнической сталью, во-вторых, благодаря дос-
таточно большим межполюсным окнам на роторе.
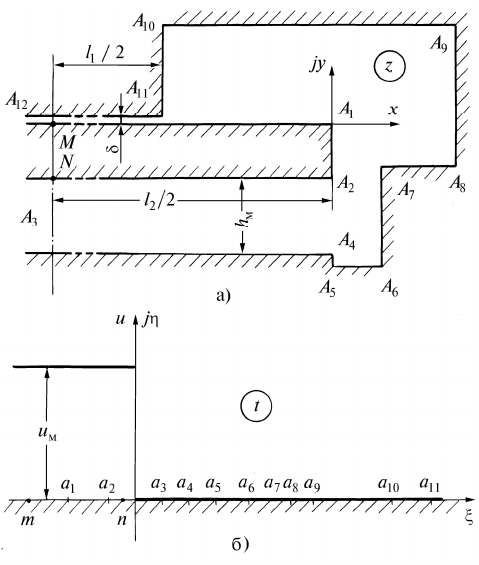
Сравнительные данные отечественных и зарубежных
электродвигателей с ферритовыми магнитами для привода
подачи станков с номинальными моментами выше 35 Нм
приведены в табл. 2.2. Опытные образцы рассматриваемых
двигателей получили наименование 4СХ2П132М4. Их пока-
затели фигурируют в первой строке (сверху) табл. 2.2.
Таблица 2.2
Тип Показатели
двигателя М
н
,
Нм
n
max
,
об/мин
G
,
кг
d
фланца
,
мм
J
,
кг
.
м
2
М
н
/
G,
Нм/к
г
Т
эм
,
с.
4СХ2П132М4 51 1500 100 265 0,09 0,51 0,055
SD—A6.480.020,
Bosch
, ФРГ
48 2000 115 260 0,135 0,42 0,098
FRP23—038-20,
Stromag, ФРГ
38 2000 79 215 0,0376 0,48 0,035
2ПБВ132МУ3 47,8 2000 130 265 0,188 0,37 0,092
4А132М4
(деноминализи-
рованный)
35 1500 82 300 0,04 0,43 0,030
115
2.4.2. Расчет магнитного поля СДПМ
Постоянные магниты полюсов ротора, длина которого
существенно превышает длину сердечника статора, создают
магнитное поле (МП) рассеяния со сложным пространствен-
ным распределением в зоне, ограниченной лобовыми участ-
ками полюсного наконечника, торцом пакета статора, щитом
и станиной корпуса. Это поле, перемещаясь вместе с рото-
ром, будет наводить вихревые токи и, следовательно, являть-
ся источником потерь в неподвижных ферромагнитных уча-
стках границы указанной зоны. Очевидно тепловыделение в
подшипниковом щите, зависящее от его близости к возбуж-
денному торцу ротора, должно быть учтено при выборе ве-
личины удлинения ротора.
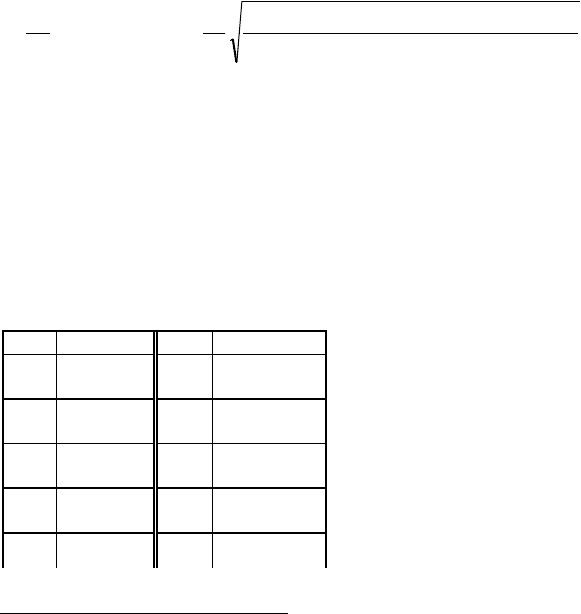
Рис. 2.10. К расчету магнитного поля двигателя
116
Произведем расчет МП в осевой продольной плоскости, ис-
пользуя метод конформных отображений. Внутренность две-
надцатиугольной незамкнутой области
А
1
А
2
...А
12
комплекс-
ной плоскости
z
(рис. 2.10, а) продольного разреза СДПМ,
прямоугольная полоса
А
2
А
3
А
4
которой представляет сечение
постоянных магнитов, может быть отображена на верхнюю
комплексную полуплоскость
t
(рис.2.10,б). Соответствие то-
чек этих областей задается дифференциальным уравнением
Кристоффеля-Шварца:
dz
dt
t
,
t
t
t a t a t a t a t a
t a t a t a t a t a
1 2 4 7 11
5
6
8 9 10
.
(2.49)
Три из двенадцати постоянных отображения
a
j
(
j
1 2 12, ,..., ) могут выбираться произвольно. Примем:
a
1
10 ;
a
3
0 ;
a
12
. Остальные находятся в результате
решения численными методами системы интегральных урав-
нений, выражающих соответствие длин отрезков границ об-
ластей в плоскостях
z
и
t
[52]. Найденные значения посто-
янных для исследуемого двигателя с
10
3
м приведены в
табл. 2.3
2
.
Реальным точкам
M
и
N
(рис. 2.10, а), в ко-
торых верхние и нижние
поверхности полюсного
наконечника пересека-
ются поперечной плос-
костью, проходящей че-
рез геометрический
центр ротора, отвечают
их образы на плоскости
t
с координатами
m
и
n
по оси (рис. 2.10, б).
2
Точность расчета определенных интегралов - 10
—7
; максимальная
невязка при выходе из итераций - 10
—6
.
Таблица 2.3
j a
j
j a
j
2
-0,15702
8 3,70304
4
0,03206 9 9,09035
5
0,03665 10 2852,26
6
0,04332 11 3284368
7
0,72298 -
-

117
Эти координаты, зависящие от длины ротора
l
2
, могут быть
найдены с помощью следующих интегральных уравнений:
t dt l
m
a
1
2
2
;
t dt l
a
n
2
2
2
. (2.50)
В результате вычислений по формулам (2.50) получено:
m
10
11116,
;
n
0 5446 10
8
, .
Пренебрегая насыщением магнитной цепи, примем маг-
нитный потенциал полюсных наконечников равным
U
м
, а
остальных участков границы области
А
1
А
2
...
А
12
— равным
нулю. На рис. 2.10, б показан график изменения магнитного
потенциала границы области в плоскости
t
.
Область
t
можно подвергнуть дополнительному кон-
формному преобразованию вида
z
h
t
1
м
ln , (2.51)
которое обращает верхнюю полуплоскость
t
в горизонталь-
ную бесконечную полосу высотой
h
м
(
h
м
—
высота постоян-
ных магнитов (см. рис.2.10,а)), фиксированную в комплекс-
ной плоскости
z x jy
1 1 1
. Преобразование (2.51) переводит
точку
t a
3
0 в левый край указанной полосы, находящей-
ся в бесконечности. Комплексная потенциальная функция
W V jU
U
h
z
U
t
м
м
м
1
ln , (2.52)
сообщая верхней границе рассматриваемой полосы скаляр-
ный магнитный потенциал
U
м
,
описывает равномерное маг-
нитное поле в этой полосе с напряженностью

118
H
z
j
dW
dz
j
U
h
1
1
м
м
(2.53)
и функциями потока
V x U h
1 м м
и скалярного потенциала
U y U h
1 м м
.
Используя выражения (2.49), (2.52), можно рассчитать
комплексно сопряженный вектор напряженности магнитного
поля в исходной плоскости
z
:
H
j
dW
dz
j
dW
dt
dt
dz
j
U
t t
м
1
. (2.54)
Формула (2.54) позволяет получить
H H R
x m H H
1
sin ;
H H R
y m H H
1
cos , (2.55)
где
R e
t a t a t a t a t a
t a t a t a t a t a
H
j
H
5
6
8 9 10
1 2 4 7 11
; (2.56)
H U
m
1
м
.
Левой части бесконечной полосы
А
2
А
3
А
4
плоскости
z
(см.
рис. 2.10,а), занятой магнитным сплавом, соответствует уча-
сток верхней плоскости
t
(см. рис. 2.10,б), примыкающей к
началу координат, для которого
t
0
. При подстановке в
формулу (2.56)
t
=0 получим:
R h
H
м
;
H
. В результа-
те для этой части указанной полосы справедливо:
H
x
0 ;
H H U h
y m
2 м м
.
При известной напряженности магнитного поля в зоне,
занятой постоянным магнитом, составляющие его вектора
намагниченности находятся из уравнений:

119
M M k H k H
M M k H k H
x rx xx x xy y
y ry yx x yy y
. (2.57)
При практическом использовании уравнений (2.57) целе-
сообразно элементы тензора магнитной восприимчивости и
составляющие остаточной намагниченности принять равны-
ми[169]:
k k
yy
;
k k
xx
;
k k
xy yx
0 ;
M
rx
0 ;
M M
ry r
,
где , — индексы осей соответственно параллельных и
перпендикулярных направлению магнитной текстуры.
Для составляющих вектора магнитной индукции в зоне
расположения магнитов справедливо:
B H M
x x x
0
;
B H M
y y y
0
. (2.58)
В соответствии с формулой (2.52) в плоскости
t
для точки
t R j
exp ) функция потока вектора
H
V U R
H
м
ln . (2.59)
Используя эту формулу и принцип инвариантности функции
потока при конформных преобразованиях [155], получим
выражение для потока вектора
Н
через поверхность полюс-
ного наконечника (на участке
MA
1
A
2
N
; см. рис. 2.10,а):
V V V U m n
H H
m
H
n
м
ln . (2.60)
На нижней поверхности полюсного наконечника (участок
A
2
N
на рис. 2.10,а), в соответствии с зависимостями (2.57),
вектор намагниченности
M
jM j M k H
y r y
. (2.61)

120
Поток этого вектора через указанную нижнюю поверхность
полюсного наконечника
V Mdx
M
l
0
2
2
с учетом формулы (2.59) будет определяться выражением
V M l k U a n
M r
2 2
2
м
ln . (2.62)
Принимая во внимание, что поток вектора магнитной ин-
дукции через замкнутую поверхность полюсного наконечни-
ка (линия
MA
1
A
2
NM
на рис. 2.10, а) всегда равен нулю, мо-
жем утверждать в соответствии с формулой (2.58):
V V
H
M
0 . (2.63)
Последнее равенство позволяет определить магнитный по-
тенциал полюсного наконечника (
U
м
) при известной оста-
точной намагниченности материала магнита (
M
r
) (величи-
на
M
r
является справочной [238]):
U l M m n a n
r
k
M
2 2
2 ln . (2.64)
Зная
U
м
, можем рассчитать максимальное
B
m
1
и среднее
B
m
значение магнитной индукции в воздушном зазоре
СДПМ:
B U
m
1 0
м
;
B U k
m
0 м
,
где
k k k
1 2
— коэффициент воздушного зазора, учиты-
вающий зубчатость статора и ротора.
При применении ферритостронциевых магнитов типа
24СА200, имеющих данные [238]:
M
r
0 37
0
. A/м;
k
0148, , получим для опытного двигателя (
l
2
0 285 , м),
используя формулу (2.64):
U A
м
474 94, ;
B
m
1
0 597 , Тл.
