Appel W. Mathematics for Physics and Physicists
Подождите немного. Документ загружается.

Tables
609
Fourier Transfor ms
The convention used here is the following:
e
f (ν)
def
=
Z
+∞
−∞
f (x) e
−2iπν x
dx and f (x) =
Z
+∞
−∞
e
f (ν) e
2iπν x
dν.
For other standard conventions, see the table on page 612.
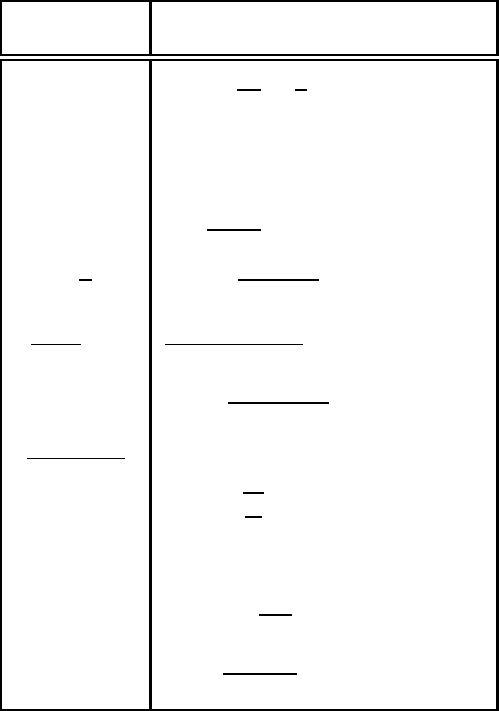
f (x)
e
f (ν)
f (ax)
1
|a|
e
f
ν
a
f
(n)
(x) (2iπν)
n
e
f (ν)
(−2iπx)
n
f (x)
e
f
(n)
(ν)
Π(x)
sin πν
πν
= sinc πν
Π
x
a
sin πν |a|
πν
1
b − a
χ
[a,b]
sin
π(b −a)ν
πν
e
−iπ(a+b)ν
(b > a)
e
−µ|x|
2µ
µ
2
+ 4π
2
ν
2
(µ > 0)
2a
a
2
+ 4π
2
ν
2
e
−a|ν|
(a > 0)
e
−σ x
2
r
π
σ
e
−π
2
ν
2
/σ
(σ > 0)
1 δ
x −
1
2iπ
δ
′
x
k
1
(−2iπ)
k
δ
(k)

610 Tables
f (x)
e
f (ν)
H (x)
δ
2
+
1
2iπ
pv
1
ν
H (−x)
δ
2
−
1
2iπ
pv
1
ν
sgn(x)
1
iπ
pv
1
ν
pv
1
x
−iπ sgn ν
sin(2πν
0
x)
1
2i
δ(ν −ν
0
) −δ(ν + ν
0
)
cos(2πν
0
x)
1
2
δ(ν −ν
0
) + δ(ν + ν
0
)
δ(x) 1
δ(x − x
0
) e
−2iπν x
0
X(x) X(ν)
X(ax)
1
|a|
X(ν/a)

Fourier Transforms 611
Three-dimensional Fourier transforms
For the following three-dimensional Fourier transforms, the convention
chosen is
F ( k) =
ZZZ
f ( x) e
−i k·r
d
3
r, f ( r) =
1
(2π)
3
ZZZ
F ( k) e
i k·r
d
3
k.
Moreover, we put r = krk, n = r/r and k = kkk.
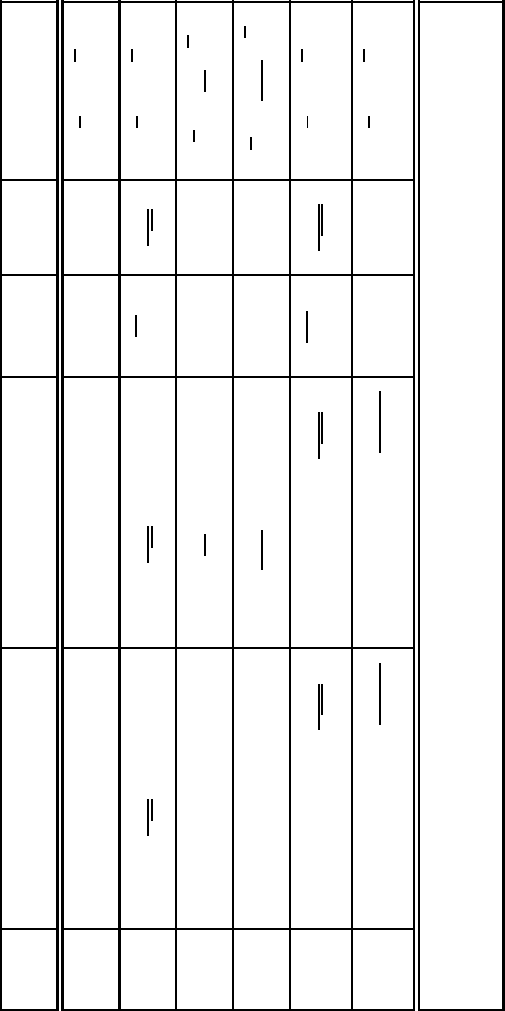
f ( r) F ( k)
△f ( r) −k
2
F ( k)
1/r 4π/k
2
e
−µr
/r 4π/(µ
2
+ k
2
) (µ > 0)
1
r
2
+ a
2
e
−ak
/2π
2
k (a > 0)
1/r
2
1/2π
2
k
1
r
( p · n)( q · n)
4π
k
2
p · q −2
( p · k)( q · k)
k
2
p, q ∈ R
3
e
−αr
2
π
α
3/2
e
−k
2
/4α
(α > 0)
δ( r) 1
1 (2π)
3
δ
612 Tables
Table of the usual conventions for the Fourier transform
Fourier transform Inverse transform F [1] F [δ] Parseval-Plancherel
e
f (ν) =
Z
f (x) e
−2iπν x
dx f (x) =
Z
e
f (ν) e
2iπν x
dν δ 1
Z
f g =
Z
e
f eg
e
f (ω) =
1
p
2π
Z
f (x) e
−iω x
dx f (x) =
1
p
2π
Z
e
f (ω) e
iω x
dω
p
2π δ
1
p
2π
Z
f g =
Z
e
f eg
e
f (ω) =
Z
f (x) e
−iω x
dx f (x) =
1
2π
Z
e
f (ω) e
iω x
dω 2πδ 1
Z
f g =
1
2π
Z
e
f eg
3D F ( k) =
ZZZ
f ( r ) e
−i k·r
d
3
r f ( r) =
1
(2π)
3
ZZZ
F ( k) e
i k·r
d
3
k (2π)
3
δ 1
Z
f g =
1
(2π)
3
Z
e
f eg
QM
(1D)
e
f (p) =
Z
f (x) e
−i p x/ }h
dx
p
2π }h
f (x) =
Z
e
f (p) e
i p x/ }h
dp
p
2π }h
p
2π }h δ
1
p
2π }h
Z
f g =
Z
e
f eg
QM
(3D)
e
f ( p) =
ZZZ
f ( x) e
−i p·x/ }h
d
3
x
(2π }h)
3/2
f ( x) =
ZZZ
e
f ( p) e
i p·x/ }h
d
3
p
(2π }h)
3/2
(2π }h)
3/2
δ (2π }h)
−3/2
Z
f g =
Z
e
f eg
Various definitions used for the Fourier transforms. The formulas for those dif ferent from the ones used in this book can be recovered by e lementary changes
of variables. The convention named “QM” are used in quantum mechanics. Note that the simplest definition in terms of memorizing the formulas is the
first one. The definition for quantum mechanics is the one in the book by Cohen-Tannoudji et al. [20]
Laplace transforms 613
Laplace transforms
In some problems (in particular, to solve differential equations while taking initial condi-
tions at t = 0 into account), it is usef u l to go through the Laplace transform, which transforms
the differential operations into algebraic operations, which can easily be inverted. The table
of Laplace transforms is therefore usually read from right to left: one looks for an “original”
t 7→ f (t) for the function p 7→ F (p) that has been calculated.
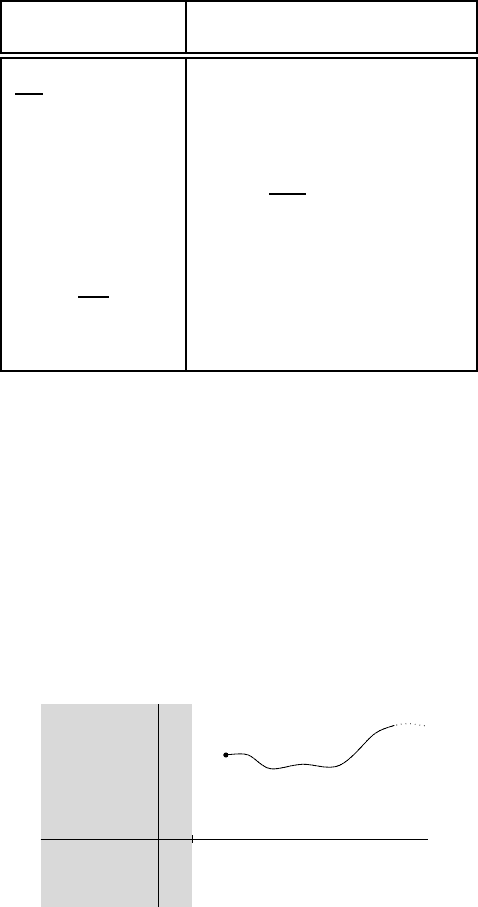
f (t) F (p) =
Z
+∞
0
e
−pt
f (t) dt
1
2iπ
Z
c+i∞
c−i∞
e
tz
F (z) dz F(p) inversion
f
′
(t) p F ( p) − f (0
+
)
Z
t
0
f (s) ds
F (p)
p
(−1)
n
t
n
f (t) F
(n)
(p) (n ∈ N)
f (t)
t
Z
∞
p
F (z) dz (∗)
e
at
f (t) F (p −a) (a ∈ C)
(∗) The i ntegral “
R
∞
p
” is defined on any path joining p to infinity “on th e right-hand side”
(Re(z) → +∞), which is entirely contained in t h e half-plane of integrability where F is
defined. B ecause F is analytic, this integral is independent of t h e chosen path.
z
α
→ ∞
614 Tables
f (t) F (p)
δ(t) 1
δ
(n)
(t) p
n
(n ∈ N)
X(t)
1
1 −e
−p
1 1/p
t 1/p
2
1/
p
πt 1/
p
p
e
at
1/(p −a) (a ∈ C)
t
n
e
at
/n ! (p −a)
−(n+1)
(n ∈ N, a ∈ C)
cos ωt
p
p
2
+ ω
2
(ω ∈ R or C)
sin ωt
ω
p
2
+ ω
2
cosh ωt
p
p
2
−ω
2
sinh ωt
ω
p
2
−ω
2
1
ω
2
(1 −cos ωt)
1
p(p
2
+ ω
2
)
(ω ∈ C)
1
ω
3
(ωt −sin ωt)
1
p
2
(p
2
+ ω
2
)
1
2ω
3
(sin ωt −ωt cos ωt)
1
(p
2
+ ω
2
)
2
t
2ω
cos ωt
p
(p
2
+ ω
2
)
2
1
2ω
(sin ωt + ωt cos ωt)
p
2
(p
2
+ ω
2
)
2

Laplace transforms 615
f (t) F (p)
t cos ωt
p
2
−ω
2
(p
2
+ ω
2
)
2
J
0
(ωt)
1
p
p
2
+ ω
2
ω J
1
(ωt) 1 −
ω
p
p
2
+ ω
2
ω
J
1
(ωt)
t
p
p
2
+ ω
2
− p
log t −
log p
p
−γ (γ ≈ 0 , 577...)
p
π
Γ(k)
t
2ω
k−
1
2
J
k−
1
2
(ωt)
1
(p
2
+ a
2
)
k
(k > 0)
616 Tables
Tables of probability laws
Discrete laws
Name Set of values Law Expectation Variance
Uniform law [[1, n]] P(X = k) =
1
n
n + 1
2
n
2
−1
12
Bernoulli law B(1, p) {0, 1}
§
P(X = 1) = p
P(X = 0) = 1 − p
p p(1 − p)
Binomial law B(n, p) [[0, n]] P(X = k) =
n
k
p
k
(1 − p)
n−k
np np(1 − p)
Poisson l aw N P(X = n) = e
−λ
·
λ
n
n!
λ λ
Continuous laws
Name Set of values D ens i ty f (x) Expectation E(X ) Variance σ
2
Char. function ϕ(ν)
Uniform law [a, b]
1
b − a
χ
[a,b ]
a + b
2
(b − a)
2
12
e
iνb
−e
iνa
iν(b −a)
Normal law R
1
σ
p
2π
exp
−
(x −m)
2
2σ
2
m σ
2
e
imν
e
−σ
2
ν
2
/2
Exponential law R
+
µ
−1
e
−x/µ
µ µ
2
1
1 −iµν
Cauchy law R
a
π
1
a
2
+ (x −m)
2
not defined not def. e
imν−|aν|
χ
2
law R
+
1
2Γ(n /2)
x
2
n
2
−1
e
−x/2
n 2n (1 −2iν)
−n/2
