Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

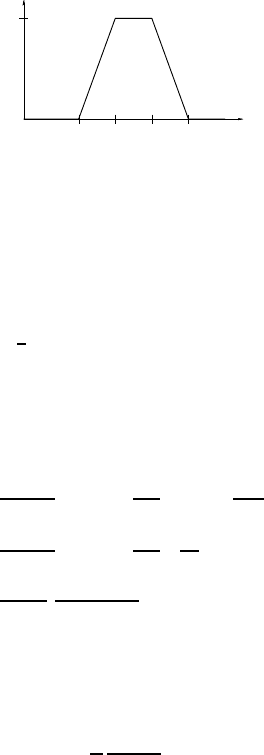
Solutions of exercises 567

The expectation for the mass of the ﬁrst egg is of course 55 g, and the ex pectation for the mass

of the second is 42.5 g. Thus the expectation for the total mass is 97.5 g.

The probability density of the mass of the two eggs togethe r is the convolution

f (x) = f

∗ f

(x) =

+∞

−∞

(t) f

(x − t) dt,

(because, obviously, we can assume that the two masses are independent), which is the function

with the following graph:

0,1

90 95 100 105

The expectation may also be computed from thi s formula: it is equal to

E =

+∞

x f (x) dx = 97.5,

as it should be. The standard deviation satisﬁes

+∞

−∞

(x − E)

f (x) dx = σ

+ σ

Since σ

= 25 /3 and σ

= 25 /6 by immediate computations, we obtain σ

= 25 /2. So the

standard deviation is σ = 5/

2. From the graph, the probability that the mass is at least 100

g is 1/4.

 Solution of exercise 21.11. Let X

and X

be two normal c entered random variables, with

variances σ

and σ

, respectively. By Proposition 20.67, the probability density of the ratio

is given by

g( y) =

2πσ

exp



−

2σ



exp



−

2σ



|t| dt

2πσ

exp



−

2σ



+ y



|t| dt

πσ

/σ

+ y

which is the distribution function of a Cauchy random variable. (To obtain the last line, notice

that the integral to compute is of the type

u(t) u

′

(t) dt.)

 Solution of exercise 21.15. The characteristic function of a C auchy r.v. is given by

f (u) =

iux

+ x

dx = e

−a|u|

Since the characteristic function of the sum of independent random variables is the product

of the characteristic functi o ns of the arguments, we get that the characteristic function of

+ ···+ X

exp



+ ···+ a

) |x|



which does not converge pointwise to the characteristic function of a normal random variable.

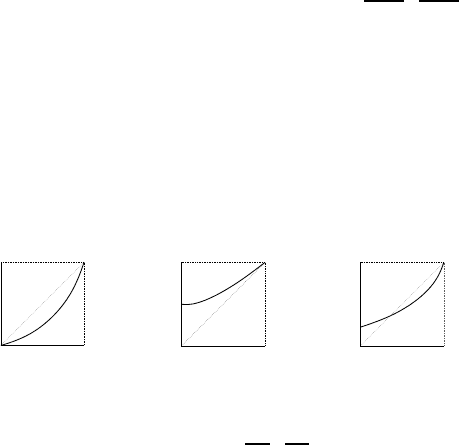
568 Central limit theorem

 Solution of problem 7

i) From the independence of the r.v. X

, we deduce that

k=1

= (G

)

ii) Using the fact that

P(S = n) =

∞

k=0

P(S = n and N = k) =

∞

k=0

P(S

= n and N = k),

we derive

(t) =

∞

n=0

P(S = n) t

∞

n=0

∞

k=0

P(S

= n and N = k) t

∞

k=0

∞

n=0

P(S

= n) ·P(N = k) t

∞

k=0

P(N = k) ·

∞

n=0

P(S

= n) t

| {z }

(t)

∞

k=0

P(N = k)



(t)



= G



(t)



iii) E(S) = G

′

(1) = G

′



(1)



·G

′

(1) = E(N) ·E(X ). A n easy computation yields

Var(S) = G

′′

(1) + G

′

(1) −G

′

(1)

= E

(X ) V (N ) + E(N ) V (X ).

iv) If p

= 1, we have G ≡ 1. If p

< 1, G is a sum of increasing functions, one of whi ch

at least i s strictly increasing.

v) If p

+ p

= 1, then G is afﬁne, with G(0) > 0 and G(1) = 1. If p

+ p

< 1, G is the

sum of convex functions, one of w h ich at least is strictly convex, so it is strictly convex.

vi) The graph o f G may be of one of the following types:

a) : b) : c) :

The equation G(x) = x has two, one, and two solutions, respectively, in the three cases.

vii) Using question ii), we ﬁnd th at G

= G ◦G and then, by inductio n, that

n+1

= G

◦G = G ◦··· ◦G

| {z }

n+1 times

viii) We have x

n+1

= G ◦G ◦··· ◦G(0) = G(x

). In all cases above, there exists an interval

[0, ℓ] on which G(x) ¾ x, and this interval is stable by G, so that the sequence (x

)

n∈N

is increasing and bounded from above by ℓ. Hence, it converges.

ix) We h ave E(Z

n+1

) = G

′

n+1

(1) = G

′



G(1)



·G

′

(1) = E(Z

) · E(Z) since G(1) = 1 and

hence, by induction again, we get E(Z

) = E(Z)

x) (a) There are two cases.

If E(Z) < 1: the curve is as in Figure b) above, which shows that x

→ 1: there

is certain extinction, and E(Z

) → 0.

If E(Z) = 1 and p

> 0: the curve is again of type b), so x

→ 1: there is again

certain extinction and of course E(Z

) = 1.

Solutions of exercises 569

(b) We assume now that E(Z

) > 1. The graph of G is of type c), so that x

→ ℓ ∈

]0, 1]. The probability of extinction is not 1 (there is positive probability because

the particles may all disappear during the ﬁrst steps). Moreover, E(Z

) → +∞:

the reaction is explosive.

 Solution of problem 8

i) We compute the expectation of X

E(X

) = E



k=1

cos θ



k=1

E(cos θ

) =

k=1

2π

cos θ dθ = 0 ,

so X

is centered, and of course so is Y

There only remains to compute σ

) = E(X

) −E(X

)

= E(X

), whic h is given

) = E

(



k=1

cos θ



)

= E

k=1

cos

k6=l

cos θ

·cos θ

= n E(cos

θ) + n(n −1) E(cos θ

·cos θ

Since the variables θ

are independent, we have

E(cos θ

·cos θ

) = E(cos θ

) ·E(cos θ

) = 0,

so we obtain ﬁnally

) = n E(cos

θ) =

2π

cos

θ dθ =

Similarly, we have σ

) = n/2.

ii) To determine whether the variables X

and Y

are correlated or not, we compute the

covariance. We have

Cov(X

, Y

) = E





−E(X

)



−E(Y

)





= E(X

· Y

)

= E

k=1

l=1

cos θ

·sin θ

= n E(cosθ ·sin θ) + n(n −1) E(cos θ · sin θ

′

)

= n E(cosθ ·sin θ) + n(n −1) E(cos θ) E(sin θ

′

) = 0.

Hence X

and Y

are uncorrelated.

However, they are certainly not independent. For instance, if X

= n, we necessari ly

have Y

= 0 (Pierre has walked due east during the ﬁrst n steps), so

P(X

= n and Y = 0) = P(X

= n) 6= P(X

= n) ·P(Y

= 0).

iii) The expectation of R

E(R

) = E(X

+ Y

) = E(X

) + E(Y

) = n.

So the average of the square of the distance after n steps is n. Of course, one can not

deduce that the average distance is

n (which is in fact false).

iv) Since the r.v. cos θ

are independent, have zero expectation and ﬁnite variance, we may

use the central limit th eorem to deduce th at t he distribution of the r.v. X

is c l ose to

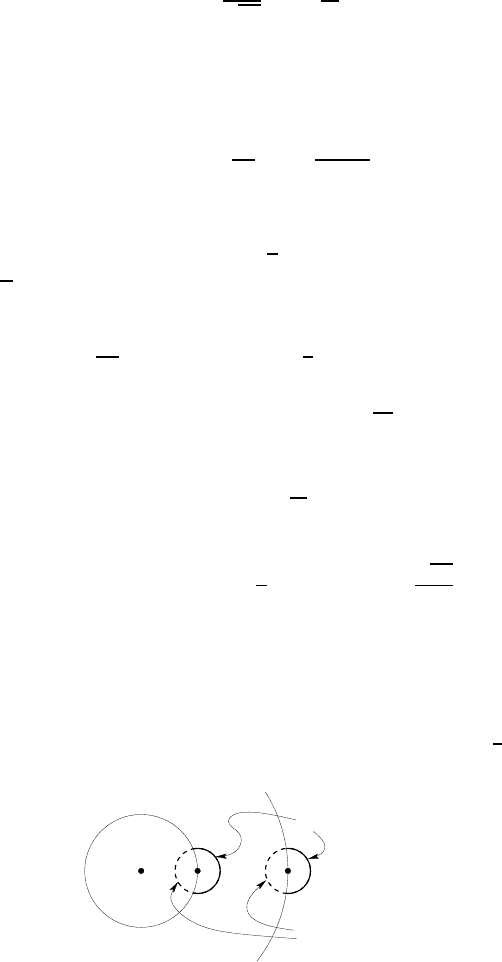
570 C en tral limit theo rem

that of a normal centered r.v. with the same variance n/2. The density probability for

such a random variable

(x) =

nπ

exp



−



Of course, the same is true for Y

, which can be approximated by

which also has

probability density f

Since X

and Y

are uncorrelated, it is natural to assume that

and

are also

uncorrelated, and therefore they are independent, so that the joint probability density

(x, y) ≈

nπ

exp



−

+ y



v) The distribution fu nct ion H

(r) of t h e r.v. R

is given by

(r) = P(R ¶ r) =

ZZZ

B(0 ; r)

(x, y) dx dy,

where B(0 ; r) is the closed disc of radius r centered at the origin. Using the approxi-

mation above for the density and polar coordinates, we obtain

(r) ≈

nπ

2π

−ρ

ρ dρ dθ =

−ρ

ρ dρ

−u/n

= 1 −e

−r

The probability density of R

is therefore

(r) = H

′

(r) ≈

2 r

−r

vi) Finally, the expectation of R

is computed by

E(R

) =

+∞

r h

(r) dr ≈

+∞

−r

dr =

nπ

Notice that the distance to the origin increases wit h time (rather slowly, compared

with n).

The following heuristic reasoning suggests an explanation: the p robability of getting

farther from the pub is larger than the probability of getting c loser to the pub, as can

be seen in the picture below: t he circular arc describing the values of θ leading to

an increase of the distance is larger than the other (in fact, a simple computation

shows that the difference between the length of the two arcs if of order 1/

r, whic h is

consistent with the result obtained).

going farther

going closer

pub

What a beautifu l argument! Unfortu nately, it comes somewhat after the fact, and it

has limits. Indeed, a one-dimensional random walk is also characterized by a distance

Solutions of exercises 571

to the origin E(R

) proportional to

n, whereas the probability of getting closer is the

same as the probability of going further from the origin.

The conclusion to draw from this tale: beware nice heuristic reasonings; sometimes,

they are but webs of lies and deceit.

Appendix

Reminders conc erning

topology and normed

vector spaces

A.1

Topology, topological spaces

Since topology is probably not well known to many physicists, we recall a

few elementary deﬁnitions. At the very least, they a re very us eful for stating

precisely properties of continuity and convergence in sets which are more

complicated t han R.

DEFINITION A.1 (Open sets, neighborhoods) Let E be an a rbitrary set. A

topology on E is the data of a set O of subsets of E, called the open subsets

of E (for the given topology), which satisfy the following three properties:

i) ∅ ∈ O and E ∈ O;

ii) for any set I, and any family (A

)

i∈I

of open subsets, the union

i∈I

is also an open set (any union of open sets is open);

574 Topology an d normed vector spaces

iii) for any n ∈ N and any ﬁ nite family (A

, . . . , A

) ∈ O

of open sets,

the intersection

i=1

∈ O is open (any ﬁnite intersection of open sets is

open).

Finally, a neighborhood V of a point a ∈ E is any subset V ⊂ E

containing an open set Ω ⊂ V such that a ∈ Ω.

If a set E is given a topology O, then the pair (E, O), or E itself by abuse

of notation, is called a topological space.

Remark A.2 If E is a metric space, that is, a set on which a distance function is deﬁned, the

distance can be used to deﬁne a metric topology, using the open balls deﬁned by the distance. In

partic u l ar this is the case for normed vector spaces, whi ch we will discuss separately below.

Using th e notion of open set, the continuity of a map can be deﬁned.

DEFINITION A.3 (Continuity of a m a p) Let (E, O) and (F , O

′

) be two topo-

logical spaces. A map f : E → F is continuous if, for any open s et Ω ⊂ F ,

the inverse image f

−1

(Ω) =



x ∈ E ; f (x) ∈ Ω



is an open set in E, tha is,

if f

−1

(Ω) ∈ O for any Ω ∈ O

′

Remark A.4 This deﬁniti on should be compared with t h at of a measurable map between two

measurable spaces (see Deﬁnition 2.21 on page 62).

DEFINITION A.5 (Dense subset) Let (E, O) be a topological s pace. A subset

X ⊂ E is dense in E if, for any a ∈ E and any V which is a neighborhood

of a in E, V meets X , that is, V ∩ X 6= ∅.

DEFINITION A.6 (Connected sets) A topological s pace (E, O) is connected if

it is not the union of two nonempty disjoint open sets: it is not possible to

ﬁnd A and B such that

X = A ∪ B with A ∈ O, B ∈ O, A 6= ∅, B 6= ∅, A ∩ B = ∅.

A subset X ⊂ E is connected if (X , O

) is connected, where the induced

topology O

on X is the topology with open sets of the form U = A ∩ X

for some A ∈ O.

In other words, the topological s pace is connected if it is “in one piece.”

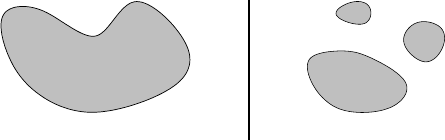
Example A.7 Below are pictures of two sets in th e plane; the set (a) is connected, while (b) is

not.

(a) (b)

Topology, topological spaces 575

Be careful not to mix connected and convex. The ﬁrst is a purely topological

notion, the second is geometr ic.

DEFINITION A.8 (Convexity) A s ub set X in a vector space or in an afﬁne

space is convex if, for any points A, B in X , the line segment [A, B] is

contained in X . (The segment [A, B] is deﬁned as the set of points λA +

(1 − λ)B, for λ ∈ [0, 1], and this deﬁ nit ion requires a vector space, or afﬁne

space, structure.)

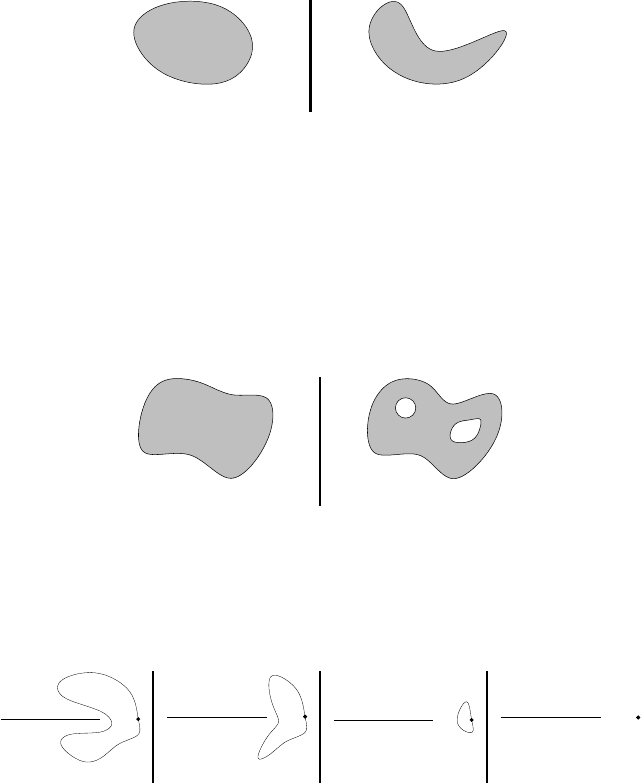
Example A.9 Al l vector space s are convex. Below are examples (in the plane) of a convex set (a)

and a nonconvex set (b); note that both are connected.

(a) (b)

DEFINITION A.10 (Simply connected set) A topological space (E, O) is sim-

ply connected if any closed loop inside E may be deformed continuously to

a t rivial constant loop (i.e., all loops are homotopic to zero).

A subset X ⊂ E is simply connected if the topological space (X , O

) is

simply connected.

In the special case E = R

(or E = C), a subset X ⊂ R

is simply connected

if “there is no hole in X .”

Example A.11 Still in the pl ane, the set in (a) is simply c onnected, wh ereas the set in (b) is not.

Again both are connected.

(a) (b)

Example A.12 Let X be the complex plane minus the origin 0; t h en X is not simply connected.

Indeed, any loop turning once completely around the origin cannot be retracted to a single point

(since 0 is not in X !).

On the other hand, the complex plane minus a half-line, for instance, the half-line of

negative real numbers (i.e., C \R

−

) is simply connected. Below are some illustrations showing

how a certain loop is deformed to a point.

Step 1 Step 2 Step 3 Step 4

576 Topology and normed vector spaces

Example A.13 A torus (the surface of a doughnut) is not simply connected. In the picture

below one can see a closed loop which can not be contracted to a single point.

Example A.14 The unit circle U = {z ∈ C ; |z| = 1} in the complex plane is not simply

connected.

An important point is th at connected and simply-connected sets are pre-

served by continuous maps.

THEOREM A.15 The image of a connected set (resp. simply connected set) by a con-

tinuous map is connected (resp. simply connected).

DEFINITION A.16 (Compact sets) An open covering of a topological space

K is any family of open sets (U

)

i∈I

such that K is the union of the sets U

[

i∈I

= K .

The topological space K is compact if, from every open covering of K ,

one can extract a ﬁnite subcovering, i.e., there exist ﬁnitely many indices i

,. . . ,

, such that

[

j=1

= K .

A subset X ⊂ K is compact if it is compact with the induced topology.

The deﬁnition of compact spaces by this property is mostly of interest to

mathemat icians . I n metric spaces (in particular, in normed vector spaces), this

property is equivalent with the following: from any sequence (x

)

n∈N

with values

in K , one can extract a subsequence that converges in K .

Moreover, in any ﬁnite-dimensional normed vector space, compact sets are

exactly those which are closed and bounded (see Theorem A.42).