Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Centra l limit theorem 557

A child prodigy, Carl Friedrich Gauss (1777—1855), son of an arti san,

entered the University of Göttingen at eighteen. He made contri-

butions to astronomy (rediscovering Ceres, which lesser minds had

managed to lose in the ﬁrmament, by means of orbit computations)

and geodesy. With Wilhelm Weber, he created the theory of mag-

netism. However, his greatest discoveries were in mathematics. At

nineteen, he proved that the regular seventeen-sided polygon can

be constructed with straightedge and compass, and further gener-

alized this result.

One of the greatest among arithmeticians (he

introduced congruences, for instance), he also lai d th e foundation

of differential geometry, deﬁning in particular the Gauss curvature

of a surface. He was named “th e prince of mathematicians.”

The fundamental result (in particular, in many physical applications) is

that the s uccess ive sums of the terms of a sequence of independent, identi-

cally distr ibuted random varia bles (square integrable), will always converge (in

distribution) to a Gaussian random variable, after an appropriate scaling. In

particular, in statistical physics, this is why many measurable quantities can be

expressed by the computation of a moment of Gaussian varia bles. Problem 8

gives the ex ample of a simple problem of a random walk in t he plane.

The theorem stating this fact is called the “central limit theorem.”

In the

case of Bernoulli random variables (heads or tails), it was stated and proved

by Abraham de Moivre.

We begin by recalling the main facts conerning th e Gaussian or normal

distribution, which is so essential in this result.

DEFINITION 21.8 (Normal distribution) The normal distribution with mean

m and standard deviation σ > 0, or Gaussian distribution with mean m and

standard deviat ion σ > 0, denoted N (m, σ

), is the probability distribution

on R with density given by

m ,σ

(x) =

2πσ

exp



−

(x −m)

2σ



A normal distribution of the type N (0, σ

) is called a centered normal

distribution.

The reader will easily check that the characteristic function of the normal

distribution N (m , σ

) is given by

m ,σ

(u) = e

ium

exp



−



, in particular, Φ

0,σ

(u) = e xp



−



Translated lierally from the German, where a more suitable translation would have been

“fundamental limit theorem (of probability theory).”

558 Central limit theorem

Paul Lé v y (1886—1971), son and grandson of mathematicians, stud-

ied at the École Polytechnique, then at the École des Mines, where

he became professor in 1 913 . Hadamard, one of his teachers,

asked him to collect the works of René Gâteaux, a young math-

ematician killed at the beginning of the First World War. After

doing this, Lévy developed the ideas of Gâteaux on differential

calculus and functional analysis. At the same time as Khint-

chine, he studied random variables, and in particular the prob-

lem of t he convergence of sequences of random variables. He

also improved and expanded considerably the results of Wiener

concerning Brownian motion. He was also i nterested in partial

differential equations and the use of the Laplace transform.

THEOREM 21.9 (Central l imit theorem) Let (X

)

n∈N

∗

be a sequence of indepen-

dent, identically distributed random variables with ﬁnite expectation m and ﬁnite

variance σ

. Let

def

+ ···+ X

and Z

n(Y

−m).

Then the sequence (Z

)

n∈N

∗

converges in distribution to the centered normal distribu-

tion N (0, σ

). In other words, we have



−nµ

< x



−−−→

n→∞

N (x) =

−∞

−t

dt.

for all x ∈ R.

Proof. Let S

def

= X

+ ··· + X

. We can compute the characteristic function of Z

namely:

(u) = E



iu Z



= E



−i u



= e

−i um





= e

−i um







where the last relation follows from the independence of the r.v. X

and from Theo-

rem 20.59.

We now perform a Taylor expansion of Φ





to order 2, using th e fact that

′

(0) = iE( X ) and Φ

′′

(0) = −E(X

and this yi elds Φ





= 1 + i

m −

E(X

) + o





Inserted in the preceding relation, this implies that

(u) = exp



−i

+ o







so the characteristic functions of Z

converge pointwise to that of the normal distribu-

tion. This turns out to be enough to imply the result (which is not too surprising, since

the characteristic function of an r.v. determines its distribution uniquely, as recalled

earlier), but the proof of this implication involves the continuity theorem of Paul Lévy

and is by no means easy.

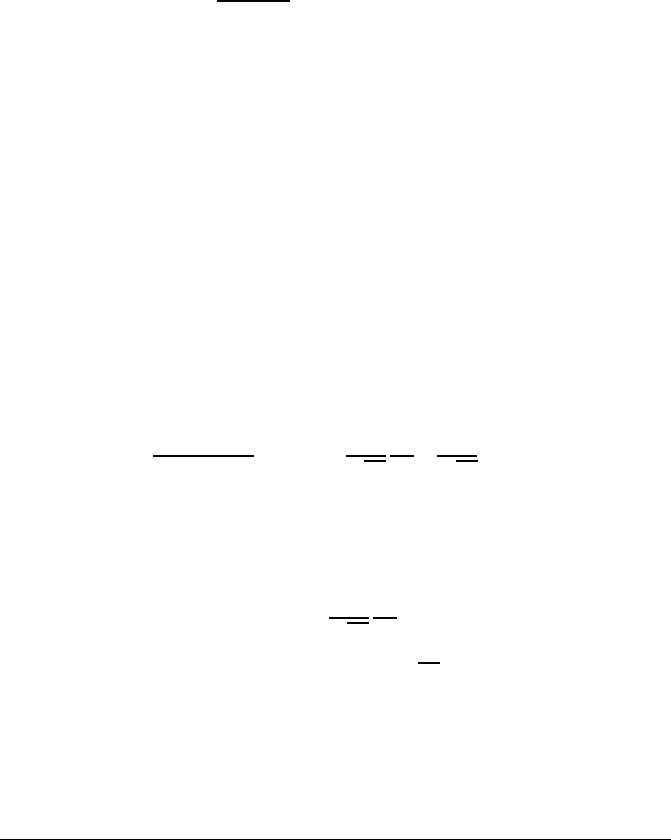
Centra l limit theorem 559

Remark 21.10 The condition that the variance Var(X

) be ﬁnite is necessary. Exercise 21.15

on page 562 gives a counterexample to the central limit theorem when this assumption is

not satisﬁed. It should be mentioned that non-Gaussian processes are also very much in current

fashion in probability theory.

Application

Consider a piece of copper, of macroscopic size (electrical wir ing, for instance).

Because of thermal ﬂuctuations, the average velocity of a conducting electron

in this copper wire is

T /m, that is, of the order of 10

m · s

−1

, or tens

of thousands of kilometers per second! Yet, the copper wire, on a table, does not

move. This is due to th e fact that the velocities of the electrons (and of nuclei,

although th ey are much slower) are randomly distributed and “cancel” each

other. How does this work?

Let N be t he number of conducting electrons in the wire. We a ssume that

the wire also contains exactly N atoms,

and we will denote by m and M ,

respectively, the masses of the electrons and atoms. You should ﬁrst check

that the velocity of atoms is neg ligible in this problem.

We denote by X

the random variable giving the velocity (at a given time)

of the n- th electron. What is called the “average velocity” is not the expectation

of X

, since (in the absence of an electric ﬁeld), the system is isotropic a nd

E(X

) = 0. In fact, the “average velocity” is best measured by the standard

deviation of the velocity σ(X

What is then “average velocity” (the standard deviation of the velocity) of

the whole wire? Since the number N of atoms and electrons is very large (of

the order of 10

), we ca n write

Y =

N(m + M )

n=1

≈



n=1



and the term in parentheses is close to a centered gaussian with var iance σ

by the central limit theorem.

The standard deviation of Y is therefore very close to

σ(Y ) =

σ.

Notice the occurrence of the famous ratio 1/

N, which is characteristic of

the ﬂuctuations of a system w ith N particles. In the present case, this reduces

the “average velocity” of the set of electrons to 1.5 ·10

−7

m ·s

−1

Depending on the metal used, it may not be N, but rather N /2 or N /3; however, the

principle of the calculation remains the same.

560 Central limit theo rem

EXERCISES

Combinatorics

 Exercise 21.1 All 52 c ards in a pack of cards are dealt to four players. What is the probability

that each player gets an ace? Does the probability change a lot when playing algebraic wh ist?

(Recall that algebraic whist is played with a pack of 57 cards.)

Hint: Compute ﬁrst, in general, the number of ways of subdividing n objects into k

subsets containing r

, . . . , r

objects, respectively.

 Exercise 21.2 Take a pack of n cards, and deal them face up on a table, noting the order the

cards come in. Then shufﬂe the pack thoroughly and deal them again. What is the probability

that at least one card occurs at the same position both times? Does this probability have a

limit as n goes to inﬁnity?

It is amusing to know that th is result was used by con-men on Mississippi steamboats, who

exploited the passengers’ intuitive (wrong) assumption that the probability would be much

smaller than it actually is.

Conditional probabilities

 Exercise 21.3 Mrs. Fitzmaurice and Mrs. Fitzsimmons discuss their respective children

during a plane trip. Mrs. Fitzmaurice says: “I have two children, let me show you their

pictures.” She looks in her bag, but ﬁnds only one picture: “This is my lit tle Al icia, playing

the piano last summer.”

What is the probability that Alicia has a brother?

 Exercise 21.4 A religious sect practices population control by means of the following rules:

each family has chi l dren (made in the dark) until a boy i s born. Then, and only then, they

abstain for the rest of their days. If the (small) possibilit y of twins is neglected, and knowing

that with ou t any control, about 51% of babies are boys, what will be the percentage of males

in the community?

Same question if each family al so limits to twelve the total number of children it can have.

 Exercise 21.5 A new diagnostic test for a lethal disease has been devised. Its reliability is

impressive, says the company producing it: clinical trials show that the test is positive for

95% of subjects who have the disease, and is negative for 95% of subjects who do not have it.

Knowing that this disease affects roughly 1% of the populatio n, what probability i s there that

a citizen taking the test and gett ing a positive result will soon end up in eternal rest in the

family plot?

 Exercise 21.6 Another amusing exercise. The other day, my good friend J.-M. told me that

he knows someone to whom the most amazing thing happ ened. This other person was just

thinking of one of his former relations, who he had not thought about for 10 years, and the

very next day he learned the person had just died, at the same time he was thinking of him!

(Or maybe withi n ten minutes.)

What should one think of this “extraordinary” (rigorously true) fact? Does this kind of

thing happen often, or do we have here an example of ESP (Extra-Sensory Perception, for the

uninitiated)?

 Exercise 21.7 In 1761, Thomas Bayes, Protestant theologian, leaves for ever t his vale o f tears.

He arrives at the Gates of Heaven. But there is not much room left, and anyway God is a strict

Presbyterian and Bayes, unluckily for him, was a Nonconformist minister. However, St. Peter

Exercises 561

gives him a c h ance: Bayes is shown three identical doors, two of which lead to Hell and only

one to Heaven. He has to choose one. With no information available, Bayes selects one at

random. But before he can open it, St. Peter — who is good and likes mathematicians — stops

him. “Wait, here is a clue,” he says, and opens one of the two remaining doors, which Bayes

can see leads to Hell.

What should Bayes do? Stick to his door, or change his mind and se lect the ot her unopened

door?

Expectation, s tan dard deviation

 Exercise 21.8 W h en a students hands in an exam paper, it will get a grade corresponding

roughly to the objective quality level of the paper. However, because of random pe rturbations

of the grader’s environment (did he eat well at lunch, is his cat purring on his knees,...), the

actual grade is really a random variable, with expectation equal to the “objective” grade m, and

with standard deviation σ = 2, say, for a paper graded out of 20 points.

To get a more exac t result, it is possible to ask N different graders to look at the paper

and then average their respective grades, each of which is a random variable with the same

distribution, with expectation m and standard deviation σ.

Denote by X

, . . . , X

the corresponding random variables for each grader, and let S

+ ···+ X

)/N be the average of their grades. What is the expectation of S

? What is its

standard deviation?

How many correctors are needed so that the probability is at least 0.8 that the average grade

corresponds to the exact grade, within half a point? Same question if the standard deviation σ

is only half a poi nt. Do you have any comments about t h e results?

 Exercise 21.9 Solveig wants to make a chocolate cake. The recipe states that “two large eggs

(100 g)” are needed. But she only has two eggs from two different brands. The ﬁrst package

says the eggs inside are “large” (between 50 and 60 g, with mass uniformly distributed), and the

second says the eggs are “medium” (between 40 and 45 g wit h uniform distribution). What is

the probability density of the total mass of the two eg gs? What is the average and standard

deviati o n of this mass? What is the probability that the mass is greater than 100 g?

Covariance

 Exercise 21.10 Let (X

)

n∈N

∗

be a sequence of random variables, pairwise independent, with

the Bernoulli distribution.

with parameter p. Let Y

= X

n+1

for n ∈ N

∗

1. Find the distribution of Y

2. Compute Cov



, Y

n+k



for n, k ∈ N

∗

3. Let

i=1

for n ∈ N

∗

. Show that the sequence (S

)

n∈N

∗

converges in probability to the determinist

(constant) random variable p

This version of the classical “Monty Hall paradox” was suggested by Claude Garcia.

Recall that a Bernoulli distribution with parameter p is the distribution of a random

variable which takes the value 1 with probability p and 0 with probability 1 − p.

562 Central limit theorem

Sum and product of r.v.

 Exercise 21.11 Show that the ratio of two independent centered normal random variables

is a r.v. with a Cauchy distribution; recall that this means that for some a ∈ R, the probability

density is

f (x) =

+ x

 Exercise 21.12 Let X be Y be two independent random variables, such that X has a Poisson

distribution with parameter λ and Y has a Poisson distribution with parameter µ, where

λ, µ > 0. Let p

= P(X = n) and q

= P(Y = n ) for n ∈ N.

i) Show that Z = X + Y has a Poisson distribution with parameter λ + µ.

ii) Let k ∈ N. Compute the conditional probability distribution of X knowing that

Z = k.

iii) Let W = X − Y . Compute the expectation and the variance of W .

Convergence

 Exercise 21.13 A player ﬂips two coins B

and B

repeatedly according to the following

rule: if ﬂipping whichever coin is in his hand yields tail s, switch to the other coin for the next

toss, otherwise continue with the same. Assume that tails is the outcome of ﬂipping B

with

probability p

= 0.35, and of ﬂipping B

with probability p

= 0.4. Let X

be t h e random

variable equal to 1 if the player is ﬂipping coin B

at the k-th step, and equal to 0 otherwise.

Let

(k) = P(X

= 1), h

(k) = P(X

= 0), and H (k) =



(k)



i) Show that H (k + 1) = M · H (k), where M is a certain 2 × 2 matrix. Deduce that

H (k) = M

H (0), where H (0) is the vector corresponding to the start of the game.

ii) Diagonalize the matrix M . Show that as k tends to inﬁnity, H (k) co nverges to a vector

which is independent of the initial conditions. Deduce that the sequence (X

)

k∈N

converges almost surely to a random variable, and write down the distribution of this

random variable.

 Exercise 21.14 Let (U

) be a sequence of identically distributed independent random vari-

ables such that

P(U

= 1) = p, P(U

= −1) = q = 1 − p with p ∈ [0, 1] .

Deﬁne a sequence of random variables V

by V

i=1

. Find the distribution of V

, then

show that (V

) converges in distribution to a random variable V , and ﬁnd the corresponding

distribution (it may be helpf u l to compute the expectation of V

 Exercise 21.15 (C o unterexample to the central limit theorem) Show that if X

and X

are

Cauchy random variables with parameters a and b, respectively (see Exercise 21.11), then the

random variable X

+ X

is a Cauchy random variable with parameter a + b (compute the

characteristic function of a Cauchy random variable). What conclusion can you draw regarding

the central limit theo rem?

Exercises 563

PROBLEMS

 Problem 7 (Cha in reaction) Let X and N be two square integrable random variables taking

values in N. Let (X

)

k¾1

be a sequence of independent random variables with the same distri-

bution as X . Assume further that N is independent of the sequence (X

)

k¾1

. Let G

and G

denote the generating functions of X and N . For n ¾ 1, let

k=1

Finally, let S be deﬁned by

∀ω ∈ Ω S (ω) =

N (ω)

k=1

(ω).

i) For n ∈ N, compute the generating function G

of S

, in terms of G

ii) Show that G

(t) = G



(t)



= G

◦G

(t) for any t ∈ [−1, 1].

iii) Compute E(S ) and V (S ) in terms of the expectation and the variance of X and N .

—

Consider now a reacti on (for instance, a nuclear reaction) oc curring in a certain

environment. Time is measured by an integer n ¾ 0 for simplicity. A particle (ti me 0)

comes into the environment, is absorbed, and produces new particles (time 1). In turn,

each new particle generates ne w particles at the next instant.

We denote by p

the (constant) probability that a particle creates no other particle,

and for k ∈ N

∗

, we let p

be the probability that it creates exactly k particles. Let

∀t ∈ R G(t) =

∞

k=0

Finally, let Z

be the random variable which is the total number of particles at time k,

and let x

be the probability that no particle survives at time n (end of the reaction):

∀n ∈ N

∗

= P(Z

= 0).

iv) Find G when p

= 1. We now assume that p

< 1. Show that G is strictly increasing

on [0, 1].

v) Find G if p

+ p

= 1. Assuming now th at p

+ p

< 1, show that G is convex.

vi) In the following cases, ﬁnd the number of solutions to the e quation G(x) = x:

a) p

= 0 ; b) 0 < p

< 1 and G

′

(1) ¶ 1 ; c) 0 < p

< 1 and G

′

(1) > 1

vii) Find a recurrence relation expressing the generating function G

n+1

of Z

n+1

in terms of

the generating function G

of Z

and of G.

viii) Still under the condition 0 < p

< 1, ﬁnd a recurrence relation between x

and x

n+1

Show that the sequence (x

)

k∈N

is increasing, and deduce that it converges to a limit ℓ

such that 0 < ℓ < 1.

ix) Show that E(Z

) = E(Z

)

x) Show from the preceding results that:

(a) if E(Z

) ¶ 1, then the probability that the reaction stop before time n converges

to 1 as n tends to inﬁnity;

(b) if E(Z

) > 1, then this probability converges to a limite 0 < ℓ < 1. What should

we expect from the reaction? What are your c o mments?

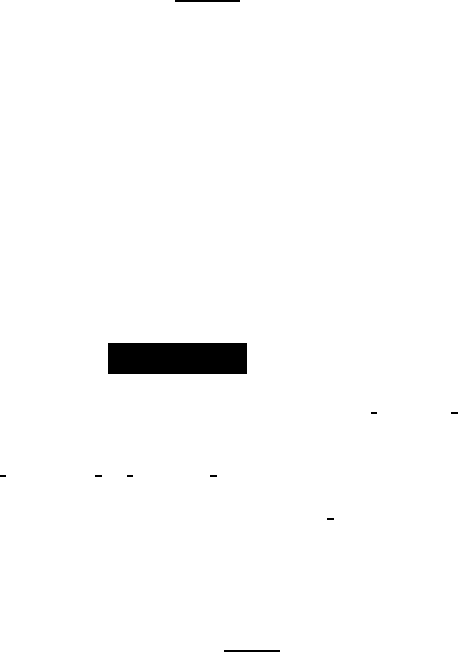
564 Central limit theorem

 Problem 8 (Random walk in the plane) Consider a plane named P , a point named O wh ich

serves as origin for some cartesian coordinate system on P , and a drunk mathematician named

Pierre who, having proﬁted extensively from his pub’s extensive sel ection of si ngle malt whiskey,

leaves the afore mentioned pub (located at the origin O) at time t = 0 to walk home. Each

second, he make a single step of ﬁxed unit length, in a random direction (obstacles, constables,

and ot h er mishaps are c o nsidered negligible).

Let X

and Y

be t h e r.v. co rresponding to the x- and y-coordinates of Pierre after the

n-th step, and let θ

denote the angle (measured from the x-axis) giving the direction following

during the n-th step. Thus we have

k=1

cos θ

and Y

k=1

sin θ

We assume that the θ

are independent random variables uniformly distributed between 0 and

2π.

The objective is to study the r.v.

+ Y

representing the distance from the pub.

i) Show that the r.v. X

and Y

have expectation zero, and compute their variance.

ii) Are X and Y correlated? Are they independent?

iii) What is the expectation of R

iv) Explain why it is reasonable to assume that for large n, the joint distribution of (X

, Y

)

may be approximated by the joint distribution of a pair of independent centered normal

distributions. (Use th e fact that uncorrelated gaussian variables are in fact independent.)

What is the (approximate) probability density of the pair (X

, Y

v) Deduce the (approximate) distribution function, and then the probability density,

of R

vi) Finally, ﬁnd an approximation for the expectation E(R

SOLUTIONS

 Solution of exercise 21.3. The probability that Alicia has a brother is

, and not

Indeed, among families with two chi l dren, about 25% have two boys, 25% have two girls,

and therefore 50% have one each. Since we know that there is at least one girl, the probability

of having two girls is

divided by

, whic h is

If Mrs. Fitzmaurice had distinguished between her children (saying, for instance, “Here

is my older child at the piano”), the probability would have been

. (Among those families

whose ﬁrst child is a girl, there are 5 0% where the second i s a girl.)

 Solution of exercise 21.2. Let A

denote the event which is “the i-th card is at t he same

place both times.” It is easy to see that P(A

) = 1/n, that P(A

∩ A

) = 1/n(n −1) for i 6= j

and that more generally

P(A

∩···∩ A

) =

(n −k )!

when all indices are distinct. Using the Poincaré formula, t h e probability of the event B: “at

least one of the cards is at the same p l ace both ti mes” is

P(B) = P

[

i=1

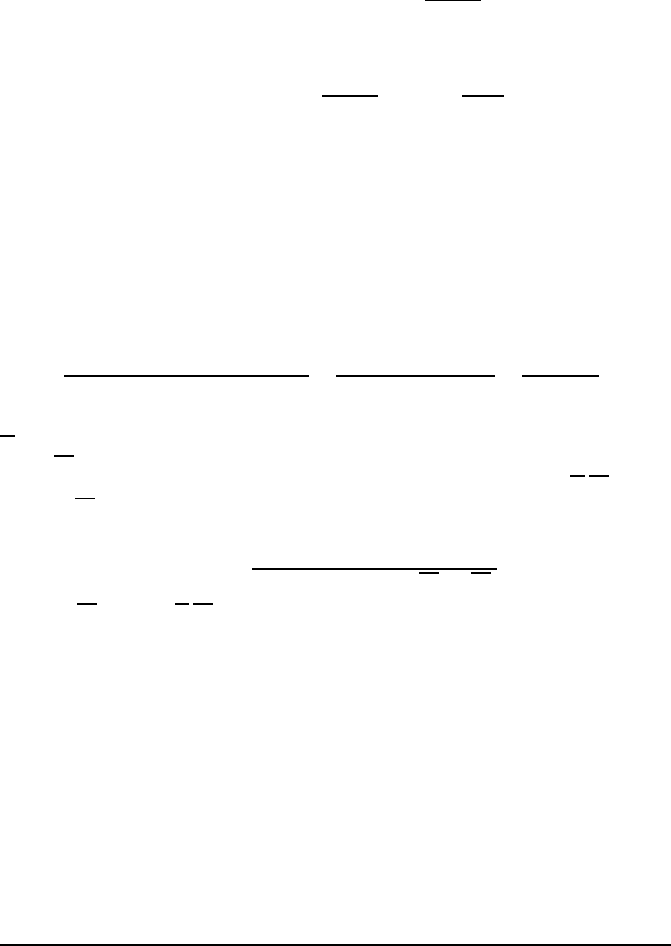
Solutions of exercises 565

and i s the refore equal to

P(B) =

k=1

(−1)

k+1

1¶i

<···<i

¶n

(n −k )!

There are





distinct k-t u ples in the sum, and we obtain

P(B) =

k=1

(−1)

k+1

(n −k )!

= 1 −

k=0

(−1)

This probability converges to 1 −1/e (this is t h e beginning of the power series expansion for

−1

), or roughly 63%.

 Solution of exercise 21.4. The probability hasn’t c hanged: there are still 51% of baby boys

in the community.

This is easy to ch eck: notice that every family has e xactly one boy; t h ose with two children

have exactly one boy and one gi rl, tho se with three have one boy and two girls, etc. The families

with n children have one boy and n −1 girls.

Let P (n) be the probability that a family has n children. We have of course P (n) = pq

n−1

with p = 0.51 the probability that a baby is a boy, and with q = 1 − p.

The proportion of boys is then given by

t =

P (1) + P (2) + ···+ P (n) + ···

P (1) + 2P (2) + ···+ nP (n) + ···

p(1 + q + q

+ ···)

p(1 + 2q + 3q

+ ···)

p/(1 − q)

= p.

 Solution of exercise 21.5. Let P denote the event “the result of the test is positive,” and let

P be the opposite event. Let M denote the event “the person taking the test has the disease,”

and let M be it s opposite.

From the statement of the problem, we know that P(P |M ) = 0.95 and that P(P |M ) = 0.95.

Since (M, M) is a partition of the sample space (either a person has the disease , or not), by

Bayes’s formula, we have

P(M|P ) =

P(P |M) ·P(M)

P(P |M) ·P(M) + P(P |M) ·P(M)

With P(P |M) = 1 − P(P |M) = 0.05, the probability of having the disease when the test is

positive is “only” around 16%.

 Solution of exercise 21.6. Before making computations, two comments are i n order. Saying

that the story is tru e does not mean that premonition really occurred, but that this is how the

story was told. Moreover, you are entit l ed to disbelief — it is not because it is printed, with “True

Story” explicitly stated, even in Bold Face, that it is really true. For this t ype of debate, this is

an important remark.

What is the probability for one given person, whom I think about once in ten years, that I

will do so within ten minutes of his death? Let’s spread out death on an interval of 80 years,

or roughly 42 million minutes, so that we can guess that the probability is roughly one out of

4.2 million.

I estimate that I know, more or less, roughly a thousand persons (including those I only

think about only once ten or twenty years); there may therefore be about one million people

who know someone I know.

Hence it is not only possible, but in fact rather unsurpri sing,

that someone could tell me such a story!

This may be of the wrong order of magnitude, si nce my acquaintances each have, among

the people they “know” (those they only think about once in ten years, including people

known only by name, actors, and so on) rather more than a thousand individuals. On the

other hand, t he sets are cert ainly not disjoint. Any ﬁner estimate would be interesting.

566 Central limit theorem

This does not mean that ESP does not exist; only that there is no need here to invoke a

paranormal ph enomenon in order to explain what happened.

 Solution of exercise 21.7. Let us assume that door A leads to Heaven, and doors B and

C to Hell. If Bayes had chosen A, Saint Peter will open B or C for him; changing hi s mind

means Bayes will go to Hell.

If Bayes had chosen door B, Saint Peter, necessarily, must open door C for him (since he

opens a door leading to Hell), so if Bayes changes his mind, he will go to Heaven. The same is

obviously tru e if Bayes had chosen door C .

Therefore, independently o f his original choic e, if Bayes changes his mind after Saint Peter

has shown him one door, this change of mind will swit ch his destination from the one ﬁrst

chosen. This means the probability that Bayes will go to Heaven is now 2/3 and the probability

of going to Hell is now 1/3.

Conclusion: well, this rather depends on wh at Bayes really wants — does he want to spend

the rest of his (eternal) life hearing angels play the harp, or is he more interested i n playing

roulette w ith the devils?

 Solution of exercise 21.8. This exercise is a simple appli cation of the Bienaymé-Tchebychev

inequality. The goal is that the probability of the grade being too far from m be less than 0.2.

Consider the random variable X

+ ···+ X

. It has expectation N m, and S

has expectation

m. The variance of X

+···+X

, on the other hand, is equal to N σ

, as can be seen by looking

at the centered random variables X

′

= X

−m, with zero expectation and standard deviation σ.

The variance of the sum X

+ X

is simply E((X

′1

+ X

′2

)

) = E((X

′

)

) + E((X

′

)

) = 2σ

and similarly by induction for the sum of N random variables (since every crossed term has

expectation equal to zero). Hence the standard deviation of X

+ ··· + X

N σ and that

of S

= (X

+ ···+ X

)/N i s σ/

We are looking for a value of N such that



−m| ¾



¶ 0.2.

The Bienaymé-Tchebychev inequality states that we always have



−m| ¾

ǫσ



¶ ǫ

So we need 1/ǫ

= 0, 2, or ǫ =

5, and it then sufﬁces that

5σ

or N = 4 × 5 ×σ

= 20 σ

to be cert ain that th e desired inequality holds.

For a value σ = 2, one ﬁnds N = 80!!! This is rather unrealistic, considering the average

budget of a university. If the graders manage to grade very consistently, so that their individual

standard deviation is σ =

, it will be enough to take N = 5. This is still a l ot but will

provoke fewer cardiac incidents among university administrators.

However, notice that those estimates are not optimal, because the Bienaymé-Tchebychev in-

equality can be reﬁned sig niﬁcantly if the distribution o f the random variables X

is known (it

is only in itself a worst-case scenario). We know that 80 graders will achieve the desired g o al ,

independently of the distribution (given the expectation and standard deviation), but it is very

likely that a smaller number sufﬁces.

 Solution of exercise 21.9. The probability densities of the masses of the ﬁrst and second

egg, respectively, are

(x) =







0 i f x /∈ [50, 60] ,

if x ∈ [50, 60] ,

and f

(x) =







0 if x /∈ [40, 45] ,

if x ∈ [40, 45] .