Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Analytic signals 367

An example of the use of analytic signals is given by a light signal, charac-

terized by its real amplitude A

(R)

(t). We have

(R)

(t) =

+∞

−∞

(R)

(ν) e

2πiνt

dν,

where A

(R)

(ν) is the Fourier transform of A

(R)

(t). However, since A

(R)

(t) is real,

it is also possible to write

(R)

(t) =

+∞

a(ν) cos



ϕ(ν) + 2πiν t



dν,

where for ν > 0 we denote 2A

(R)

(t)(ν) = a(ν) e

iϕ(ν)

with a and ϕ real.

The imaginary signal as sociated to A

(R)

is of course given by

(I)

(t) =

+∞

a(ν) sin



ϕ(ν) + 2πiν t



dν,

and the analytic signal is

A(t) =

+∞

a(ν) e

iϕ(ν)

2πiνt

dν.

The quantity a(ν) = 2



(R)

(ν)



has the following interpretation: its square

W (ν) = a

(ν) is the power spectrum, or spectral density of the complex sig-

nal A (see Deﬁnition 13.26 on the next page). This complex spectral density

contains the energy carried by t he real signal, a nd an equal amount of energy

carried by the imaginary signal. The total ligh t intensity ca rried by the real

light signal is then equal to

E =

+∞

W (ν) dν =

+∞

−∞

(R)

(ν)|

dν,

namely, half of the total complex intensity (the other half is of course carried

by the imaginary signal).

368 Physical applications of the Fourier transform

13.5

Autocorrelation of a ﬁnite energy function

13.5.a Deﬁniti on

Let f ∈ L

(R) be a square integrable function. We know it has a Fourier

transform

f (ν).

DEFINITION 13.25 A ﬁnite energy signal is any function f ∈ L

(R). The

total e nergy of a ﬁnite energy signal is

def



f (t)



dt.

The Parseval id ent ity st ates that



f (t)



dt =



f (ν)



dν,

so we can interpret



f (ν)



as an energy density per frequency interval dν.

DEFINITION 13.26 The spectral density of a ﬁnite energy signal f is th e

function ν 7→



f (ν)



In optics and quantum mechanics, for instance, the autocorrelation func-

tion of f is often of interest:

DEFINITION 13.27 Let f be a square integrable function. The autocorrela-

tion function of f is the function Γ = f ∗

f given by Γ(x) = f (x) ∗ f (−x),

that is,

Γ(x)

def

f (t) f (t − x) dt for any x ∈ R.

13.5.b Pr operties

Since th e autocorrelation function is the convolution of f with the conjugate

of it s transpose Γ(x) = f (x)∗f (−x) , it is possible to use the known properties

of the Fourier t ransform to derive some interesting properties. In particular,

THEOREM 13.28 The Fourier transform of the autocorrelation function of f is equal

to the spectral density of f :



Γ(t)



= F



f (x) ∗ f (−x)





f (ν)



Autocorrelation of a ﬁnite energy function 369

PROPOSITION 13.29 The a utocorrelation function of any ﬁnite energy func tion f

is hermitian: Γ(−x) = Γ(x) for all x ∈ R.

Moreover, if f is real-valued, then Γ is an ev en, real-valued function.

In addition, since



2πiν x



¶ 1, we have the inequality



Γ(x)



f (ν)



2πiν x

dν



f (ν)



dν = Γ(0),

from which we deduce:

THEOREM 13.30 The modulus of the autocorrelation function of a function f is

maximal at the origin: |Γ(x)| ¶ Γ(0) for any x ∈ R. Γ(0) is real, positive, and

equal to the energy of f : Γ(0) =

|f |

DEFINITION 13.31 The reduced autocorrelation function, also called the

self-coherence function of f , is given by

γ(x)

def

Γ(x)

Γ(0)

This function γ(x) is thus always of modulus between 0 and 1.

13.5.c Intercorrelation

DEFINITION 13.32 The intercorrelation function of two square integrable

functions f and g is th e function

f g

(x)

def

f (t) g(x − t) dt.

From the Cauchy-Schwarz inequality, we derive



f g

(x)



¶ Γ

(0) Γ

(0).

This brings us to t he deﬁnit ion of the coherence function:

DEFINITION 13.33 The intercoherence function, or coherence function,

of f and g is the reduced intercorrelation function

f g

(x)

def

f g

(x)

(0) Γ

(0)

The modulus of this coherence function is therefore also always between 0

and 1.

370 Physical applications of the Fourier transform

13.6

Finite power functions

13.6.a Deﬁnitions

Up to now, the functions which have been considered are mostly square inte-

grable, that is, functions in L

(R). In many physical situations (in optics, for

instance), the integral

|f |

represents an energy. Sometimes, however, th e

objects of interest are not functions with ﬁnite energy but those with ﬁnite

power, such as f (t) = cos ωt.

DEFINITION 13.34 A function f : R → C is a ﬁnite power f unction if the

limit

lim

T →+∞

−T



f (t)



exists and is ﬁnite. This limit is then the average power carried by the

signal f .

The spectral density may also be redeﬁned:

DEFINITION 13.35 Let f be a ﬁnite power signal. The spectral density, or

power spectrum, of f is t he function deﬁned by

W (ν)

def

= lim

T →+∞



−T

f (t) e

−2πiνt



An analogue of the Parseval formula holds for a ﬁnite power signal:

THEOREM 13.36 Let f (t) be a ﬁnite power signal and W (ν) its spectral density.

Then we have

lim

T →+∞

−T



f (t)



dt =

+∞

−∞

W (ν) dν.

13.6.b Autocorrelation

For a ﬁnite power f unction, the previous deﬁ nit ion 13.27 of the autocorrela-

tion is not valid anymore, and is replaced by the following:

DEFINITION 13.37 The autocorrelation function of a ﬁnite power signal f

is given by

Γ(x)

def

= lim

T →+∞

−T

f (t) f (t − x) dt.

The Wiener-Khintchine theorem 371

S(t)

(S)

(t)

Fig. 13.1 — Light interference e xperiment with Young slits.

The analogue of Theorem 13.28 is

THEOREM 13.38 The Fourier transform of the autocorrelation function of a ﬁnite

power signal is equal to the spectral density:



Γ(t)



= W (ν).

Example 13.39 Let f (t) = e

2πiν

. The autocorrelation f u nction is Γ(x) = e

2πiν

and the

spectral density is W (ν) = δ(ν − ν

). Using the deﬁnition for a ﬁnite energy function, we

would have found instead that

f (ν) = δ(ν − ν

) and the spectral density would have to be

something like δ

(ν −ν

). But, as explained in Chapter 7, the square of a Dirac distribution

does not make sense.

13.7

Application to optics:

the Wiener-Khintchine theorem

We consider an optical interference experiment with Young slits which are

lighted by a point-like light source (see Figure 13.1).

We will show that, in the case wh ere the source is not quite monochromatic

but has a certain spectral width ∆ν, the interference ﬁgure will get blurry at

points of the screen corresponding to differences in the optical pat h between

the two light rays which are too large. The threshold difference between

the optical paths such that the diffraction rays remain visible is called the

coherence length, and we will show that it is given by ℓ = c/∆ν.

Consider a “nonmonochromatic” source. We a ssume that the source S

of th e ﬁgure emits a real signal t 7→ S

(R)

(t), and t hat an analytic complex

signal t 7→ S (t) is associated with it. Hence, we have S

(R)

(t) = Re



S(t)



. Th e

Fourier transform of S

(R)

(t) is denoted S

(R)

(ν).

Moreover, we assume that t he signal emitted has ﬁnite power a nd is char-

acterized by a spectral power d ens ity W (ν) for ν > 0. The signal is non-

372 Physical applications of the Fourier transfor m

monochromatic if the spectral density W (ν) is not a Dirac distribution.

In the proposed experiment, we look for the light intensity a rriving a t the

point P , given by t he time average of the square of the signal S

(t) arriving

at the point P :





(t)





where we put





(t)





def

= lim

T →+∞

−T



(t)



dt.

The signal reaching P is the s um of the two signals coming from the two slits.

The signal coming from one slit is thus the same as the signal coming from

the other, but with a time shift τ = ∆L/c, where ∆L is the path difference

between the two rays (and hence depends on the point P ):

(t) = S

(t) + S

(t) = S

(t) + S

(t −τ).

(The function S

(t) is directly related to the signal S (t) emitted by the source.)

From this we derive

· S

+ S

) ·(S

+ S

)

· S

+ 2Re

· S

= 2I + 2Re

· S

denoting by I the average value

· S

, which is the light intensity of

the signal that passes by a single slit without interference. All information

concerning the inter ference phenomenon is given by the term 2Re

· S

which is easy to compute:

· S

(t) · S

(t −τ)

= Γ(τ),

where Γ(τ) is the autocorrelation f unction of t he complex signal S

, also

called here the autocoherence function.

(Recall that τ is a function of the

observation point P .)

So ﬁnally the light intensity at the point P is given by

= 2I + 2 Re



Γ(τ)



= 2I

1 + Re



γ(τ)



with

γ(τ)

def

Γ(τ)

Γ(0)

Γ(τ)

In some optics books, the normalized autocorrelation function γ(τ) = Γ(τ)/Γ(0) is also

called the autocoherence function.

The Wiener-Khintchine theorem 373

Γ(0)

min

max

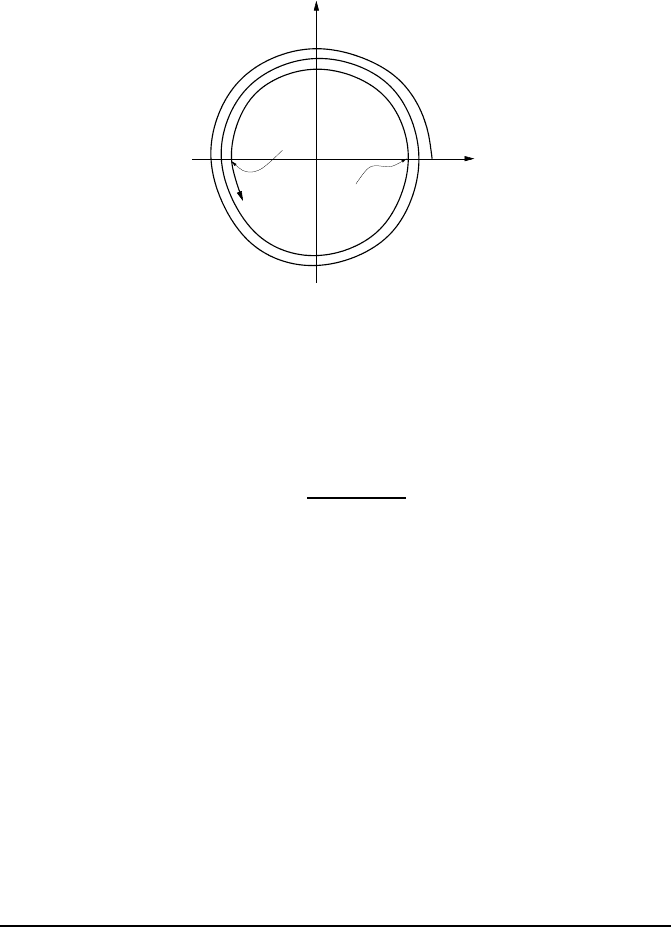
Fig. 13.2 — The autocorrelation function for an almost monochromatic source, varying

with the p arameter τ in the complex plane. The value at the origin Γ(0) is

real and positive. The modulus of Γ(t) varies slowly compared to its phase.

We may th en estimate the visibility factor of t he diffraction ﬁ gure, using

the Rayleigh criterion [14]:

V =

max

− I

min

max

+ I

min

. (13.2)

Here, I

max

represents a local maximum of the light intensity, not at the point P ,

but in a close neighborhood of P ; that is, the obs ervation point will be moved

slightly and hence the value of the parameter τ will change until an intensity

which is a local maximum is found, which is denoted I

max

. Similarly, the

local minimum in the vicinity of P is found and is denoted I

min

Estimating this parameter is only possible if the values τ

max

and τ

min

corresponding to the maximal and minimal intensities close to a given point

are such that the difference τ

max

−τ

min

is very small compared to the duration

of a wave train. If this is the case, the autocorrelation function will have

the shape in Figure 13.2, that is, its phase will vary very fast compared to its

modulus; in particular, the modulus of Γ will remain almost constant between

max

and τ

min

, whereas the phase will change by an amount equal to π.

For

τ = 0, we have of course Γ = I, and then |Γ(τ)| will decrease with time.

Thus, by moving slightly P , τ varies little and |Γ| remains essentially

constant. Then Re(Γ) varies between −|Γ| and + |Γ|, and the vis ibility factor

This is what the physics says, not the mathematics! This phenomenon may be easily understood.

Suppose τ is made to vary so that it remains small during the duration of a wave train. Then,

taking a value of τ equal to half a period of the signal (which is almost monochromatic), the

signals S

and S

are simply shifted by π: they are in opposition and Γ(τ) is real, negative,

and wi th absolute value almost equal to Γ(0). If we take values of τ much larger, the signals

become more and more decorrelated because it may be that S

comes from one wave train

whereas S

comes from another. A simple statistical model of a wave train gives an exponential

decay of



Γ(τ)



374 Physical applications of the Fourier transfor m

for the rays is then simply

V (τ) = |γ(τ)| =



Γ(τ)



But, according to Theorem 13.38, the autocorrelation function is given by the

inverse Fourier transform of the power spectrum:

Γ(τ) =

+∞

W (ν) e

2πiντ

dν.

The following theorem follows:

THEOREM 13.40 (Wiener-Khintchine) The visibility factor of the dif fraction ﬁgure

in the Young inter ference experiment is equal to the modulus of the normalized Fourier

transform of the spectral density of the source evaluated for the value τ corresponding to

the time difference between the two rays:

V =



+∞

W (ν) e

2πiντ

dν

+∞

W (ν) dν



So, take the case of an a lmost monochromatic source — for instance, a

spectral lamp, which should emit a monochromatic light but , because of the

phenomenon of emiss ion of light by wave trains, is characterized by a nonzero

spectral wid th. If we denote by ∆ν the spectral widt h, we know that the

Fourier transform of the spectral energy densit y has typical width ∆t = 1/∆ν;

for a time difference τ ≫ 1/∆ν, that is , for a path difference ≫ c/∆ν,

the diffraction pattern will become blurred. The quantity ∆t = 1/∆ν is the

coherence time and the length ℓ = c/∆ν is the cohe rence length.

Remark 13.41 A similar theorem, due to P. K. van Cittert and Frederik Zernike (winner

of the Nobel pri ze in 1953), links the visibility factor of a diffraction ﬁgure to the Fourier

transform of t h e spacial distribution of a monochromatic extended source. The interested

reader may consult [14] or look at Exercise 13.2.

Exercises 375

EXERCISES

 Exercise 13.1 (Electromagnetic ﬁeld in Coulom b gauge) We consider an elec tromagnetic

ﬁeld



E( r , t), B( r, t)



compatible with a ch arge and current distribution



ρ( r, t), j( r, t)



that is, such that the ﬁelds satisfy the differential equations (Maxwell equations):

div E = −ρ/ǫ

, curl E = −

∂ B

∂ t

div B = 0, curl B =

∂ E

∂ t

+ µ

i) Show that the ﬁeld B is transverse.

ii) Show that the longitudinal component of the electric ﬁeld is given by the instantaneous

Coulomb potential associated with the charge distribution. What may be said from the

point o f view of relativity theory?

iii) Is the separation between transverse and longitudinal components preserved by a

Lorentz transformation?

 Exercise 13.2 (van Cittert-Zernike theorem) Consider a light source which is translation in-

variant along the O y-axis, ch aracterized by a light intensity I(x) on the O x-axis, such that the

light passes through an interferential apparatus as described below. The distance between the

source and the slits is f and the distance to the screen is D.

x y

f D

We assume that the source may be modeled by a set a point-like sources, emitting wave

trains independently of each other, with the same frequency ν. Since the sources are not

coherent with respect to each other, we admit that the intensity observed at a point of the

interference ﬁgure is the sum of intensities coming from each source.

Show:

THEOREM 13.42 (van Cittert-Zernike) The visibility factor of the source I(x) is equal to the modulus

of the Fourier transform of the normalized spatial int ensity of the source for the spatial frequency k =

a/λ f , where a is the distance between the interference slits and f is the distance between the source and

the system:

|γ| =





λ f





with I (x)

def

I(x)

+∞

−∞

I(s) ds

The reader will ﬁnd in [14] a generalization of this result, due to van Cittert (1934) and

Zernike (1938).

We saw in Exercise 1.3 on page 43 that it is in fact necessary to have a nonzero spectral

width before the sources can be c o nsidered incoherent.

376 Physical applications of the Fourier tran sfor m

SOLUTIONS

 Solution of exercise 13.1. Applying the Fourier transform, the Maxwell equations become

k ·EE

EE = i eρ/ǫ

, i k ∧EE

EE =

∂BB

∂ t

k ·BB

BB = 0, i k ∧BB

BB =

∂EE

∂ t

+ µ

The third of the se shows that B is transverse.

Moreover, since k ·EE

EE = k ·EE

( k) = −i eρ( k)/ǫ

, we ﬁnd that

( k) =

k ·EE

EE ( k)

= i

eρ( k)/ǫ

and hence, taking the inverse Fourier transform, we have

( r , t) =

4πǫ

ρ( r

′

) [ r − r

′

]

kr − r

′

= E

Coulomb

( r , t).

Thus, t h e longitudinal ﬁeld propagates instantaneously through space, which contradicts spe-

cial relativity. This indicates that the decomposition in transverse and longitudinal components

is not physical.

In fact, it is not preserved by a Lorentz transformation, since the Coulomb ﬁeld is not.

 Solution of exercise 13.2. The intensity at a point P with coordinate y on the screen i s

given by t h e integral of intensities produced by I(x), for x ∈ R. An elementary interference

computation shows that, for small angles, we have

J (x) = K ·

+∞

−∞

I(x)



1 + cos

2πa





= K I



1 +

+∞

−∞

I (x) cos

2πa







with I

+∞

−∞

I(s) ds, and where I (x) = I(x)/I

is the normalized intensity. Since I and I

are real-valued functions, we may write

J ( y) = K I



1 + Re

+∞

−∞

I (x) exp



−

2πia







= K I



1 + Re





λ f



−2πia y/λD



If we decompose

I (a/λ f ) = |γ|e

iα

in terms of a phase and modulus, we obtain

J ( y) = K I

1 + |γ|cos



2πa y

λD

−α

ª

Now, if we observe the interference ﬁgure close to the ce nter and vary y slowly, the intensity

J on the screen varies between K I



1 − |γ|



and K I



1 + |γ|



, which shows that |γ| i s the

visibility factor of the interference ﬁgure, which is what was to be shown.

This result is useful in parti cular to measure the angular distance between two stars, or the

apparent diameter of a star, using two telescopes set up as interferometers.