Антонова Н.Б., Вечер А.В. Прогнозирование и планирование экономики

Подождите немного. Документ загружается.

В процессе анализа применяются и другие приемы и

методыW– прямого счета, опроса, наблюдений и т.д. Из них

важными в совершенствовании экономического анализа,

повышении его эффективности являются экономико-

математические методы. Они существенно сокращают сроки

проведения анализа, обеспечивают более полный охват влияния

факторов на результаты экономического развития, заменяют

приближенные и упрощенные расчеты точными вычислениями,

позволяют решать новые многомерные задачи анализа, которые

практически невыполнимы традиционными методами, и

повышают научный уровень исследований в целом.

Анализ объекта (процесса, явления) присутствует на всех

стадиях планирования, прогнозирования и регулирования

экономики. Анализ неразрывно связан с синтезом, они

составляют единое методологическое целое. Анализ является

началом изучения объекта, затем следует синтез. Если в

процессе анализа объект разделяется на составляющие его

элементы, то синтез объединяет их в единое целое. При этом

синтез нельзя рассматривать как простое суммирование

элементов. Синтез позволяет по-новому представить объект –

как взаимодействие элементов, образующих единое целое.

Анализ и синтез широко применяются при планировании и

прогнозировании, при решении проблем социально-

экономического развития государства.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение методологии планирования и

прогнозирования и назовите ее основные элементы.

2. Что следует понимать под методологическими подходами и

принципами планирования и прогнозирования?

3. Назовите основные методологические принципы

планирования и дайте им характеристику.

4. Перечислите и раскройте содержание основополагающих

принципов прогнозирования.

5. Что представляет собой метод планирования и

прогнозирования, методика?

6. Что представляют собой и какую роль играют в

планировании и прогнозировании показатели?

7. Чем показатель отличается от критерия?

8. Сгруппируйте показатели в зависимости от их содержания и

направления использования и охарактеризуйте каждую из

выделенных групп.

9. Что такое логика планирования и прогнозирования, каковы

ее идея и основные составляющие?

10. Что понимается под информационной базой планирования и

прогнозирования?

11. Что представляет собой и каким требованиям должна

отвечать экономическая информация?

12. Что отличает социальную информацию от экономической?

13. Какую роль в планировании и прогнозировании выполняют

анализ и синтез?

14. Покажите цели и дайте принципиальную схему проведения

экономического анализа.

15. Что представляют собой функциональный, объектный и

объектно-функциональный подходы к анализу социально-

экономических процессов?

ТЕМА 3. ЭКСПЕРТНЫЕ (ИНТУИТИВНЫЕ) МЕТОДЫ

ПРОГНОЗИРОВАНИЯ

ЛЕКЦИЯ 3

Основные понятия:

эксперт; отбор экспертов; контрольные вопросы;

количественные оценки; качественные оценки; медиана;

квартиль; согласованность; ранг; стандартизация рангов;

метод анкетирования; метод интервью; метод комиссии;

метод дельфи; эффект первого слова; метод сценариев;

ожидаемое значение; прямой и обратный способы;

оптимистический и пессимистический варианты; ожидаемое

значение.

Области применения и общая схема работ по разработке

экспертного прогноза

В основе всех разновидностей экспертных методов

прогнозирования лежит использование знаний экспертов об

объекте прогнозирования и их способность верно предсказывать

его будущее состояние. В переводе с латинского языка эксперт –

знающий, сведущий.

Наиболее целесообразно применение интуитивных методов

прогнозирования в следующих случаях:

отсутствие достаточного объема достоверной информации

об объекте прогнозирования – т.е. нет информации об

аналогичных объектах прогнозирования или о состоянии

самого объекта прогнозирования в прошлом;

большая неопределенность состояния среды, в которой

будет происходить функционирование объекта

прогнозирования в прогнозируемом периоде (внешней

среды);

большой временной горизонт прогнозирования, т.е.

прогнозирование на большой срок, в этом случае

фактически имеем комбинацию двух предыдущих случаев

– нет достоверной информации и о самом объекте

прогнозирования и о его внешней среде.

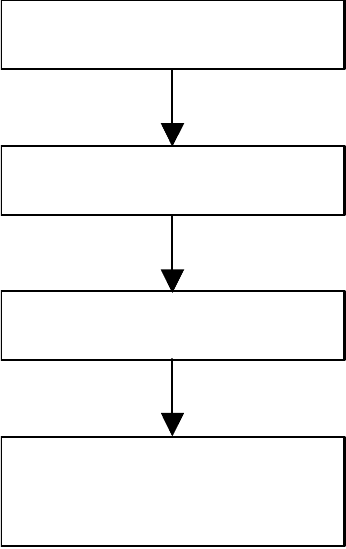
Для осуществления прогнозирования с помощью

экспертных методов в самом общем случае необходимо

выполнить целый ряд последовательных действий, общая схема

которых представлена на рис.3.

. Поиск экспертов

2. Отбор экспертов

3. Опрос экспертов

4. Обработка резуль-

татов

Рис. 3. Схема работ по разработке прогноза экспертными

методами.

Поиск и отбор экспертов

Состав экспертов участвующих в прогнозировании – это

ключевой параметр определяющий качество будущего прогноза,

по этому подбору экспертов необходимо уделить самое

пристальное внимание.

Выявить первоначальный круг лиц являющихся

потенциальными кандидатами в эксперты можно по

публикациям, так как авторы, пишущие об объекте

прогнозирования, как правило, не только хорошо знакомы с

самим объектом, но и зачастую являются наиболее

компетентными людьми по данному вопросу. Вторым способом

выявления кандидатов в эксперты является опрос о

потенциальных кандидатах среди специалистов хотя бы

отдаленно знакомых с объектом прогнозирования. Если список

кандидатов, полученный на этом шаге, не удовлетворяет

организаторов опроса, то для его последующего расширения

необходимо задать вопрос о наиболее подходящих кандидатурах

всем отобранным на предыдущем этапе. Если важность прогноза

достаточно велика, то этот вопрос необходимо задавать всем

вновь названным кандидатам. Процесс отбора кандидатов можно

считать полностью завершенным, после того как вновь

названные кандидаты называют фамилии в основном уже

имеющиеся в нашем списке.

После завершения формирования списка кандидатов из

него необходимо произвести отбор экспертов. Наиболее

простым методом отбора является выбор тех кандидатов, чьи

фамилии наиболее часто назывались на этапе поиска кандидатов

в эксперты.

Вторым методом может служить процедура самооценки

или, что значительно лучше, оценки каждым кандидатом всех

остальных кандидатов. При оценке экспертами друг друга

результаты оценки получаются значительно более

объективными, чем при самооценке, но в этом случае кандидаты

должны хорошо знать друг друга. Если это условие не

выполняется, то применяется процедура самооценки. При этом

участвующим в оценке или самооценке необходимо предложить

критерии, по которым будут оцениваться кандидаты и

обязательно указать шкалу, по которой должна производиться

оценка. В качестве критериев могут служить степень

осведомленности эксперта с теоретическими вопросами,

касающимися объекта прогнозирования, опытом практической

работы в этой области, степенью развитости интуиции по

предсказанию поведения объекта прогнозирования, глубиной

знакомства с литературными источниками. Для получения

итоговой оценки каждому из критериев необходимо присвоить

нормализованный вес. Веса считаются нормализованными, если

их сумма равна единице. О конкретных значениях весов для

каждого критерия можно задать вопрос всем участвующим в

оценке или самооценке. Сумма произведений полученных по

всем критериям оценок для каждого эксперта на веса этих

критериев представляет собой итоговую оценку эксперта.

И, наконец, последним методом отбора экспертов из списка

кандидатов может служить метод контрольных вопросов. В

этом случае кандидатам задаются вопросы об объекте

прогнозирования, ответы на которые не известны кандидатам, но

точно известны организаторам прогноза. Обычно это вопросы о

не очень важных, частных характеристиках объекта

прогнозирования в прошлом, которые в виду их

незначительности не запоминаются большинством специалистов

но организаторам опроса они точно известны из каких либо

документов (справочников, отчетов и т.д.). Например, при

подборе экспертов для прогнозирования численности

вооруженных сил РБ на перспективу, в качестве контрольного

вопроса может служить вопрос о числе женщин

военнослужащих в вооруженных силах 1995 году, при

прогнозировании развития мобильной связи – число телефонов в

сельской местности в таком-то году и т.д. При этом если есть

подозрение, что цифра достаточно известная, всегда существует

возможность ее дальнейшей детализации, например, задать

вопрос о числе телефонов у сельских жителей пенсионеров и

тому подобное. Лучшими экспертами являются те кандидаты,

которые дали наиболее точные ответы на контрольные вопросы.

Одной из важнейших проблем при отборе экспертов

является задача о минимально необходимом их числе. К

сожалению, ясного ответа на этот вопрос теория не дает.

Возможен ответ лишь о том достаточно ли экспертов, но этот

ответ можно получить только после обработки результатов

опроса. Минимальное число экспертов можно оценить по

формуле:

)5/3(5.0

min





где:

min

– минимально необходимое число экспертов;

max









- относительное изменение среднего значения

ответов экспертов при добавлении еще одного эксперта;

– среднее значение ответов экспертов;



– среднее значение ответов экспертов при добав-

лении еще одного эксперта;

max

– максимальное значение в ответах экспертов.

Опрос экспертов

Как правило, эксперты показывают более надежные

результаты, если отвечают на заранее поставленные вопросы, по

этому при подготовке опроса их необходимо подготовить

заранее. Вопросы могут быть следующих видов:

открытые – не имеют готовых вариантов ответа;

закрытые – экспертам предлагается выбрать один из

предложенных вариантов;

косвенные – вопросы применяемые в тех случаях когда

ответ эксперта может характеризовать его морально-

психологические качества и существует опасность того, что

эксперт не будет при ответе полностью искренним, т.е. может

исказить ответ по этическим соображениям.

По методу проведения опросы могут быть

индивидуальными или коллективными, очными или заочными.

К достоинствам индивидуального метода опроса следует

отнести его меньшую трудоемкость, так как нет необходимости

в обеспечении одновременной явки всех экспертов на заседание.

Кроме этого над мнением отдельных экспертов не довлеет

мнение большинства или наиболее авторитетных их них. Но в

тоже время эксперты при прогнозировании ориентируются

только на свое представление об объекте прогнозирования и

лишены возможности учитывать все многообразие информации,

характерное для коллектива людей.

Коллективный опрос более трудоемок в части подготовке

заседания, при коллективном обсуждении наблюдается эффект

психологического давления мнения большинства и мнения

наиболее авторитетных экспертов над мнением остальных. В

качестве основного преимущества коллективного опроса следует

отметить тот факт, что в этом случае эксперты получают

возможность осуществлять свой прогноз, базируясь не только на

собственных представлениях об объекте прогнозирования, но и

использовать большее разнообразие информации об объекте

прогнозирования, почерпнутое в процессе коллективного

обсуждения. Правда при этом эксперты, стремясь сохранить

высокую оценку своей компетентности как специалиста,

склонны отстаивать ранее публично высказанную точку зрения,

а значит, психологически менее склонны воспринимать другие,

отличные от своей точки зрения, после того как публично

высказали свою.

Заочные опросы менее трудоемки, чем очные, но в них

всегда существует опасность того, что эксперт не верно

понимает вопрос, а у проводящего опрос нет возможности это

выявить.

Для очных опросов все характерно с точностью до

наоборот: они более трудоемки, но меньше опасность получить

ответы на неверно понятые вопросы, так как в этом случае

проводящие опрос присутствуют при обсуждении ответов, а

значит имеют возможность оценить насколько верно поняты

вопросы экспертами.

Обработка количественных ответов экспертов

В результатe работы экспертов обычно является целая

палитра мнений. Задача обработки полученных результатов

предполагает поиск ответа на два вопроса: первый – чему

собственно равен коллективный ответ экспертов, второй –

можно ли им доверять.

В зависимости от содержания поставленных вопросов

ответы экспертов могут быть количественными или

качественными. Количественные ответы получаются у

экспертов при оценке ими прогнозируемой величины с

использованием двух типов шкал - шкалы отношений или

интервальной шкалы.

Оценки по шкале отношений это оценки в обычных

натуральных измерителях: метрах, рублях, килограммах и т.д. В

этом случае информативна как сама величина, так и ее отличие

от другой подобной величины. Другими словами, в случае

оценки по шкале отношений можно говорить и о том, насколько

велика оцениваемая величина и о том, насколько она отличается

от другой такой же величины.

Оценки по интервальной шкале получаются в тех случаях,

когда оцениваемый параметр не удается измерить натуральным

измерителем, например чувства и эмоции людей. В этом случае

экспертов просят оценить прогнозируемую характеристику по

какой-то цифровой шкале. Абсолютная величина получаемой

оценка не имеет смысла сама по себе, но разность между двумя

такими оценками говорит о степени близости двух объектов друг

к другу по оцениваемому свойству.

В обоих вариантах количественной оценки методика

обработки результатов одна и та же. Для ответа на вопрос о

коллективном мнении экспертов традиционно используется

среднее значение. Но эта величина не является лучшим

выражением коллективного мнения экспертов, так как она может

сильно меняться при наличии сильно отличающихся мнений,

особенно в тех случаях, когда эти сильно отличающиеся мнения

не симметричны, т.е. число оптимистов не равно числу

пессимистов. Более правильно считать, что коллективное мнение

экспертов точнее оценивается медианой. Медиана это такое

значение, которое делит все ответы экспертов пополам, одна

половина ответов меньше медианы, вторая – больше.

Проиллюстрируем это утверждение на следующем примере.

Имеем оценки трех экспертов – 2, 3, 1. Медиана и средняя для

них одинаковы и равны 2. Теперь добавим мнение четвертого

эксперта, оно равно 10. В результате средняя для четырех

ответов равна 4, а медиана 2.5.

Ответ на вопрос о том можно ли доверять мнению

экспертов решается с помощью оценки степени согласованности

их мнений. В основе такого решения лежит подход, основанный

на здравом смысле: мы склонны верить утверждению других,

когда все говорят одно и тоже, и не доверять, если каждый из

них говорит что-то сильно отличающееся от ответов других.

С целью оценки степени согласованности мнения экспертов

необходимо найти первую и третью квартили. Кварта в переводе

с латинского это четверть. Первая квартиль это такое значение,

которое делит ответы экспертов в пропорции одна четвертая и

три четвертых. Одна четвертая это ответы меньшие первой

квартили, три четвертых - все ответы которые больше первой

квартили. Третья квартиль делит ответы экспертов

соответственно в пропорции три четвертых и одна четвертая.

Три четвертых это ответы, которые меньше третьей квартили, а

одна четверть – ответы которые больше. Для нахождения