Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.

D
∆ g
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
j
j
j
(I)
(II)
(III)
ω
~
ω
ω
ω
ω
ω
~
~
~
~
~
j
j
j
j
j
j
j
j
j
˜ω
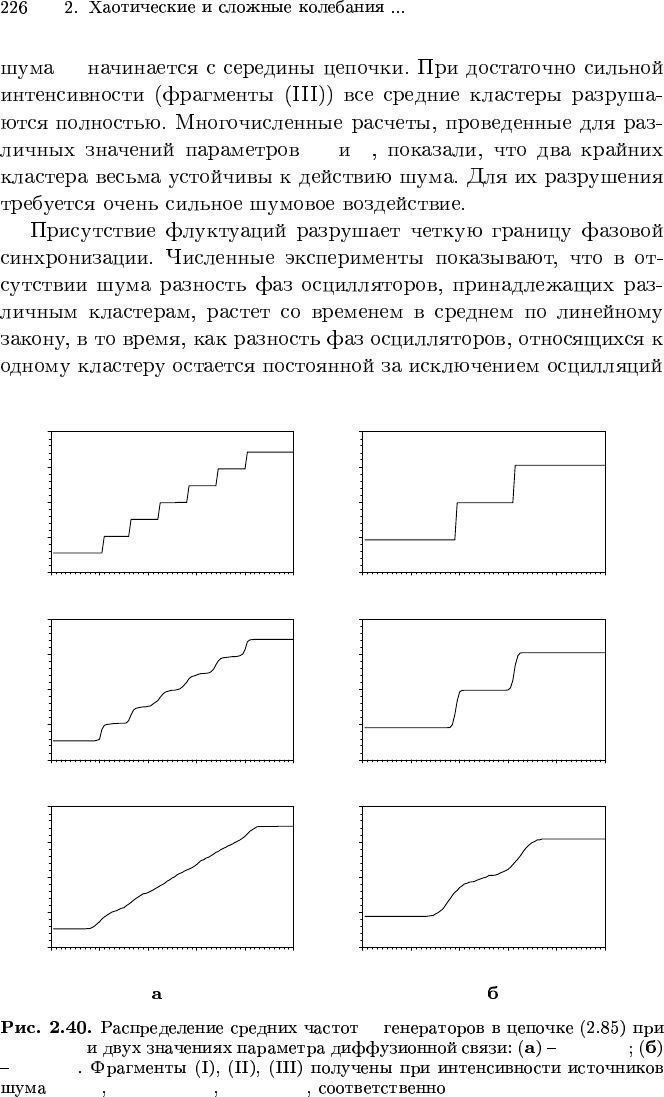
∆ = 0.002 g = 0.55
g = 3.8
D = 0 D = 0.00001 D = 0.001

[−π, π]
j
j
D
eff
θ
j (j + 1)
D
eff
(j) = lim
t→∞
1
2
D
dσ
2
θ
j
(t)
dt
E
,
σ
2
θ
j
(t) = hθ
2
j
(t)i − hθ
j
(t)i
2
.
39 ≤ j ≤
62 D
D
eff
j
j
D
max
eff
D
eff
≤ D
max
eff
D
max
eff
D
max
eff
= 0.001
D = 0.001
j = 43 j = 56
30 35 40 45 50 55 60 65 70
j
0.000
0.005
0.010
D
eff
max
D
eff
j D = 10
−8
D = 10
−5
D = 10
−3
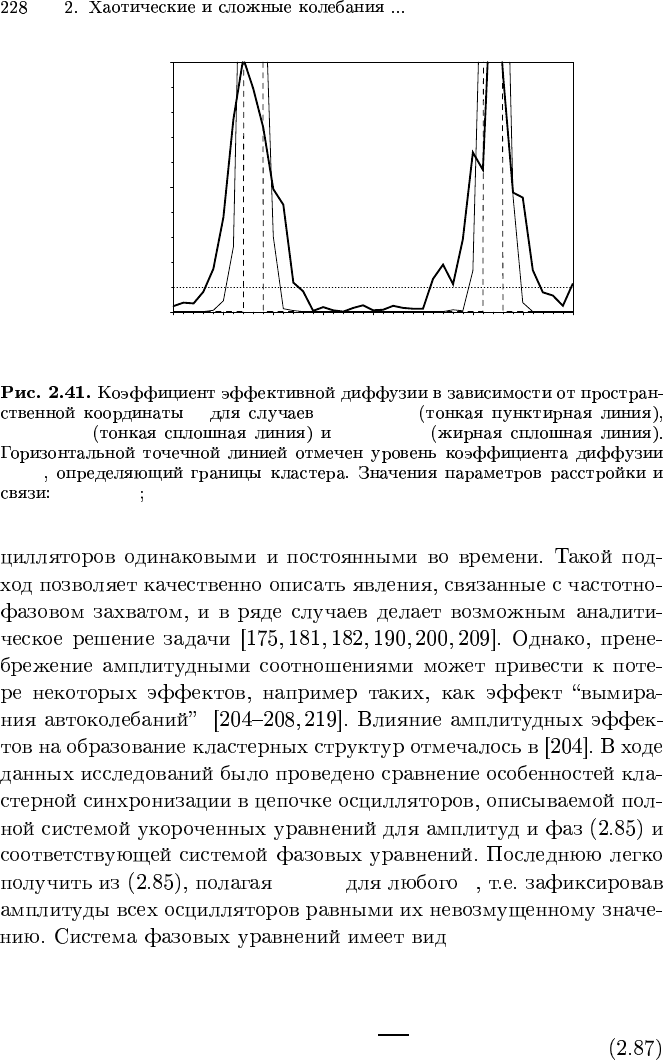
D
max
eff
∆ = 0.002 g = 3.8
ρ
j
= 1 j
˙
Φ
j
= ω
1
+ (j − 1)∆ + g(sin(Φ
j+1
− Φ
j
) −
− sin(Φ
j
− Φ
j−1
)) +
√
2Dη
j
(t),
j = 1, 2, . . . , m.
Φ
0
= Φ
1
Φ
m+1
= Φ
m
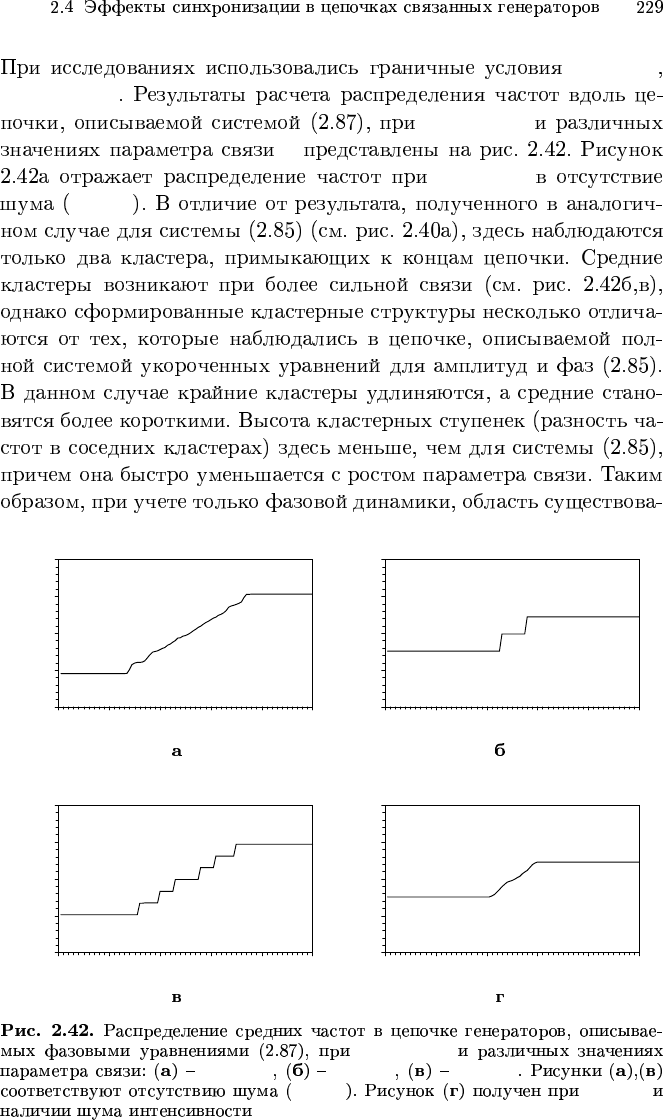
∆ = 0.002
g
g = 0.55
D = 0
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
0 20 40 60 80 100
1.00
1.05
1.10
1.15
1.20
~
ω
j
j
ω
~
j
j
ω
~
j
j
ω
j
~
j
∆ = 0.002
g = 0.55 g = 0.7 g = 1.5
D = 0 g = 1.5
D = 10
−5

D = 10
−5
˙x
1
= −ω
1
y
1
− z
1
+ C sin ω
ex
t,
˙y
1
= ω
1
x
1
+ αy
1
,
˙z
1
= β + z
1
(x
1
−µ)
˙x
j
= −ω
j
y
j
− z
j
+ γ(x
j−1
− x
j
),
˙y
j
= ω
j
x
j
+ αy
j
,
˙z
j
= β + z
j
(x
j
− µ),
j = 2, 3, . . . , m,
j
m γ
α, β, µ ω
j
C ω
ex
ω
j
= ω
1
= 0.924
α = 0.2, β = 0.2, µ = 4
ρ
j
Φ
j

x
j
= ρ
j
cos Φ
j
, y
j
= ρ
j
sin Φ
j
.
j = 1, 2, 3, . . . , m.
˜ω
j
˜ω
j
= ω
0
≈ 0.9981, j =
1, 2, . . . , m
ω
0
ω
ex
ω
0
j
lim
t→∞
|Φ
j
(t) − Φ
ex
(t)| < ∞,
Φ
ex
= ω
ex
t
j ˜ω
j
= ω
ex
W
j
= ˜ω
j
/ω
ex
(j = 1, 2, . . . , m.)
j
|W
j
− 1| ≤ ε
ε 10
−4
C ω
ex
γ = 0.01
(C, ω
ex
)
j ≥ 2
(C, ω
ex
)
S
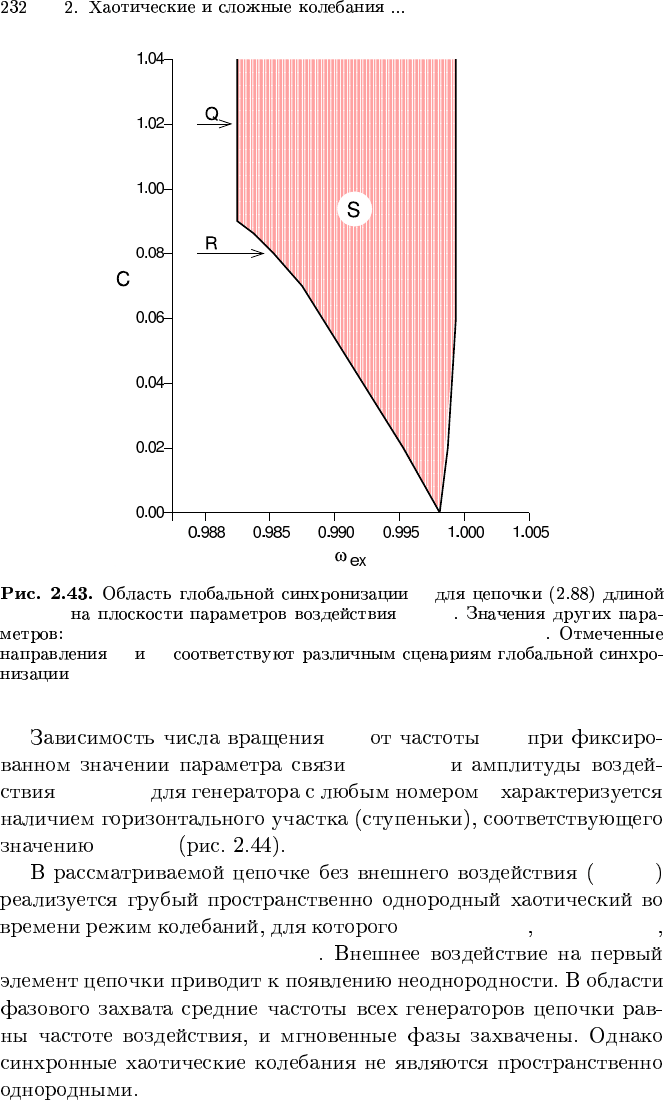
S
m = 50 ω
ex
, C
α = β = 0.2, µ = 4, ω
j
= 0.924, j = 1, 2, . . . , 50, γ = 0.01
R Q
W
j
ω
ex
γ = 0.01
C = 0.08 j
W
j
= 1
C = 0
x
j
(t) = x
k
(t) y
j
(t) = y
k
(t)
z
j
(t) = z
k
(t) (j, k = 1, 2, . . . , m)

0.98 0.99 1.00
ω
ex
0.990
0.995
1.000
1.005
1.010
W
j
j=50
j=2
W
j
ω
ex
j = 2 j = 50
γ = 0.01 C = 0.08
(x
1
, x
j
)
j
ω
ex
= 0.992
hΦ
1
(t) − Φ
j
(t)i
j
j j = 9, 11, 13
±2πk, π/2 ± 2πk, π ± 2πk, (k = 0, 1, 2, 3, . . .)
j = 42, 44, 47
ω
ex
hΦ
1
(t) − Φ
j
(t)i
ω
ex
= 1.025
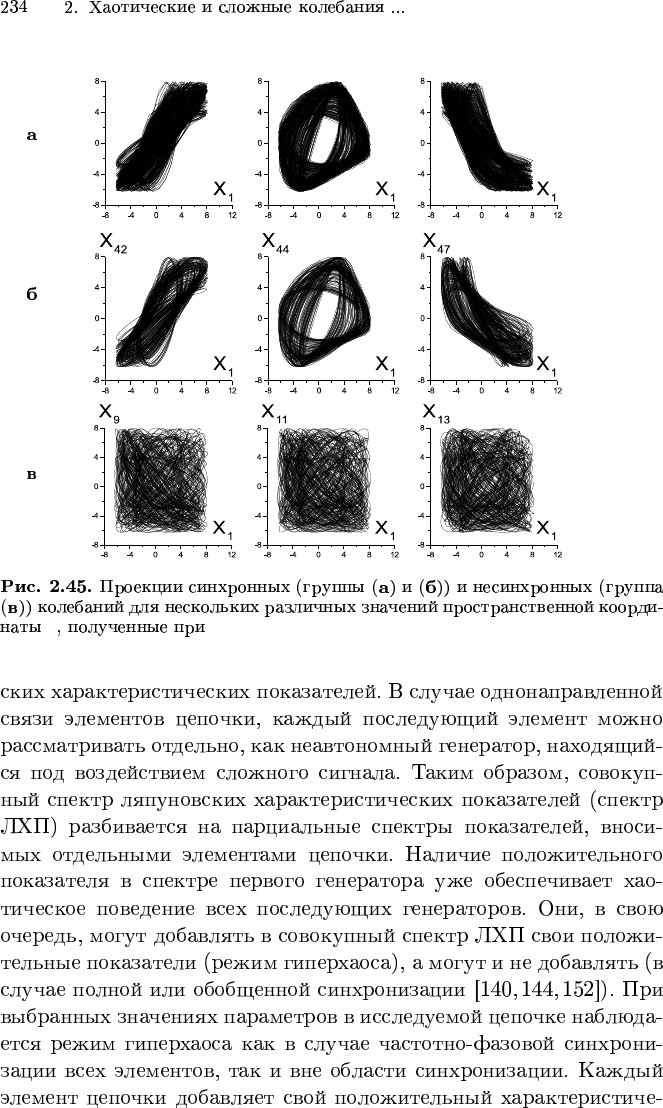
X
9
X
11
X13
j C = 0.1, γ = 0.006

m 2m
˙x
i
= α(y
i
− x
i
−f(x
i
)),
˙y
i
= x
i
− y
i
+ z
i
+ γ(y
i−1
+ y
i+1
− 2y
i
),
˙z
i
= −βy
i
,
