Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.


5

ω
0

˙x
1
= (m
1
− z
1
)x
1
+ y
1
+ γ
1
(x
2
− x
1
+ y
1
− y
2
/p),
˙y
1
= −x
1
,
˙z
1
= g
1
(f(x
1
) − z
1
),
˙x
2
/p = (m
2
− z
2
)x
2
+ y
2
+ γ
2
(Bx
1
− x
2
+ y
2
− Bpy
1
),
˙y
2
/p = −x
2
,
˙z
1
/p = g
2
(f(x
2
) − z
2
),
m
1,2
g
1,2
p = C
1
/C
2
γ
1,2
B
γ
1
= 0, B = 3
γ
1
= γ
2
, B = 1
f(x)
x
2
x ≥ 0 0 x < 0
f
1
: f
2
= 1 : 1
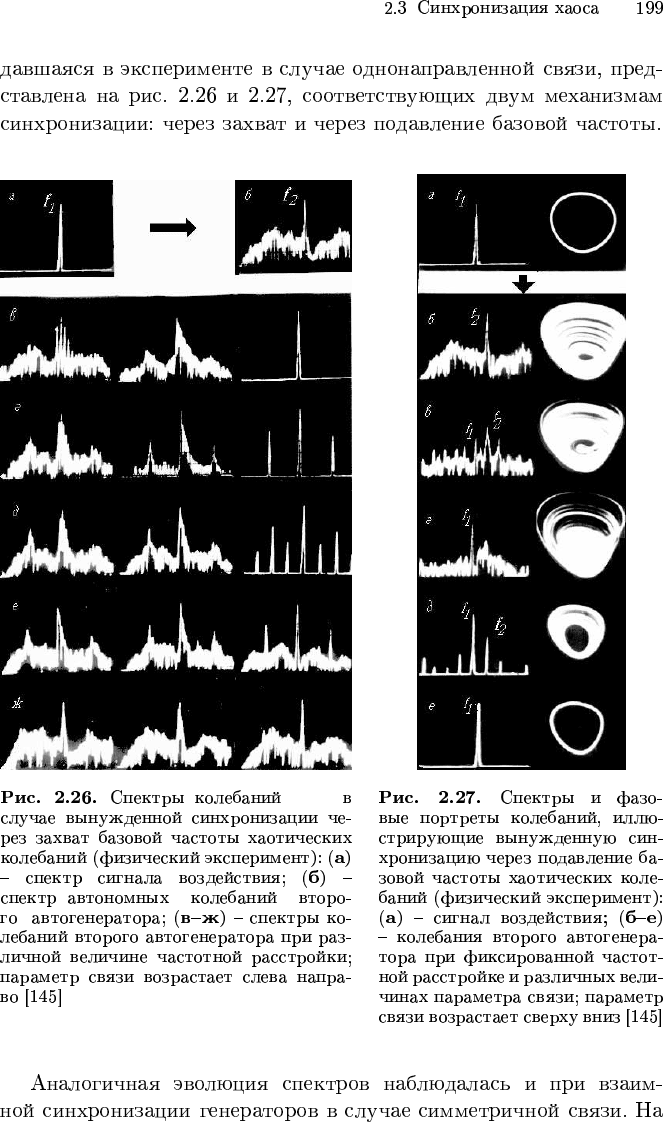
x
2
(t)

1 : 1 l
2
1
2T
0
l
k
2
, k = 1, 2, 4
kT
0
l
k
0
, k = 1, 2
ω
0
1
p < 1
ω
0
2
p > 1
kT
0
kT
0
, k = 2, 3, 4, 8, . . . kT
0
T
0
T
0
f
1
= f
2
= f
0
CA
0
CA
0
0
CA
3
CA
2

x(t) = A(t) cos (Φ(t)),
A(t) Φ(t)
Φ(t) = hΦ(t)i + δφ(t),
δφ hΦ(t)i
hω(t)i = h
dΦ(t)
dt
i = ω
av
hΦ(t)i = Φ
0
+ ω
av
t,
Φ
0
Φ(t) ω
av
ω
0
ω
av
f(t) = sin (ω
s
t + Φ
s
)
h∆Φi = hω
av
t+ Φ
0
+δφ(t) −(ω
s
t+ Φ
s
)i = (ω
av
−ω
s
)t+ Φ
0
−Φ
s
ω
av
= ω
s
Φ
0
− Φ
s
= const

˙x = −Ωy −z + γ sin ω
s
t,
˙y = Ωx + αy,
˙z = β + z(x − µ).
ω
s
Ω ω
av
ω
0
Ω Ω
D
eff
xy
Ω
1,2
ω
av
∆Φ(t) = Φ(t) − ω
s
t
µ = 6.5
Φ(t) x
y
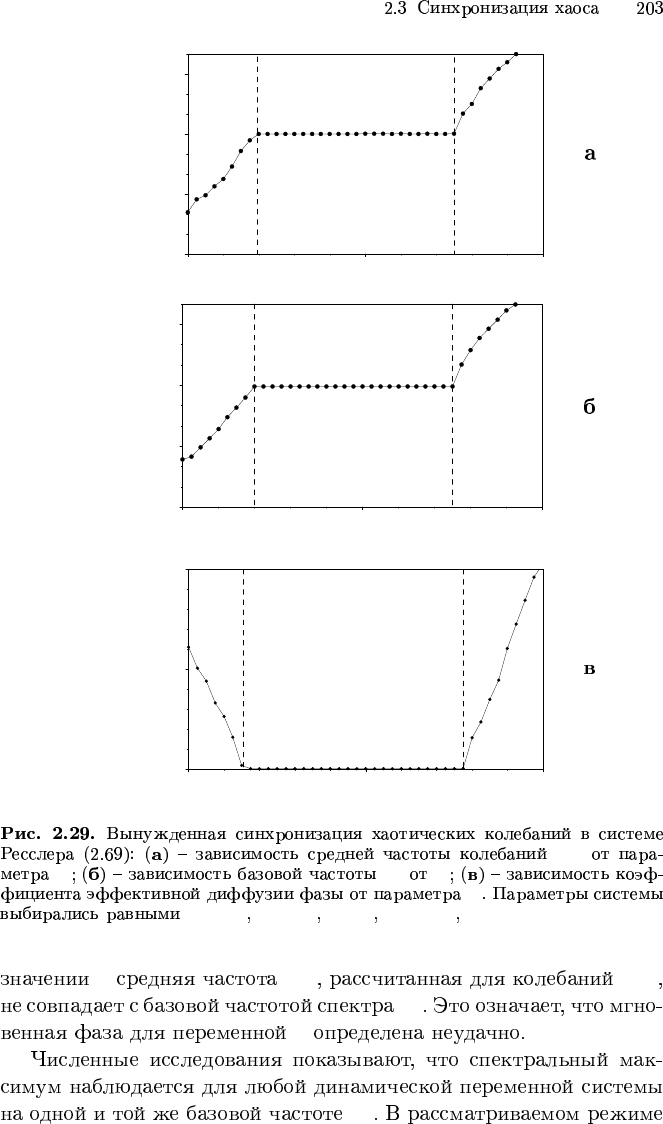
0.921 0.926 0.931
Ω
0.994
0.997
1.000
1.003
ω
av
Ω
1
Ω
2
0.921 0.926 0.931
Ω
0.994
0.997
1.000
1.003
ω
0
Ω
2
Ω
1
0.921 0.926 0.931
Ω
0.000
0.005
0.010
D
eff
Ω
2
Ω
1
ω
av
Ω ω
0
Ω
Ω
α = 0.2 β = 0.2 µ = 4 C = 0.02 ω
s
= 1
µ ω
av
y(t)
ω
0
y
ω
0

0 200 400 600 800 1000
t
−150
−100
−50
0
50
∆Φ(t)
1
2
∆Φ(t) = Φ(t) − ω
s
t
µ = 6.5 C = 0.05 Ω = 1 ω
s
= 1.068
Φ(t) x y
∆ = Ω − ω
s
6

x
1
= F (x
1
, α
1
) + γg(x
2
, x
1
),
x
2
= F (x
2
, α
2
) + γg(x
1
, x
2
),
x
1,2
∈ R
N
α
1,2
γ g
x
1
= x
2
g(x
1
, x
2
) = g(x
2
, x
1
) = 0 α
1
= α
2
U (x
1
= x
2
)
U
U
U
γ
τ
d
x
1
(t) = x
2
(t + τ
d
)
7
