Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.


Φ(t) ω
1
Ψ(t) ω
2
|mΦ(t) − nΨ (t)| = const, mf
1
= nf
2
,
m n
m = n = 1

¨x − ε(1 − x
2
) ˙x + ω
2
0
x = 0 ,
ε
ω
0
−2ω
0
< ε < 0
s
1,2
=
ε
2
± i ω
0
s
1 −
ε
2ω
0
2
.
ε > 0
0 < ε 1

T =
2 π
|Im s
1,2
|
, Im s
1,2
= ω
0
s
1 −
ε
2ω
0
2
,
ω
0
¨x − ε(1 − x
2
) ˙x + ω
2
0
x = a cos(ω
1
t + ϕ
0
),
a ω
1
x(t) = A exp (i ωt) = A (cos ωt + i sin ωt)
A ω
A ϕ = ωt
0 < ε 1 a = 0
x(t)
x(t) = A(t) cos(ω
1
t + ϕ(t)), ˙x(t) = −ω
1
A(t) sin(ω
1
t + ϕ(t)),
A(t)
ϕ(t)
A(t)
Φ(t) = ω
1
t + ϕ(t).
ϕ(t) = Φ(t) − ω
1
t
x(t)
ϕ(t)

˙ϕ(t) ω
1
A(t)
ϕ(t)
˙
A =
ε A
2
1 −
A
2
A
2
0
− µ sin ϕ,
˙ϕ = ∆ −
µ
A
cos ϕ ,
µ = a/2ω
1
∆ =
(ω
2
0
−ω
2
1
)/2ω
1
∼
=
ω
0
−ω
1
A
0
˙
A = 0, ˙ϕ = 0
˙
A = 0
˙ϕ = 0
˙
Φ = ω
1
ω
1
O
1
O
2
O
3
O
1
A = const, ϕ = const
O
1
O
2
∆
C
1

(a)
O
O
O
1
2
3
1
2
3
0
l
0
--
π π/2 ππ/2
A
φ
- -
0
0
1
2
3
1
O
3
C
A
π/2 π−π −π/2
0
1
2
3
0
φ
0
0
1
2
3
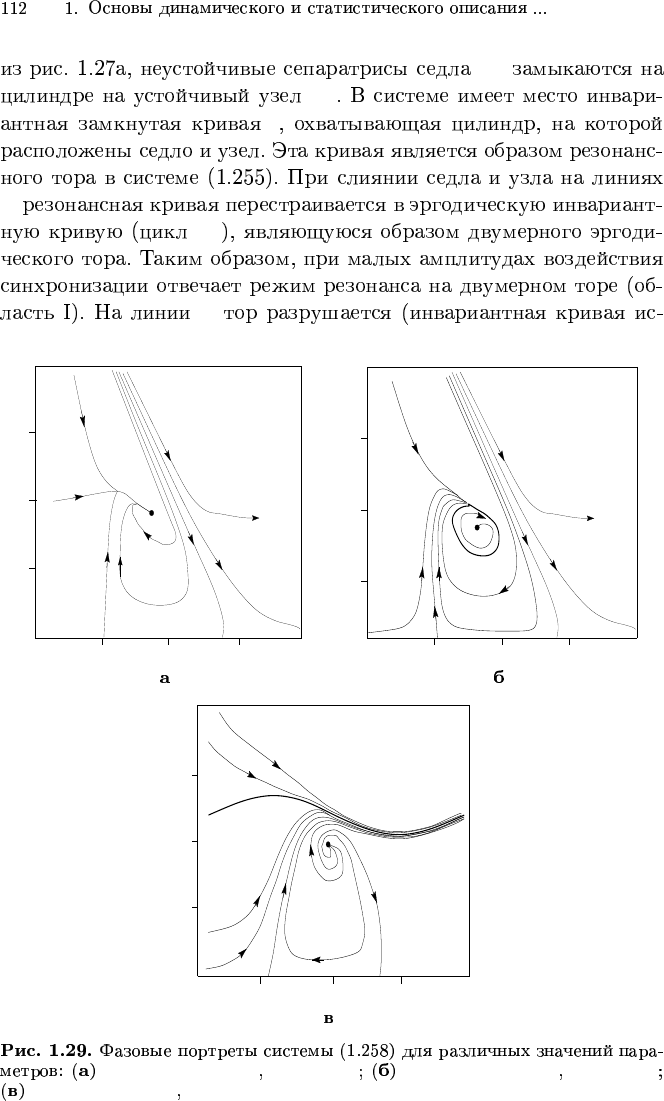
ε = 0.1, µ = 0.042, ∆ = 0.02 ε = 0.1, µ =
0.042, ∆ = 0.032
O
1
O
1
O
1
l
a
O
1
O
2
l
c
O
2
O
3
l
c
O
1
B C l
a
l
c
l
a
l
c

O
1
µ, ε
∆
∆
O
1
C
2
C
1
C
2
O
1
l
c
l
b
l
d
C
2
C
1
l
a
B, C l
b
ω
0
/ω
1
= 1
−0.16 −0.12 −0.08 −0.04 0.00 0.04 0.08 0.12
∆
0.00
0.05
0.10
0.15
0.20
µ
l
l
l
l
l
a
a
c
b
b
l
l
l
l
h
h
d
d
II
I
III
III
B
C
D
D
l
a
l
c
l
b
l
d
C
1
C
2
l
h
O
2
O
1
l
l
a
C
1
l
c
O
1
A
−π/2−π ππ/2
1
2
3
0
0
(a)
φ
0
2
1
3
0
C
2
−π −π/2 π/2 π
A
0
0
1
2
3
(b)
φ
0
1
2
3
0
A
C
1
0
1
2
3
−π π−π/2 π/20
(c)
φ
0
0
1
2
3
ε = 0.1, µ = 0.056 ∆ = 0.028 ε = 0.1, µ = 0.056 ∆ = 0.031
ε = 0.1, µ = 0.056 ∆ = 0.033

O
1
D
l
a
l
b
D
l
b
A(t)
A = const
ω
1
∆ = 0 ∆
l
h
µ ≤ 0.05
D
D l
h
l
b
µ
ω
1
= ω
0
+ ∆

ω(t) =
d
dt
Φ(t).
µ/(A
0
ε) 1 ε a/(2ω
1
A
0
)
ϕ = const
A(t) = A
0
d
dt
ϕ = ∆ −
µ
A
0
cos ϕ .
˙ϕ = −dU(ϕ)/dϕ U(ϕ) = −∆ · ϕ +
µ
A
0
sin ϕ
ϕ
U(ϕ) ∆
µ/A
0
∆ < µ/A
0
ϕ
k
= arccos (∆ ·A
0
/µ) + 2πk k = 0, ±1, ±2, . . .
hωi = lim
T →∞
1/T
R
T
0
ω(t)dt
2π
4π
−2π
−4π
0
φ
U ( )
φ
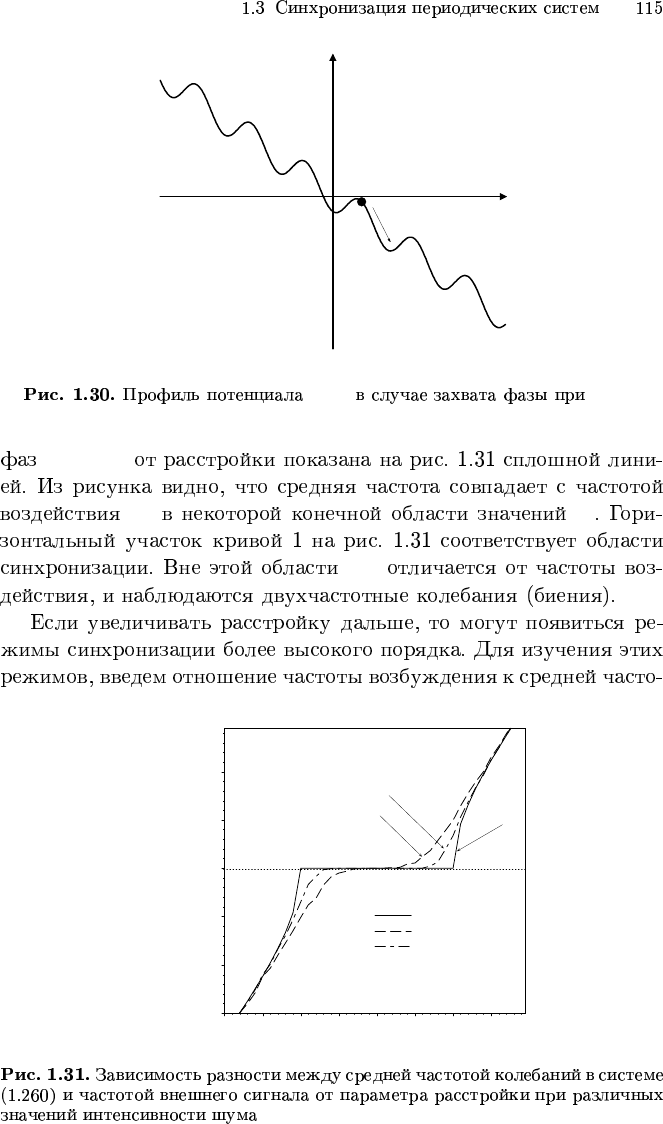
U(ϕ) ∆ 6= 0
hωi − ω
1
ω
1
∆
hωi
−0.4 −0.3 −0.2 −0.1 0.0 0.1 0.2 0.3
∆
−0.3
−0.2
−0.1
0.0
0.1
0.2
<ω>−ω
1
D=0.0
D=0.07
D=0.02
1
2
3
D
