Алєксєєва І.В., Гайдей В.О., Диховичний О.О., Федорова Л.Б. Елементарна математика. Практикум
Подождите немного. Документ загружается.

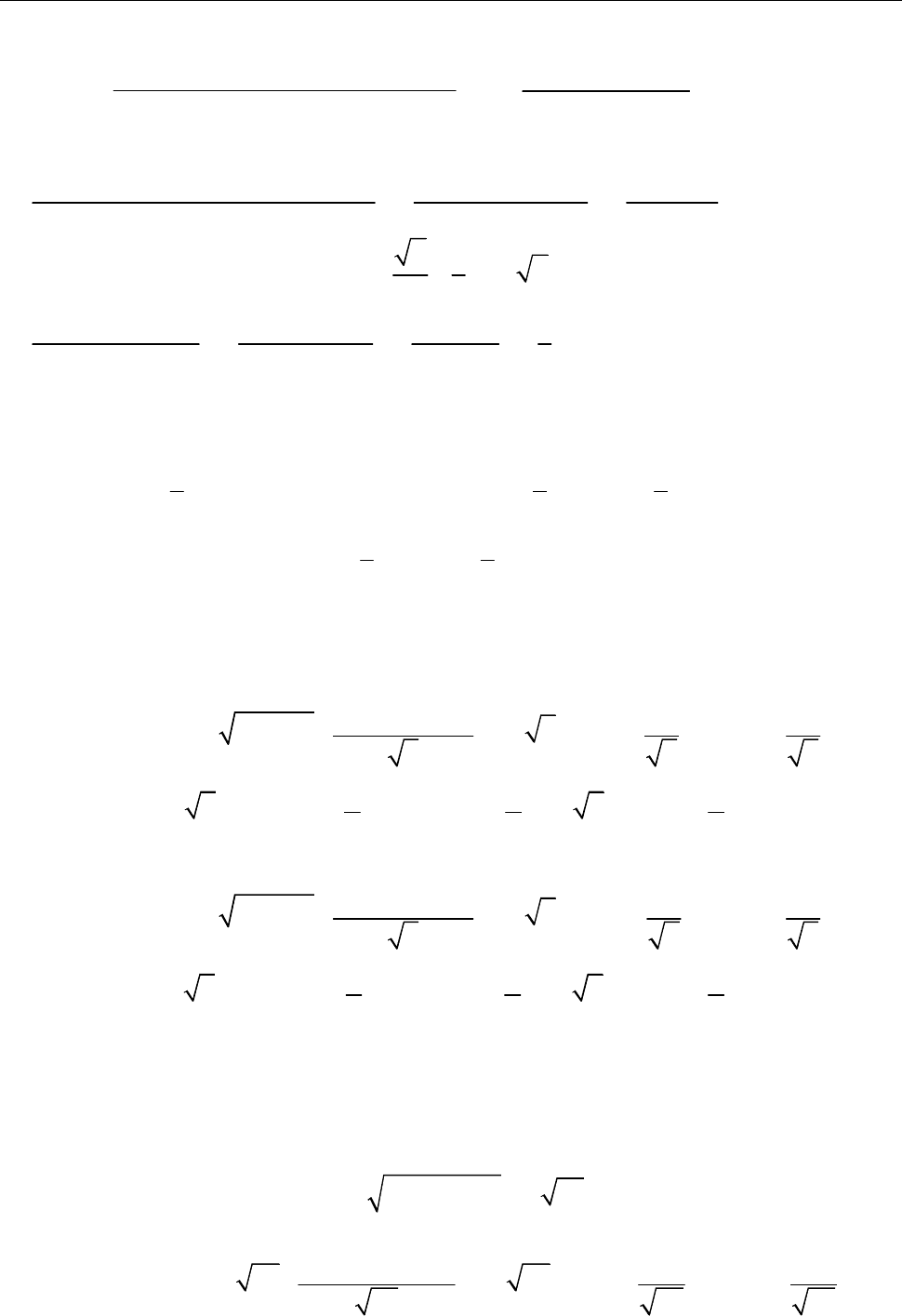
7. Тригонометричні функції. Ч. 1 71
7.5. Спростити вираз:
1)
sin 32 cos 28 cos 32 sin 28
;
sin 15 cos 15
2)
2 2
cos sin
.
cos sin
Розв’язання.
[2.3.2, 2.3.3.]
1.
[2.2.5]
sin 32 cos 28 cos 32 sin 28 2 sin(32 28 ) 2 sin 60
sin 15 cos 15 2 sin 15 cos 15 sin 30
3 1
2 : 2 3.
2 2
2.
2 2
cos sin 2 cos sin sin 2 1
tg 2 .
2 cos 2 2 cos 2 2
cos sin
7.6. Подати
cos cos 3
x x
як суму тригонометричних функцій.
Розв’язання.
[2.3.6.]
1 1 1
cos cos 3 (cos( 3 ) cos( 3 )) cos 4 cos( 2 )
2 2 2
x x x x x x x x
1 1
cos 4 cos 2 .
2 2
x x
7.7.1. Перетворити вираз
sin cos ,
x x
упроваджуючи допоміжний кут.
Розв’язання.
[2.11.2.]
І спосіб (перетворення у синус суми).
2 2
sin cos 1 1
sin cos 1 1 2 sin cos
2 2 2
x x
x x x x
2 sin cos cos sin 2 sin .
4 4 4
x x x
ІІ спосіб (перетворення у косинус різниці).
2 2
sin cos 1 1
sin cos 1 1 2 cos sin
2 2 2
x x
x x x x
2 cos cos sin sin 2 cos .
4 4 4
x x x
7.7.2. Перетворити вираз
sin 3 cos ,
x x
у синус різниці, впроваджуючи до-
поміжний кут.
Розв’язання.
[2.11.2, 2.3.2.]
[Крок 1. Визначаємо амплітуду.]
2 2
1 ( 3) 10.
A
[Крок 2. Множимо і ділимо вираз на амплітуду, перетворюємо його.]
sin 3 cos 1 3
sin 3 cos 10 10 sin cos .
10 10 10
x x
x x x x
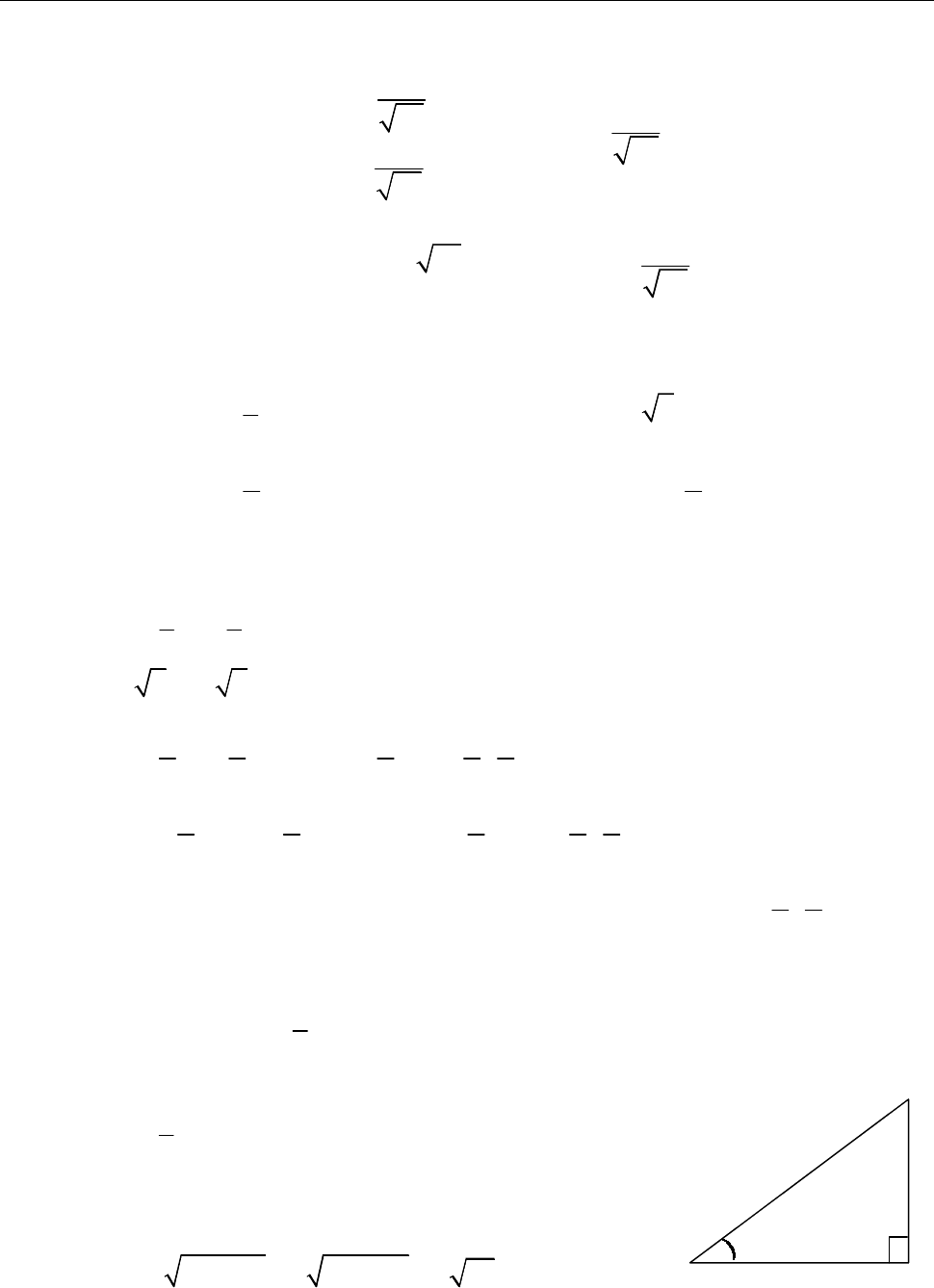
72 Розділ 2. ФУНКЦІЇ
[Крок 3. Визначаємо допоміжний кут із системи.]
1
cos ,
3
10
arcsin .
3
10
sin
10
[Крок 4. Записуємо перетворену формулу.]
3
sin cos 3 10 sin arcsin .
10
x x x
Коментар.
Оскільки
cos 0
та
sin 0,
то кут
лежить у першій чверті.
7.8. Обчислити:
1)
1
sin arcsin ;
3
2)
tg(arctg 2);
3)
arcsin sin ;
8
4)
arctg tg ;
5
5)
arcsin(sin 3);
6)
arccos(cos 4).
Розв’язання.
[2.9.5.]
1.
1 1
sin arcsin .
3 3
2.
tg(arctg 2) 2.
3.
arcsin sin ,
8 8
оскільки
; .
8 2 2
4.
arctg tg ,
5 5
оскільки
; .
5 2 2
5.
arcsin(sin 3) arcsin(sin( 3)) 3,
оскільки
3 ; .
2 2
6.
arccos(cos 4) arccos(cos(2 4)) 2 4,
оскільки
2 4 [0 ].
7.9. Знайти
3
tg arcsin .
5
Розв’язання.
Нехай
3
arcsin .
5
Розглянемо прямокутний трикутник з гіпотенузою
5
c
і катетом
3,
a
який лежить проти кута
.
За Піфагоровою теоремою маємо
2 2 2 2
5 3 16 4.
b c a
Рис. до зад 7.9
3
5
4

7. Тригонометричні функції. Ч. 1 73
Тоді
3
tg .
4
a
b
Задачі для аудиторної і домашньої роботи
7.10. Виразіть у радіанах кут:
1)
20 ;
2)
50 ;
3)
45 ;
4)
60 ;
5)
135 ;
6)
120 ;
7)
240 ;
8)
330 .
7.11. Виразіть у градусах кут:
1)
;
18
2)
;
10
3)
;
4
4)
;
6
5)
2
;
3
6)
3
;
4
7)
7
;
6
8)
5
.
3
7.12. Спростіть вираз:
1)
sin ;
2
t
2)
3
cos ;
2
t
3)
cos(2 );
t
4)
sin( );
t
5)
sin( );
t
6)
cos(2 );
t
7)
cos ;
2
t
8)
3
sin ;
2
t
9)
tg ;
2
t
10)
3
cos ;
2
t
11)
ctg( );
12)
tg( );
13)
sin( ) cos(2 )
;
tg( ) cos( )
t t
t t
14)
sin( ) sin(2 )
.
3
tg( ) cos
2
t t
t t
7.13. Обчисліть за допомогою формул зведення:
1)
5
cos ;
3
2)
7
sin ;
6
3)
11
sin ;
6
4)
7
cos ;
3
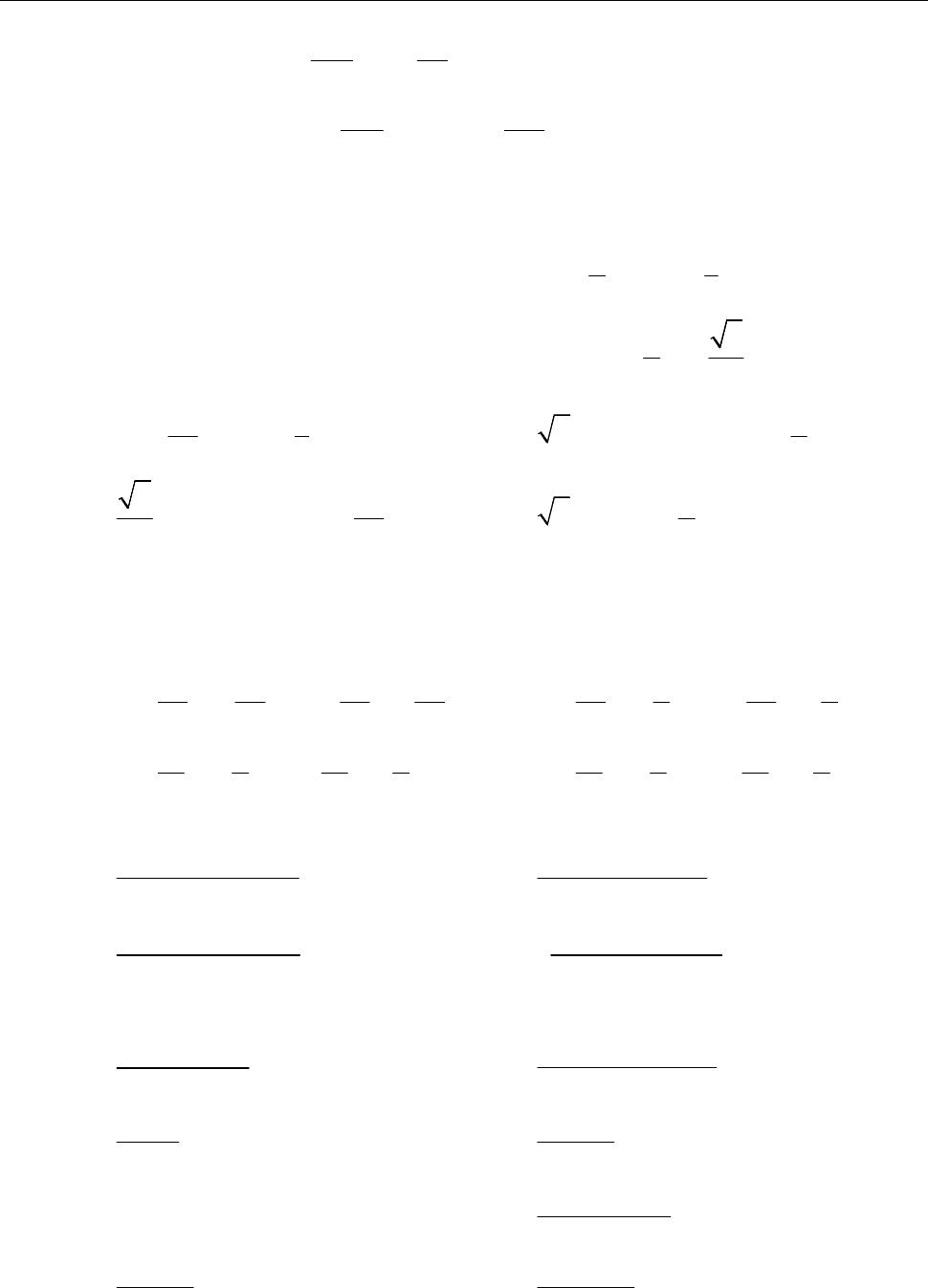
74 Розділ 2. ФУНКЦІЇ
5)
31 7
sin( 7 ) 2 cos tg ;
3 4
6)
49 21
cos( 9 ) 2 sin ctg ;
6 4
7)
sin 75 sin 15 ;
8)
cos105 cos 75 .
7.14. Спростіть:
1)
sin( ) sin cos ;
2)
1
sin sin ;
3 2
3)
sin sin cos( );
4)
2
cos sin ;
4 2
5)
5 1
sin cos ;
6 2
6)
3 cos 2 cos ;
6
7)
3 5
sin cos ;
2 3
8)
2 sin sin ;
4
9)
cos( ) cos cos ;
10)
sin( ) sin( );
11)
sin cos sin( );
12)
cos( ) cos( ).
7.15. Обчисліть:
1)
5 3 5 3
cos cos sin sin ;
8 8 8 8
2)
2 2
sin cos cos sin ;
15 5 15 5
3)
cos cos sin sin ;
12 4 12 4
4)
sin cos cos sin ;
12 4 12 4
5)
sin 77 cos 17 sin 13 cos 73 ;
6)
cos125 cos 5 sin 55 cos 85 ;
7)
tg 25 tg 20
;
1 tg 25 tg 20
8)
tg 9 tg 51
;
1 tg 9 tg 51
9)
1 tg 70 tg 65
;
tg 70 tg 65
10)
1 tg 54 tg 9
.
tg 54 tg 9
7.16. Спростіть:
1)
2
2
2 sin 1
;
1 2 cos
2)
2
(sin cos )
;
1 sin 2
3)
sin 2
sin ;
cos
t
t
t
4)
2
sin 6
;
cos 3
t
t
5)
2
cos cos 2 ;
t t
6)
cos 2
sin ;
cos sin
t
t
t t
7)
sin 40
;
sin 20
8)
sin 100
;
2 cos 50
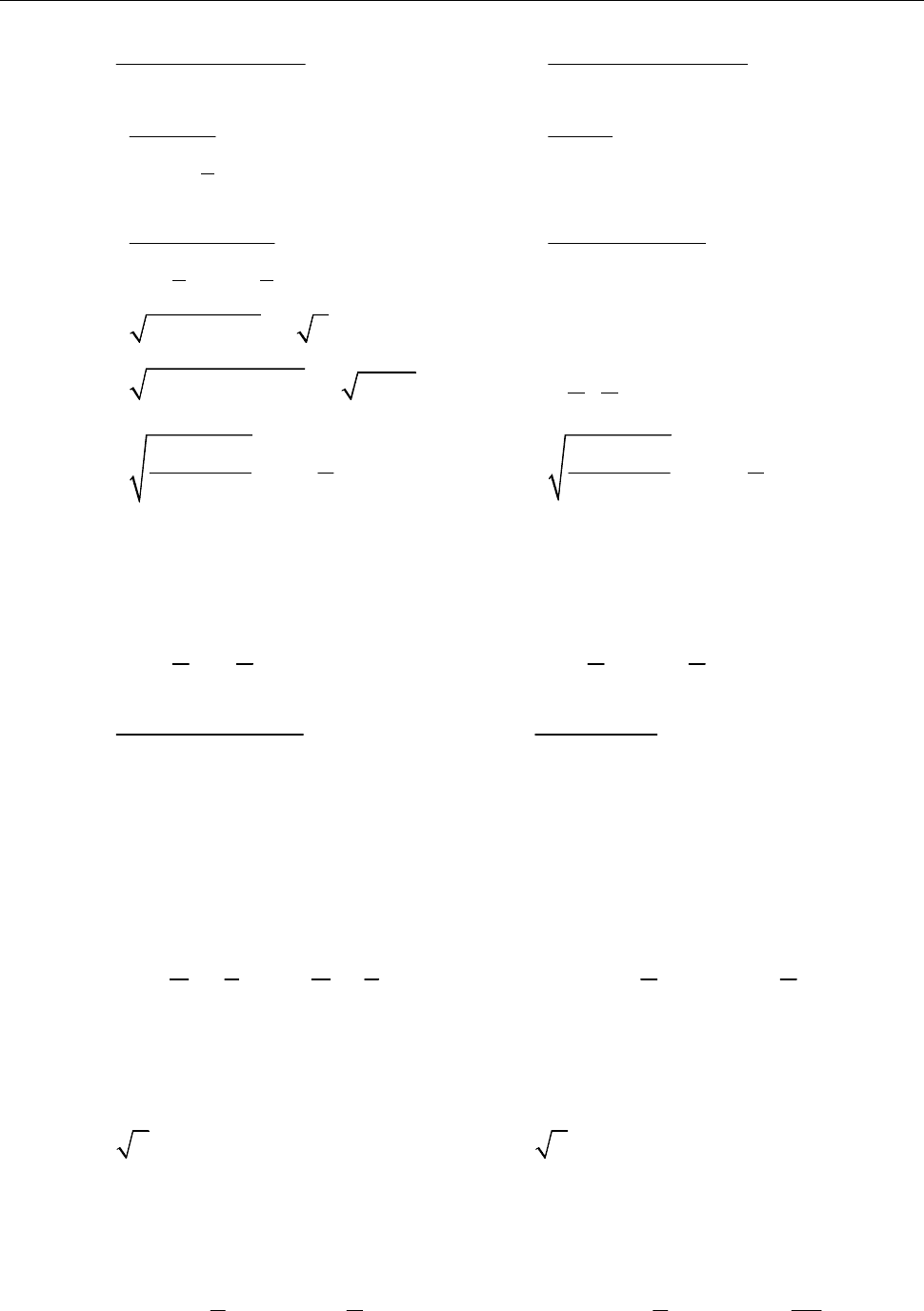
7. Тригонометричні функції. Ч. 1 75
9)
cos 80
;
cos 40 sin 40
10)
2
cos 36 sin 18
;
cos 18
11)
2
sin
;
2 cos
2
t
t
12)
sin 4
;
cos 2
t
t
13)
cos
;
cos sin
2 2
t
t t
14)
cos 2 sin 2
;
cos 4
t t
t
15)
1 cos 2 2 sin , [0; 2 ];
x x x
16)
3
cos cos cos sin , ; ;
2 2
x x x x x
17)
1 cos
tg , ( ; );
1 cos 2
x x
x
x
18)
1 cos
ctg , (0;2 ).
1 cos 2
x x
x
x
7.17. Обчисліть:
1)
2 sin 15 cos 15 ;
2)
2
(cos 75 sin 75 ) ;
3)
2 2
cos 15 sin 15 ;
4)
2
(cos 15 sin 15 ) ;
5)
2 sin cos ;
8 8
6)
2 2
cos sin
8 8
7)
10 sin 40 sin 50
;
cos 10
8)
1 cos 14
tg 7 .
sin 14
7.18. Перетворіть на добуток:
1)
sin 3 sin ;
t t
2)
cos( 2 ) cos( 2 );
3)
cos 6 cos 4 ;
t t
4)
sin( 2 ) sin( 2 ).
7.19. Перетворіть на суму:
1)
sin( ) sin( );
2)
cos( ) cos( );
3)
cos cos ;
2 2 2 2
4)
cos cos ;
4 4
5)
sin cos( );
6)
cos sin( ).
7.20. Перетворіть вираз до вигляду
sin( ), 0
A t A
:
1)
sin 5 cos 5 ;
x x
2)
cos 4 sin 4 ;
x x
3)
3 sin cos ;
x x
4)
3 sin cos ;
x x
5)
12 cos 5 sin ;
x x
6)
4 sin 3 cos ;
x x
7)
sin cos ;
x x
8)
7 sin 24 cos .
x x
7.21. Знайдіть значення інших тригонометричних функцій кута
,
якщо:
1)
1
sin , 0 ;
3 2
2)
1 3
sin , ;
8 2
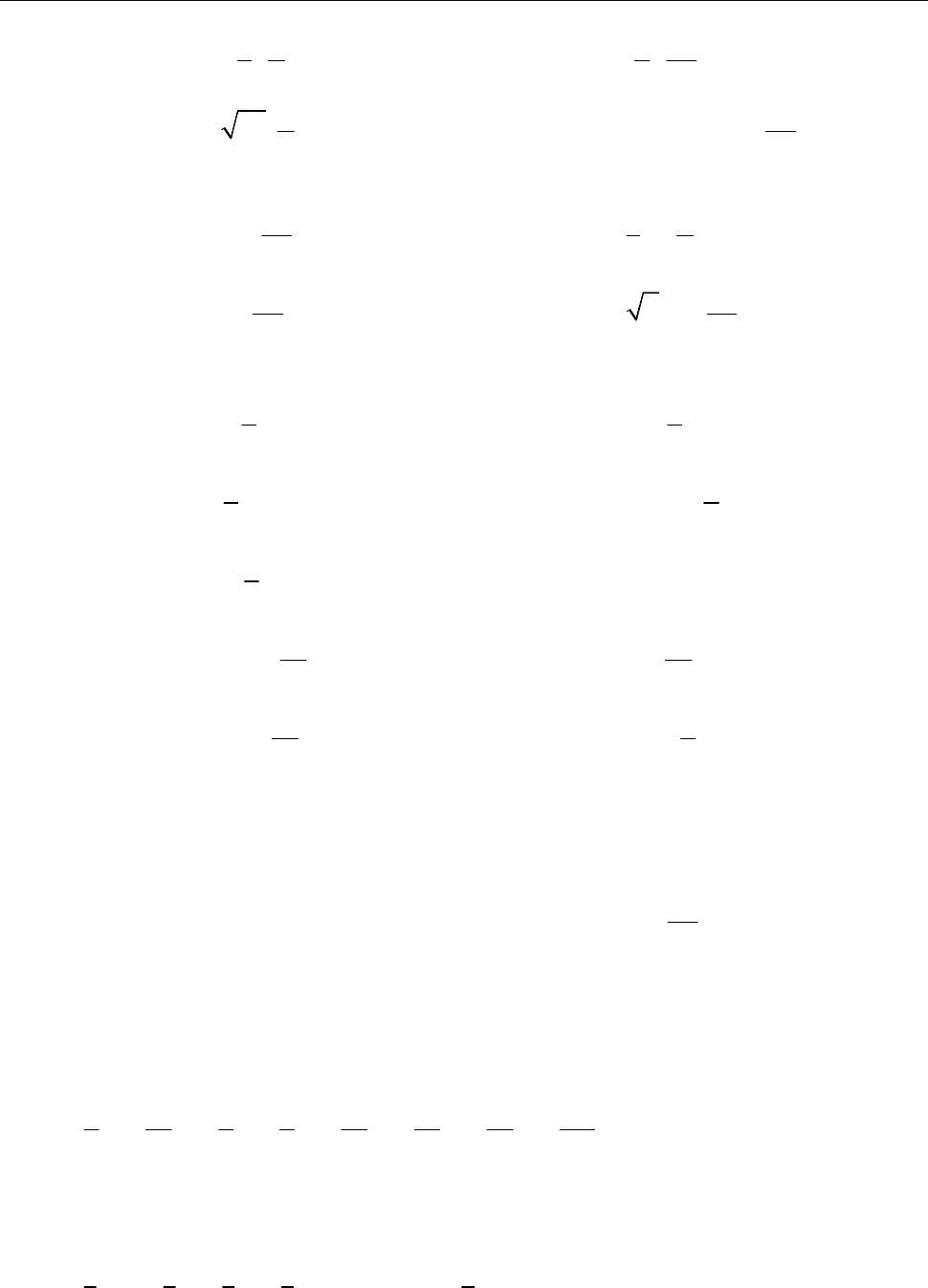
76 Розділ 2. ФУНКЦІЇ
3)
2
cos , ;
5 2
4)
4 3
cos , 2 ;
5 2
5)
tg 15, ;
2
6)
3
ctg 3, .
2
7.22. Обчисліть:
1)
2
arcsin 2 cos ;
3
2)
1
arccos tg ;
2 3
3)
7
arctg 2 cos ;
6
4)
2
arcctg 3 ctg .
3
7.23. Обчисліть:
1)
2
sin arcsin ;
5
2)
1
cos arccos ;
5
3)
1
tg arctg ;
3
4)
1
ctg arcctg ;
4
5)
3
sin arccos ;
5
6)
sin(arccos( 0, 8));
7)
5
cos arcsin ;
13
8)
8
cos arcsin ;
17
9)
5
tg arccos ;
13
10)
4
ctg arccos ;
5
11)
tg(arcsin 0, 6);
12)
ctg(arcsin( 0, 8)).
7.24. Обчисліть:
1)
arcsin(sin 1, 2 );
2)
arccos(cos 1, 3 );
3)
arctg tg 3, 3 ;
4)
3
arcctg ctg ;
5
5)
arcsin sin 6;
6)
arcsin sin 22;
7)
arccos cos 11;
8)
arccos cos 34.
Відповіді
7.10. 1)
;
9
2)
5
;
18
3)
;
4
4)
;
3
5)
3
;
4
6)
2
;
3
7)
4
;
3
8)
11
.
6
7.11. 1)
10 ;
2)
18 ;
3)
45 ;
4)
30 ;
5)
120 ;
6)
135 ;
7)
210 ;
8)
300 .
7.12. 1)
cos ;
t
2)
sin ;
t
3)
cos ;
t
4)
sin ;
t
5)
sin ;
t
6)
cos ;
t
7)
sin ;
t
8)
cos ;
t
9)
ctg ;
t
10)
sin ;
t
11)
ctg ;
12)
tg ;
13)
cos ;
t
14)
cos .
t
7.13. 1)
1
;
2
2)
1
;
2
3)
1
;
2
4)
1
;
2
5)
2;
6)
1;
7)
1
;
4
8)
0.
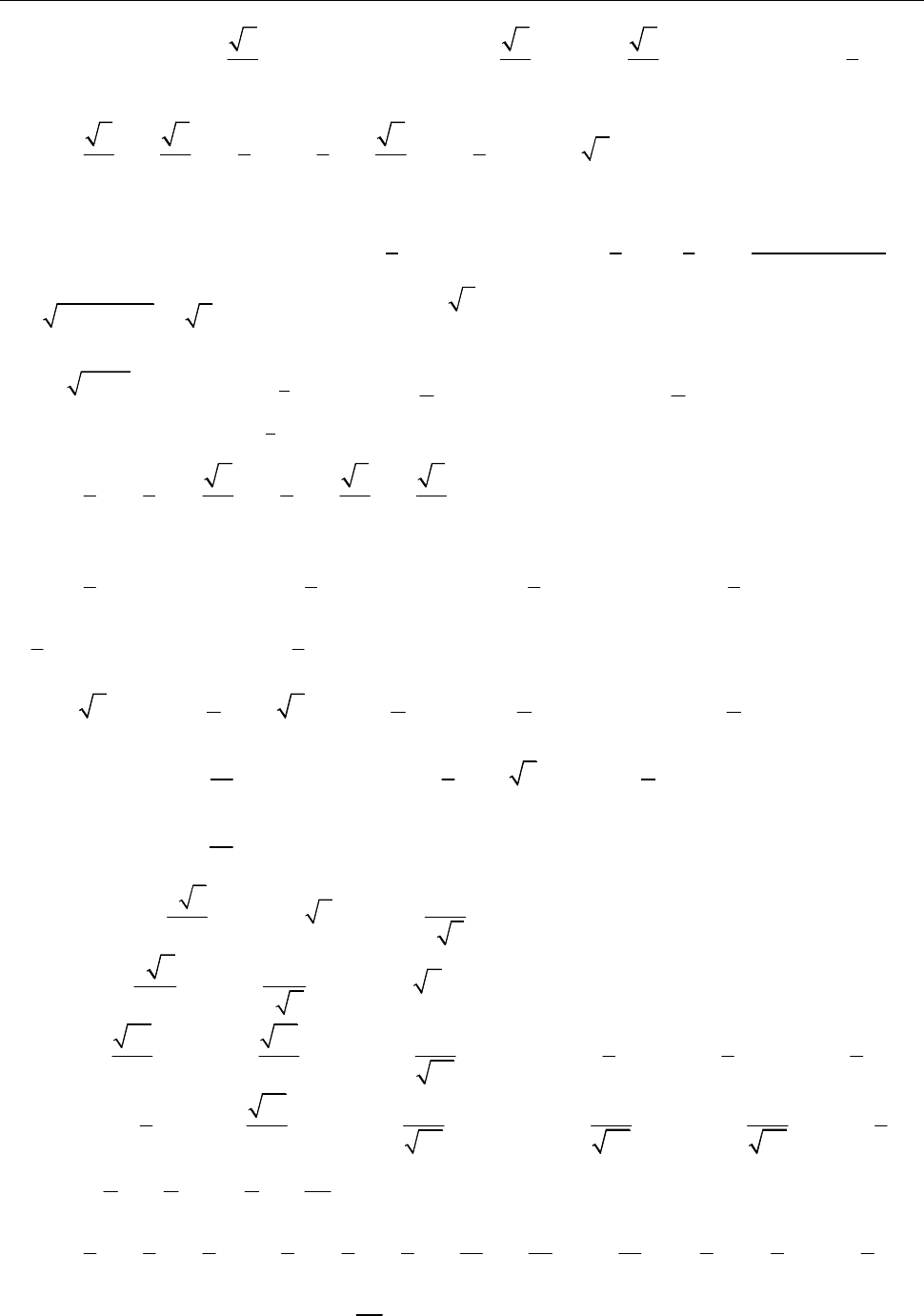
7. Тригонометричні функції. Ч. 1 77
7.14. 1)
sin cos ;
2)
3
cos ;
2
3)
cos cos ;
4)
2
cos ;
2
5)
3
sin ;
2
6)
sin ;
7)
1
cos ;
2
8)
cos ;
9)
sin sin ;
10)
2 sin cos ;
11)
sin cos ;
12)
2 cos cos .
7.15. 1)
2
;
2
2)
3
;
2
3)
1
;
2
4)
1
;
2
5)
3
;
2
6)
1
;
2
7)
1;
8)
3;
9)
1;
10)
1.
7.16. 1)
1;
2)
1;
3)
sin ;
t
4)
2 tg 3 ;
t
5)
2
sin ;
t
6)
cos ;
t
7)
2 cos 20 ;
8)
2 sin 50 ;
9)
cos 40 sin 40 ;
10)
cos18 ;
11)
tg ;
2
t
12)
2 sin 2 ;
t
13)
cos sin ;
2 2
t t
14)
1
.
cos 2 sin 2
t t
15)
1 cos 2 2 sin , [0; 2 ];
x x x
16)
2 2 sin , [0; ],
0, [ ;2 ];
x x
x
17)
2
2
2 cos sin , 0; ,
0, ; 0 ;
x x x
x
18)
2 tg , [0; ),
2
0, ( ; 0];
x
x
x
19)
2 ctg , (0; ],
2
0, [ ;2 ).
x
x
x
7.17. 1)
1
;
2
2)
1
;
2
3)
3
;
2
4)
3
;
2
5)
2
;
2
6)
2
;
2
7)
5 tg 40 ;
8)
1.
7.18. 1)
2 cos 2 sin ;
t t
2)
2 sin sin 2 ;
3)
2 cos cos 5 ;
t t
4)
2 cos sin 2 ;
7.19. 1)
1
(cos 2 cos 2 );
2
2)
1
(cos 2 cos 2 );
2
3)
1
(cos cos );
2
4)
1
cos 2 ;
2
5)
1
(sin( 2 ) sin );
2
6)
1
(sin(2 ) sin ).
2
7.20. 1)
2 sin 5 ;
4
x
2)
2 4 ;
4
x
3)
2 sin ;
3
x
4)
2 sin ;
6
x
5)
12
13 sin arctg ;
5
x
6)
3
5 sin arctg ;
4
x
7)
2 sin ;
4
x
8)
24
25 sin arctg .
7
x
7.21. 1)
2 2 1
cos , tg 2 2, ctg ;
3
2 2
2)
3 7 1
cos , tg , ctg 3 7;
8
3 7
3)
21 21 2
sin , tg , ctg ;
5 2
21
4)
3 3 4
sin , tg , ctg ;
5 4 3
5)
1 15 1
cos , sin , ctg ;
4 4
15
6)
1 3 1
sin , cos , tg .
3
10 10
7.22. 1)
;
2
2)
;
6
3)
;
3
4)
3
.
4
7.23. 1)
2
;
5
2)
1
;
5
3)
1
;
3
4)
1
;
4
5)
4
;
5
6)
3
;
5
7)
12
;
13
8)
15
;
17
9)
12
;
5
10)
4
;
3
11)
3
;
4
12)
3
.
4
7.24. 1)
0,2 ;
2)
0, 7 ;
3)
0, 3 ;
4)
3
;
5
5)
6 2 ;
6)
7 22;
7)
4 11;
8)
34 10 .

78 Розділ 2. ФУНКЦІЇ
8. Тригонометричні функції. Ч. 2
Навчальні задачі
8.1.1. Розв’язати рівняння
3
sin .
2
x
Розв’язання.
[2.14.3.]
3 3
sin ( 1) arcsin ( 1) , .
2 2 3
n n
x x n n n
( 1) , .
3
n
x n n
8.1.2. Розв’язати рівняння
1
sin .
3
x
Розв’язання.
[2.14.3.]
1
1 1 1
sin ( 1) arcsin ( 1) arcsin , .
3 3 3
n n
x x n n n
1
1
( 1) arcsin , .
3
n
x n n
8.1.3. Розв’язати рівняння
sin 2 0.
4
x
Розв’язання.
[2.14.3.]
sin 2 0 2 2 , .
4 4 4 8 2
n
x x n x n x n
, .
8 2
n
x n
8.2.1. Розв’язати рівняння
2
cos .
2
x
Розв’язання.
[2.14.4.]
2 2
cos arccos 2
2 2
2
arccos 2 2
2 4
3
2 , .
4
x x n
x n x n
x n n
3
2 , .
4
x n n
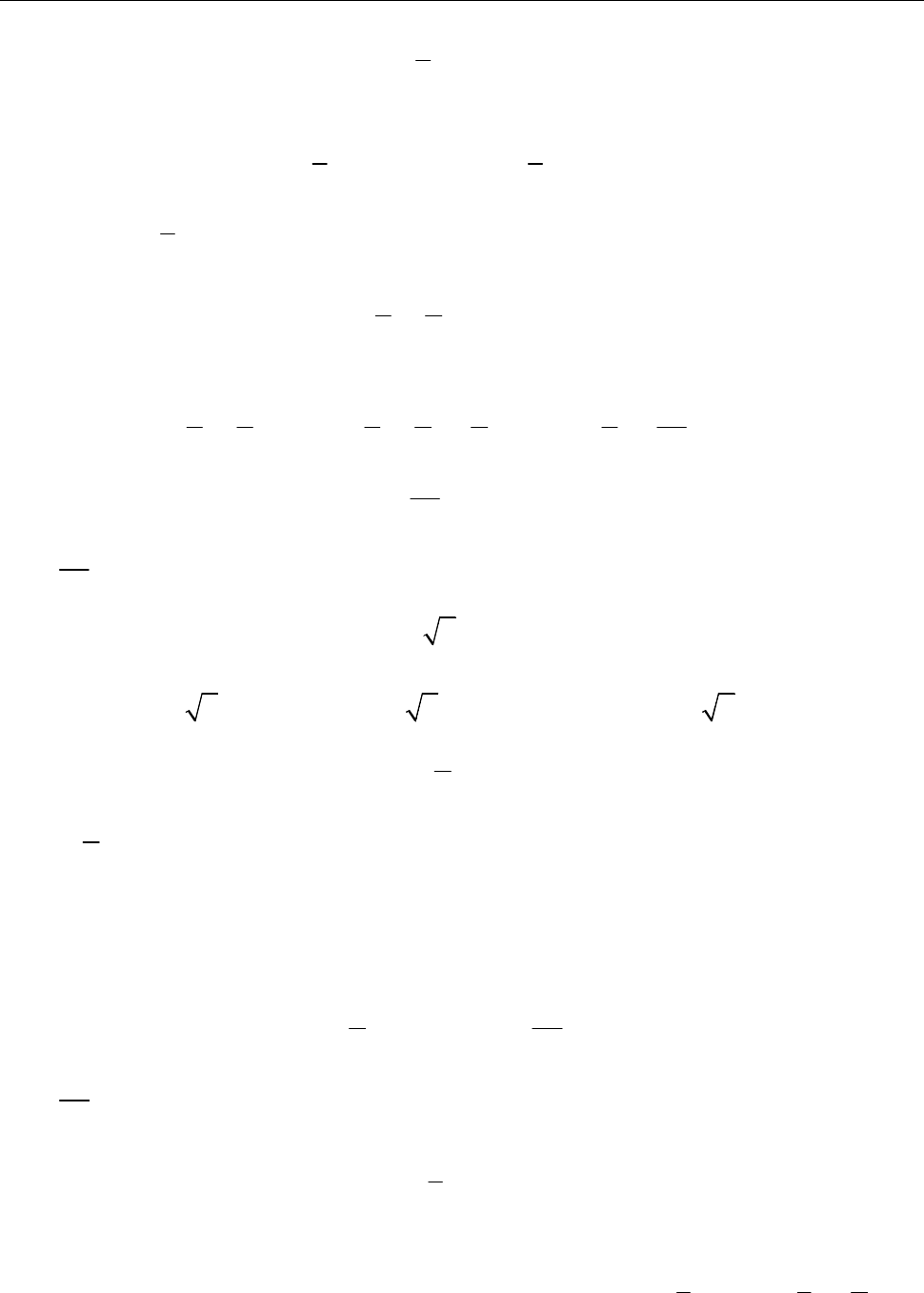
8. Тригонометричні функції. Ч. 2 79
8.2.2. Розв’язати рівняння
1
cos .
3
x
Розв’язання.
[2.14.4.]
1 1
cos arccos 2 , .
3 3
x x n n
1
arccos 2 , .
3
x n n
8.2.3. Розв’язати рівняння
cos 0.
2 3
x
Розв’язання.
[2.14.4.]
5
cos 0
2 3 2 3 2 2 6
5
2 , .
3
x x x
n n
x n n
5
2 , .
3
x n n
8.3. Розв’язати рівняння
tg 3.
x
Розв’язання.
[2.14.5.]
tg 3 arctg( 3) arctg 3
, .
3
x x n x n
x n n
, .
3
x n n
8.4. Розв’язати рівняння
ctg 1.
x
Розв’язання.
[2.14.6.]
ctg 1 arcctg( 1) arcctg 1
3
, .
4 4
x x n x n
x n x n n
3
, .
4
x n n
8.5. Розв’язати нерівність
1
sin .
2
x
Розв’язання.
[2.14.3.]
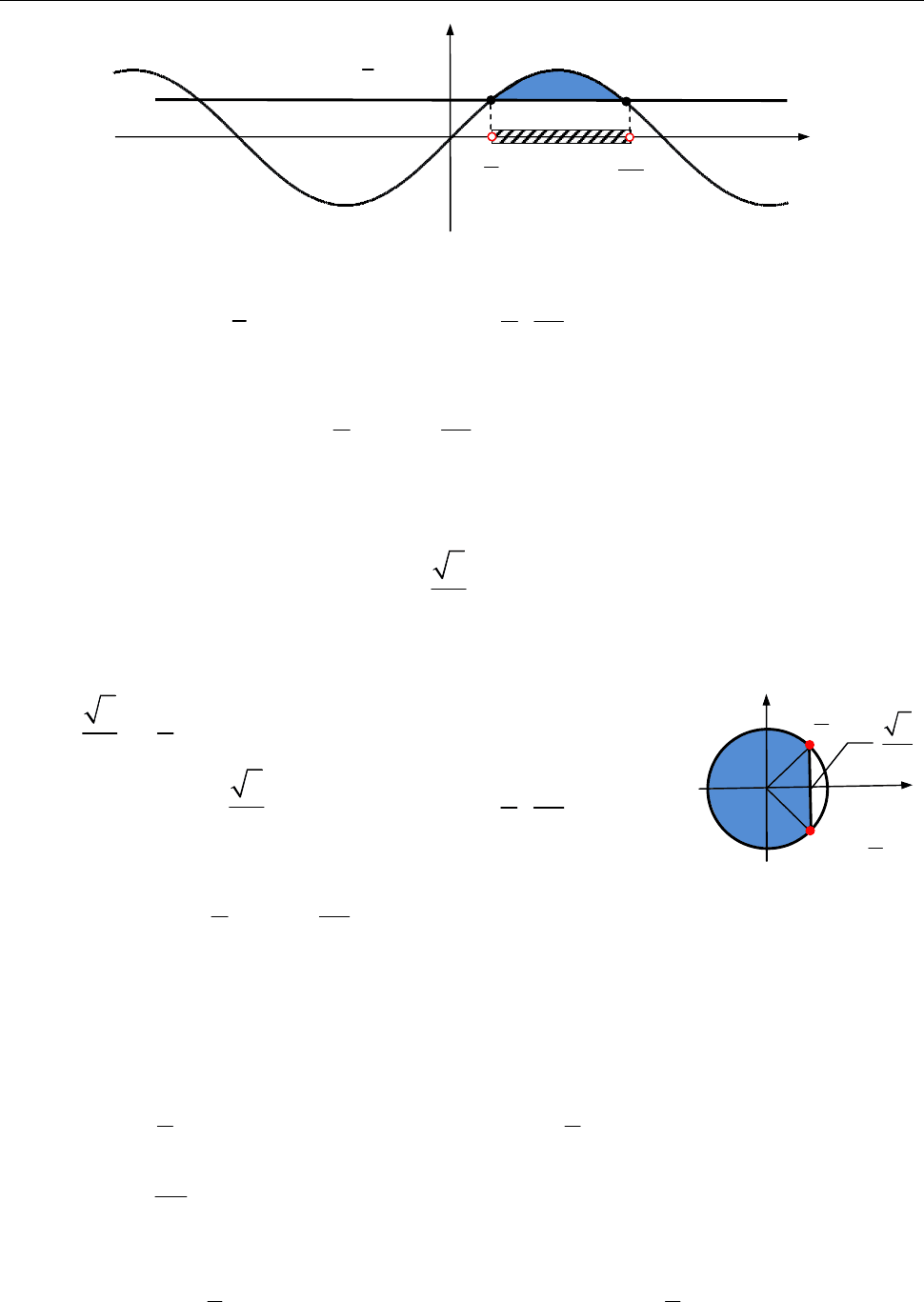
[Розв’язуємо нерівність, будуючи графіки
sin
y x
і
1
.
2
y
]
1
arcsin .
2 6
80 Розділ 2. ФУНКЦІЇ
Рис. до зад 8.5
Нерівність
1
sin
2
x
правдива для
; .
6 6
x
Ураховуючи періодичність
синуса, маємо
5
2 ; 2 , .
6 6
x n n n
Коментар.
Задачу можна розв’язати за допомогою графіка
sin
y x
або на
одиничному колі.
8.6. Розв’язати нерівність
2
cos .
2
x
Розв’язання.
[2.14.4.]
[Розв’язуємо нерівність за допомогою одиничного кола.]
2
arccos .
2 4
Нерівність
2
cos
2
x
правдива для
7
; .
4 4
x
Урахо-
вуючи періодичність косинуса, маємо
7
2 ; 2 , .
4 4
x n n n
Рис. до зад 8.6
Задачі для аудиторної і домашньої роботи
8.7. Розв’яжіть рівняння:
1)
sin 3 0;
x
2)
ctg 7 0;
x
3)
cos 0;
4
x
4)
tg 0;
5
x
5)
sin 1;
2
x
6)
sin 4 1;
x
7)
cos 2 1;
x
8)
cos 5 1;
x
9)
1
sin ;
3
x
10)
1
cos ;
3
x
y
x
2
2
4
2
4
1
y
x
sin
y x
6
5
6
1
2
y
O
